一种基于FTS车削的微切削力模型
谢晓麟,周晓勤,张新,张继真,谭双龙
(1.中国科学院长春光学精密机械与物理研究所 中国科学院光学系统先进制造技术重点实验室,长春 130033;2.吉林大学 机械科学与工程学院,长春 130022)
一种基于FTS车削的微切削力模型
谢晓麟1,周晓勤2,张新1,张继真1,谭双龙1
(1.中国科学院长春光学精密机械与物理研究所 中国科学院光学系统先进制造技术重点实验室,长春 130033;2.吉林大学 机械科学与工程学院,长春 130022)
机械加工中的切削力模型建立对于研究工件表面形貌成型,探究切削理论有着深远的意义。在微切削加工领域,伺服车削通常用来加工自由曲面,但是考虑到尺寸效应,传统宏观领域的切削力模型无法真实地描述切削过程。针对微切削加工领域,提出了一种切削力模型,模型充分考虑了最小未成型切屑厚度,刀具切削刃钝圆以及工件对后刀面回弹引起的摩擦力。由于切削深度不同,所对应的切削原理也不同,将切削过程分为多个区域建模。当刀具切入工件后,随着切屑厚度的减小,切屑在前刀面分别经历宏观剪切、大负前角切削以及耕梨过程,而同时工件未切下的部分在后刀面的进一步作用下形成已加工表面,对应上述过程,将分为4个区域建模。最后,基于自主设计的能够精确测量两个方向切削力的快刀伺服装置(DFT-FTS)设计实验。
微切削力模型;快速刀具伺服;尺寸效应;自由曲面
对于机械加工,切削力是一个十分重要的参数。一直以来,切削力被认为与工件表面形貌成型的加工过程直接相关。加工表面形貌的优劣通常以粗糙度、毛刺以及面型误差等作为判断标准,伴随着加工尺度越来越精细化,前两者逐渐成为关键因素[1]。由于传统模型是建立在剪切理论的基础上,难以捕捉到上述两个因素。因此,近年来建立能够应用在微切削领域的切削力模型成为研究切削理论的焦点[2]。
Zvorykin等人奠基了传统领域的切削力模型,后来经由Ernst、Merchant的研究,发展成为单剪切力平面模型,这些模型都是在宏观尺度下进行探索,关注焦点是如何推导剪切角,其中一个较为有效的方法就是最小能量法。Lee和Shafer后来创新性地基于工程塑性力学分析金属切削过程,推动切削理论产生新的发展。20世纪末,Dewhurst依据塑性理论建立滑移线场,分析金属切削过程中工件的塑性变形,构造出滑移线切削模型。对于切削模型建立具有指导意义,对于切削理论的研究产生深远影响,为解析型切削模型奠定了基础。
但是,微尺度切削过程均无法通过上述模型直接描述,宏观刀尖形状如图1所示。由于“尺寸效应”,微尺度切削过程切屑厚度极小,与刀尖切削刃钝圆半径数量级相当,如图2所示,使得刀具进行大负前角切削,工件弹塑性变形并重[3]。切削力、切屑成型和厚度、加工表面成型质量等都受到尺寸效应的影响[4]。因此,刀尖切削刃钝圆半径成为微尺度下的关键,同时不能忽略最小未成型切屑厚度(MUCT)3,5-7]。在刀尖切削刃钝圆圆周上对应MUCT的点被称为“中性点”(neutral point)或“滞点”(stagnation point)。当背吃刀量小于MUCT时,切削过程主要体现为耕梨效应,而当背吃刀量大于MUCT,大负前角切削占主导。

图1 宏观刀尖形状

图2 微切削尺度下刀尖形状
对于微切削加工,耕梨力是切削力构成重要的部分之一。但是耕梨力模型该如何建立学者们还有很多争议。现有两种主要方法:滑移线理论模型[8-11],如图 3 和基于压印效应的积分模型[3,12,13],如图4所示。
实际加工过程中,很多研究者注意到,刀尖切削刃钝圆圆周前端会形成工件材料的堆积,类似于传统领域切削的积屑瘤。因此,通过滑移线理论建立耕梨力模型通常基于如下假设,刀尖刃钝圆处始终被工件材料形成一个三角形无限尖的堆积,并可视为“刀尖”,实际加工过程是以这个堆积刀尖在实现真正的切削。上述假设回避了刀尖刃钝圆,认为工件材料在加工过程被钝圆处堆积上的刀尖切割分流[7]。因此,直接应用传统领域宏观尺度下切削力模型,不需要积分。

图3 滑移线理论模型和
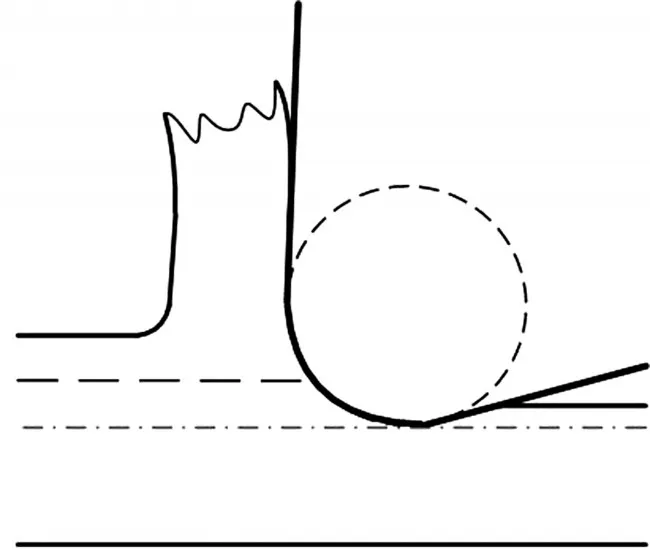
图4 基于压印效应的积分模型
而其他研究者认为,切屑直接与刀尖刃钝圆发生作用,工件材料从滞点处切割分流,滞点以上的材料形成切屑流向前刀面,滞点以下的材料,在耕梨力的作用下流向后刀面,同时受到后刀面的挤压发生弾塑性变形,最终形成工件表面。因此,耕梨力建模必须要包含挤压作用,从而形成了基于压印效应的模型[3],其中切削力的分布沿着刀尖刃钝圆圆周,需要通过积分运算进行模型。
考虑MUCT时,不同切削深度对应的切削原理不同,切削力由于性质不同易产生分类混乱。这种混乱对自由曲面微切削原理的研究影响更为严重。切削深度随着自由曲面加工过程始终在变化,因此,针对不同切削深度进行建模尤为重要。近年来,随着加工尺度精细化,微切削领域的相关研究越来越受到关注[14]。本文提出了如下微切削力模型。该预测模型对上述混乱进行了梳理,并同时将后刀面的影响也包含其中。
1 切削力模型
在切削过程中,刀具不同位置与工件接触时会展现出不同的力学特性,因此,比较合理的切削力建模方法是分区处理。如Altintas[15]提出的切削力模型:

其中,Kte与Kfe表示刃口力系数,Ktc与Kfc表示切削力系数,b是切削宽度,h是切削深度。本文根据对应于不同切深的不同切削力特性进行系统明确的分区,如图5所示。

图5 切削力建模分区图
工件材料在滞点处被刀具分割,流向两个方向。区域1和区域2处的材料流向前刀面,最终形成切屑,区域3和区域4处的材料流向后刀面,最终构成被加工表面。滞点可以等效于宏观尺度切削中刀尖点。那么,刀具轮廓上位于滞点之上的部分,即钝圆圆弧以上部分,在微切削尺度成为实际前刀面,见图3粗虚线。刀具轮廓上位于滞点之下的部分,即钝圆圆弧以下部分,可以作为实际后刀面,见图3粗实线。综合各区之和建立总的切削力模型。下面以切向力为例,基于正交切削条件,建立解析模型。
1.1 区域1(Region 1)模型
区域1的切削过程由前刀面部分完成,刀具钝圆并没有参与,除去分区后切削载荷的作用面积不同外,其他参数均未变,直接采用传统宏观尺度切削力模型进行计算。本文采用Merchant[16]的方法建立切削力模型:

其中,h>hc=(1+sinαr)re,τs表示工件材料屈服剪切应力,ϕc表示剪切角,βa表示摩擦角,αr表示刀具前角,hc表示前刀面与钝圆弧相接点到刀具底部的垂直距离,如图6所示。

图6 作用于区域1前刀面的切向切削力
1.2 区域2(Region 2)模型
区域2的切削过程由切削刃钝圆弧滞点之上的部分完成,工作部分的每点的实际前角都不相同,随着MUCT的减小,实际前角逐渐向大负前角过渡,如图7所示。

图7 作用于区域2钝圆弧上的切向切削力
每个未成型切屑厚度都对应着钝圆的某个圆心角,根据几何关系可得:

通过区域2对应的未成型切削厚度MUCT范围能够推到出角度变化范围:

区域2钝圆弧上某点的切削面积可表达为:

则区域2钝圆弧上某点的切向力可表达为:

当θm<θ≤θc时,由几何关系有将其带入上式可得到:
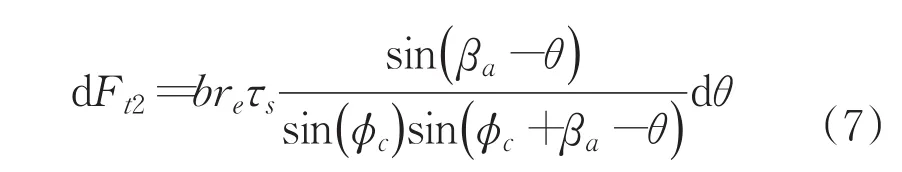
在整个区域2上对圆弧积分得出切向力:

1.3 区域3(Region 3)模型
区域3的切削深度小于MUCT,并没有产生实际切屑,只是工件表面被耕梨的过程。由切削刃钝圆弧滞点之下的部分完成。在耕梨过程中,值得注意的是,并不是只有沿钝圆圆弧的切向力作用,同时还有沿圆弧径向的挤压力作用在工件表面。挤压作用使得工件材料产生弾塑性变形,对工件表面产生严重影响,如图8所示。

图8 作用于区域3钝圆弧上的切向耕梨力
因此,区域3钝圆弧上某点耕梨力的切向分力可表达为如下两部分:

其中,k表示弾塑性变形的切削参数,单位为pa,为粘性阻尼系数。通过区域3切削深度得出相对应的圆心角范围:

在整个区域3上积分得出耕梨力的切向分力为:

1.4 区域4(Region 4)模型
后刀面会抑制工件回弹变形,因而产生力的作用。后刀面对工件表面的作用,对于加工表面粗糙度以及残余应力等都产生重要影响。因此在建立模型时需要充分考虑其影响[15,17],尤其对于负后角切削建模更为关键[19,20]。
在考虑后刀面的影响时,一些学者将后刀面与钝圆耕梨区域联合处理[17]。另一些学者则在分析复合材料纤维方向同时,对后刀面部分切削力建模[19]。本文依据材料回弹特性建模。当工件材料经过刀尖钝圆弧最低点后,会发生回弹变形。由于后刀面限制,回弹力将垂直的作用于后刀面上,并沿后刀面切向产生摩擦力,如图9所示。
由胡克定律,后刀面上某点的回弹力可表达为:

后刀面上某点与工件表面接触产生摩擦力,表达如下:

则可得到后刀面上某点的切向切削力力,如下:

其中,k表示工件弹性系数,αc表示刀具后角。
对整个区域4进行积分得到切向力:


图9 作用于区域4上的切向切削力力
1.5 综合切削力模型
将各区切削力综合起来,则总的切向切削力可表达为:

根据切削深度的变化,可以简化如下:

MUCT所对应的钝圆圆心角的值取摩擦角βα[3],带入到上式中可得到更加简化的形式,在此不再赘述。通过模型可以发现,除了耕梨过程,一旦切削深度增加到一定程度,微切削力将与切深呈现同种趋势变化。在耕梨过程中,切削力则与切深呈现相反的趋势,与“尺寸效应”现象相符合。
2 切削实验
本文切削实验基于德国Spinner SB/C TMC精密机床进行,该机床的超精密液压主轴能够实现微尺度级别的切削,如图10所示。
如图11所示,为自主设计的DFT-FTS,将其安装在机床溜板上,可随溜板实现沿机床x轴和z轴进给运动。加工工件时,溜板沿x轴产生恒定进给运动,同时快刀伺服系统由压电驱动源沿z轴输出高频运动,从而加工工件周向形貌。采用人工合成金刚石(PCD)作为刀具刀尖材料,刀具半径1mm,理论刀尖切削刃钝圆半径为200nm,前角0°,后角20°。本文设计两种切削试验,分别为了平面切削和自由曲面切削,切削工件均为铝材。

图10 Spinner SB/C TMC精密机床

图11 能够同时实现两向切削力精确测量的快刀伺服装置(DFT-FTS)
平面切削,设置机床主轴转速400r/min,每转溜板沿x轴的进给量10μm,通过控制机床z轴进给量使切削深度分别为100μm和20μm,记录60s内的切削过程,得到的力信号见图12和图13。

图12 切深为100μm平面切削时切削力测量值

图13 切深为20μm平面切削时切削力测量值
自由曲面切削,系统开环,由信号发生器对压电驱动器提供正弦激励信号。机床主轴转速为同样设置为400r/min,主轴每转溜板沿x轴进给10μm,沿z轴进给50μm,通过机床沿z轴产生进给和快刀伺服装置的压电驱动,叠加形成刀具切削深度。在信号发生器输出低频正弦激励时,60s内测得的力信号及切深分别如图14和图15所示。
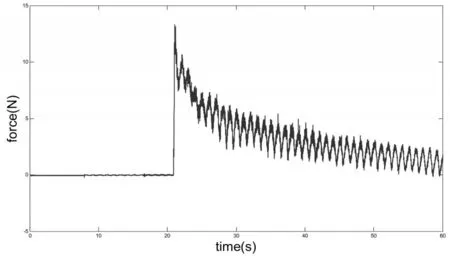
图14 低频正弦激励下测得的力信号

图15 低频正弦激励下测得的切削深度
显微镜下所加工表面形貌如图16所示。

图16 显微镜下加工表面的形貌
微切削过程,切削量为几个或十几个微米情况下,切削力大体变化范围为几牛数量级,由于刀具刃口磨损会造成微进给时与工件表面接触不良,为了避免上述情况,突出切削力的值,本文同时设置溜板输出较大的切深进给。通过途中切削力的曲线可以看出,溜板切入大进给量的瞬间,切削力也出现很大的瞬态变化,直到溜板进给稳定后,切削力值才出现规律变化。随着刀具沿x轴方向进给运动,主轴转速不变情况下,等效切削速度在减小,从而切削载荷变小,切削力也呈现逐渐减小的总体趋势。
通过本文建立的切削力模型可以发现,当切深增加,实际切屑厚度大于最小未成型切屑厚度时,切削力与切削深度同趋势变化,而当切削发生在耕梨区内,切屑难以成型,这时切削力会与切深呈现相反趋势变化。
3 结论
本文提出了一种切削力模型,将刀尖切削刃钝圆和刀具后刀面对加工表面的挤压作用都考虑其中,针对不同切深对应不同切削原理进行了分区建模,通过综合模型描述切削力。
为了实现微切削力在线测量,研制了一种能够同时测量两方向切削力的快刀伺服装置(DFTFTS),进行了实际加工过程中的切削力测量试验,通过平面切削和自由曲面切削对模型进行验证。
当刀具切入后,切削状态稳定后,切削力与实际切深的关系与预测模型基本相符,切削力与切深呈现同种趋势变化。但由于切入过程太快,外界噪声等影响,对考虑刀具切削刃钝圆的影响还需要进一步验证。
[1]Aramcharoen A,Mativenga P T.Size effect and tool geometry in micromilling of tool steel[J].Precision Engineering,2009,33(4):402-407.
[2]谢晓麟.自由曲面伺服车削切削力测量及装置研制[D].长春:吉林大学,2015.
[3]Malekian M,Mostofa M G,Park S S,et al.Modeling of minimum uncut chip thickness in micro machining of aluminum[J].Journal of Materials Processing Technology,2012,212(3):553-559.
[4]Liu X,Devor RE,Kapoor SG,et al.The mechanics of machining at the microscale:assessment of the current state of the science[J].Journal of Manufacturing Science&Engineering,2004,126(4):5064-5070.
[5]Basuray P K,Misra B K,Lal G K.Transition from ploughing to cutting during machining with blunt tools.[J]Wear,1977,43(3):341-349.
[6]Yuan Z J,Zhou M,Dong S.Effect of diamond tool sharpness on minimum cutting thickness and cutting surface integrity in ultraprecision machining[J].Journal of Materials Processing Technology,1996,62(4):327-330.
[7]Kim C J,Bono M,Ni J.Experimental analysis of chip formation in micro-milling[J].NAMRI issue,2002,159(2):1-8.
[8]Waldorf D J,Devor R E,Kapoor S G.A slip-line field for ploughing during orthogonal cutting[J].Journal of Manufacturing Science&Engineering,1998,120(4):693-699.
[9]Waldorf D J,DeVor R E,Kapoor S G.An evaluation of ploughing models for orthogonal machining[J].Journal of Manufacturing Science&Engineering,1999,121(4):550-558.
[10]Waldorf D J.A simplified model for ploughing forces in turning[J].Journal of Manufacturing Processes,2006,8(8):76-82.
[11]Pramanik A,Zhang L C,Arsecularatne J A.Prediction of cutting forces in machining of metal matrix composites[J].International Journal of Machine Tools&Manufacture,2006,46(14):1795-1803.
[12]Hyung Wook Park,Steven Y Liang.Force modeling of micro-grinding incorporating crystallographic effects[J].International Journal of Machine Tools&Manuacture,2008,48(15):1658-1667.
[13]Asma Perveen,Rahman M,Wong Y S.Modeling and simulationofcuttingforcesgeneratedduring vertical micro-grinding[J].The International Journal of AdvancedManufacture,2014,71(9):1539-1548.
[14]于占江,张超楠,王雯.表面沟槽微织构刀具高速微车削试验研究[J].长春理工大学学报:自然科学版,2015,38(03):72-76.
[15]Altintas Y.Manufacturing automation:metal cutting mechanics,machine tool vibrations,and CNC design[M].Cambridge:Cambridge University Press,March 2000:20-40.
[16]Merchant M E.Mechanics of the metal cutting process.I.Orthogonal cutting and type 2 chip[J].Journal of Applied Physics,1945,16(5):267-275.
[17]Park S S,Malekian M.Mechanistic modeling and accurate measurement of micro end milling forces[J].CIRP Annals-Manufacturing Technology,2009,58(1):49-52.
[18]Zhang L C.Cutting composites:A discussion on mechanics modeling[J].Journal of Materials Processing Tech,2009,209(9):4548-4552.
[19]Transchel R,Leinenbach C,Wegener K.Cutting and ploughing forces for small clearance angles of hexaoctahedron shaped diamond grains[J].CIRP Annals-Manufacturing Technology,2014,63(1):325-328.
[20]李晓舟,于化东,许金凯,等.微切削加工中切削力的理论与实验[J].光学精密工程,2009,17(5):1086-1092.
A Micro Cutting Force Model Based on FTS Turning
XIE Xiaolin1,ZHOU Xiaoqin2,ZHANG Xin1,ZHANG Jizhen1,TAN Shuanglong1
(1.Changchun Institute of Optics,Fine Mechanics and Physics,Chinese Academy of Science,Key Laboratory of Optical System Advanced Manufacturing Technology,Chinese Academy of Sciences,Changchun 130033;2.School of Mechanical Science and Engineering,Jilin University,Changchun 130022)
The establishment of cutting force model in machining is of great significance to study the surface morphology of workpiece and explore the cutting theory.Due to the so-called size effect,the cutting force model in the traditional field can not be directly applied to the micro-machining of free-form surface servo turning.In this paper,a cutting force prediction model for micro-cutting is proposed.The model gives full consideration to the factors such as the cutting edge of the cutting edge of the tool,the minimum unformed chip thickness and the frictional force generated by the flank return force.Due to the different cutting depth the cutting principle is different,the micro cutting force model will be developed according to different region.Finally,the experiment is designed based on the micro servo turning with self-designed a dual-axis force transducer-embedded fast tool servo(DFT-FTS) device.
micro cutting force model;fast tool servo;size effect;free form surface
TG501.3
A
1672-9870(2017)04-0001-06
2017-05-08
谢晓麟(1988-),男,研究实习员,E-mail:xiexiaolin1988@

