基于多元统计过程监控的锅炉过程故障检测
牛玉广, 王世林, 林忠伟,, 李晓明
(1. 华北电力大学 新能源电力系统国家重点实验室, 北京 102206;2. 华北电力大学 控制与计算机工程学院, 北京 102206;3. 东北电力大学 自动化工程学院, 吉林省吉林 132012)
基于多元统计过程监控的锅炉过程故障检测
牛玉广1, 王世林2, 林忠伟1,2, 李晓明3
(1. 华北电力大学 新能源电力系统国家重点实验室, 北京 102206;2. 华北电力大学 控制与计算机工程学院, 北京 102206;3. 东北电力大学 自动化工程学院, 吉林省吉林 132012)
提出了一种新的基于稀疏约束非负矩阵分解(SCNMF)的复杂工业过程故障检测方法.首先在交替约束最小二乘算法(ACLS)求解非负矩阵分解(NMF)问题的基础上对系数矩阵H实施稀疏约束,随后采用非负双奇异值分解(NDSVD)方法对SCNMF算法进行初始化,并将所提算法应用于某火力发电厂1 000 MW机组锅炉过程中.结果表明:SCNMF算法的收敛性和稀疏度明显优于传统的NMF算法,且对故障的检测效率也要优于NMF算法和主元分析(PCA)算法.
故障检测; 非负矩阵分解; 奇异值分解; 锅炉过程
Abstract: A novel fault detection method based on sparseness-constrained non-negative matrix factorization (SCNMF) was proposed for complex industrial processes. The specific way is to use alternating constrained least squares (ACLS) with sparseness constraint on coefficient matrixHto solve the non-negative matrix fracterization (NMF) problems, then to enhance the initialization stage of SCNMF by non-negative double singular value decomposition (NDSVD), and finally to apply the presented method to the fault detection in various boiler processes of a 1 000 MW unit. Results show that the SCNMF is superior to conventional NMF on both the convergence and the sparsity, and its monitoring performance is also better than NMF and principal component analysis (PCA).
Key words: fault detection; non-negative matrix factorization; singular value decomposition; boiler process
近年来,基于多元统计过程监控(Multivariate Statistical Process Monitoring,MSPM)的故障检测方法得到了快速发展,其原因在于:一是现代化工业过程系统变得越来越庞大,系统复杂度呈几何式增长,想要根据物理化学规律建立其精确的机理模型或是选择合适的经验模型十分困难;二是这些系统每天都会产生大量反映生产过程和设备运行的数据,如何充分利用这些实时和历史数据,提取出能够反映系统运行状态的特征信息,以实现对生产过程和运行设备的故障检测,已成为迫切需要解决的问题[1].
基于MSPM的故障检测方法从理论上可以看成是将实时或历史数据从高维的测量空间变换到低维的特征空间,以得到故障特征进而对系统进行故障检测.传统的MSPM方法主要有主元分析(PCA)、偏最小二乘(PLS)、Fisher判据分析(FDA)、规范变量分析(CVA)和独立主元分析(ICA)等[2-8].以上方法因施加的限制条件不同而得到了反映过程变量之间不同相关性的子空间分解结构,但它们存在2个共同特征:(1) 分解所得矩阵元素可正可负;(2) 对过程变量进行了一定的假设.非负矩阵分解(NMF)[9]是一种新的矩阵分解技术,与传统的MSPM方法不同,除了要求原始数据和分解因子满足非负条件外,NMF没有对过程变量作其他任何假设.Ding等[10]证明了如果给NMF中的系数矩阵H增加正交约束,那么NMF和K-means在理论上就是等价的.NMF的非负约束导致分解结果是对原数据样本基于“部分”(即每一个特征)的表示形式,使得数据样本只允许对各个特征进行纯加性的线性组合,同时也导致分解因子在一定程度上具有天然的稀疏性.而且NMF在计算过程中采用基于矩阵元素的计算方式,使得其在面对数据存在缺失或局部噪声的情况下具有一定的鲁棒性.因此,NMF已经广泛应用于信号处理、生物医学工程、模式识别、计算机视觉和图像工程等领域[11].
然而,在工业过程故障检测领域基于NMF的故障检测方法还鲜有应用.Li等[12]将NMF算法用于化工过程的故障检测.为了扩展NMF算法的应用范围,Li等[13]放宽了NMF算法对数据的非负性约束,提出了广义非负矩阵投影算法,但文中虽然提到了初始化和稀疏性对NMF算法的重要性,却没有在这方面进行深入研究.笔者将稀疏约束非负矩阵分解(SCNMF)算法应用于工业过程故障检测中,同时针对SCNMF算法对初始迭代矩阵的选取比较敏感这一特点,提出了基于非负双奇异值分解(NDSVD)的NMF初始化算法,并用国内某1 000 MW火电机组锅炉过程实际运行数据验证了所提算法的可行性及其故障检测性能.
1 NMF算法
对一个由m个变量组成的列向量x(x≥0)进行n次采样,记每次采样所得样本向量为xi(i=1,2,…,n),取X=[x1,x2,…,xn]∈Rm×n,NMF算法通过求解
(1)
(其中FX(W,H)用来描述X与WH之间的差异)来得到2个非负矩阵W和H,使
Xm×n≈Wm×k·Hk×n
(2)
成立[9,14].其中W为基矩阵,H为系数矩阵,k为原始数据低维近似描述的维度,k的取值一般应满足(m+n)k 对式(1)中NMF问题的求解可以归结为一个优化问题.关于目标函数FX的选取,Lee等[14]采用欧氏距离的平方和广义Kullback-Leibler散度来描述X与WH间的差异,而后利用类似于期望最大化(EM)算法中使用的优化策略对目标函数FX进行交替求解,得到2个迄今最为经典和使用最为广泛的单调算法.其中采用欧氏距离(F-范数)作为目标函数的数学形式如下: s.t.W≥0,H≥0 (3) 由式(3)可知,当且仅当X=WH时,目标函数值取得最小值0.因此,在求解过程中目标函数的值越接近0,所求得的解就越精确.然而,研究结果表明上述FX单独以W或H为变量时是凸函数,但同时以W和H为变量时却不是凸函数.因此求解上述优化问题不能得到全局最优解,只能得到局部最优解.对此Lee等给出了相应的迭代规则(见式(4)和式(5)),并在理论上证明了目标函数在该迭代规则下是单调不增的,详细证明请参考文献[14]. 欧氏距离迭代规则如下: (4) (5) 上述迭代规则被称为乘法迭代算法,能较好地协调算法收敛速度与易用性之间的矛盾. 交替最小二乘法(ALS)最早由Paatero等[15]用于非负矩阵分解.式(3)中的优化问题可以分解为2个交替最小二乘子问题: 固定) (6) (7) 为了克服交替最小二乘法数值稳定性差的缺点,Albright等[16]提出了交替约束最小二乘算法(ACLS)来求解NMF问题.式(3)中NMF问题可改写为: s.t.W≥0,H≥0 (8) 式(8)中NMF问题可以分解为2个交替正则化最小二乘子问题: (9) (10) ACLS算法的迭代规则如下: (WTW+βIk)H=WTX (11) (HHT+αIk)WT=HXT (12) 式中:Ik为一个k×k的单位阵; Albgright等[16]通过实验证明,与其他NMF算法相比,ACLS算法的计算效率最高,在稀疏性方面也有一定程度的提高,其避免了其他算法在计算过程中所出现的元素闭锁现象.在收敛性方面,虽然没有证明ACLS算法最终得到的稳定点是局部最小值还是鞍点,但实验结果表明ACLS算法所得结果是优于其他NMF算法的. 非负矩阵分解最重要的性质是其往往会产生数据的稀疏表示.因此,在希望利用非负矩阵分解得到数据的稀疏表示时,有必要考虑具有稀疏性约束的非负矩阵分解算法.由前文分析可知,ACLS算法虽然在一定程度上提高了NMF算法的稀疏性,但其所得结果的稀疏程度并不令人满意.因此,为了得到数据更加稀疏的描述,在ACLS算法的基础上提出了SCNMF算法.适当地增加稀疏性约束可以提高NMF算法的性能,但如果同时对基矩阵W和系数矩阵H施加较高的稀疏性约束将会导致NMF算法对数据的描述能力急剧下降[10].因此,在所提出的SCNMF算法中只对H施加稀疏性约束,其数学形式如下: s.t.W≥0,H≥0 (13) 式中:H(: ,j)为系数矩阵H的第j列;β用来平衡算法精度与H稀疏程度之间的取舍. 式(13)可以分解为2个交替最小二乘子问题: (14) 式中:e为一个元素值全为1的行向量;01×n为一个零向量. 式(14)的最小化相当于使H每一列的L1范数最小化,即对H规定稀疏度. (15) 式中:0k×m为一个k×m的零矩阵. 由矩阵微分可得: (16) 式中:Ek为一个元素值全部为1的k×k矩阵. (17) 得出稀疏交替最小二乘子问题的目标函数的梯度矩阵为: (18) (19) (WTW+βEk)H=WTX (20) (HHT+αIk)WT=HXT (21) 采用SCNMF算法优化问题的求解步骤如下:(1) 初始化基矩阵W∈Rm×k;(2) 根据式(20)求解H;(3) 强制系数矩阵H非负化Hkj=max{0,Hkj};(4) 根据式(21)求解W;(5) 强制系数矩阵W非负化Wik=max{0,Wik};(6) 将W的各列归一化为单位F-范数,然后返回步骤(2)并重复迭代,直至满足收敛准则;(7) 输出基矩阵W和系数矩阵H. 所有的NMF算法都是通过迭代求解的,众所周知NMF算法对W和H初始化矩阵的取值比较敏感,一个好的初始值可以提升算法的速度和准确性.但在实际应用中许多研究者仍然采用最基本的随机法对NMF算法进行初始化.由于NMF算法只能收敛于局部最优解,不同的初始值将导致不同的结果.Albright等[16]通过比较几种常用的初始化方法,发现基于奇异值分解(SVD)的初始化方法得到的解要优于其他方法得到的解.笔者在SVD算法基础上提出了一种新的NDSVD初始化方法,该方法包含2个SVD过程:一个用来生成W的初始近似矩阵,另一个利用单位秩矩阵的代数性质使近似矩阵逼近初始矩阵W0.NDSVD的步骤如下. (1) 输入测量矩阵X∈Rm×n,常数k (2) 采用SVD算法分解X并取前k个最大的奇异值所对应的矩阵为[Um×k,Sk×k,Vn×k]. (4) 从j=2开始重复执行以下步骤直至j=k: 1) 令U(:,j)=x+-x-,V(:,j)=y+-y-(其中x+和y+分别代表U和V第j列中所有正元素的绝对值,x-和y-分别代表U和V第j列中所有负元素的绝对值); 采用SCNMF算法对数据样本矩阵X进行矩阵分解,将原始数据从高维的测量空间变换到低维的特征空间.因此,基于SCNMF算法可以构建一个统计过程监控模型: (22) 由于SCNMF算法将测量空间分解所得的特征空间和残差空间与PCA算法分解所得主元子空间和残差子空间类似,特征空间主要反映过程状态的变化情况,残差空间则主要反映过程噪声的变化情况.因此,笔者仿照PCA算法中监控统计量T2和Q的定义,构造基于SCNMF算法统计监控模型的监控统计量来监控特征空间和残差空间的变化,新的监控统计量定义如下: (23) (24) (25) 基于SCNMF算法的故障检测方法主要包括离线建模和在线诊断2部分,其详细流程如下. 以某火力发电厂1 000 MW机组锅炉过程实际运行数据为对象来检验SCNMF算法的性能.首先,利用NMF算法和SCNMF算法分别对系统稳定运行数据进行分解,从稀疏度和收敛性的角度分析了SCNMF算法的优越性;随后,通过模拟传感器的两类故障来检验SCNMF算法的故障检测性能,并与传统的NMF算法和PCA算法进行对比. 以火力发电厂锅炉过程为实例,说明SCNMF算法在故障检测当中的应用情况.所采集的过程变量涉及某电厂锅炉过程中给水系统、主汽压系统和主汽温系统3个系统,共计33个主要过程变量,其中包括温度信号14个、压力信号9个、流量信号9个以及功率信号1个(见表1). 选取机组负荷为800 MW时机组稳定运行50 min的运行数据为建模数据,采样时间为3 s,共1 000个采样点. 稀疏指的是利用一个向量中少数非零元素来有效表示该向量[17].也就是说在此向量中大多数元素的值接近或等于零,只有少数元素的值为非零值.利用L1范数和L2范数之间的关系来度量一个向量的稀疏程度,表达式如下: (26) 式中:Hi为矩阵H的第i列. 由式(26)可以看出,当Hi中只有一个元素为非零其余元素均为零时,向量稀疏度取得最大值为1,当Hi中所有元素均为非零时,向量稀疏度取得最小值为0.系数矩阵H的稀疏度定义如下: (27) 众所周知,PCA算法中主元个数的选取是十分重要的,同样在NMF算法及其改进算法中确定原始数据样本矩阵中的低维近似维度k也至关重要.但是与PCA算法拥有成熟的主元选取方法不同,基于NMF的算法还没有一种被广泛认可的确定k的取值方法,实际应用中一般是靠研究者的经验来确定的.由于下文将对比PCA算法与所提SCNMF算法,因此k的取值将参照PCA算法中主元个数的取值来确定. 对所采集的锅炉过程实际运行数据分别采用SCNMF算法和传统的NMF算法进行建模.其中SCNMF算法采用NDSVD进行初始化,NMF算法则采用传统的随机方法,确定维度k,算法的迭代次数均设为300.关于正则化参数α和β的选取,由式(20)和式(21)可以看出,α和β的取值越小,对W的压制作用及对H的稀疏性约束就越小,当α和β=0时,SCNMF算法将等效于传统的NMF算法,由于α和β取值没有上限,当α和β过大时将导致SCNMF算法对数据的描述能力急剧下降,因此通过反复尝试最终确定α=5.0、β=1.5.对实际运行数据的建模结果见图1和图2. 由图1可知,SCNMF算法在收敛性和计算精度上要明显优于NMF算法.SCNMF算法的初始误差为57.95,NMF算法的初始误差为177.42,是SCNMF算法的3倍多;当算法迭代终止时,NMF算法的最终迭代误差为47.97,而SCNMF算法的最终迭代误差为33.36,比NMF算法降低了1/3左右.在收敛速率上,SCNMF算法在迭代初期误差衰减速率要远远高于NMF算法,迭代10次之后迭代误差便趋于稳定不再发生变化,而NMF算法的收敛较慢,在进行250次迭代之后迭代误差才趋于稳定. 图2给出了由SCNMF算法和NMF算法分解所得到的系数矩阵H每一列的稀疏度.由图2可以看出,SCNMF算法中H每一列的稀疏度均高于NMF算法中H每一列的稀疏度.SCNMF算法和NMF算法计算所得的H的稀疏度分别为0.549 9和0.320 4.将式(2)改写成向量形式为xi=Whi(xi和hi分别为X和H的列向量),因此可以将每个数据样本看成是所有基向量(W的列向量)的加权和,权重系数就是H相对应的列向量hi.若将W的每一列看成一个局部特征,则提高H每一列的稀疏度就意味着可以用更少的局部特征来表征数据样本,从而提高数据的压缩性和可解释性. 图1 SCNMF算法和NMF算法收敛性和计算精度的对比 Fig.1 Comparison of convergence and accuracy between SCNMF and NMF 图2 SCNMF算法和NMF算法中H稀疏度的对比 综上所述,与传统的NMF算法相比,所提出的基于ACLS的SCNMF算法和NDSVD初始化方法能够更快速地获得更准确和稀疏程度更高的矩阵分解结果.因此,SCNMF算法比较适合应用在多元统计过程监控中. 采用SCNMF算法、传统NMF算法以及PCA算法对传感器的2类故障进行检测,并对检测结果进行对比,进而说明SCNMF算法的有效性.将第4.1节中所采集的锅炉过程实际运行数据分为训练集和测试集,每部分包含500个采样点. 故障1:选取主蒸汽温度A作为实验对象,从测试集第51个采样样本开始对该信号叠加实测值的1%来模拟传感器恒偏差故障,3种算法的检测结果见图3. (a) PCA算法 (b) NMF算法 (c) SCNMF算法 图3 故障1的检测结果 Fig.3 Detection results for fault 1 故障2:选取主蒸汽流量作为实验对象,从测试集第21个采样样本开始对该信号叠加一个斜坡信号(信号上限为主蒸汽流量所有采样样本平均值的2%)来模拟传感器的漂移故障,3种算法的检测结果如图4所示. (a) PCA算法 (b) NMF算法 (c) SCNMF算法 图4 故障2的检测结果 Fig.4 Detection results for fault 2 综上所述,SCNMF算法和NMF算法的故障检测效果要明显优于传统的PCA算法.由于SCNMF算法中对系数矩阵H施加了稀疏性约束,提高了H中列向量的稀疏度,使得SCNMF算法可以用更少的基向量组合来表征数据样本,增强了数据的压缩性和可解释性. 在ACLS基础上提出了SCNMF算法,并用国内某火力发电厂锅炉过程实际运行数据对基于SCNMF的故障检测方法进行测试.实验结果表明,基于SCNMF算法的故障检测模型的监控结果要优于NMF算法和PCA算法.为NMF算法及其改进算法应用于工程实际积累了一定的经验.但是,火力发电厂生产过程是一类典型的变工况工业过程,此处只在单一稳定工况下对SCNMF算法进行了故障测试,并没有考虑多工况下SCNMF算法的故障检测性能以及故障识别等问题,这些问题将在下一步的工作中作进一步研究. [1] 周东华, 李钢, 李元. 数据驱动的工业过程故障诊断技术: 基于主元分析与偏最小二乘的方法[M]. 北京: 科学出版社, 2011. [2] JIANG Q C, YAN X F, ZHAO W X. Fault detection and diagnosis in chemical processes using sensitive principal component analysis[J].Industrial&EngineeringChemistryResearch, 2013, 52(4): 1635-1644. [3] HARROU F, NOUNOU M N, NOUNOU H N, et al. PLS-based EWMA fault detection strategy for process monitoring[J].JournalofLossPreventionintheProcessIndustries, 2015, 36: 108-119. [4] SHI H T, LIU J C, WU Y H, et al. Fault diagnosis of nonlinear and large-scale processes using novel modified kernel Fisher discriminant analysis approach[J].InternationalJournalofSystemsScience, 2016, 47(5): 1095-1109. [5] JIANG B B, HUANG D X, ZHU X X, et al. Canonical variate analysis-based contributions for fault identification[J].JournalofProcessControl, 2015, 26: 17-25. [6] 周云龙, 王锁斌. 高斯矩Fast ICA算法在风机振动信号去噪中的应用[J].动力工程学报, 2011, 31(3): 187-191. ZHOU Yunlong, WANG Suobin. Noise reduction for fan vibration signals based on Gaussian moment fast ICA algorithm[J].JournalofChineseSocietyofPowerEngineering, 2011, 31(3): 187-191. [7] ZHAO C, GAO F. Fault-relevant principal component analysis (FPCA) method for multivariate statistical modeling and process monitoring[J].ChemometricsandIntelligentLaboratorySystems, 2014, 133: 1-16. [8] 毕小龙, 葛晓霞, 朱正林, 等. 复合主元分析方法在电站冗余传感器故障检测中的应用[J].动力工程学报, 2010, 30(8): 601-606. BI Xiaolong, GE Xiaoxia, ZHU Zhenglin, et al. Application of hybrid principal component analysis to fault detection of redundant sensors in power plants[J].JournalofChineseSocietyofPowerEngineering, 2010, 30(8): 601-606. [9] LEE D D, SEUNG H S. Learning the parts of objects by non-negative matrix factorization[J].Nature, 1999, 401(6755): 788-791. [10] DING C, LI T, PENG W, et al. Orthogonal nonnegative matrix t-factorizations for clustering[C]//Proceedingsofthe12thACMSIGKDDInternationalConferenceonKnowledgeDiscoveryandDataMining. New York, USA: ACM, 2006: 126-135. [11] 李乐, 章毓晋. 非负矩阵分解算法综述[J].电子学报, 2008, 36(4): 737-743. LI Le, ZHANG Yujin. A survey on algorithms of non-negative matrix factorization[J].ActaElectronicaSinica, 2008, 36(4): 737-743. [12] LI X B, YANG Y P, ZHANG W D. Fault detection method for non-Gaussian processes based on non-negative matrix factorization[J].Asia-PacificJournalofChemicalEngineering, 2013, 8(3): 362-370. [13] LI X B, YANG Y P, ZHANG W D. Statistical process monitoring via generalized non-negative matrix projection[J].ChemometricsandIntelligentLaboratorySystems, 2013, 121: 15-25. [14] LEE D D, SEUNG H S. Algorithms for non-negative matrix factorization[C]//Proceedingsofthe13thInternationalConferenceonNeuralInformationProcessingSystems. Cambridge, UK: MIT Press, 2000: 556-562. [15] PAATERO P, TAPPER U. Positive matrix factorization: a non-negative factor model with optimal utilization of error estimates of data values[J].Environmetrics, 1994, 5(2): 111-126. [16] ALBRIGHT R, COX J, DULING D, et al. Algorithms, initializations, and convergence for the nonnegative matrix factorization[R].[S.l.]:North Caroline State University, 2006. [17] SAITO N. The generalized spike process, sparsity, and statistical independence[J].ModernSignalProcessing, 2004, 46: 317-340. Fault Detection of Industrial Processes Based on Multivariate Statistical Process Monitoring NIUYuguang1,WANGShilin2,LINZhongwei1,2,LIXiaoming3 (1. State Key Laboratory for Alternate Electric Power System with Renewable Energy Sources,North China Electric Power University, Beijing 102206, China; 2. School of Control and Computer Engineering, North China Electric Power University, Beijing 102206, China; 3. School of Automation Engineering, Northeast Dianli University, Jilin 132012, Jilin Province, China) 2016-10-18 2016-12-06 国家自然科学基金青年基金资助项目(51606033);中央高校基本科研业务专项资金资助项目(JB2015181) 牛玉广(1964-),男,河南滑县人,教授,博士,研究方向为新能源电力系统建模与控制,大型火电机组优化控制与故障诊断. 王世林(通信作者),男,博士研究生,电话(Tel.):010-61772962;E-mail:wslncepu@163.com. 1674-7607(2017)10-0829-08 TP277 A 470.20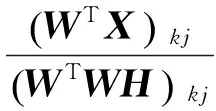

2 稀疏约束非负矩阵分解
2.1 交替最小二乘法求解NMF


2.2 SCNMF算法


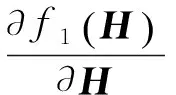


3 基于SCNMF算法的故障检测
3.1 SCNMF初始化算法
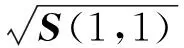
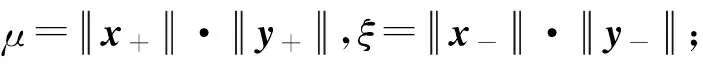

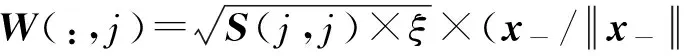
3.2 监控统计量设计
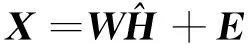
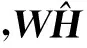

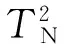
3.3 SCNMF算法故障检测流程
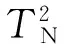

4 实验验证
4.1 锅炉过程
4.2 稀疏度和收敛性比较
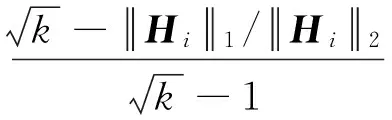



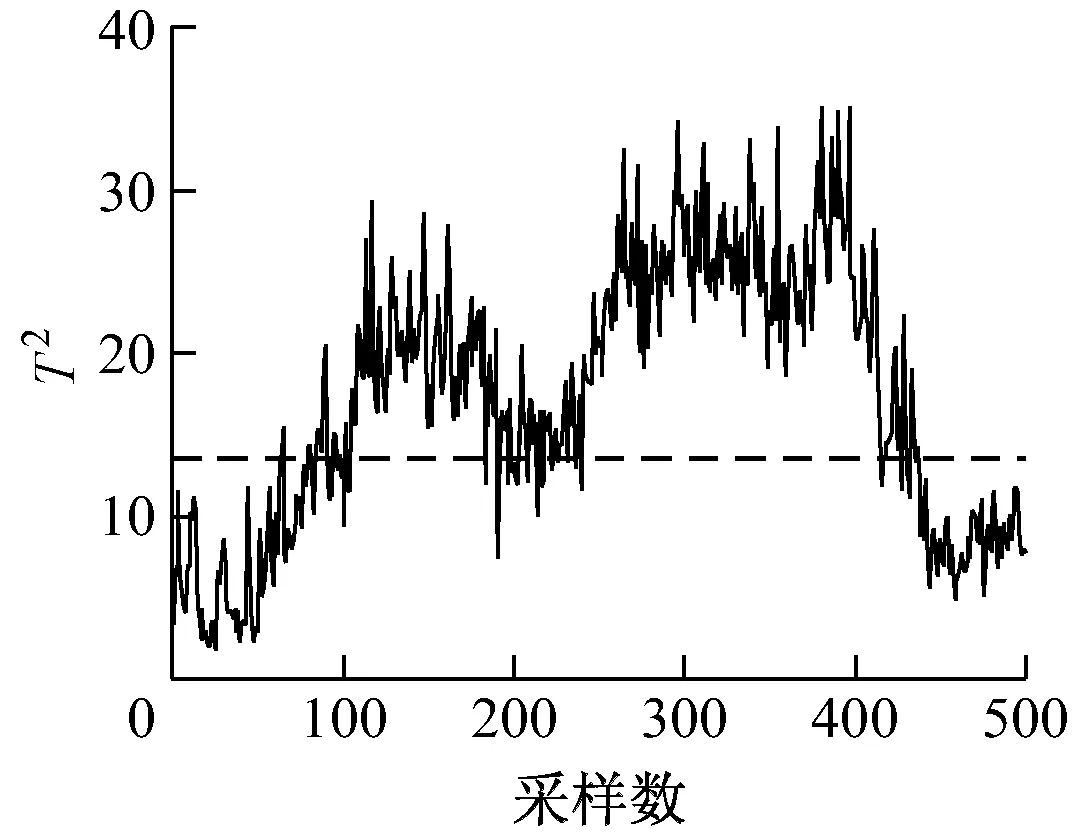
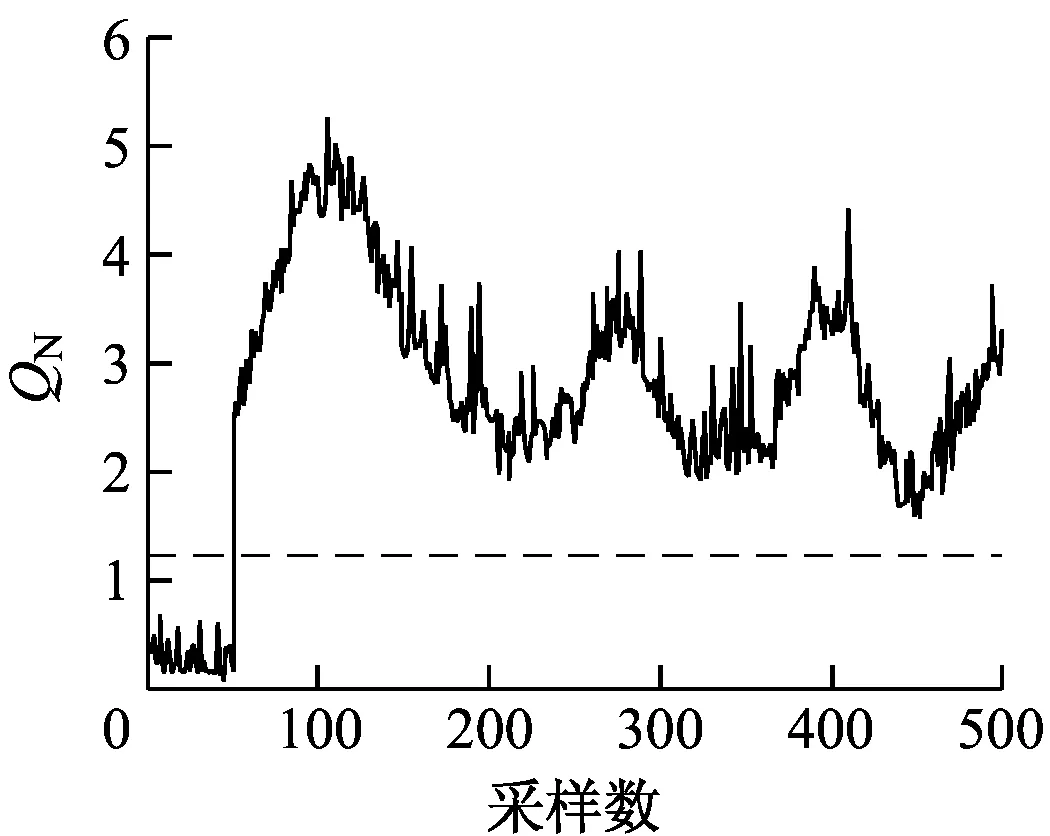
4.3 故障检测实例









5 结 论

