基于人工蜂群算法的高速变螺距分件供送螺杆优化设计
李全来
(北京工商大学材料与机械工程学院,北京 100048)
基于人工蜂群算法的高速变螺距分件供送螺杆优化设计
李全来
(北京工商大学材料与机械工程学院,北京 100048)
高速变螺距分件供送螺杆是包装机械中供送系统的重要基础构件,是整个设备的咽喉。研究提出用人工蜂群算法优化螺杆结构参数,高速变螺距分件供送螺杆优化模型以螺杆螺旋线总长最小为优化目标,以螺旋线最大圈数为设计变量,以供送过程中螺杆对包装容器保持有阻挡作用,以及加速度的最大变化率小于预定值为约束条件。结果表明,经过人工蜂群算法优化后获得的最优螺旋线最大圈数能有效减小高速变螺距分件供送螺杆的长度,为高速变螺距分件供送螺杆参数的合理选取提供了依据。
变螺距;分件供送螺杆;人工蜂群算法;优化
Abstract: High speed variable pitch timing screw is an important foundation component of feeding system in packaging machinery. It is the throat of the whole equipment. In this paper, the artificial bee colony algorithm is employed to optimize the structure parameters of the screw, providing a basis for the design of maximum number of circles. The high speed variable pitch timing screw optimization model takes the minimum total length of the variable pitch screw helix as the optimization goal, with maximum number of helix circles as design variables, the plugging effect on the packaging container is kept, as well as the rate of acceleration change is no more than the predetermined value as the constraint conditions. The results show that the maximum numbers of helix circles obtained by artificial bee colony algorithm can effectively reduce the total length of variable pitch timing screw. It is useful for the reasonable selection of high speed variable pitch timing screw structure parameters.
Keywords: variable pitch; timing screw; artificial bee colony algorithm; optimization
高速变螺距分件供送螺杆(简称为高速供送螺杆)是高速灌装机、充填机、贴标机、封口机等包装机械中供送系统的重要零件,其转速一般为250~550 r/min或更高[1]79。其主要功能是根据预定的工艺要求,将呈规则或不规则排列的成批刚性包装容器,沿着既定的路线,按照规定的间距,以所需的状态和速度供送到主机包装工位[2-3]。在此过程中,高速供送螺杆可以使包装容器增距、减距、变速等[1]79-84。随着工业化水平的不断提高,人们对包装机械的生产效率和自动化程度提出了更高的要求[4-5]。合理设计高速供送螺杆结构参数可以有效减少供送过程中的冲击、振动和卡滞现象,可以获得紧凑的螺杆结构,提高供送的稳定性和可靠性,从而提高包装机械的生产效率和自动化水平[6]。
目前中国高速供送螺杆主要依赖进口,有关高速供送螺杆优化设计理论的研究较少,制约了螺杆供送性能的提高。高永绪[7]按匀速-变加速-匀加速运动规律设计了三段式高速供送螺杆。赵静等[8]研究表明在三段式高速供送螺杆的匀加速段包装容器间有干涉,为此修正了匀加速段螺旋线方程。李军霞等[9]在三段式高速供送螺杆的基础上增加了减加速度段,设计了四段式高速供送螺杆,消除螺杆末端加速度的突变,减小供送过程中的刚性冲击。章建浩[10]为减小包装容器进入高速供送螺杆时对螺杆产生的冲击力,提高供送的稳定性,在等速段之前添加了减速段。各段螺旋线的最大圈数是高速供送螺杆的重要结构参数之一。通常采用类比法参考已有的高速供送螺杆选取各段螺旋线的最大圈数,这使螺杆的螺旋线总长较大。章建浩[10]用复合型法优化各段螺旋线的最大圈数,使供送螺杆的螺旋线总长较小。但是传统优化方法收敛速度慢,易陷入局部最优,不能有效获得最优的螺旋线最大圈数,限制了螺杆高速供送性能的提高。
人工蜂群算法是近十年来迅速发展起来的一种模仿蜜蜂采蜜行为的元启发式群智能优化算法。与遗传算法[11-12]、人工神经网络[13]、粒子群算法[14]等优化方法相比,具有结构简单、控制参数少、鲁棒性强等优点,而且在每次迭代中都进行全局和局部搜索,能有效避免算法陷入局部最优[15]57-58。为了在满足生产能力和供送稳定可靠的条件下有效选取螺旋线最大圈数,获得紧凑的螺杆结构,本研究提出用人工蜂群算法对螺旋线最大圈数进行约束优化,为高速供送螺杆的优化设计提供依据。
1 高速供送螺杆的螺旋线参数
针对圆柱形刚性包装容器的高速供送螺杆进行优化。由匀速—变加速—等加速—变加速构成的4段组合式螺杆适合高速供送,可以实现供送过程中螺杆与输送链带的平稳衔接[12]。第1段为匀速段,采用等螺距螺旋线,使进入螺杆工作区的包装容器匀速、平稳运动,减少包装容器的“陡振”现象。第2段为变加速段,该段为匀速段和等加速段之间的过渡段,使包装容器的加速度由零逐渐增加到等加速段要求的加速度,避免因加速度突变导致的冲击现象[1]79-84。第3段为等加速度,星形拨轮位于螺杆的末端,其节距通常大于高速供送螺杆入口段相邻两个包装容器的中心距,用等加速度规律设计该段变螺距螺旋线,逐渐增大相邻包装容器的间距。第4段为余弦变加速段,使高速供送螺杆末端包装容器加速度值为零,以减小包装容器对星形拨轮的冲击[9]。
匀速段供送加速度a1、供送速度v1、轴向位移H1分别为:
(1)
式中:
s01——匀速段螺距,与包装容器主体部位的圆弧半径和两相邻包装容器主体部分的外廓间距有关,mm;
z1——等速段螺旋线圈数;
n——高速供送螺杆的转速,r/min。
正弦变加速段供送加速度a2、供送速度v2、轴向位移H2分别为:
(2)
式中:
a——高速供送螺杆的最大供送加速度,mm/s2;
z2,Z2——分别为正弦变加速段螺旋线圈数和最大圈数。
等加速段供送加速度a3、供送速度v3、轴向位移H3分别为:
(3)
式中:
z3——等加速段螺旋线的圈数。
余弦变加速段供送加速度a4、供送速度v4、轴向位移H4分别为:
(4)
式中:
Z3——余弦变加速段的螺旋线最大圈数;
z4,Z4——分别为余弦变加速段螺旋线圈数和最大圈数。
在高速供送螺杆的末端,供送速度为:

(5)
同时在高速供送螺杆的末端,包装容器应与星形拨轮速度同步,即供送速度与星形拨轮的节圆线速度相等[1]81,即
v4|z4=Z4=u轮。
(6)
星形拨轮的节圆线速度u轮可表达为[1]81:

(7)
式中:
Cb——星形拨轮节距,mm。
故联立式(5)~(7)可得高速供送螺杆的最大供送加速度a为[1]83:

(8)
将各段螺旋线最大圈数分别代入式(1)~(4)可得高速供送螺杆的4段螺旋线总长H为:
H=H1|z1=Z1+H2|z2=Z2+H3|z3=Z3+H4|z4=Z4

(9)
式中:
Z1——等速段的螺旋线最大圈数。
在供送过程中,包装容器受到输送链带的摩擦推力作用而前进。高速供送螺杆起隔挡作用,对包装容器的前进产生阻力[10]。忽略包装容器和高速供送螺杆螺旋面间摩擦力的影响,在水平方向上包装容器只受输送链带的摩擦推力F带和高速供送螺杆的阻力F杆作用,包装容器的加速度为[10]:
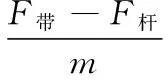
(10)
式中:
fd——包装容器与输送链带之间的摩擦系数。
将式(8)代入式(10)并整理得:

(11)
在正弦和余弦变加速度段,加速度的变化率J1和J2分别为:

(12)

(13)
加速度的最大变化率分别为J1max和J2max分别为:
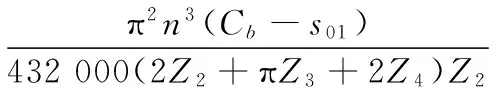
(14)

(15)
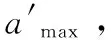
(16)
(17)
2 高速供送螺杆螺旋线最大圈数的优化
2.1 优化模型的建立
由式(9)可知,优选各段螺旋线的最大圈数可以获得较为紧凑的螺杆结构。在高速供送螺杆设计过程中,多用类比法选取各段螺旋线的最大圈数,这使得设计出的螺旋线总长较大,高速供送螺杆的惯量也较大,刚性较小。通过建立高速供送螺杆螺旋线最大圈数的数学优化模型,用人工蜂群算法寻找最优的螺旋线的最大圈数。
该优化模型以高速供送螺杆螺旋线总长H最小为优化目标,优化目标函数为式(9)。本优化问题的设计变量为螺旋线的最大圈数。Z1是保证包装容器顺利导入高速供送螺杆的经验值,与包装容器形状和质量有关,而对式(11)、(16)和(17)均无影响,因而不作为优化模型的设计变量。Z2、Z3、Z4对式(11)、(16)和(17)均有影响,选为优化模型的设计变量,可用向量表达为Z=[Z2,Z3,Z4]T。在供送过程中设计变量应满足式(11)、(16)和(17),同时Z2、Z3、Z4表示正弦加速段、等加速段、余弦加速段螺旋线的最大圈数,均应为正数,这构成了优化模型的6个约束条件。综上,高速供送螺杆螺旋线最大圈数优化问题的数学优化模型可以表示为:
maxH(Z)
(18)
2.2 基于人工蜂群算法的螺旋线最大圈数优化
人工蜂群(Artificial Bee Colony Algorithm,ABC)算法是由土耳其学者Karaboga在2005年提出的一种新型元启发式群体智能模型。它通过模拟自然界中蜜蜂群体寻找优良蜜源的过程求解优化问题[15]16-19[17]。ABC算法具有结构简单、控制参数较少、收敛速度快、鲁棒性强等优点。
ABC算法中蜜源代表优化问题的候选解。蜜源的质量即为解的质量,用适应度函数值衡量。适应度函数值越大说明蜜源质量越高。在ABC算法中,蜜蜂分为采蜜蜂(Employed bees)、观察蜂(Outlookers)和侦查蜂(Scouts)三类。采蜜蜂与其采集的蜜源一一对应,记录了当前正在采集的蜜源信息,并将此信息与观察蜂分享。同时采蜜蜂在当前蜜源附近搜索更优蜜源,并替换当前蜜源。观察蜂根据采蜜蜂分享的蜜源信息,按照某种策略选择一个蜜源,在该蜜源邻域进行采集,搜索更优蜜源,记录更优蜜源的信息,替换原蜜源信息。若某蜜源连续多次未被替换,则相应的采蜜蜂或观察蜂放弃该蜜源,并转化为侦察蜂。侦察蜂在搜索空间内随机寻找新蜜源,供其他蜜蜂采集[15]47-62[17]。
ABC算法优化螺旋线最大圈数的优化步骤:
(1) 初始化种群参数:生成N个蜜源,每个蜜源都是一个三维向量,代表设计变量Z的一个候选解。第i个蜜源Xi可表示为Xi=[x1i,x2i,x3i]T, 其中x1i,x2i,x3i分别为Z2,Z3,Z4的候选值。
Xi的第j维分量xji可由式(19)获得[15]47-62[17]:
(19)
式中:
R1——[0,1]之间的随机数;
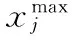
蜜蜂与蜜源一一对应,故将蜜蜂总数也设置为N,观察蜂和侦查蜂数量均为N/2,即Nemp=Nout=N/2[15]53[17]。蜂群最大迭代次数MaxCycle,蜜源停留最大限制搜索次数limit。蜜源未被连续更新次数trial值置0。
将设计变量Z的候选解Xi代入式(18) 中的约束条件,判断是否符合约束,若不符合则按式(19)重新生成蜜源,直至符合约束条件。
(2) 计算蜜源质量:将Xi代入式(18)中的目标函数,计算目标函数值,并通过式(20)计算该蜜源的适应度函数值fit(Xi)[15]47-62[17]。

(20)
根据适应度函数值的大小对蜜源排序,适应度函数值大的前Nemp个蜜源是采蜜蜂的采集蜜源。
(3) 采蜜蜂邻域搜索:采蜜蜂在蜜源Xi邻域搜索更优蜜源时,随机选择该蜜源的某一维j,并在适应度函数值大的前Nemp个蜜源中随机选择另一蜜源Xk(k∈[1,Nemp]),根据式(21)计算出更新后的蜜源newXi的第j维分量newxji[15]47-62[17]。
newxji=xji+2(R2-0.5)(xji-xjk),
(21)
式中:
R2——[0,1]之间的随机数。
若newxji≤0,则不符合设计变量均为正数的约束条件,按式(21)重新生成。新蜜源的其他维分量保持不变。按式(20)计算适应度函数值。将newXi代入式(18),计算g1、g2和g3,按式(22)计算新蜜源newXi的约束违反检查函数值[18]。
CV(newXi)=max[0,g1(newXi)]+max[0,g2(newXi)]+max[0,g3(newXi)]。
(22)
若新蜜源符合约束条件,则该蜜源为可行解,约束违反检查函数值为0,否则为非可行解,约束违反检查函数值为一个正值。
选用直接比较法判断newXi和Xi的优劣。如果2个蜜源均为可行解,适应度函数值高的蜜源优于适应度函数值低的;如果一个蜜源为可行解,另一个为非可行解,可行解优于非可行解;如果它们都为非可行解,约束违反检查函数值小的蜜源优于约束违反检查函数值大的。如果原蜜源没有被新蜜源代替,trial值增加1。反之,trial值置0。
(4) 观察蜂邻域搜索:根据式(23)计算观察蜂Xt(t∈(Nemp,N])选中采蜜蜂的采集蜜源Xi的概率[15]52[17]。

(23)
生成0~1的随机数R3。如果R3 newxjt=xji+2(R4-0.5)(xji-xjk), (24) 式中: R4——[0,1]之间的随机数。 与步骤(3)类似,若newxjt≤0,则不符合设计变量均为正数的约束条件,按式(24)重新生成。新蜜源newXt的维分量保持不变。按式(20)计算适应度函数值;按式(22)计算新蜜源newXi的约束违反检查函数值,根据步骤(3)中的判断标准确定是否更新蜜源,以及trail值是否增加。 (5) 判断所有蜜源的trial值,放弃trial值大于limit的蜜源。与之相对应的采蜜蜂或观察蜂转化为侦查蜂,根据式(19)在搜索空间内随机产生新蜜源。如果蜜源不符合约束条件,则重新随机生成,直至符合约束条件为止。计算该蜜源的适应度函数值。 (6) 记录当前最优蜜源,iter+1。 (7) 转回第(3)步,直至iter>MaxCycle,输出最优蜜源Xopt即为优化问题的最优解Zopt。 图1为ABC算法优化螺旋线最大圈数的流程图。 图1 人工蜂群算法流程图 选用蜜源数量N为50,即生成了50个设计变量的候选解。蜜蜂总数也为50,采蜜蜂数量为25,最大迭代次数Maxcycle为100,蜜源停留最大限制搜索次数limit为5。包装容器与输送链板之间的摩擦系数fd为0.215 mm,螺杆的转速n为250 r/min,星形拨轮的节距Cb为125 mm,匀速段螺杆螺距s01为60 mm。匀速段最大圈数为1。 经过Matlab编程计算,得出算法收敛情况见图2。 优化后各段螺旋线最大圈数为Z2opt=1.51,Z3opt=2.88,Z4opt=1.25,高速供送螺杆四段螺旋线的总长Hopt=420.35 mm。与采用类比法设计时选用的Z2=2,Z3=3,Z4=2,H=590.52 mm相比,高速供送螺杆的螺旋线总长度减小了28.8%。优化后高速供送螺杆的供送加速度、速度和位移曲线见图3。由图3可知,在供送过程中,包装容器的速度逐渐增大,位移逐渐增加,加速度无突变,不存在刚性冲击。因此人工蜂群算法能有效优化高速供送螺杆螺旋线的总长,为高速供送螺杆各段螺旋线最大圈数的选取提供依据。 (1) 建立了高速变螺距分件供送螺杆螺旋线最大圈数的优化模型。优化目标函数为螺旋线总长最小,设计变量为螺旋线的最大圈数,约束条件包括螺旋线最大圈数为正数,供送过程中螺杆对包装容器保持有阻挡作用,以及包装容器加速度的最大变化率不大于预定值。 图2 人工蜂群算法迭代收敛过程 图3 优化后高速供送螺杆的加速度、速度和位移曲线 (2) 本研究提出用人工蜂群算法求解高速变螺距分件供送螺杆优化模型。用适应度函数和约束违反检查函数评价解的优劣。通过采蜜蜂、观察蜂和侦察蜂的分工合作搜索最优螺旋线最大圈数。 (3) 用人工蜂群算法优化后,高速变螺距分件供送螺杆螺旋线总长减小28.8%,而且在供送过程中包装容器无加速度突变,能实现平稳供送,为高速变螺距分件供送螺杆参数的合理选取提供了依据。 [1] 黄颖为. 包装机械结构与设计[M]. 北京: 化学工业出版社, 2007. [2] 赵静, 张金, 支雷, 等. 基于UG的变距供送螺杆数控编程研究[J]. 红河学院学报, 2015, 13(5): 40-42. [3] 周为, 赵静, 张金. 变距供送螺杆参数化设计[J]. 赤峰学院学报: 自然科学版, 2014, 30(10): 24-26. [4] 余剑武, 舒新, 罗红, 等. 灌装机中弧面凸轮建模与造型研究[J]. 食品与机械, 2016, 32(6): 77-82. [5] 吴锦虹, 林楚平. 全自动自立袋充填旋盖机送袋机构及灌装阀的改进[J]. 食品与机械, 2015, 31(6): 117-119, 168. [6] 万久远. 特种供送螺杆关键技术研究[D]. 秦皇岛: 燕山大学, 2015: 1-7. [7] 高永绪. 变螺距供送螺杆的原理与计算[J]. 包装与食品机械, 1993, 11(2): 18-20. [8] 赵静, 张金, 査新龙, 等. 变距供送螺杆数学模型的研究[J]. 盐城工学院学报: 自然科学版, 2014, 27(4): 37-41. [9] 李军霞, 姚云峰, 史荣. 分件供送变螺距螺杆螺旋线形式的探讨[J]. 包装工程, 2009, 30(11): 50-52. [10] 章建浩. 高速分件供送螺杆装置的优化设计[J]. 包装与食品机械, 1990(Z1): 29-33. [11] 郭广颂, 陈良骥. 一种综合咖啡智能拼配方法研究[J]. 食品与机械, 2017, 33(3): 195-198. [12] 王娟, 李同杰, 姚智华, 等. 行星齿轮减速器均载性能动态的优化设计[J]. 食品与机械, 2016, 32(2): 71-74. [13] 王小勇, 李兵, 曾晨. 茶叶理条工艺的人工神经网络优化[J]. 食品与机械, 2016, 32(1): 103-105, 153. [14] 刘静, 管骁, 易翠平. 近红外光谱技术结合支持向量机对食用醋品牌溯源的研究[J]. 食品与机械, 2016, 32(1): 38-40, 52. [15] 江铭炎, 袁东风. 人工蜂群算法及其应用[M]. 北京: 科学出版社, 2014. [16] 钟昌清, 张永林. 高速分件供送螺杆的模态分析[J]. 包装工程, 2014, 35(3): 69-73. [17] KARABOGA D, BASTURK B. On the performance of artif-icial bee colony (ABC) algorithm[J]. Applied Soft Computing, 2008, 8(1): 687-697. [18] 毕晓君, 王艳娇. 约束多目标人工蜂群算法[J]. 吉林大学学报: 工学版, 2013, 42(2): 397-403. Optimization of high speed variable pitchtiming screw based on artificial bee colony algorithm LI Quan-lai (School of Materials Science and Mechanical Engineering, Beijing Technology and Business University, Beijing 100048, China) 10.13652/j.issn.1003-5788.2017.08.015 北京市教育委员会科技发展计划面上项目(编号:KM201510011005);北京工商大学两科基金培育项目(编号:19008001273) 李全来(1982—),男,北京工商大学讲师,博士。 E-mail: liquanlai@th.btbu.edu.cn 2017—02—07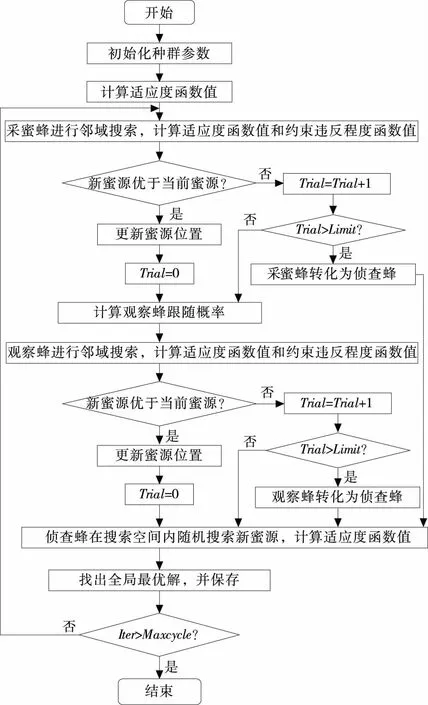
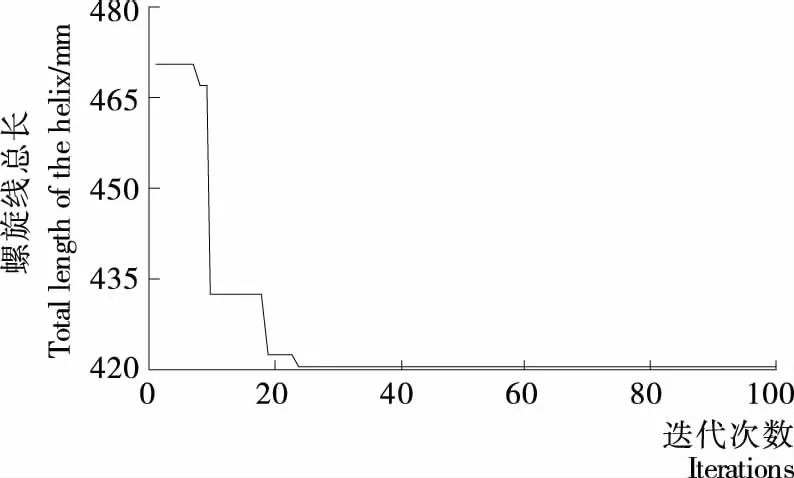
3 优化结果及分析
4 结论