巧做平行线求解一类“基底线性表示”问题

福建省泉州市泉州培元中学 张 琪

巧做平行线求解一类“基底线性表示”问题

福建省泉州市泉州培元中学 张 琪

向量兼有“数”和“形”的特点，有与数的运算不同的运算系统，加上其本身具有的几何特征，因此向量解题灵活多变，正因为如此，向量这一好用的工具却反成了学生学习的绊脚石。

【试题再现】

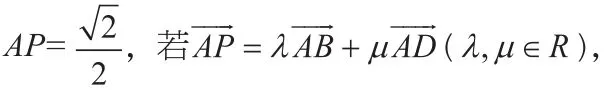
一、问题的提出

笔者在课上用该解答讲解后，较多学生反映该解答较难想到。其实涉及考查向量基底表示的这类问题，学生普遍觉得比较难，但这类题目所求的往往是基底表示的系数的值，因此我们换种角度思考，是否可以不分别求出 的值，而把当成一个整体把值求出来？

先来看我们熟悉的一个命题：

根据该结论，我们知道只要点C在AB直线上，我们不需要计算的值，就可知为1。

借助该结论，我们可以得到如下推论： 点C是△ 所在平面上的一点，若过点C做直线AB的平行线交直线OA，OB于 两点，其中，则

图1

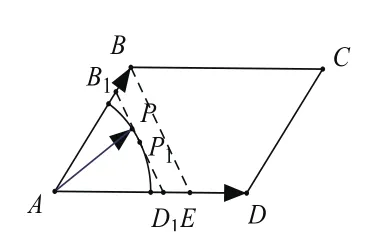
图2

方法总结：求“基底线性表示的系数和”这类考题，我们通过做平行线可把求的值转化为△ 与△ 的相似比的问题。

二、问题的解决

三、推论应用

图3

例2 如图4，△ 与△ 的面积之比为2∶1，点P是区域ABDC内任意一点（含边界），且

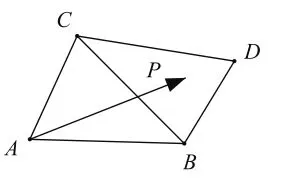
图4

例题解析：

例1 如图5，连接AB，过点C作AB的平行线 交OA延长线于 ，可知解得则

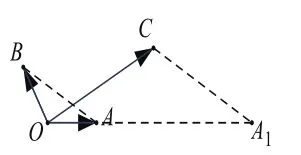
图5

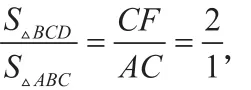
图6

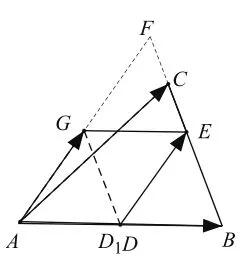
图7

供人以鱼，只解一餐，授人以渔，终身受用，我们在介绍方法的同时，应该尽量促使学生以探索者的身份去发现问题，总结规律，获得成功，激发学生学习的内生动力。