拓展直觉思维空间 提高学生解题能力

湖南省益阳市第一中学 胡进文

拓展直觉思维空间 提高学生解题能力

湖南省益阳市第一中学 胡进文

在数学教学中，学生常常提到这样的问题：“这种方法你是怎么想到的？我为什么想不到?”回答很简单：“凭直觉。”“直觉是从哪里来的？”这个问题是很难回答的。实际上，解数学问题最初往往是凭直觉，而直觉思维是指人们凭借已有知识组块和解题经验通过观察、分析快速发现解决问题的方式或途径的一种思维方式。而学生所提出的问题，说明了他们解题时缺少直觉思维的素材。因此，要提高学生的解题能力，我们必须拓展学生直觉思维的空间。拓展学生直觉思维空间的面较广，本文仅从三个方面谈谈如何拓展学生直觉思维的空间。

拓展；直觉；思维空间；提高；解题能力

一、结构联想

灵活的、精巧的解题技巧不会凭空出现，它是在由此及彼的联想中迸发出来的。教学中，我们要不失时机地鼓励学生联想，寻找问题的内在规律。联想的方式很多，下面谈谈通过联想问题的结构来拓展学生直觉思维的空间。

数学大师波利亚曾经说过：“你以前见过它吗？你是否见过相同的问题而形式稍有不同？”所谓结构联想，就是发现问题的结构像什么，就联想什么。

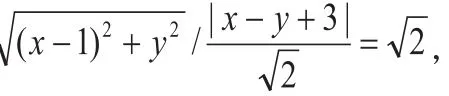
指导学生联想，若问题中出现了二次根式或绝对值，都可以联想距离公式。

二、一题多思，挖掘“副产品”

一题多思能有效训练学生的发散思维，同时，我们还能发现题目的“副产品”，这也是拓展学生直觉思维空间的有效手段之一。

例5 过抛物线 的焦点的一条直线与抛物线相交的两个交点的纵坐标为y1、y2，求证：y1y2=-p2。

讲完这道题后，我们不能就此罢手，还应引导学生继续探索，看看还有多少结论，还有多少“副产品”（如图1）：

（1）∠CFD=90°；

（2）∠ANB=90°， ∠CFD=90°(M、N为中点)；

（3）NF⊥AB；

（4）AN⊥FC，BN⊥FD；

（5）|KF|2=|CK|·|DK|；

（6）A、O、D（B、O、C）三点共线；

（7）以AB为直径的圆与准线相切；

（8）CF∥BN ；

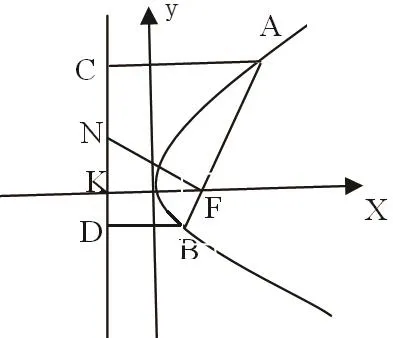
图1

（11）kOA．kOB=-4；

通过这样的训练，学生在今后的解题中kOA·kOB遇到了抛物线焦点弦的问题，很自然地联想到以上结论，这正是我们拓展学生直觉思维空间的好方法。

三、归纳性质，形成知识组块

教师最感棘手的问题是教学时间不够，学生解题速度慢或想不出来，关键还是学生大脑里储存的信息量少。要解决好这个问题，教师要引导学生从一类题中发现其共同性质，形成知识组块，拓展学生直觉思维的空间。

（1）椭圆上的点与两焦点的张角，以短轴端点向两焦点所张的角最大；

（2）椭圆上的点与长轴两端点的张角，以短轴端点向长轴两端点所张的角最大；

（3）如图2：

①AB∥OP；

②P点在x 轴上的射影为焦点F；

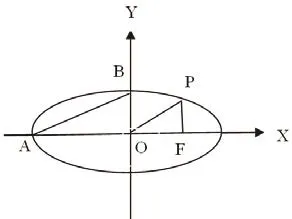
图2

总之，直觉所运用的“知识组块”是经验的积累和升华。古人云：站得高，看得远。学生大脑里储存的知识组块多，审题的高度站得高，解题的思维速度加快，这对提高学生的解题能力大有裨益。

[1]王秀彩，顾岚.三角函数的图象与性质[J].中学数学教学参考，2016（Z1）．