机电集成形状记忆合金活齿传动装置受力分析
柴宗兴 许立忠
燕山大学机械工程学院,秦皇岛,066004
机电集成形状记忆合金活齿传动装置受力分析
柴宗兴 许立忠
燕山大学机械工程学院,秦皇岛,066004
为了研究机电集成形状记忆合金(SMA)活齿传动装置的受力规律,采用电流直接加热方式并基于Brinson的一维本构模型,推导出装置中SMA的驱动方程;通过活齿传动装置受力分析,建立了装置的耦合力学方程,绘出了装置参数变化时活齿受力随输出轴转角变化曲线和不同输入电流下输出特性曲线,得到了装置参数变化对活齿受力的影响规律和输入电流对装置输出特性的影响规律。研究结果为装置的进一步优化和动力学研究提供了参考,为样机的制作和试验提供了依据。
形状记忆合金; 活齿传动; 多场耦合; 受力分析; 输出特性
Abstract:In order to study the force laws of a movable teeth transmission integrated with SMAs, using direct current heating method and one-dimensional constitutive model of Brinson ,the driving equations of the SMA in the transmission were derived. Through the force analysis of the movable gear transmission, the coupling force equations of the transmission were established. The force curves of the movable tooth with the output shaft angles were plotted when the device parameters were changed,and the output curves were plotted under different input currents. The influences of the parameters on the force in the the movable tooth and the output curve under the input current were obtained.The results provide a theoretical basis for the further optimization and dynamics of the system, and provide the basis for the prototype manufactures and tests.
Keywords:shape memory alloy (SMA); movable teeth transmission; many field coupling; force analysis; output characteristics
0 引言
当前国内外常采用的智能驱动方式有压电驱动、磁致伸缩驱动和形状记忆合金(SMA)驱动三类。与压电材料和磁致伸缩材料比较,SMA的能量密度最高,同时也具有较高的驱动频率和较大的应力应变,综合性能突出[1]。SMA在航空航天、微型机器人、精密仪器仪表、生物工程、医学工程等领域均有广阔的应用前景。
SMA驱动器可分为直线式和旋转式。目前国内外大部分采用直线式。何存富等[2]提出了预拉伸的SMA丝扭力圆管驱动。刘颖等[3]利用SMA的记忆特性设计了一种低转速可连续旋转的电机。李贺等[4]提出了一种基于SMA与电机混合驱动的电机。吴佳俊等[5]提出了一种可实现正反两向扭转的SMA驱动器。HWANG[6]设计出由三根SMA丝驱动,以渐开线齿轮为传动的旋转驱动器。SMA驱动的旋转驱动器鲜有报道。
本文提出了机电集成SMA活齿传动装置。该装置利用活齿传动把SMA的拉伸变形转化为激波器的行波运动,从而转化为输出轴的旋转运动。该装置具有结构简单、体积小和低转速等优点。活齿传动作为一种重要传动机构,一直受到科技工作者的广泛关注。李瑰贤等[7]对滚柱活齿传动进行了受力研究;李剑锋等[8]研究了一种采用凸轮激波的滚动活齿传动;李怀勇等[9]、李冲[10]研究了新型压电电机中活齿传动规律; YI 等[11]研究了一种新型纯滚动活齿传动。机电集成SMA活齿传动装置的受力分析是该种传动装置设计、分析和性能控制的重要基础,目前研究仍处于空白阶段。本文通过建立该传动装置的力学方程,得出活齿受力随输出轴转角变化的规律、基本参数变化对活齿受力的影响及输入电流对装置输出特性的影响。
1 基本结构及工作原理
机电集成SMA活齿传动装置主要由驱动和传动两部分组成,其结构如图1所示。驱动部分由一对互成90°的SMA丝和一对互成90°的偏置弹簧组成。传动部分是由激波器、活齿、活齿架和中心轮组成的活齿传动,其中活齿架与输出轴固连,中心轮与机架外壳固连。
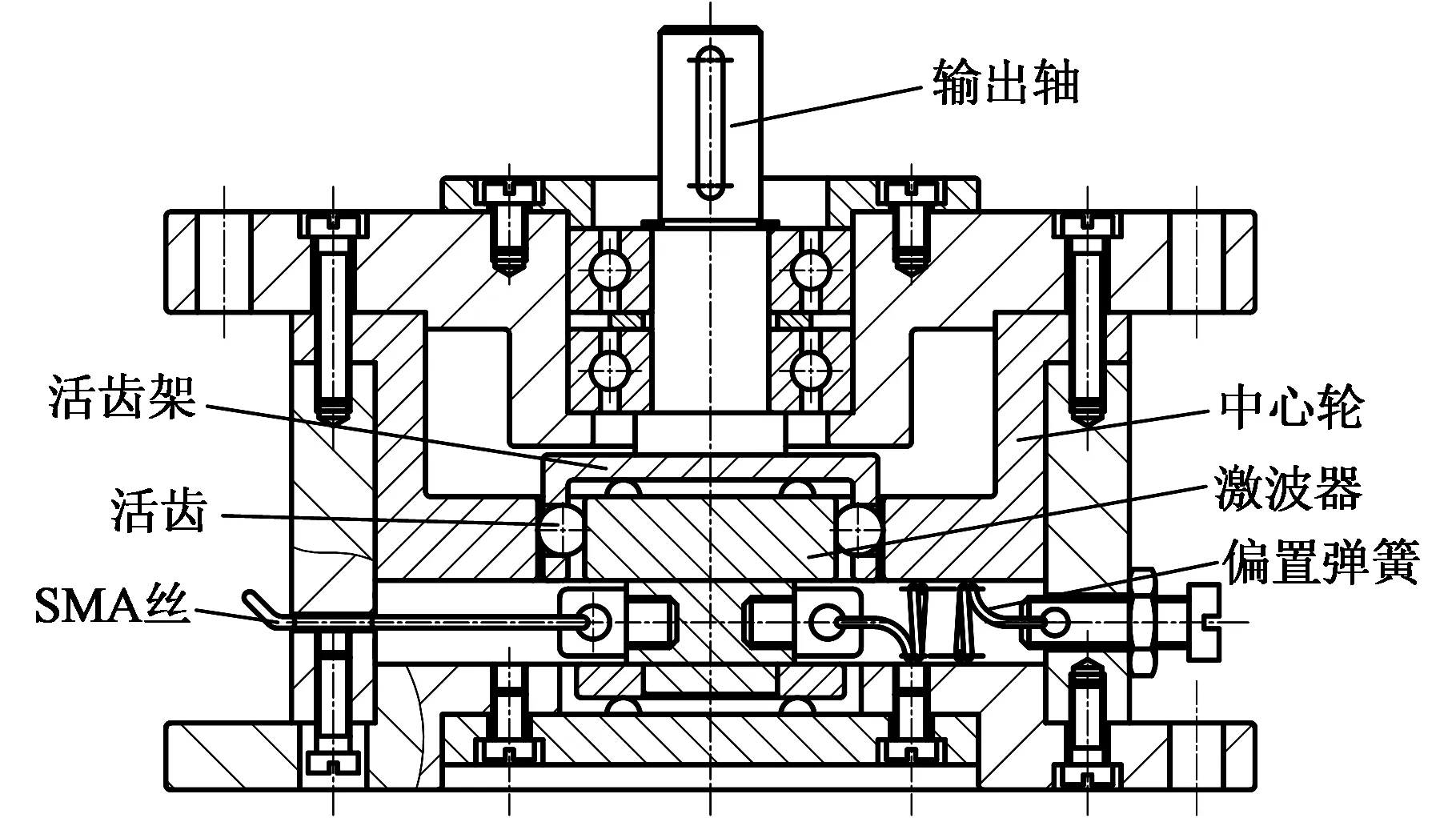
图1 机电集成SMA活齿传动装置组装图Fig.1 The assembly diagram of the movable teeth transmission integrated with shape memory alloys
工作时,给一侧的SMA丝通电,SMA丝温度升高,发生马氏体逆相变,产生形变克服弹簧力恢复变形前形状,拉动激波器运动;当不通电时,SMA丝逐渐冷却,在弹簧作用下产生变形,同时拉动激波器运动。从而激波器形成一个往复振动过程。同理,电信号作用在另一侧SMA丝上时,激波器也形成一个往复振动过程。激波器在两个垂直方向上往复振动的叠加,使激波器绕固定的中心做行波运动。激波器激发活齿转动,使固连活齿架的输出轴转动输出扭矩。
2 静力学方程的建立
图2所示为单根SMA丝驱动简化模型。在加热前,SMA组织结构全为非孪晶马氏体。选取驱动应力σL=σf=210 MPa。

(a)加热过程 (b)冷却过程图2 SMA驱动简化模型Fig.2 SMA drive simplified model
当加热升温满足逆相变条件
时,SMA发生马氏体逆相变过程,由于T>TAs,由Brinson模型中相变方程可知[12]:

(1)

马氏体逆相变一维本构方程为
(2)
式中,EM、EA分别为SMA在马氏体、奥氏体状态下的弹性模量;ε为应变;σ为应力;εmax为最大相变应变;ρ为密度;Δμ0为相对初始温度下内能的变化量;Δη0为相对初始温度下熵的变化量;σas为T>TMs时奥氏体相变开始临界应力;σaf为T>TMs时奥氏体相变结束临界应力;TMs为马氏体相变开始温度;εas、εaf分别为σas、σaf对应的弹性应变。
表1所示为本文选用SMA材料的参数取值。

表1 SMA材料参数表Tab.1 The parameters of SMA
将σL=σf和表1中相关参数代入马氏体逆相变一维本构方程相应应变得εL=0.04875。
当满足正相变条件
时,SMA发生马氏体正相变。由于T>TMs,由Brinson模型中相变方程可知[7]:

(3)
式中,σs为T 激波器几何中心运动到另一端时,SMA丝的应变 εH=εL-εa (4) 设工作驱动力为W,则有 (5) 驱动过程中应力应变的驱动斜率关系为 (6) 则驱动路径中应力应变关系为 (7) 由于SMA丝的表面积和质量都很小,辐射换热量和相变潜热远小于加热所产生的热量,二者可忽略不计,则SMA热效应方程为 (8) 式中,c为SMA的定压质量热容,其值为7.14J/(kg·K);ρR为SMA丝的平均电阻率[13],取为0.8×10-6Ω·m;I为SMA的加热电流;S为SMA丝的换热面积;h为自然条件下,对流换热表面传热系数,为5W/(m2·K);m为SMA丝的质量;d为SMA直径;Tf为流体温度,一般情况下,可认为与环境温度近似相等;T1为SMA相变的初始温度;t为加热时间。 SMA驱动的受力如图3所示。偏置弹簧的变形量与SMA丝的形变量关系为 (9) 式中,ε1、ε2分别为X轴和Y轴SMA丝的应变;L3、L4分别为X轴和Y轴偏置弹簧的伸长量。 图3 SMA驱动受力图Fig.3 The force diagram of SMA drive 如图3所示,对X轴和Y轴SMA丝驱动进行受力分析,可得 (10) SMA驱动对激波器的作用合力为 (11) 活齿传动中激波器的受力分析如图4所示。 图4 激波器受力图Fig.4 The force diagram of wave generator 以激波器为研究对象,列平衡式: (12) θ=2π/zG 式中,θ为相邻两个活齿间夹角;Fjmax为激波器对活齿的最大作用力;Fji为激波器对活齿i的作用力;zG为活齿数。 假设只有激波器变形,活齿和中心轮不变形,在驱动力F的作用下,激波器沿径向的最大位移为δjmax,此时每个活齿的径向位移为 δji=δjmaxcos(iθ) (13) 根据赫兹理论,活齿和激波器啮合副间各接触点变形与二者间相互作用力Fji间的关系[14]为 (14) 式中,KH为赫兹接触刚度。 联立式(12)~式(14)得 (15) 本装置采用中心轮齿数zK=14,活齿数zG=15的活齿传动,则有传动比 i12=zG/(zG-zK)=15 每个活齿在转动过程中可以转动到其他活齿的位置,为使研究问题得以简化,以第i个活齿为研究对象来代替其他所有活齿转动[15]。忽略传动过程中的摩擦及装配误差,则第i个活齿的受力如图5所示。图中,R为激波器半径,r为活齿半径。 以第i个活齿球心O2、激波器的圆心A和中心轮轨迹的几何中心O三点共线位置(即O1、A1和O三点共线)为Y轴,建立图5所示坐标系。已知当激波器转过φ1角时,第i个活齿随活齿架转过φ2角,则传动比i12=φ1/φ2。通过分析可知,活齿架每转过π/210 角度时,就会有一个活齿与中心轮齿廓的齿顶相切。转过π/105角度时,就会有一个活齿退出啮合。 对第i个活齿列受力平衡方程: (16) 式中,Fsi为活齿架作用在第i号活齿上的力;Fgi为中心轮作用在第i号活齿上的力。 图5 活齿受力图Fig.5 The force diagram of movable teeth 忽略传动过程中间隙,且只考虑激波器与圆柱活齿接触的弹性变形,则在驱动力作用下,当激波器转过微小角度Δθ时,活齿与激波器间接触处产生的弹性变形为[16] 式中,ε为活齿对激波器造成的最大弹性变形。 假设活齿与激波器间作用力与激波器变形量成正比,则有 (17) 由转矩的定义可得装置的输出转矩: (18) 式中,Si为第i号活齿的向径。 联立式(1)~式(3)、式(7)、式(8)、式(10)、式(11)、式(15)~式(17),装置的耦合静力学方程为 选取X轴SMA丝电流 式中,n为自然数。 进行加热,其中Y轴方向电流比X轴滞后1 s,其电流曲线如图6所示。装置的基本参数如表2所示,代入装置的耦合静力学方程,则SMA温度曲线如图7所示。以刚开始进入啮合区域的活齿为研究对象,激波器转过2π为例进行求解。绘制活齿受力曲线,如图8所示。 由图8可得如下结论: (1)当输出轴转角为0(激波器转角为0)时,刚进入啮合区域的活齿恰好处于受力的临界点; (2)当输出轴转到π/30(即激波器转角为π/2)时,活齿受到来自激波器、中心轮和活齿架的力均达到最大值; 图6 电流I1曲线Fig.6 The curve of current I1 参数数值参数数值d(mm)0.3zK14L0(mm)20a(mm)0.2K(N/mm)10.6R(mm)7.5L'0(mm)2.6r(mm)1.5zG15 图7 温度θw曲线Fig.7 The curve of temperature θw 图8 活齿受力曲线Fig.8 The curve of forces on movable teeth (3)当输出轴转到π/14(即运动到中心轮齿顶)时,活齿所受激波器的力为0(即不参与啮合); (4)活齿在传动过程中,中心轮对活齿的作用力Fgi最大,其次是激波器对活齿的作用力Fji,活齿架对活齿的作用力Fsi最小。 不改变SMA的输入电流和冷却方式,只改变装置的相关参数,可得一系列装置参数对活齿受力的影响。图9~图12所示分别是 SMA丝直径d、激波器偏心距a、活齿半径r和激波器半径R变化对活齿受力的影响。 由图9~图12可得: (1)随着SMA丝直径d的增大,活齿受力Fji、Fsi和Fgi均随之增大,其中对Fgi影响最为显著,对Fsi影响最小; (2)随着激波器偏心距a的增大,活齿受力Fji、Fsi和Fgi均随之增大,其中对Fsi影响最为显著,对Fji影响最小; (3)随着活齿半径r的增大,活齿受力Fgi随之增大,活齿受力Fji和Fsi随之减小,但变化均不显著; (4)随着激波器半径R的增大,活齿受力Fji、Fsi和Fgi均随之减小,其中对Fsi影响最大,对Fji影响最小,但变化均不显著; (5)当输出轴转角在0~π/14角度范围内变化时,随着输出轴转角增大,同一参数变化对活齿受力影响显著增强;当输出轴转到π/30时,同一参数变化对活齿受力影响达到最大;之后随着转角增大,同一参数变化对活齿受力影响又逐渐减小。 分别选取SMA输入电流I1、I2和I3进行加热,Y轴方向电流比X轴滞后1/4周期,其电流曲线如图6、图13和图14所示。其中IX2、IY2的幅值分别为15.16 mA和13.975 mA,周期为3.2 s,冷却方式采用吹冷风的强制冷却,对流换热表面传热系数为6.3 W/(m2·K);IX3、IY3的幅值分别为19.41 mA和17.89 mA,周期为2 s,冷却方式仍采用强制冷却,对流换热表面传热系数为10.32 W/(m2·K)。分别把输入电流I1、I2、I3及相应的冷却参数和表2中装置的基本参数代入静力学方程和输出转矩式(18),可得SMA输入电流对装置输出转矩的影响曲线,如图15所示。 (a)Fji曲线 (b)Fsi曲线 (c)Fgi曲线图9 SMA丝直径d变化对活齿受力的影响Fig.9 The effects of don stress of movable tooth (a)Fji曲线 (b)Fsi曲线 (c)Fgi曲线图10 激波器偏心距a变化对活齿受力的影响Fig.10 The effects of a on stress of movable tooth (a)Fji曲线 (b)Fsi曲线 (c)Fgi曲线图11 活齿半径r变化对活齿受力的影响Fig.11 The effects of r on stress of movable tooth (a)Fji曲线 (b)Fsi曲线 (c)Fgi曲线图12 激波器半径R变化对活齿受力的影响Fig.12 The effects of R on stress of movable tooth 图13 电流I2曲线Fig.13 The curve of current I2 图14 电流I3曲线Fig.14 The curve of current I3 (a)随时间变化 (b)随输出转角变化图15 输入电流对输出转矩的影响曲线Fig.15 The effects of input current on the output torque 由图15可得:当SMA输入电流I增大时,输出转矩随时间变化的周期缩短,即装置的输出转速随电流的增大而增大,但对输出转矩随输出转角变化无影响。 (1)中心轮受力最大,最易出现磨损现象,在活齿传动装置实际设计中应优先考虑中心轮材料的力学性能。 (2)SMA丝直径和激波器偏心距对活齿受力影响较大,若想改变装置中受力情况,应主要考虑改变SMA丝直径和激波器偏心距两个参数。 (3)活齿受力与SMA丝直径、激波器偏心距成正相关,与激波器半径成负相关;中心轮作用在活齿上的力与活齿半径成正相关,激波器作用在活齿上的力和活齿架作用在活齿上的力与活齿半径成负相关。 (4)当X轴和Y轴两相输入电流相差1/4周期时,SMA输入电流只影响输出转速,导致输出转矩随时间变化的周期缩短,而对任一转角位置的输出转矩无影响。 [1] 闫晓军,张小勇. 形状记忆合金智能结构[M]. 北京:科学出版社, 2015:3-4. YAN Xiaojun, ZHANG Xiaoyong. Shape Memory Alloy Smart Structure[M]. Beijing: Science Press, 2015:3-4. [2] 何存富, 金江, 陶宝祺. 形状记忆合金驱动薄壁圆管扭转变形分析及试验研究[J]. 机械工程学报,2001,37(2):17-21. HE Cunfu, JIN Jiang, TAO Baoqi. Analysis and Experimental Study on Torsional Deformation of Thin Walled Tubes Driven by Shape Memory Alloy [J]. Journal of Mechanical Engineering,2001,37(2):17-21. [3] 刘颖, 闫晓军. 一种低速连续旋转SMA电机的设计与试验[J]. 航空动力学报, 2010, 25(9):2023-2029. LIU Ying, YAN Xiaojun. Design and Experiment of a Low Speed Continuous Rotary SMA Motor[J]. Journal of Aeronautics and Astronautics,2010,25(9):2023-2029. [4] 李贺, 董二宝, 许旻,等. 基于SMA的混合驱动器设计[J]. 机电一体化, 2011,17(4):56-59. LI He, DONG Erbao, XU Min, et al. Based on SMA Hybrid Drive Design [J]. Mechanical and Electrical Integration,2011,17(4):56-59. [5] 吴佳俊, 王帮峰, 芦吉云,等.一种形状记忆合金扭转驱动器的制备与测试[J].中国机械工程,2014,25(12):1591-1594. WU Jiajun, WANG Bangfeng, LU Jiyun, et al. The Preparation and Testing of a Shape Memory Alloy Reverse Drive [J]. China Mechanical Engineering,2014,25(12):1591-1594. [6] HWANG D. A Rotary Actuator Using Shape Memory Alloy (SMA) Wires[J]. Transactions on Mechatronics,2014,19(5):1625-1635. [7] 李瑰贤, 杨伟君, 顾晓华. 滚柱活齿传动受力分析的研究[J]. 机械设计,2002,19(1):34-36. LI Guixian, YANG Weijun, GU Xiaohua. Roller Movable Teeth Transmission Force Analysis Research [J]. Journal of Mechanical Design, 2002,19(1):34-36. [8] 李剑锋, 董新蕊. 凸轮激波滚动活齿传动啮合力分析方法[J]. 机械工程学报,2008,44(5):39-44. LI Jianfeng, DONG Xinrui. The CAM Roller Movable Teeth Transmission Meshing Shock Force Analysis Method [J]. Journal of Mechanical Engineering,2008,44(5):39-44. [9] 李怀勇, 许立忠. 杆式压电电机传动系统中的活齿受力分析[J]. 工程力学,2014,31(1):201-208. LI Huaiyong, XU Lizhong. Bar Type Piezoelectric Motor Drive System of Movable Tooth Stress Analysis [J]. Journal of Engineering Mechanics,2014,31(1):201-208. [10] 李冲. 机电集成压电谐波传动系统研究[D]. 秦皇岛:燕山大学,2016. LI Chong. Mechanical and Electrical Integration of Piezoelectric Harmonic Drive System Research [D]. Qinhuangdao: Yanshan University,2016. [11] YI Y, JI Y. Force Analysis for Pure Rolling Movable Teeth Transmission [C]// International Conference on Advanced Electronic Science and Technology. Shenzhen,2016:987-992. [12] BRINSON L C. One-dimensional Constitutive Behavior of Shape Memory Alloys: Thermomechanical Derivation with Non-constant Material Functions and Redefined Martensite Internal Variable[J]. Journal of Intelligent Material Systems & Structures,1993,4(2):729-742. [13] 杨杰,吴月华. 形状记忆合金及其应用[M]. 合肥:中国科学技术大学出版社,1993:109. YANG Jie, WU Yuehua. Shape Memory Alloy and Its Application [M]. Hefei: University of Science and Technology of China Press,1993:109. [14] 曾强, 李鹏, 陈兵奎. 空间凸轮活齿传动的应力变形分析[J]. 机械工程师,2004(10):59-62. ZENG Qiang, LI Peng, CHEN Bingkui. The Deformation and Stress of the Spatial CAM Movable Teeth Transmission Analysis [J]. Mechanical Engineers,2004(10):59-62. [15] 李怀勇. 新型杆式压电电机研究[D]. 秦皇岛:燕山大学,2013. LI Huaiyong. New Bar Type Piezoelectric Motor Research [D]. Qinhuangdao: Yanshan University, 2013. [16] 丁肇棣, 曲继方. 波齿传动的受力分析和效率计算[J]. 燕山大学学报,1988(2):31-35. DING Zhaodi, QU Jifang. Force Analysis and Efficiency Calculation of Wave Gear Transmission [J]. Journal of Yanshan University,1988(2):31-35. (编辑袁兴玲) ForceAnalysisoftheMovableTeethTransmissionIntegratedwithSMAs CHAI Zongxing XU Lizhong School of Mechanical Engineering, Yanshan University, Qinhuangdao, Hebei,066004 TH122 10.3969/j.issn.1004-132X.2017.19.011 2016-11-21 2017学年燕山大学硕士研究生创新项目(2017XJSS012) 柴宗兴,男,1992年生。燕山大学机械工程学院硕士研究生。主要研究方向为机电集成SMA活齿传动系统。许立忠(通信作者),男,1962年生。燕山大学机械工程学院教授、博士研究生导师。

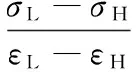











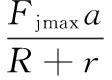

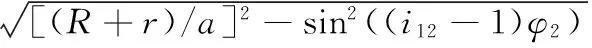
3 算例的求解与分析
3.1 活齿受力分析




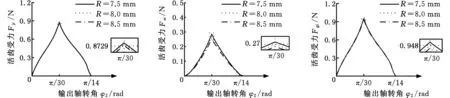
3.2 装置参数对活齿受力影响
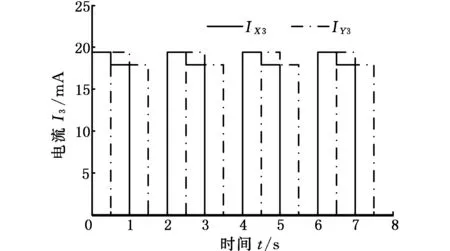
3.3 SMA输入电流对输出特性的影响






4 结论

