挖掘隐含信息 准确解决物理问题

王宴兵

挖掘隐含信息 准确解决物理问题

王宴兵

有效审题是解题的先决条件，很多学生缺乏审题意识，随意看了一下就开始做，往往事倍功半。很多物理题目条件给出很隐晦，如果不仔细挖掘，联系已知整体分析，提炼出有用信息，就很难理解出题者用意，无法顺利解题。或者在解题时不能兼顾所有限制条件，就会使得解题思路出现漏洞，不能得到完美解题。因此，教会学生如何发掘隐含条件十分重要，这直接关系到解题的正确与否以及得分，对学生的物理成绩有很大影响。

高中物理；隐含条件；解题

一、 挖掘物理题目

题目的隐含信息往往存在于一个或几个词语中，这些词语在教学时我们要提醒学生留意，比如“恰好”“最大”等，往往这些信息都会给解题带来感悟，列出几个方程，成为解题的关键。对于题目挖掘的掌握在于日常训练中培养学生对这些词语的敏感度，学生对这些词语形成条件反射后，那么就不会轻易错过重要的信息。另外我们也要注意对学生基本功的培养，这样学生才能利用好这些有用的信息。

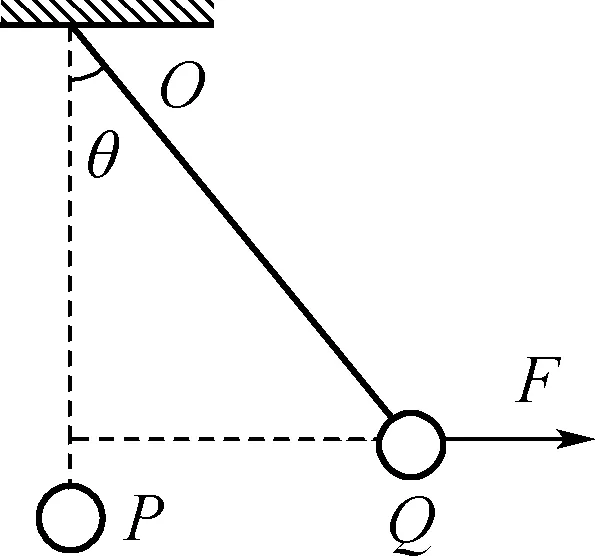
图1

例：如图，有一个质量为m的小球，用一根长度为L的轻绳悬挂在O点，此时若给小球一个外力，大小为F，方向水平向右，使小球从平衡位置P点十分缓慢地移动到Q点，此时轻绳与竖直方向的夹角为θ，那么在此过程中外力做的功是

( )

A.mgLcosθB.mgL(1-cosθ)

C.FLsinθD.FLθ

此题要注意的一点是题目中的“缓慢”“轻绳”二字，“缓慢”二字包含很多信息，说明小球一直处于平衡状态，“轻绳”二字说明绳子的质量忽略不计，在小球运动过程中外力一直处于水平状态，而小球的受力状况一直在改变，因此外力是一个变力，所以不能直接用功的公式求解，要注意转化，在此过程中小球的能量守恒，因此外力做的功都是在克服小球重力做功，因此外力的总功就是小球重力势能的增加量，通过对小球进行受力分析，再结合数学知识可以得出WF=mgL(1-cosθ)。

其实有关于平衡状态的判断有很多种，除了缓慢运动，还有匀速运动，在阅读题目时学生要留意题目中的字眼，这些往往是解题的关键。通过这些条件我们才可以列出物理方程，获得解题思路，进而顺利解题。

二、 挖掘物理情境

物理题目大多来源于生活，引用现象时总会忽略一些生活中不必要的因素。对此，在阅读题目时要注重实际情境的分析，比如有一些题目提到“光滑平面”“质量很小的粒子”等等，往往都是一句话带过，学生也是一眼掠过，在解题时总觉得题目缺少信息而被阻挠，无法快速解题。挖掘隐含在物理情境中的条件有助于学生更好地分析题目，从而确定解题思路、准确解题。

例：如图2所示，在光滑的水平桌面上有一个斜劈a，其斜面光滑，在斜面的顶端有一物体b，在物体b下滑的过程中，b受到a的弹力对b做功为W1，b对a的弹力对a做功为W2，则下列关系正确的是

( )

A.W1=0，W2=0 B.W1≠0，W2=0

C.W1=0，W2≠0 D.W1≠0，W2≠0

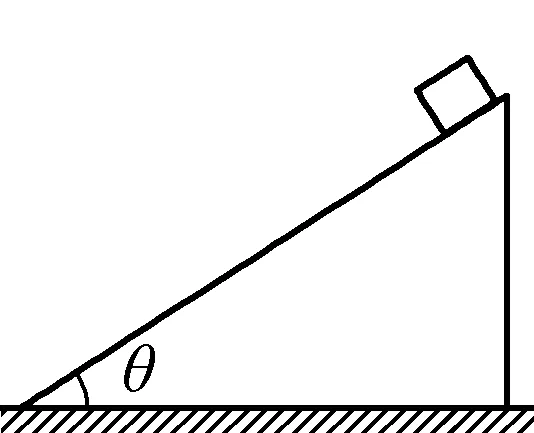
图2

图3

本题学生最容易错选C，因为物体b受到的力与它的运动方向垂直，这是因为学生忽略了斜劈放置在光滑水平面上，所以物体b运动时，斜劈也会在水平面运动，因此正确答案应该是D，W1，W2均不为零。整个运动过程如图3所示，斜劈会在弹力作用下沿水平方向向右运动。在受力分析时先个体再整体，会发现在以整体进行受力分析时，有了合外力，因此整个系统会运动，做功的力为a和b之间的弹力。

题目会给学生设置很多物理情境，学生要学会发掘这些情境下的物理条件加以利用，这样才不会掉进题目陷阱，盲目解题。

三、 挖掘物理过程

物理过程的研究不可避免会涉及很多物理状态，这些物理状态通过特定方式连接就形成了一个复杂的物理过程。在考试时，物理过程的分析需要学生先分析各个物理状态，将各个分析结果相连在一起整合为解题思路。其关键在于在各个物理状态的衔接处会有条件限制，了解了各个物理状态的特点之后，只有找出它们潜在的交叉联系，才能准确找到题目的隐含信息，从而准确解题。

图4

例：如图4，一个质量为m的物体放在一个传送带的A点上，此传送带以速度v匀速运动，大小为2 m/s，且传送带的长度AB=4 m，已知物体与皮带之间的摩擦系数为0.2，则物体运动到点B的时间是

( )

A. 2 s B. 2.5 s

C. 4 s D. 无法确定

此题的隐含条件在于物体的运动过程，物体的运动状态需要学生逐点分析，发掘物体正确的运动过程，学生很容易错选A项，这是因为学生没有认真分析整个运动过程，以为一直在做匀加速运动，实际情况是物体先做匀加速运动，再做匀速运动，经过计算易得B项才是正确选项。题目中的运动状态判定需要计算，当学生遇到这类型题目时一定要有一种意识——此题可能有几种运动状态，然后去求证是否有多个过程。如果不深入挖掘过程信息，势必会造成错解。

大多数物理过程不是很明显，学生一眼看不出来，这就需要其具备一定的质疑意识，不断分析、挖掘，注重经验积累，形成系统认知，以此做到熟能生巧，提高解题效率。

物理题目虽然简短，但是一字一句都有其作用，不会多余出现，因此我们要教会学生发掘题目，从题目出发，找到最合适的解题思路，正确快速解题。

王宴兵，云南省红河州第一中学。