基于最佳均匀扩散矩阵的物理层安全编码

杨 勇

(1.中国电子科技集团公司航天信息应用技术重点实验室，河北 石家庄 050081； 2.中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

基于最佳均匀扩散矩阵的物理层安全编码

杨 勇1,2

(1.中国电子科技集团公司航天信息应用技术重点实验室，河北 石家庄 050081； 2.中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

一定密度的均匀扩散矩阵是缩小物理层编码安全间隙的关键，针对如何构造这种最佳扩散矩阵进行了深入研究，设计了一种可以构造出任意规格、任意密度且均匀分布的、可逆扩散矩阵的算法。实验分析证明，针对任意规格的矩阵，该算法都可以方便、快捷地构造出任意密度、且均匀可逆的扩散矩阵。通过仿真分析发现，该算法构造的矩阵不但可以有效实现信道误码的扩散，达到缩小安全间隙的目的，而且与同类算法相比，该算法表现出了更好的性能。

物理层安全；扩散矩阵；安全间隙；安全编码

AbstractThe key to narrow the security gap is to find a diffusion matrix of even density,this paper deeply studies how to construct this kind of matrix,and then creates this algorithm which can construct any size,any density uniformly distributed and invertible diffusion matrix.Through the experimental analysis,this algorithm can easily construct any size matrix of this kind.Through simulation analysis,this algorithm not only realizes the diffusion of the channel code and narrows the security gap,but also has better performance compared with similar algorithms.

Keywordsphysical layer security;diffusion matrix;security gap;security code

0 引言

经典的安全发生在通信协议高层，由各种加密算法实施信息安全的保护。计算复杂度是这些高层加密算法的安全基础，只有在攻击者计算能力是多项式时间的前提下，它们才是安全的。不同于高层加密算法，物理层安全是信息论意义上的安全，它依靠合法通信者与非法通信者之间信道质量的差异实现信息的安全保护，这是一种不依赖计算能力的绝对意义上的安全性。

物理层安全研究的核心是安全编码，而如何缩小安全间隙是安全编码主要考虑的问题之一。目前有很多种研究方案，其中公认最有效的是扩散矩阵，然而目前还没有找到简便、有效的方法构造扩散矩阵，这也成为解决缩小安全间隙的关键所在。本文针对扩散矩阵设计了一种简便算法，成功地解决了任意规格、密度均匀扩散矩阵的构造问题，从而达到了缩小安全间隙的目的，为设计安全编码提供了有力的支撑。

1 信道模型

安全和通信一直以来被看作2个完全不同的领域，1975年，贝尔实验室的Wyner基于物理层概念提出的窃听信道模型第一次把安全性和可靠性联系在了一起[1]。

Wyner信道模型如图1所示，合法通信者Alice和Bob相互通信，非法窃听者Eve通过窃听信道监听。在发射端，原始信息M经过信道编码处理后输出为C，C分别通过合法信道和窃听信道到达合法接收者Bob和非法窃听者Eve的接收端，由于合法信道和窃听信道的通信质量存在差异，C到达Bob端为CB，到达Eve端为CE[2]。

图1 Wyner信道模型

在理想情况下，因为信道编码的保护，可以假设Alice和Bob之间是无误码通信，而由于信道质量的差异，Alice和窃听者Eve之间却传递不了任何信息。这种理想的Wyner窃听信道模型用香农信息论公式表示为：

I(A、E)=H(A)-H(E|A)=0。

为了更形象地说明合法者与窃听者通信质量的差异，除了信息论公式也可以用误码率表示：在合法者Alice和窃听者Bob之间误码率近似为0，即Alice发送的信息Bob可以完整无误地收到，同时，Eve在窃听信道上的误码率趋近0.5，即什么信息也没有得到。

通过比较发现，经典加密与物理层安全编码的安全基础不同，二者在通信协议栈的位置也不一样。应该说，物理层安全更好地补充了经典加密算法，二者共存提供了更好的安全性[3]。

2 安全间隙

在理想的Wyner窃听信道模型中，当二者信道质量差异满足一定条件时，Alice和Bob之间的误码率为0，而Eve的误码率趋近0.5。在物理层安全中把满足这种要求的信道质量差异称为安全间隙，这个概念是由Klinc首先提出的[4]。

安全间隙如图2所示。窃听者信道的信噪比SNRE越低，误码率BERE越高，当到达SNRE_max时，BER趋近0.5；同时，合法者信道的信噪比SNRB高于窃听者，越高误码率越低，当高于SNRB_min时，误码率为0。如果Wyner模型能同时满足窃听者信道小于SNRE_max，合法者信道大于SNRB_min，那么就能实现在合法者无误码通信的同时，窃听者得不到任何信息。并把SNRE_max与SNRB_min之间的间隙称为安全间隙，间隙越小，差异化信道越容易实现，于是如何缩小安全间隙也就成为安全编码的一个重要研究方向[5]。

图2 安全间隙

从图2可以看出，缩小安全间隙的一个直观做法是得到更加陡峭的BER曲线，为了实现这个目的，Bladi[6]第一次使用了级联码结构，级联码示意图如图3所示。

图3 级联码示意

在级联码结构中，信道编码[7]是为了纠正合法者信道的突发错误，保证合法者无误码接收，预处理编码是为了扩大合法者信道的优势，保证在尽量小的安全间隙下窃听者得不到任何信息。

与本文相关的研究，在缩小安全间隙方面，Klinc等[8]提出了LDPC码删余方案[9]，在此基础上Wong等对LDPC码删余方案做了进一步研究[10]。随着研究的不断深入，不同学者发现信息拼接[11]、ARQ等技术手段[12]都可以在不同场景下达到缩小安全间隙的目的[13]。Kwark等从调制解调的角度提出了YARG码的概念[14]，通过调制映射最大化星座点间距缩小安全间隙。Baldi等第一次提出混乱编码的概念[15]，并指出当混乱矩阵‘1’元素的密度趋近0.5时，可以达到最佳效果，但是并没有给出具体的实现方法。在此之后相关学者进一步研究了混乱编码缩小安全间隙的方案[11,15]。在缩小安全间隙的所有方案中，混乱编码是公认的最佳方案，因此能否找到一种快速、有效的‘1’元素密度趋近0.5的混乱矩阵成为解决问题的关键。

3 均匀扩散矩阵

为了缩小合法者与非法者之间的安全间隙，使图2的曲线更加陡峭，要求预编码有更好的扩散能力。如图3所示，级联码模型的公式表示为：

C=m×S×G。

式中，m为信源信息；S为预处理编码；G为信道编码；C为编码后信息。假设信道编码G为一般的非系统码，且合法者有较好的信道，所以G总可以完全纠正信道误码，保证合法者的误码率为0，表达为：

m=C×G-1×S-1。

(1)

而非法者的信道质量差，依据安全编码的含义，在完成信道解码G-1后，由于不可能完全纠正信道误码一定会引入错误向量e，即

m×S+e=C′×G-1。

(2)

为了实现解码，继续在等式左、右两边乘以预编码逆矩阵S-1，即

m+e×S-1=C′×G-1×S-1。

(3)

由式(3)可知，信道解码G-1引入的错误向量e在右乘预编码逆矩阵S-1后，其作用相当于扩散错误向量e。理想情况下，无论错误向量e取何值，当右乘预编码逆矩阵后，都可以保证信源m的误码率趋近0.5。

为实现这一目标，预编码矩阵中元素‘1’的总体密度需要趋近0.5，并且在各列均匀分布。所以构造密度趋近0.5、均匀分布的可逆矩阵成为缩小安全间隙的关键。

下面以单位矩阵I(n)为基础，分析具体的构造过程：

步骤1 假设N为偶数(N为奇数原理相同)，从第2行到第N行随机选取(N/2)-1行，然后第1行依次与随机选取的(N/2)-1行分别相加。

步骤2 不包括第2行，从第1行及第3到第N行中，同样随机选取(N/2)-1行，使第2行依次与随机选取的(N/2)-1行分别相加。

步骤3 以此类推，第3行到第N行分别依次加到每次随机选取的(N/2)-1行上。最终得到的就是规格为N、可逆均匀、‘1’密度趋近0.5的矩阵。

步骤4 对得到的矩阵M实施基本行变换，并把相应的行变换作用到另一个单位矩阵I(n)，这样当原矩阵M变换成单位阵时，原单位阵I(n)变换成原矩阵M的逆矩阵M-1，完成逆矩阵的构造。M即上述预编码逆矩阵。

式(4)、式(5)和式(6)以规格为8的方阵为例，说明具体的变换过程，如下所示：

(4)

(5)

(6)

可逆性证明：因为I(n)是单位矩阵，在变换过程中只对I(n)做初等阵行变换，所以不改变可逆性，最终得到的矩阵M依然是可逆矩阵[16]。

密度证明：① 步骤1完成后，共进行了(N/2)-1次行加操作，第1列增加(N/2)-1个元素‘1’，加上第1行第1列的‘1’，共有N/2个‘1’，由此可知第1列‘1’的密度为0.5。

② 步骤2完成后，第2列元素‘1’的密度趋近0.5。与步骤1不同，这时第1列的元素也会随着第2列的行变换而发生变化，但密度趋近0.5不变，证明如下：

由于第1列元素‘1’随机分布，密度为0.5，那么步骤2随机选取的(N/2)-1行中有(N/4)-1个元素‘1’，或有(N/4)-1个元素‘0’是大概率事件；即使没有发生这种大概率事件，所选出‘1’或‘0’元素的数量也是以(N/2)-1为中心的正态分布，并且也可以证明最终行密度趋近0.5。

在上述大概率事件基础上，假设第2行第1列的元素为‘1’，且挑选出(N/4)-1个元素‘1’，那么在和第2行第1列元素‘1’做行加时，有(N/4)-1个元素‘1’变为元素‘0’，N/4个元素‘0’变为元素‘1’。此外，加上未挑选的(N/4)+1个元素‘1’，密度仍为0.5。基本的行变换公式为：

1+1=0； 1+0=1。

如果有(N/4)-1个元素‘0’，那么运算后元素‘1’有(N/4)+1个，可知密度趋近0.5。

如果假设执行步骤2时，第2行第1列的元素为‘0’，那么在步骤2做行变换时第1列的元素不发生变化，密度依然为0.5。

综上所述，在完成步骤2后，第1列、第2列的‘1’元素密度仍然等于或者趋近0.5。

③ 依次类推，在做完N步变换后，得到的矩阵是可逆的、且密度趋近0.5的矩阵。

均匀性证明：在行变换时，由于所有的行都是随机选择的，这样后面的行变换不会改变前面行中‘1’元素的分布，因而保证了整个矩阵‘1’元素的均匀性。

由于整个矩阵‘1’元素的均匀性，那么任2列，或N列向量相加所得的结果向量中‘1’元素也是均匀的。这种均匀性保证了误码向量均匀扩散的性质，而且矩阵规格N越大，其均匀性越好。

4 性能分析与验证

为了验证用上述变换生成的矩阵中元素‘1’的密度及均匀性，设计了2个实验。第1个实验验证不同规格矩阵中，每列‘1’密度的分布情况；第2个实验验证不同规格矩阵在不同实验次数下‘1’密度的变化。

实验过程中，为了保证所选行是均匀随机的，选用第2代移动通信中的流密码发生器A5/2作为行号选择器，以往大量实验证明A5/2非线性移位寄存器具有较好的伪随机性，因而符合行号随机选取的要求。

为了选取规格N矩阵的行号，每次生成logN个比特，如果这logN个比特所指示的行已经挑选，则放弃重新选择。由于每次生成的logN个比特都是随机的，因而可以保证所选行号的随机性。

实验结果如表1和表2所示。表1中的行表示矩阵规格，列表示密度范围，表中统计数据为矩阵列密度的比例。

表2的行表示矩阵规格，列表示重复实验次数，表中的统计数据为矩阵中元素‘1’的密度。

表1 各列密度统计 (%)

表2 矩阵总体密度

次数12825651210241000.4952830.4971450.4989940.4995133000.4976250.4982350.4990760.499302

从表1可知，随着矩阵规格的增加，各列‘1’的密度也更加趋近0.5，矩阵规格越大均匀性越好。规格为128时，有9.38%的列密度小于0.425，或者大于0.575，而当规格为1 024时，这一数据严格地变为0；从表2可知，随着矩阵规格和重复实验次数的增加，矩阵中‘1’的密度均匀趋向0.5。然而，在实验中并没有发生密度超过0.5的现象，这也许是由于各行线性相关造成的。

从以上实验数据可知，随着矩阵规格、实验次数的增加，矩阵的总体密度、各列的密度都趋向于0.5，这很好地符合了预期。

为了更形象地比较不同密度和不同方法对安全间隙的影响，设计了2个实验。一般可逆矩阵、密度0.2和密度0.45这3种扩散矩阵在不同信噪比下对安全间隙的影响如图4所示。IEEE 802.11标准的LDPC码、删余LDPC码和密度0.45的扩散矩阵对安全间隙的影响如图5所示。

图4 不同密度扩散矩阵

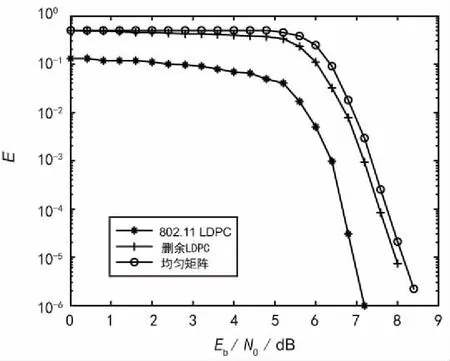
图5 不同方法的扩散矩阵

从图4可知，随着扩散矩阵密度的增加，在相同信噪比下，高密度扩散矩阵的误码率更快地趋近0.5，从而其安全间隙也迅速变小。从图5可知，本文的扩散矩阵相比删余LDPC码有着更好的性能，可以使安全间隙进一步减小。

通过实验分析可知，本文提出的方法可以有效地减小安全间隙，而且构造简便，有着很好的实用价值。

5 结束语

本文沿用1975年Wyner的窃听信道模型，以级联码为基础开展安全编码的研究，提出了一种简便有效地构造均匀扩散矩阵的新方法,解决了构造任意规格、任意密度且均匀、可逆矩阵的问题。实验数据显示，本文方法可以快速构造任意规格、密度均匀、可逆的扩散矩阵，与同类方法相比可以明显缩小安全间隙。

本文是在一般情况下研究均匀扩散矩阵，下一步将考虑在特定环境下应用扩散矩阵有效缩小安全间隙。

[1] WYNER A D.The Wire-tap Channel[J].The Bell System Technical Journal,1975,54(8)：1355-1387.

[2] OZAROW L H,WYNER A D.Wire-tap Channel II[J] The Bell System Technical Journal,1984,63(10)：2135-2137.

[3] HARRISON W K,ALMEIDA J,MCLAUGHLIN S,et al.Coding for Cryptographic Security Enhancement Using Stopping Sets[J].IEEE Transaction on Information Forensics Security,2011,6(3)：575-584.

[4] KLINC D,HA J,MCLAUGHLIN S,et al.LDPC Codes for the Gaussian Wiretap Channel[C]∥IEEE Information Theory Workshop (ITW 2009),Italy：2009：95-99.

[5] KLINC D,HA J,MCLAUGHLIN S,et al.LDPC Codes for the Gaussian Wiretap Channel[J].IEEE Transactions on Information Forensics and Security,2011,6(3)：532-540.

[6] BALDI M,BIANCHI M,CHIARALUCE F.Non-systematic Codes for Physical Layer Security[C]∥IEEE Information Theory Workshop (ITW 2010),2010：1-5.

[7] 王新梅，肖国镇.纠错码—原理与方法[M].西安：西安电子科技大学出版社，2001.

[8] THANGARAJ A,DIHIDAR S,CALDERBANK A R.Applications of LDPC Codes to the Wire-Tap Channel[J].IEEE Transactions on Information theory,2007,53(8)：2933-2945.

[9] KLINC D,HA J,MCLAUGHLIN S,et al.LDPC Codes For Physical Layer Security[C]∥IEEE Global Telecommunications Conf.(GLOBECOM 2009),2009：1-6.

[10] WONG C.W,WONG T.F,SHEA J.M.LDPC Code Design for the BPSK-constrained Gaussian Wiretap Channel[C]∥IEEE Globecom Workshops on Physical-Layer Security,2011：898-902.

[11] BALDI M,BIANCHI M,CHIARALUCE F.Coding with Scrambling,Concatenation,and HARQ for the AWGN Wire-Tap Channel：Asecurity Gap Analysis[J].IEEE Transaction on Information Forensics Security,2012,7(3)：883-894.

[12] TANG X,LIU R,SPASOJEVIC P,et al.On the Throughput of Secure Hybrid-ARQ Protocols for Gaussian Block-Fading Channels[J].IEEE Transactions on Information Theory,2009,55(4)：1575-1591.

[13] HARRISON W.K,ALMEIDA J,KLINC D,et al.Stopping Sets For Physical-Layer Security[C]∥IEEE Information Theory Workshop (ITW 2010),2010：1-5.

[14] KWARK B J,SONG N K,PARK B.Physical Layer Security with Yarg Code[C]∥Proceedings of IEEE International Conference on Emerging Network Intelligence,2009：43-48.

[15] BALDI M,BIANCHI M,CHIARALUCE F.Increasing Physical Layer Security Through Scrambled Codes and ARQ[C]∥IEEE International Conference on Communications Workshops (ICC),2011：1-5.

[16] 熊全淹.近世代数[M].武汉：武汉大学出版社,2004.

ThePhysicalLayerSecurityCodeBasedonOptimalUniformDiffusionMatrix

YANG Yong1,2

(1.CETCKeyLaboratoryofSpaceInformationApplicationTechnology,ShijiazhuangHebei050081,China; 2.The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China)

TN918

A

1003-3106(2017)11-0036-05

杨勇男，(1980—)，博士，高级工程师。主要研究方向：信道编译码、移动通信解密和编码盲识别等。

10.3969/j.issn.1003-3106.2017.11.08

杨勇.基于最佳均匀扩散矩阵的物理层安全编码[J].无线电工程,2017,47(11):36-40.[YANG Yong.The Physical Layer Security Code Based on Optimal Uniform Diffusion Matrix[J].Radio Engineering,2017,47(11)：36-40.]

2017-06-20

国家高技术研究发展计划(“863”计划)基金资助项目(2015AA01A707)；中国电子科技集团公司航天信息应用技术重点实验室基金资助项目(EX156290058)。