面向区域覆盖的遥感卫星轨道布设优化算法

何川东，王 鹏，刘晓东，崔 莉

(北京遥感信息研究所，北京 100192)

面向区域覆盖的遥感卫星轨道布设优化算法

何川东，王 鹏，刘晓东，崔 莉

(北京遥感信息研究所，北京 100192)

面向区域覆盖的遥感卫星轨道布设是典型的多目标优化问题，设计具有针对性的求解模型和高效的求解算法是解决该问题的关键。通过分析体现区域覆盖的主要评价指标，明确问题的基本输入输出和先决条件，建立了该问题的多目标优化数学模型。根据模型特点，基于快速非支配排序遗传算法NSGA-II设计了优化算法，采用快速非支配排序、精英保持、拥挤度距离等策略，减少了计算复杂性，提高了搜索速度。仿真结果表明，基于NSGA-II的卫星轨道布设优化算法可以有效解决面向区域覆盖的卫星轨道布设问题。

区域覆盖；遥感卫星；轨道布设；优化算法

AbstractIt is a typical multi-objective optimization problem to design the orbit of remote sensing satellites for the regional coverage.It is the key to solve this problem by designing a targeted model and an efficient algorithm.By analyzing the main evaluation indicator,the basic input-output and prerequisites of the problem is clarified,and the multi-objective optimization model of the problem is established.According to the characteristics of the model,the optimization algorithm is designed based on NSGA-II,which reduces the computational complexity and improves the searching speed.Simulation results show that the optimization algorithm for satellite orbit design based on NSGA-II can effectively solve the problem of satellite orbit design for regional coverage.

Keywordsregional coverage;remote sensing satellites;satellite orbit design;optimization algorithm

0 引言

针对特定区域的覆盖成像是遥感卫星成像任务中一类重要的成像任务，如针对重大自然灾害监测(如地震区域覆盖、森林火灾覆盖、河流/近海浮冰监测等)的区域覆盖、国土资源普查和海洋环境监视等，这些任务都是针对特定区域、在特定时间范围内、具有特定成像要求的成像任务。区域覆盖任务一般都具有较高的时效性要求，如针对重大自然灾害的遥感图像保障，一般具有持续时间短、范围有限的特点，这就要求遥感卫星能在较短的时间内，对特定区域进行无缝覆盖。现代遥感卫星都具有轨道机动能力，通过轨道机动，将多颗卫星星下点轨迹合理布设，可以实现对特定区域的无缝覆盖。

近年来，随着智能优化算法的发展，采用遗传、模拟退火和神经网络等现代智能优化算法进行卫星轨道设计，可以在更广泛的解空间进行搜索，使搜索速度加快，同时搜索出的方案也更优。文献[1]针对全球连续覆盖卫星轨道的优化设计，采用多目标遗传算法，并与 STK集成，实现了星座覆盖特性的评价。文献[2]以提高星座覆盖特性与减小卫星数量为优化目标，提出了基于启发式的遗传算法进行区域覆盖星座的设计。文献[3]针对最大覆盖间隙和平均覆盖间隙2个优化目标，利用遗传算法解决了稀疏星座设计问题。国内在卫星轨道布设及星座设计方法上也进行了广泛研究。文献[4]研究了针对全球和区域覆盖星座的覆盖原理和设计方法。文献[5]基于遗传算法对区域覆盖卫星星座优化设计进行了研究。文献[6]提出了一种能同时兼顾星座结构和参数的进化算法解决区域覆盖卫星星座的设计问题。

本文针对区域覆盖的特点，设计了考虑最大化覆盖次数、覆盖率与最小化卫星数量3个优化目标的数学优化模型，提出了基于NSGA-II的卫星轨道布设优化算法，在有限的时间内解决了面向区域覆盖的遥感卫星轨道布设问题，满足了工程应用的要求。

1 模型建立

数学模型是求解面向区域覆盖的遥感卫星轨道布设问题的基础，只有将问题准确的描述和界定，才能解决所提出的问题。该问题可以描述为：给定一区域和若干遥感卫星，在一定轨道布设策略指导下，得到目标区域覆盖率最大、最大重访时间间隔最小、卫星数量最少的卫星轨道布设方案，从而实现在特定时间段内对特定区域的无缝覆盖。

1.1 评价指标

不同的遥感卫星成像系统对某一个特定区域的成像能力不一样，为了方便对不同遥感卫星轨道布设方案进行评价，必须定量化评价遥感卫星对特定区域的成像能力，这种定量尺度就称为卫星成像能力评价指标。为了充分比较不同遥感卫星轨道布设方案的优劣、体现特定区域目标的成像要求，建立合适的卫星成像能力指标并能够量化计算是该问题求解的关键[7]。从区域覆盖角度揭示遥感卫星对特定区域成像能力的能力指标主要有：覆盖次数、覆盖率和覆盖面积等[8]。

1.1.1 有效覆盖面积Se

在特定时间段内，遥感卫星对特定区域的无重复覆盖面积之和，即有效面积。计算有效覆盖面积不仅需要去除单颗卫星不同条带之间的重复面积，还需要去除不同卫星同一目标点之间的重复面积。设卫星e的有效覆盖面积为：

(1)

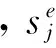
1.1.2 覆盖次数Cnumber(j)

遥感卫星对特定区域内目标点覆盖一次，称为一次覆盖。所有卫星对目标点只有一次覆盖即为单重覆盖，单颗卫星多次或多颗卫星覆盖同一目标点即为多重覆盖。对于目标区域中第j个目标点的覆盖次数Cj即为各颗卫星覆盖第j个目标点的时间窗口数目的总和：

(2)

式中，TNej为第e(e=1,2,…k)颗卫星对目标点j的可见时间窗口的个数。

1.1.3 覆盖率Crate

在特定时间段内，遥感卫星对特定区域的有效覆盖面积之和与特定区域的面积比值即为覆盖率。设特定区域的总面积为S，则覆盖率定义为：

(3)

1.2 数学模型

遥感卫星对特定区域覆盖的轨道布设问题首先需满足以下约束条件：

① 最大重访时间间隔满足用户需求；

② 覆盖率满足用户需求；

③ 地面分辨率满足用户需求；

④ 传感器类型满足用户需求。

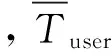
根据区域覆盖的主要评价指标，该问题求解的优化目标需满足：最大化覆盖次数、最大化覆盖率和最小化卫星数量。这样，面向区域覆盖的遥感卫星轨道布设目标函数为：

Max(Cnumber)，

(4)

Max(Crate)，

(5)

Min(S)。

(6)

s.t.

(7)

Crate≥Cuser，

(8)

VRmin≥VRuser，

(9)

VS≥VSuser。

(10)

2 算法研究

多目标优化问题由于其多个优化目标之间常常存在冲突，很难找到一个解在各个优化目标上都优于其他解，传统完全搜索算法难以满足求解要求，现代智能搜索算法(随机搜索算法)便应运而生，遗传算法(GA)[9]即是现代智能搜索算法的一种。遗传算法具有内在并行性，可以对整个解空间进行并行搜索，常用来求解传统搜索算法难以解决的复杂的、非线性的问题。本文基于快速非支配排序遗传算法设计了问题求解算法。

2.1 快速非支配排序遗传算法NSGA-II

多目标遗传算法的核心就是协调各目标函数之间的关系，找出使各目标函数能尽量达到比较大(或比较小)的最优解集[10]。经典遗传算法主要采用简单的选择、交叉和变异等操作步骤，对复杂应用场合的求解效果并不理想，后来通过不同的遗传基因表达方式，不同的交叉、变异算子的设计，以及一些特殊算子的引用等方式，产生了以经典遗传算法为核心的各种优化算法。

快速非支配排序遗传算法NSGA-II (Non-dominated Sorting Genetic Algorithm)[11]就是一种基于经典遗传算法产生的智能搜索算法。快速非支配排序遗传算法通过采用快速非支配排序策略、精英策略和拥挤距离策略而得到的一种多目标进化算法，其最显著优点就是采用了快速非支配排序和排挤机制，从而减少了计算复杂性，提高了算法搜索速度。

2.2 基于NSGA-II的卫星轨道布设算法流程

2.2.1 染色体设计

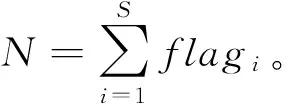
图1 轨道布设方案编码表示方法

2.2.2 种群初始化

种群初始化主要有2种方式：启发式方法和随机方法。2种方式各有优缺点，启发式方法可以提高算法搜索速度，但可能导致局部最优；随机方法可以保证种群的多样性，但可能降低搜索速度。本文种群初始化时采用2种方式的结合：一方面种群初始化时考虑到卫星星下点轨迹的平均分布，这些解的优化性较好，能加快搜索速度；另一方面，种群初始化时采用随机方法，这些解的个体分布性较好，能扩大候选解空间。

2.2.3 快速非支配排序

快速非支配遗传算法在进行选择、交叉和变异等经典遗传算法操作步骤前，首先根据个体的支配关系对候选种群进行分层。该步骤需要计算种群P中每个个体i的2个参数ni和Si，其中ni为种群中支配个体i的个体数，Si为种群中被个体i支配的个体集合。快速非支配排序后每个个体都得到一个属性值，即非支配层数irank，快速非支配排序的流程如图2所示。

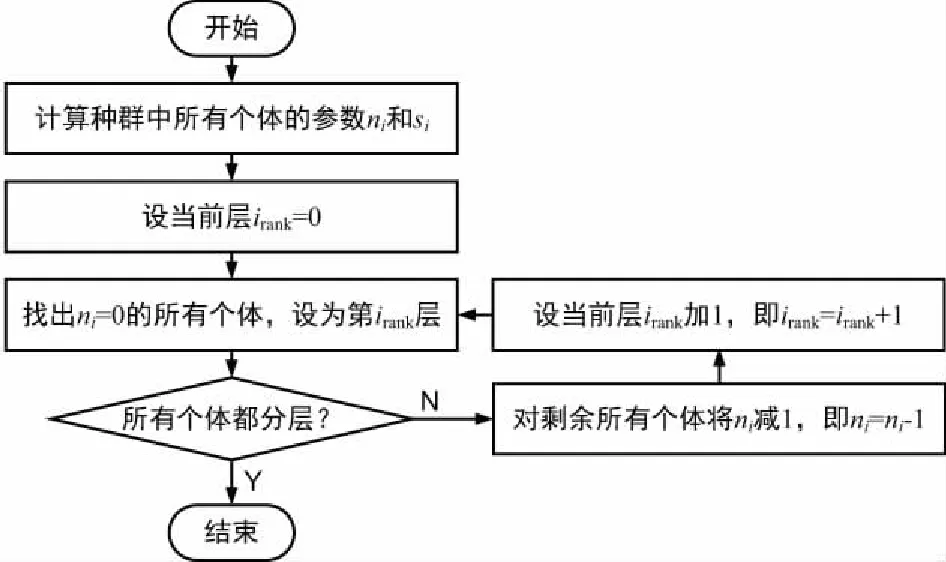
图2 快速非支配排序流程

2.2.4 拥挤距离计算

拥挤度距离的概念即：种群中给定候选解i的周围个体密度，设为L[i]d。拥挤度距离越大说明周围其他个体距离个体i越远，种群分布较分散，有利于扩大解空间找到全局最优解；拥挤度距离越小说明周围其他个体距离个体i越近，种群分布较集中，不利于扩大解空间搜索范围，容易陷入局部最优。拥挤度距离计算流程如图3所示。

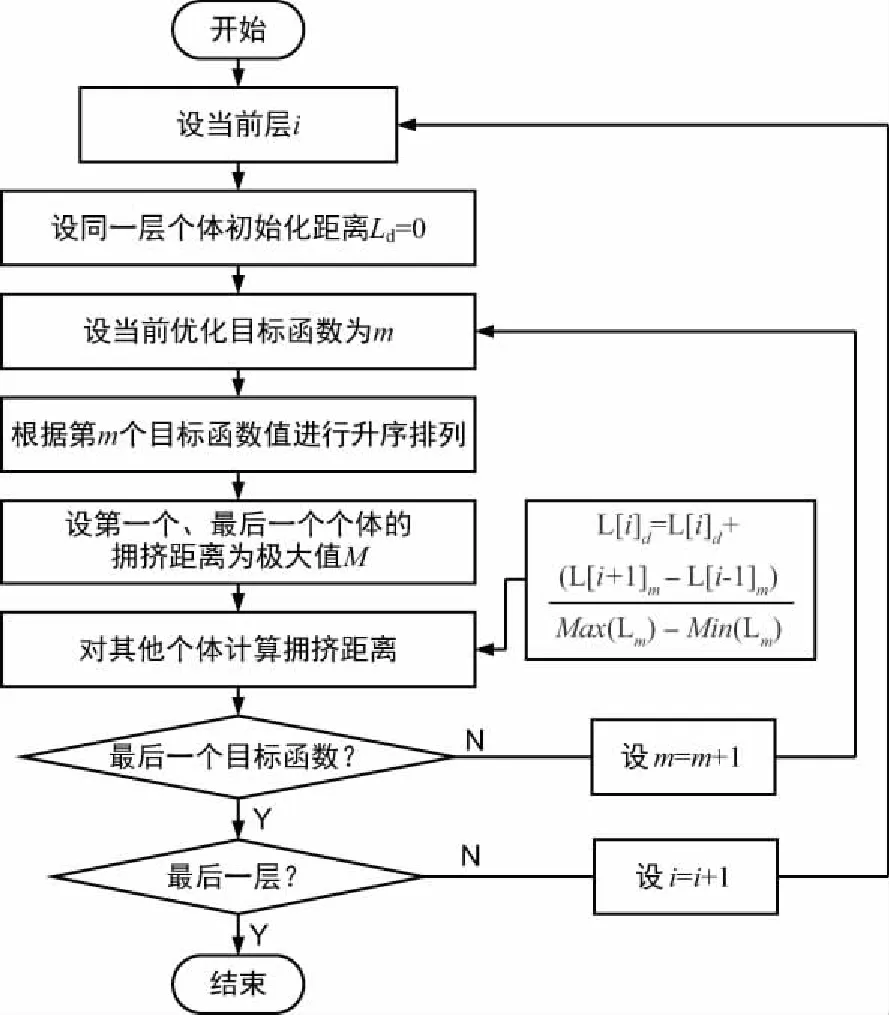
图3 拥挤度距离计算流程

2.2.5 拥挤度选择

经过上述非支配排序和拥挤距离计算2个步骤，种群中的每个个体i都得到2个属性值：非支配层数irank和拥挤距离id。随机选择2个个体进行比较，选择规则定义为：

当irankjd时，选择个体i。

即优先选择非支配层数低的；如果非支配层数一样，则选择拥挤度距离大的。

2.2.6 精英保持

精英保持策略是遗传算法确保收敛的必要条件，是提高全局收敛性和搜索速度的重要方法。精英保持策略即将父代种群与其产生的子代种群进行合并，共同竞争产生子种群，为了防止优良个体由于交叉、变异操作而破坏，对适应度高的个体不进行交叉和变异，直接复制进入下一代子种群，这样有利于保持父代种群中的优良个体进入下一代，迅速提高种群水平。精英保持的流程如图4所示。

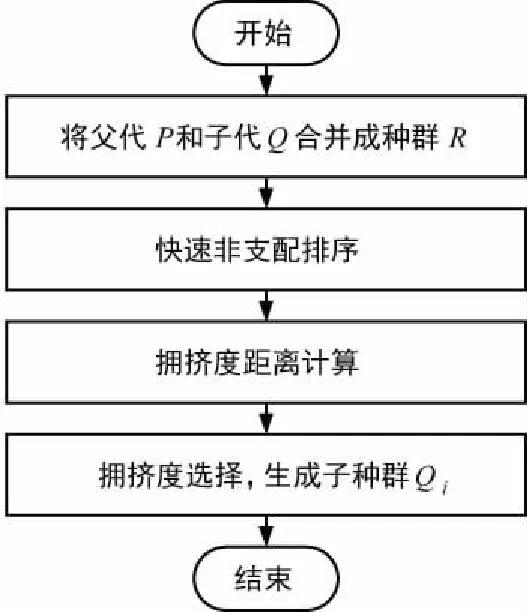
图4 精英保持流程

2.2.7 算法流程

基于NSGA-II的面向区域覆盖的遥感卫星轨道布设优化算法的基本流程如图5所示。

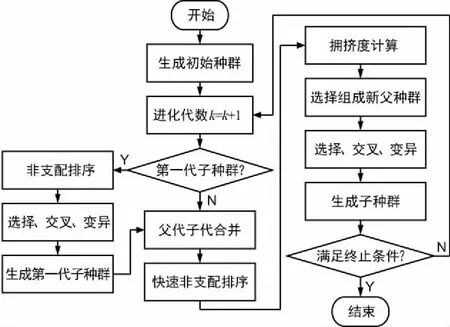
图5 算法流程

3 仿真实验

本文对算法进行了仿真实验以验证算法的有效性，采用Windows XP操作系统，编程工具为VisualStudio2010。仿真中，设针对西南某地重大自然灾害监测任务，该目标的区域范围为：左上角顶点经纬度为(106.68°，24.27°)，右下角顶点经纬度为(108.68°,22.4°)。设该任务的成像要求为最大重访间隔时间小于10 h，面积覆盖率大于80%，最小分辨率为3 m，传感器类型为光学、雷达与电子3类。仿真周期设为7 d，2016年7月22日～2016年7月29日。假设总共有15颗遥感卫星可以用于对该任务实施成像，轨道根数设为太阳同步轨道数据[12]。

上述区域任务的目标区域范围、成像要求以及仿真周期可以根据具体应用要求进行设置，只是数值变化而已，并不影响本文建立的求解模型、算法对问题求解的适用性。算法运行后，卫星星下点轨迹布设情况如图6所示，针对该任务的轨道布设前后主要评估指标如表1所示。

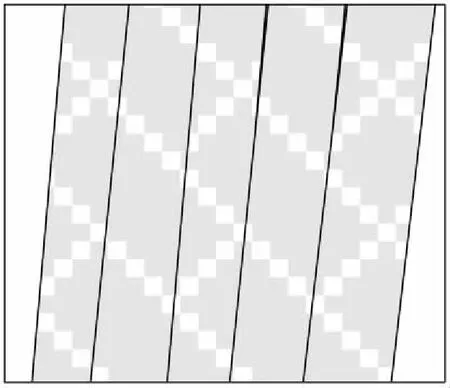
图6 卫星星下点轨迹分布示意

表1 调配方案指标评估值

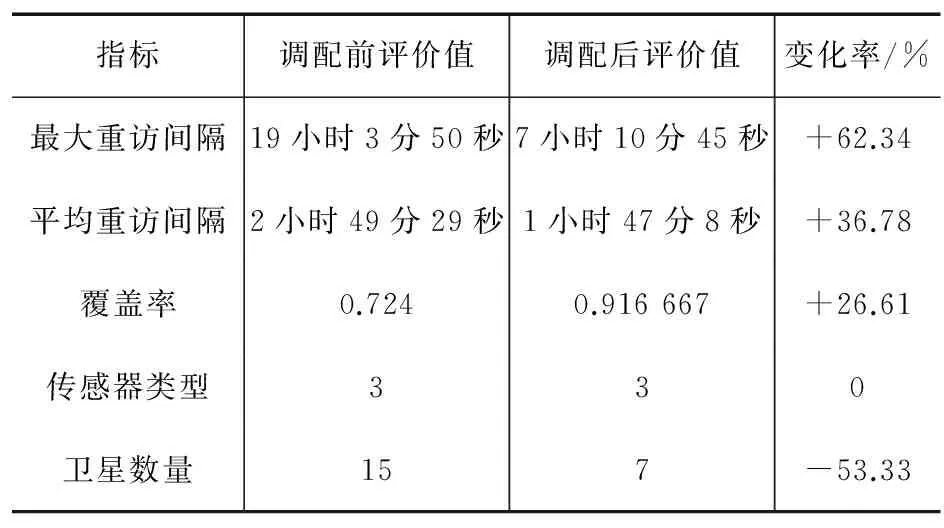
指标调配前评价值调配后评价值变化率/%最大重访间隔19小时3分50秒7小时10分45秒+62.34平均重访间隔2小时49分29秒1小时47分8秒+36.78覆盖率0.7240.916667+26.61传感器类型330卫星数量157-53.33

从仿真结果可以看出，针对特定区域任务，采用面向区域覆盖策略的轨道布设模型，利用基于快速非支配排序遗传算法的优化算法，在较短的时间内获得了满足特定任务要求的卫星轨道布设方案。

4 结束语

本文针对面向区域覆盖的遥感卫星轨道布设问题，从区域覆盖方面建立了卫星成像能力评估指标，并通过分析问题求解的约束条件与优化目标，建立了数学模型。基于快速非支配排序遗传算法，建立了面向区域覆盖的遥感卫星轨道布设求解算法。仿真实验表明，基于快速非支配排序遗传算法设计的卫星轨道布设优化算法，能考虑区域覆盖的覆盖次数、覆盖率和卫星数量等多目标特性，能在有限时间内快速找到符合任务要求的优化布设方案。

[1] MASON W J,COVERSTONE-CARROLL V,HARTMANN J W.OptimalEarth orbiting satellite constellations via a Pareto Genetic Algorithm[C]∥AIAA/AAS Astrodynamics Specialist Conference and Exhibit,Boston,MA,1998:169-177.

[2] ELY T A,CROSSLEY W A,WILLIAMS E A.Satellite Constellation Design for Zonalcoverage Using Genetic Algorithms[C]∥Proceedings of the AAS/AIAA Space Flight Mechanics Meeting,Monterey,CA,1998:443-460.

[3] WILLIAMS E A,CROSSLEY W A,LANG Th J.Average and Maximum Revisit Timetrade Studies for Satellite Constellations Using a Multiobjective Geneticalgorithm[J].Journal of Astronautical Sciences,2001,49：385-400.

[4] 白鹤峰.卫星星座的分析设计与控制方法研究[D].长沙:国防科学技术大学,1999.

[5] 王瑞,马兴瑞,李明.采用遗传算法进行区域覆盖卫星星座优化设计[J].宇航学报,2002,5(3)：24-28.

[6] 陈琪锋,戴金海,张玉琨.区域覆盖星座结构与参数同时优化的进化算法[J].系统工程与电子技术,2004,6(3)：550-553.

[7] 李长春.成像观测小卫星应急组网方法研究[D].长沙:国防科学技术大学,2010.

[8] 魏蛟龙,岑朝辉.基于蚁群算法的区域覆盖卫星星座优化设计[J].通信学报,2006,27(8):68-72.

[9] 王小平,曹立明.遗传算法[M].西安:西安交通大学出版社,2002.

[10] 雷德明,严新平.多目标智能优化算法及其应用[M].北京:科学出版社,1985.

[11] 高媛.非支配排序遗传算法(NSGA)的研究与应用[D].杭州:浙江大学硕,2006.

[12] 范丽,张育林.区域覆盖混合星座设计[J].航天控制,2007,25(6):52-55.

OptimizationAlgorithmofRemoteSensingSatellitesOrbitDesignforRegionalCoverage

HE Chuan-dong,WANG Peng,LIU Xiao-dong,CUI Li

(BeijingInstituteofRemoteSensingInformation,Beijing100192,China)

TP391

A

1003-3106(2017)11-0031-05

何川东男，(1982—)，硕士，工程师。主要研究方向：卫星任务管理控制技术、遥感与地理信息集成技术。

10.3969/j.issn.1003-3106.2017.11.07

何川东,王鹏,刘晓东,等.面向区域覆盖的遥感卫星轨道布设优化算法[J].无线电工程,2017,47(11):31-35.[HE Chuandong,WANG Peng,LIU Xiaodong,et al.Optimization Algorithm of Remote Sensing Satellites Orbit Design for Regional Coverage[J].Radio Engineering,2017,47(11):31-35.]

2016-12-09

王鹏男，(1977—)，硕士，高级工程师。主要研究方向：卫星任务管理控制技术、规划调度优化算法。