低轨卫星导航系统多场景多普勒定位解算方法

邓志鑫，高 宏，王立兵

(1.卫星导航系统与装备技术国家重点实验室，河北 石家庄 050081； 2.中国人民解放军63961部队，北京 100012)

低轨卫星导航系统多场景多普勒定位解算方法

邓志鑫1，高 宏2，王立兵2

(1.卫星导航系统与装备技术国家重点实验室，河北 石家庄 050081； 2.中国人民解放军63961部队，北京 100012)

低轨卫星及快速响应卫星非常适合作为导航源为地面用户提供独立于GNSS的导航定位服务，为了解决用户在不同低轨卫星可见数量条件下的连续定位解算问题，并避免传统伪距定位体制所需要解决的高精度星间时间同步问题，提出多种不同可见星数量条件下仅利用卫星多普勒观测信息的定位解算方法。仿真结果表明，该方法在大部分区域内都能够满足优于20 m的三维定位误差。

低轨卫星；多普勒定位；网格搜索；最小二乘

AbstractFast response and low orbit satellites are very suitable for positioning service as navigation sources independent of GNSS for ground users.In order to solve the problem of continuous positioning solution under the condition of different number of low orbit satellites visible to users,and to avoid the increase of system complexity due to high precision synchronization required by traditional pseudo-range positioning system,a positioning method is proposed only using the Doppler satellite observation information under the condition of different visible satellite number.Simulation analysis results show that this method can meet the requirement for three-dimensional positioning error of less than 20 m in most areas.

KeywordsLEO satellite;Doppler locating;grid search;least square

0 引言

在复杂的电磁干扰环境下,GNSS导航系统中大量的低成本、未加特殊抗干扰措施的导航终端将无法工作[1]。在南北两极地区，由于GNSS系统星座采用低倾角设计方案[2]，导致覆盖性大幅降低。因此，构建GNSS备份无线电导航系统是近年来的研究热点[3-4]。

低轨卫星具有覆盖区域广、可全天候工作以及可观测性较好等特点[5]，微纳卫星、快速响应卫星还具备建设周期短、成本低廉等优势[6]，因此，低轨卫星及快响卫星等微小卫星平台非常适合作为导航源为地面用户提供独立于GNSS的导航定位服务。

GNSS导航系统用户通过观测至少4颗GNSS卫星信号的伪距信息进行定位解算[7]。但是该方法应用于低轨卫星导航系统存在2个问题：① 由于受到低轨卫星数量限制，大部分区域内的地面用户无法同时观测到4颗及以上的低轨卫星[8]；② 采用伪距定位解算的前提条件是多颗卫星必须要实现严格的时间同步[9]，这将极大地增加系统的建设复杂度。而低轨卫星由于运动速度很快，具有较好的多普勒观测性[10]，因此利用多普勒观测信息进行定位解算是低轨卫星导航系统的首选。

近日，美国铱星通信公司宣布其研制的卫星授时与定位(STL)系统已经具备作为GPS备份或是GPS补充的能力。该系统通过66颗低轨卫星及多普勒定位体制为用户提供比GPS更不易受攻击的导航服务，但是并未给出具体的定位解算方法。2011年1月，Mark S.Asher等人在国际会议中[11]提出采用单颗LEO卫星为地面静止用户提供定位手段的思路，但是未给出具体的计算过程，并且其算法需要用户机发射信号给低轨卫星，这不利于用户位置的隐蔽。2013年西南交通大学潘磊[12]分析了多普勒定位的原理，并得出了多普勒定位精度与多普勒测量精度、站址位置精度和速度精度有关的结论，但是并未给出适应多种不同可见星数量条件下的多普勒定位解算方法。

综上所述，如何利用少量的多普勒观测信息实现多种不同可见星数量条件下的连续定位解算是低轨卫星备份导航系统必须解决的关键问题。本文提出了一种仅利用卫星多普勒观测信息的精确定位解算方法，给出了计算流程并分析了该方法的仿真试验性能。

1 多场景条件下的多普勒定位解算方法

1.1 牛顿最小二乘迭代定位解算

由低轨卫星备份导航系统的覆盖性分析可知，地面用户的可见星数量由遮蔽角、轨道倾角、轨道高度和每个轨道的卫星数量等因素决定，一般情况下，特定地点的可见卫星数量为1～4颗不等，因此必须采取能够适应不同可见星数量的定位解算方法，以满足不同场景下的连续导航定位需求。

本文提出能够应用于多场景下的多普勒定位解算方法，该方法能够最大程度地满足不同可见星数量条件的连续定位解算需求。每个历元时刻的定位解算结果由牛顿最小二乘迭代过程获得，其迭代计算公式为：

[xi+1,yi+1,zi+1]T=[xi,yi,zi]T+[Δxi+1,Δyi+1,Δzi+1]T，

(1)

式中，[xi,yi,zi]T为第i次(i为自然数)迭代后的定位解算结果；[Δxi+1,Δyi+1,Δzi+1]T为第i+1次迭代的定位结果修正量，并有

[Δxi+1,Δyi+1,Δzi+1]T=(GT×G)-1×GT×Y，

(2)

式中，

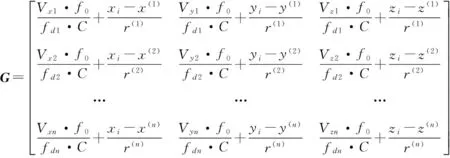
(3)

Y=

(4)

[x(j),y(j),z(j)]T(j=1，2，…n,n≥3)为第j颗低轨卫星或低轨卫星第j个观测点的三维位置坐标；r(j)为第j颗低轨卫星或低轨卫星第j个观测点与用户第i次位置迭代解算结果的观测距离，即

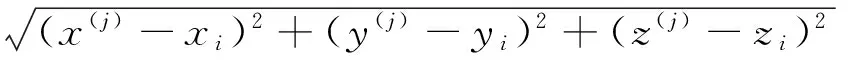
[Vxj,Vyj,Vzj]T为第j颗低轨卫星或低轨卫星第j个观测点当前时刻的三维速度；f0为低轨卫星信号的载波频率；fdj为第j颗低轨卫星或低轨卫星第j个观测点的观测多普勒频率。当Y的2-范数小于某固定常数Dy时，迭代计算结束，得到定位解算结果，否则继续进行迭代计算。

1.2 大区域网格搜索定位解算初值确定

采用牛顿迭代定位解算方法具有计算量小、定位精度高和卫星可见星数量适应性强的特点，但是如果用户位置初值与真实值距离较远，如大于100 km以上时，可能会导致迭代计算结果不收敛的情况。为了解决该问题，可采用大区域网格搜索方法实现用户在百km量级的粗定位，再将粗定位结果作为牛顿迭代定位解算方法的初值，从而实现大区域范围内的高精度稳健定位解算。

网格搜索定位解算初值确定方法为：首先将大区域范围按照经纬度划分为等间距的网格，将每个网格点经纬高坐标转化为ECEF坐标，然后在相同的卫星观测数量或卫星观测点条件下计算牛顿迭代定位解算方法中的残差值：

Y=

(5)

式中，[xk,yk,zk]T为第k个网格点的ECEF坐标，求取Y的2-范数的最小值，其所对应的网格点坐标即可作为牛顿最小二乘多普勒定位解算的迭代初值。

1.3 定位解算工作模式与精度提升

上述多普勒定位解算方法有单历元定位模式和连续观测定位模式2种应用模式。单历元定位模式是指利用单历元多普勒观测信息即可实现用户的实时定位，一般而言，当用户可见星数量≥3时，则可工作于单历元定位模式。连续观测定位模式是指利用多历元多普勒观测信息实现静态用户的联合定位，一般当用户可见星数量<3时，则工作于连续观测定位模式。上述为一般情况下的工作模式划分，有一个特例是如果用户可见星数量为2，又具备用户高程观测信息，则同样可工作于单历元定位模式，即通过2颗低轨卫星的多普勒观测信息和用户高程观测信息实现用户单历元三维定位。此时的定位解算方法与上面介绍的方法相类似，只不过其中G和Y的计算公式变为：

(6)

Y=

(7)

式中，ah=a+h；bh=b+h；a和b分别为地球的长、短半轴长度；h为用户的海拔高度估计值。

如果低轨卫星可见数量为1，则只能采用单星多普勒信息连续观测的方法实现定位解算，单星连续观测的原理如图1所示。由于低轨卫星运行速度快，用户可观测时间约为几分钟，在有限的观测时间内选取3个及以上的多普勒信息观测点即可实现用户的连续观测定位解算，观测点的选取应尽量满足DOP值最优的原则。在此时间内用户本地时钟的漂移所引入的误差较小，可忽略不计。

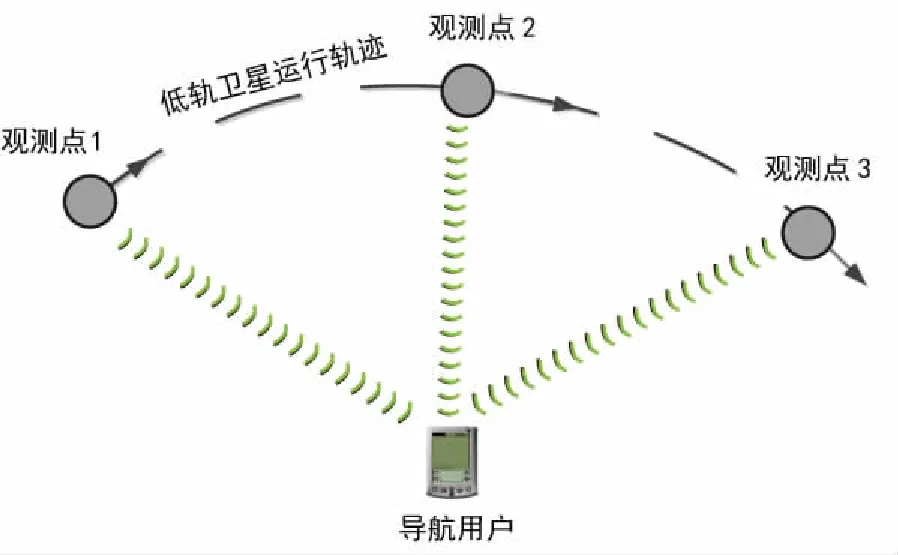
图1 单星连续观测多普勒定位示意

无论是单历元定位模式还是连续观测定位模式，如果用户处于静止状态，则可通过多组去除野值后的定位解算结果平滑方法进一步提升定位解算精度，此时的定位解算结果[x,y,z]T计算公式为：

(8)

式中，定位解算结果[x,y,z]T为ECEF三维定位坐标；N为定位结果平滑点数；[xk,yk,zk]T为第k个定位解算结果。

2 定位解算性能仿真验证

参考美国铱星系统[13]，轨道高度780 km，卫星轨道与赤道面倾角为86.4°，星座由6个轨道面组成，每个轨道面11颗星。其全球卫星布局如图2所示。显然，高纬度地区的卫星可见性较好，赤道地区的卫星可见性最低，因此下面仅仿真分析赤道地区的星座覆盖性能。赤道地区的典型低轨卫星布局单元如图3所示。基本布局单元的可见性分布如图4所示，其中黑色代表可见1颗星、灰色代表可见2颗星、白色代表可见3颗星。

图2 铱星系统低轨卫星全星座布局

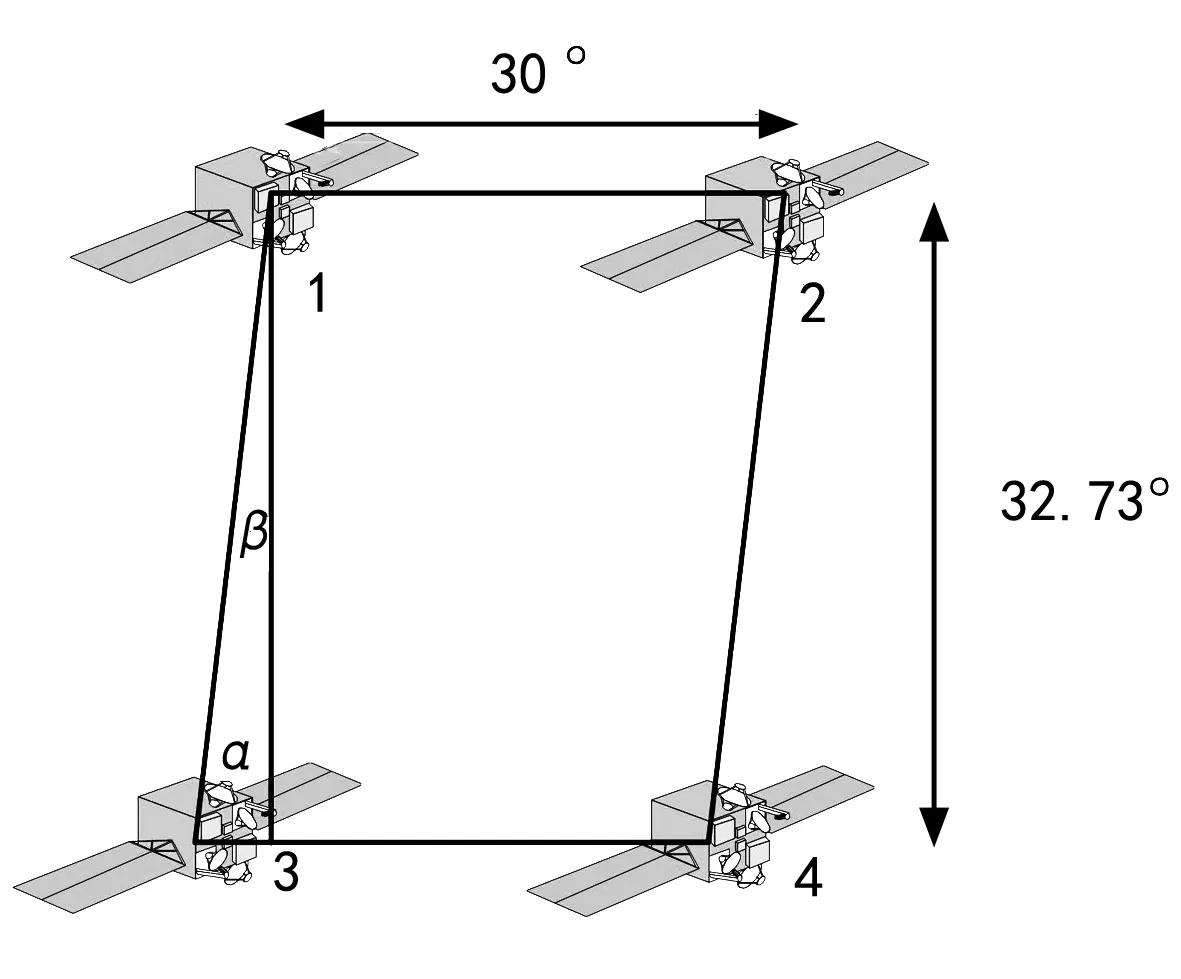
图3 低轨卫星赤道地区典型布局单元

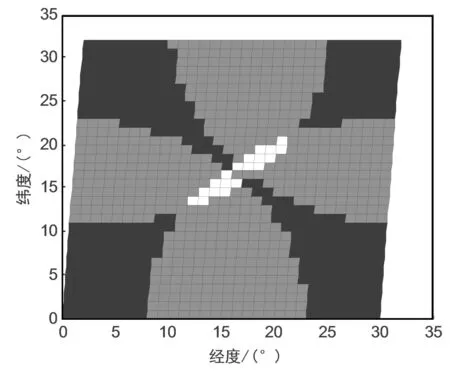
图4 遮蔽角5°时的基本布局单元可见性分布

设伪卫星定轨误差各方向1 m，多普勒测量误差1 Hz，卫星各方向速度播发误差0.1 m/s，用户高程方差5 m，则可见3颗低轨卫星时的多普勒定位误差分布如图5所示。图5中，黑色表示3星定位误差小于20 m的区域，约占可定位区域的95%；灰色表示大于20 m的区域；白色表示非3星定位区域。

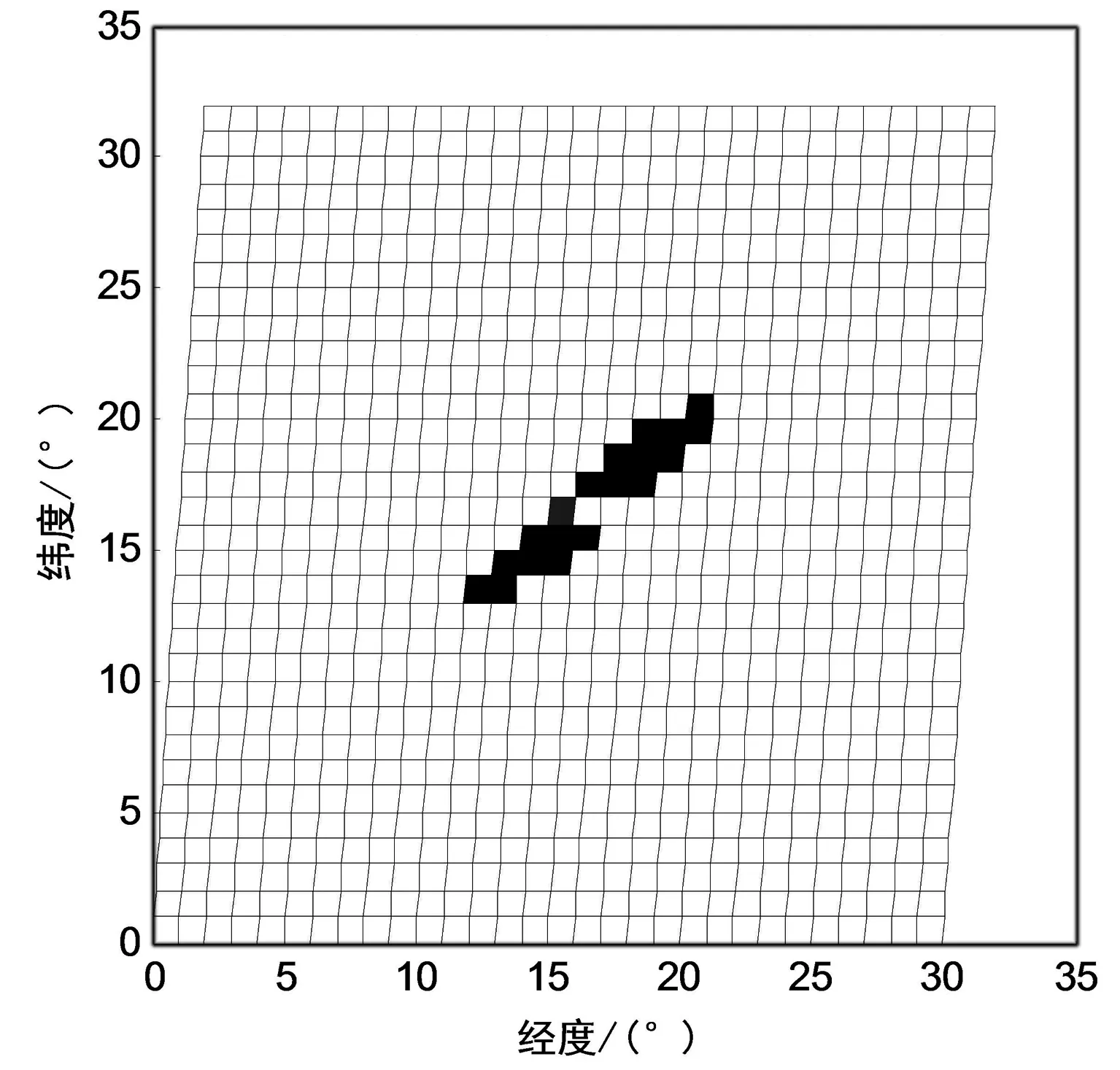
图5 三星多普勒定位误差分布

双星多普勒及高程联合定位误差分布如图6所示，其中灰色表示定位误差小于20 m，约占总定位区域的85%；白色为大于20 m；黑色为非双星定位区域。

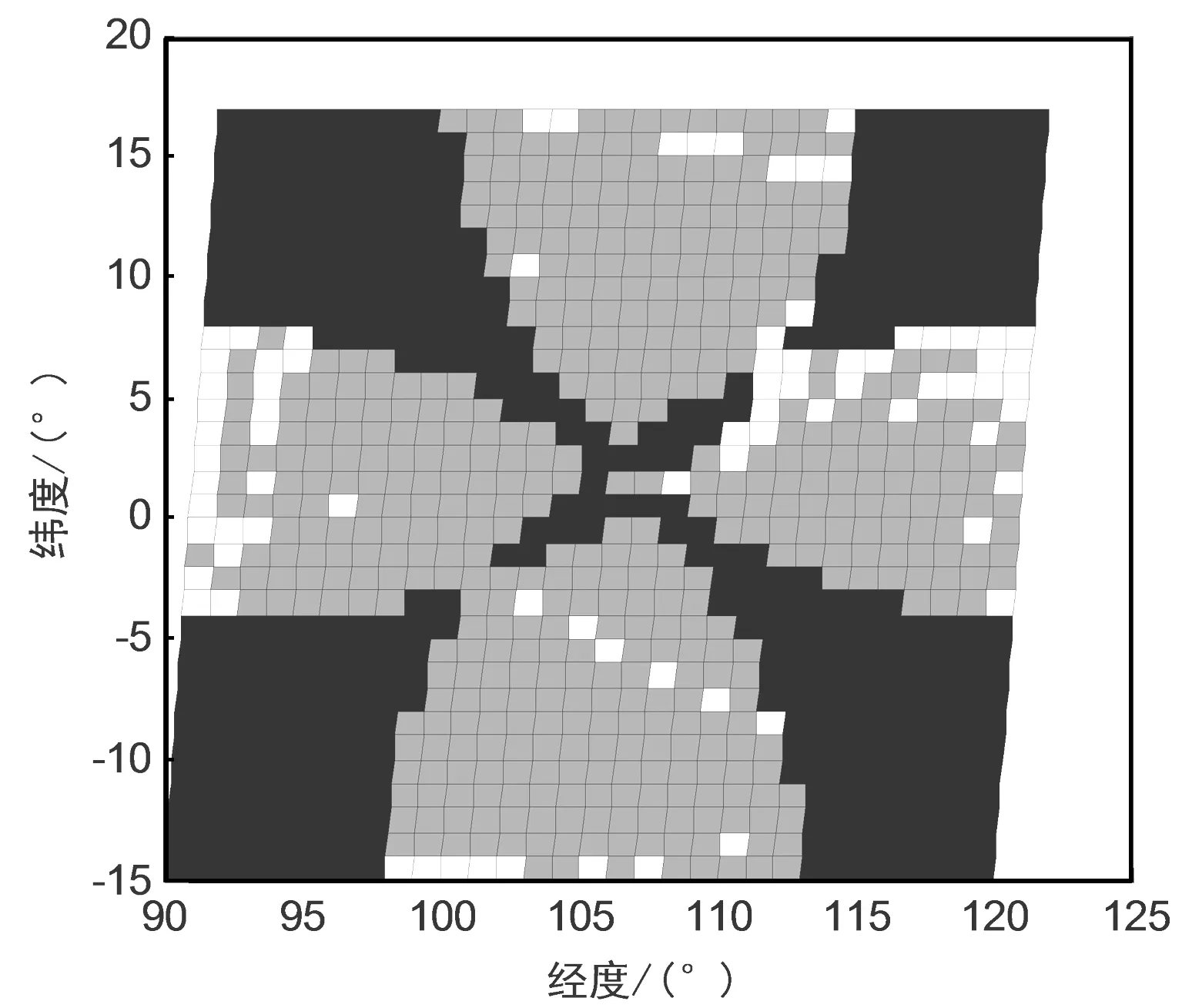
图6 双星多普勒高程单历元联合定位误差分布

单星连续观测5 min的定位误差分布如图7所示。其中灰色表示定位误差小于20 m，约占可定位区域的92%；白色为大于20 m；黑色为非单星定位区域。

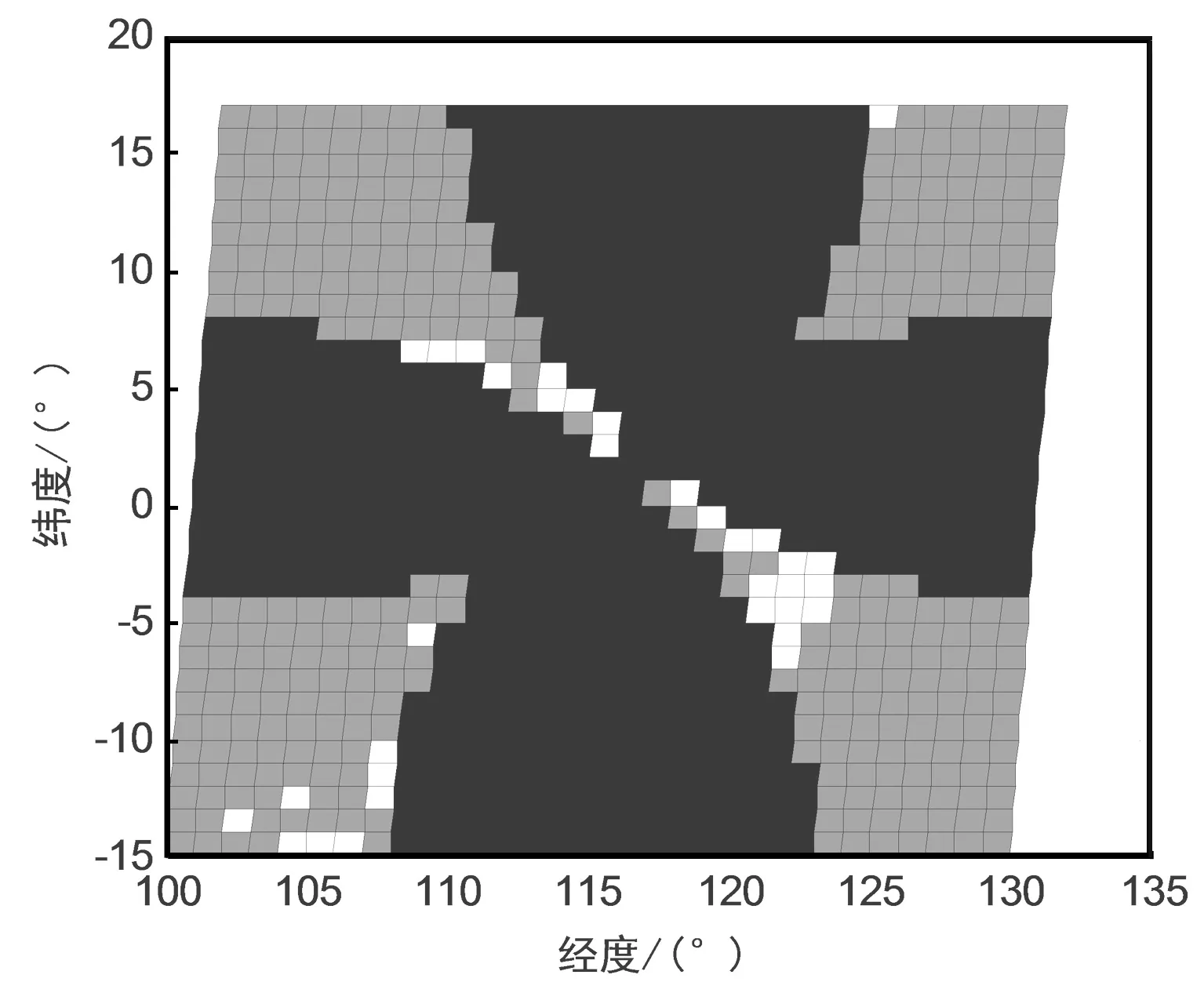
图7 单星连续观测5 min多普勒定位误差分布

采用多普勒观测量进行定位解算时，每个瞬间都会有若干位置因多普勒观测值影响导致定位精度较低，但是随着卫星在轨道中运行，定位精度较差的地点快速发生变化，因此无论哪种多普勒定位解算方法，只要连续观测几个历元，并进行去除野值后的平滑处理即可得到更为精确的定位精度。经过3个历元平滑后的低轨星座典型布局单元多场景联合定位误差分布如图8所示，图8中白色区域表示定位误差小于20 m；黑色区域为定位误差大于20 m，可知，三维定位误差优于20 m的区域提升至98.3%，如果进一步增加平滑历元个数可进一步提升定位精度。

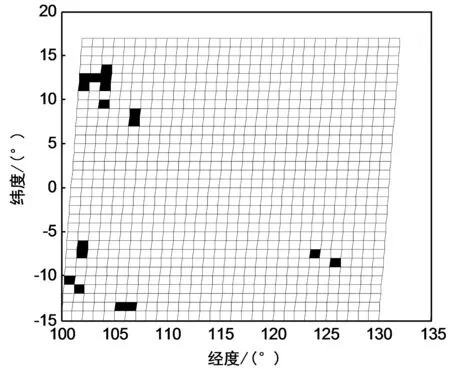
图8 多场景多普勒定位误差小于20 m分布

3 结束语

低轨卫星备份导航系统具有覆盖区域广、可全天候工作的优势，采用多普勒定位体制可规避高精度星间时间同步带来的系统建设复杂度问题[14]，对于多星间的频率同步问题，则有多种方法来实现，例如GNSS卫星导航校频、地面双向校频和星间校频等[15]，载荷易于与通信、遥感卫星相集成，具有较好的应用可行性。

本文提出了一套可适用于任意可见星数量的网格搜索与牛顿最小二乘迭代相结合的多普勒定位解算方法，可解决任意低轨星座场景下的自适应定位解算问题，仿真结果表明在典型场景下能够满足大于98%的覆盖区域内实现优于20 m的三维定位精度，能够满足大部分静态及低动态用户的导航定位应用需求。

[1] 刘荣，王立平，陈杨.GPS接收机抗干扰性能仿真研究[J].无线电通信技术，2014，40(1)：58-60.

[2] 郑炜，李斌，任术波，等.GEO卫星斜投影多波束的椭圆参数分析[J].无线电通信技术，2013，39(1)：5-7.

[3] 王珏，何成龙，张金涛，等.基于模糊区的卫星导航空时测量技术研究[J].无线电工程，2015，45(4)：46-49.

[4] 张云，崔晓伟，笪腾飞，等.基于软件无线电的GNSS干扰和多径监测系统设计[J].电讯技术，2017,57(3)：288-295.

[5] 冯少栋，揭晓，李仰志，等.低轨星座系统业务建模与仿真[J].宇航学报，2010，31(1)：179-184.

[6] 曾德林.快速响应小卫星星座设计及覆盖性能仿真分析[J].计算机仿真，2014，31(6)：73-77.

[7] 刘竞超.复杂环境下GNSS接收机快速定位研究与分析[D].北京：北京邮电大学，2013.

[8] 杨斌，何锋，靳瑾，等.LEO卫星通信系统覆盖时间和切换次数分析[J].电子与信息学报，2014，36(4)：804-809.

[9] 李东新，杨伟才，常青，等.伪卫星共视法时间同步模式及精度分析[J].导航定位与授时，2015，2(4)：40-47.

[10] 商春恒.单星无源定位中多普勒信息参数测量技术研究[D].北京：北京理工大学，2015.

[11] ASHERM S,STAFFORD S J,BAMBERGER R J,et al.Radionavigation Alternatives for US Army Ground Forces in GPS Denied Environments[C]∥International Technical Meeting of the Institute of Navigation,2011：508-532.

[12] 潘磊.基于多普勒频率差的机载无源定位技术研究[D].成都：西南交通大学，2013.

[13] 潘科炎.铱星星座动力学——系统工程综合[J].控制工程，2000(1)：29-38.

[14] 徐义.基于多普勒信息的单星无源定位新技术研究[D].长沙：国防科学技术大学，2009.

[15] 吴苗，朱银兵，李方能，等.无线电导航原理与信号接收技术[M].北京：国防工业出版社，2015.

Mutiple-sceneDopplerLocatingMethodforLEOSatelliteNavigationSystem

DENG Zhi-xin1,GAO Hong2,WANG Li-bing2

(1.StateKeyLaboratoryofSatelliteNavigationSystemandEquipmentTechnology,ShijiazhuangHebei050081,China; 2.Unit63961,PLA,Beijing100012,China)

TN965.5

A

1003-3106(2017)11-0049-05

邓志鑫男，(1982—)，博士，高级工程师。主要研究方向：卫星导航增强技术。

10.3969/j.issn.1003-3106.2017.11.11

邓志鑫,高宏,王立兵.低轨卫星导航系统多场景多普勒定位解算方法[J].无线电工程,2017,47(11):49-53.[DENG Zhixin,GAO Hong,WANG Libing.Mutiple-scene Doppler Locating Method for LEO Satellite Navigation System[J].Radio Engineering,2017,47(11)：49-53.]

2017-04-18

“十三五”国家重点研发计划基金资助项目(2016YFB0502402)。

高宏男，(1979—)，硕士，工程师。主要研究方向：卫星导航、大地测量。