金属柱状体工件内缺陷超声检测的特征分析*

陈友兴，吴其洲，刘蔺慧，高 捷

（1.中北大学仪器科学与动态测试教育部重点实验室，太原 030051；2.中北大学信息与通信工程学院，太原 030051）

金属柱状体工件内缺陷超声检测的特征分析*

陈友兴1，2，吴其洲2，刘蔺慧2，高 捷2

（1.中北大学仪器科学与动态测试教育部重点实验室，太原 030051；2.中北大学信息与通信工程学院，太原 030051）

超声技术是检测金属柱状体工件内部缺陷的常用方法，但是在缺陷的重构和类型识别方面还缺乏有效的方法。针对超声检测金属柱状体工件内部缺陷的情况，研究单个圆周截面上360°检测得到回波信号特征的分布规律。为了深入全面地分析规律普遍性，采用ansys仿真软件得出不同情况下仿真回波信号，并经证实仿真回波有效；结合实际的缺陷类型和缺陷回波特点，分析了不同位置圆形、椭圆形、矩形缺陷的仿真回波信号幅值和时间延时的规律，为进一步的缺陷识别和重构奠定基础。

缺陷检测，柱状体，超声检测，ansys仿真

Abstract：Ultrasonic technology is a common method to detect the internal defects of metal cylinder.However，there is still a lack of effective methods in the reconstruction and type identification of defects.In order to detect defect in metal cylindrical object more effectively，the circumferential distribution of the echo signal characteristics with 360 degree in one circular cross section is studied.In order to deeply and comprehensively analyze the regularity of the general，ANSYS software is used to simulate the echo signal of different defects，and it is proved being effective.Combining with the actual defect types and defect echo characteristics，the amplitude and time delay of the simulated echo signal with different positions of circular，elliptical and rectangular defects are analyzed，which lays the foundation for subsequent defect recognition and reconstruction.

Key words：defect detecting，cylindrical object，ultrasonic testing，ansys

0 引言

金属柱状体工件广泛应用于各个领域中，如汽车的零部件、武器装备中的弹体以及机械装备中的连接轴等。这些工件一般由原料经铸造或温挤工艺制作成坯料，再经其他工艺加工成产品。在坯料制作过程中，由于工艺和原材料的原因会造成产品内部存在气泡、裂纹、夹杂等缺陷，这些缺陷势必会影响到产品的最终使用，因此，在生产过程中或者产品出厂前需要对其检测［1-3］。现有的方法主要通过超声检测，除了检测工件内部是否存在缺陷外，有些场合还要求对缺陷进行类型分类、重构和尺寸计算。

关于柱体内缺陷的超声检测，在2006年～2012年期间北京工业大学采用born近似和Kirchhoff近似开展了方形孔、槽型、圆形孔的缺陷模型的仿真、理论模型和重构技术研究［4-6］，从机理上看上述的方法只能适用于某种形状（如圆或方形）的缺陷，并不适用于实际，近年来也没有见到后续的报道。浙江大学针对金属材料小缺陷，研究了散射模型和缺陷定位技术［7］。本课题组近几年来也开展柱状体声场仿真、缺陷检测和重构技术研究［8-10］，k-wave是一种比较新的仿真重构方法［11］，但是该方法与前面的born和Kirchhoff近似一样，是基于模型分析的，实际适用性不强；边界轮廓线的方法能够实现实际任意形状缺陷的重构，但是边界的准确确定是本方法的关键问题［9］；国外近几年关于柱状体方面检测报道相对较少，主要集中在声场和传播特性分析［12-14］；虽然医学重构方法可以应用于工业中，但是医学成像也存在不易进行缺陷边界确定和类型识别的问题［15-17］。

1 缺陷回波信号分析

1.1 实际检测缺陷回波

采用本实验室自行研制的超声自动检测系统［18］，对金属柱状体工件进行超声检测数据采集，以图1的工件为例，直径100 mm铝柱状体，在离中心25 mm处有一个直径为4 mm的孔缺陷，当探头移动到工件正下方时，探头不动，工件每旋转1°采集一个回波信号，一圈共采集360个信号。图1显示了工件旋转过程中，探头与缺陷的相对位置变化情况，图中相对运动中探头到达A（B）位置时，声束远方（近方）垂直入射到缺陷表面。图2是采集一个圆周截面的B扫描图，图3是探头正对缺陷的回波信号。

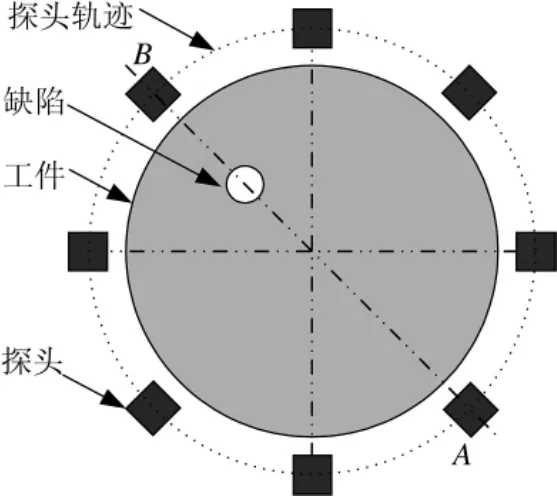
图1 工件及检测示意图

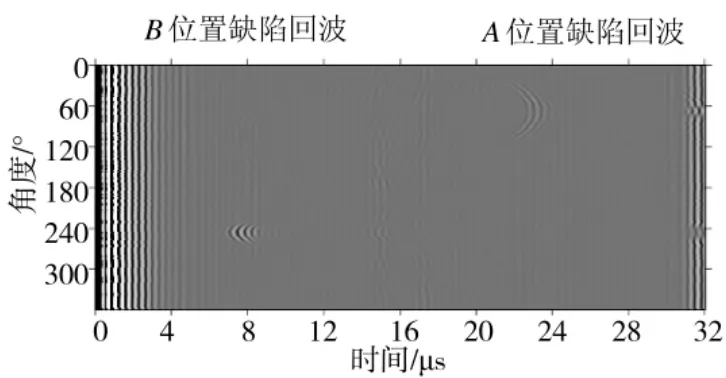
图2 一圈检测回波信号的B扫描图

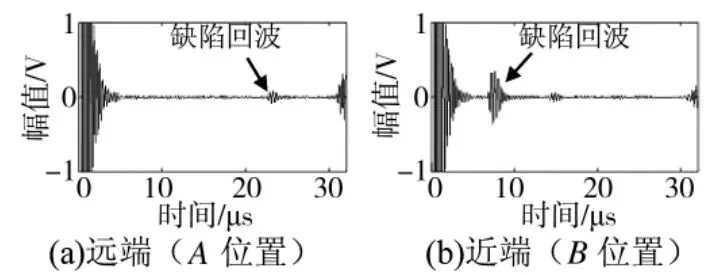
图3 探头正对缺陷时的检测回波信号

从图2可以看出，探头正对着缺陷时会有较大的缺陷回波信号，随着探头的偏移，缺陷回波的幅度和位置也在发生变化，随着探头的偏移角度增大，回波幅值也越来越小直到没有，在近端（B位置）附近，回波越来越靠后，在远端（A位置）附近，回波越来越靠前。图2所表现的现象主要是由于探头发射和接收回波时存在一定扩角度，所以在探头不是正对缺陷时也会存在缺陷回波，但是在偏离很远（角度很大）时，此时理论上的回波信号很小，因此，采集卡是采不到的。一周中缺陷回波的变化规律与缺陷的形状、位置、尺寸有关。

1.2 基于ansys的缺陷回波仿真

ansys是基于有限元分析的计算分析软件，利用其瞬态动力学单元，可以模拟超声波在传播过程中的应力应变情况，从而达到模拟超声波传播过程，并获取回波信号。图4是模拟图1工件得到的仿真回波信号B扫描图。

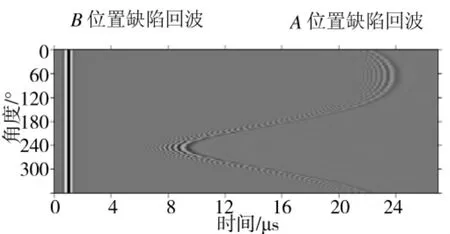
图4 仿真回波信号的B扫描图

仿真时的网络单元长度和时间步长遵循有限元网络细分原则［19］：

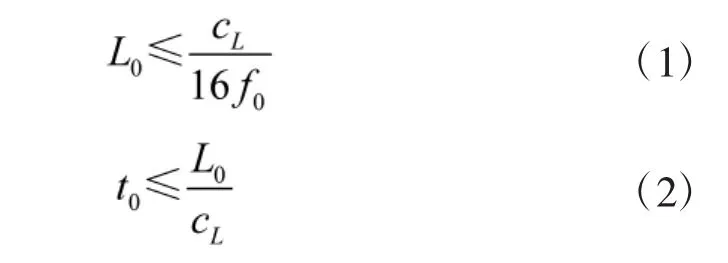
式中，L0为网格单元长度，t0为时间步长，cL为声速，f0为激励信号的中心频率。

从图4的仿真结果可以看出，本文的方法能够很好地仿真柱状体内缺陷的超声检测，规律与图2基本相同。为了进一步说明ansys软件有限元仿真的有效性。下页图5列出了实际采集信号和仿真回波信号缺陷特征回波的幅值和时间延时信息，为了方便比较图5（a）中的仿真信号回波幅值是经过比例放大以后的。

从图5中可以看出，探头在A位置和B位置附近所得到特征回波的规律基本一致，不同之处在于，仿真信号在探头角度偏离比较大时仍然有信号，主要原因是采用有限元仿真时激励信号是一个点源，没有方向性。但角度偏离大时，缺陷回波信号很小，不影响与实际信号的对比分析。

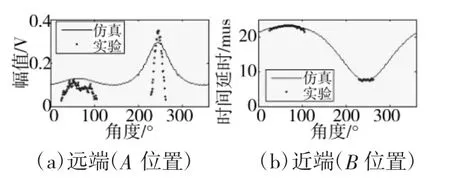
图5 仿真回波信号

2 缺陷回波信号的特征分析

2.1 圆形缺陷回波信号的特征分析

图6是针对不同位置、直径为10mm的圆形缺陷采用第1节的ansys仿真方法得到的回波幅值和时间延时。图中的4条曲线分别代表缺陷中心与工件中心的距离为0mm、10mm、18mm、20mm时的情况。

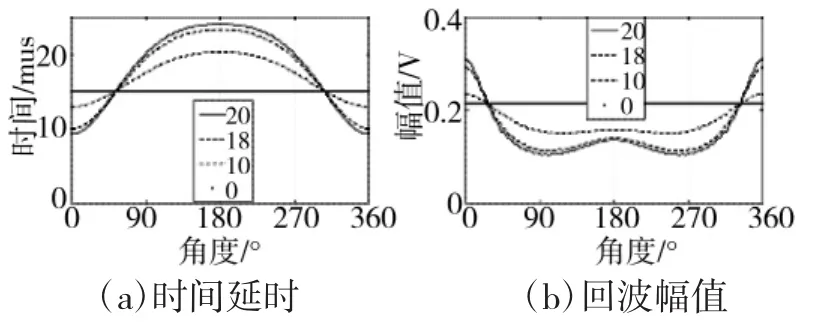
图6 不同位置圆形缺陷的特征分布

由图6可以看出，对于偏离中心的缺陷，探头在缺陷近端（图1的B位置，仿真是以该位置为起始0°）时回波最大，当探头向两边移动时，回波幅值会随着减小，当探头移动到远端（图1的A位置，图6的180°）时，回波幅值又会出现一个极大值，但是幅值会比0°的小。如果考虑周期性，图中的曲线以0°、180°偶对称，回波幅值的谷底在90°和270°处。缺陷偏离中心越远，上述的变化规律越明显，反之，变化趋势越趋于平趟，当缺陷在正中心时，探头在任意位置的回波幅值都一样。

2.2 椭圆形缺陷回波信号的特征分析

由于椭圆是有方向的，本文先按圆形的方法进行分析，图7是3个相同椭圆缺陷（尺寸相同、方向相同，短轴与直径重合）不同位置一周的探测回波幅值和时间延时曲线。椭圆缺陷的长轴为10 mm，短轴为5 mm。缺陷中心与工件中心的距离分别为 0 mm、10 mm、20 mm。

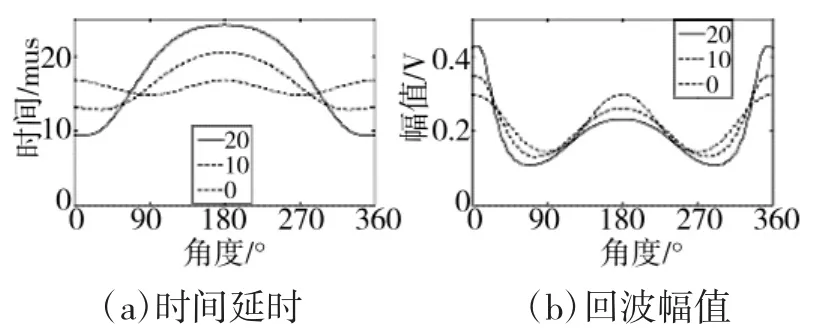
图7 离中心不同距离的椭圆形缺陷特征分布

从图7中可以看出，一圈回波信号幅值规律与圆形基本一样，但是幅值的谷底（图7（b））并不在90°方向，缺陷越偏离中心，谷底越靠近0°方向。缺陷在正中心时，谷底刚好在90°方向，这个结论似乎不合逻辑，因为中心缺陷的90°方向正是长轴的位置，此时超声波正对缺陷（曲率最小处）入射，缺陷回波理应较高，但却最低。其实回波除了和入射方向有关外，还和入射表面有关，对于椭圆来说，长轴对应位置的曲率最小，实际被探头接收到的反射回波是最少的，因此，其回波没有想象的那么大。当然这里还存在另一个原因，就是1.2节所述的，采用ansys仿真时由于没有考虑探头的方向性，把本来不是正对缺陷处的回波信号也有所加大。

由于椭圆形状具有方向性，本文还研究了其他位置缺陷的回波情况，图8（a）所示的位置，图中椭圆的长轴为5 mm，短轴为2.5 mm，4个缺陷（A、B、C、D）的中心是边长为10 mm的正方形的顶点，缺陷A的中心与工件A的中心重合。

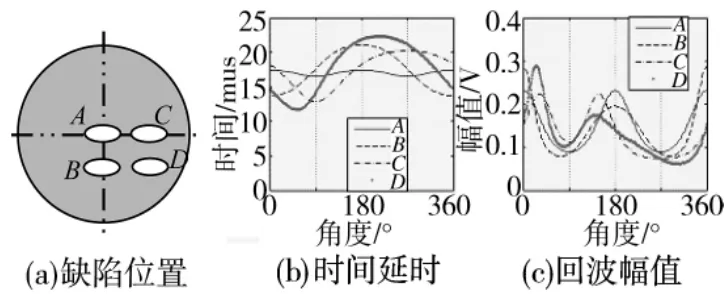
图8 不同位置椭圆形缺陷的特征分布

从图8的4条曲线比较发现，曲线A、B、C还有一定的规律，呈一定的对称性，在0°和180°附近幅值较大，而曲线D就基本上找不出相应的规律。因此，对于椭圆形缺陷的长轴或短轴与工件直径重合的情况（A、B、C），可以通过一周回波的幅值或时间延时曲线分析其缺陷特征；但对于其他位置（即长轴方向与工件直径成一定角度）的椭圆形缺陷所呈现的规律就很复杂。本课题组将继续研究更多位置的缺陷的特征，以分析其规律性，为气泡缺陷分析提供更加全面的依据。

2.3 矩形缺陷回波信号的特征分析

图9是不同位置正方形缺陷的回波幅值和时间延时分析。正方形缺陷边长为10 mm，缺陷中心分别距离工件中心0 mm、5 mm、15 mm、20 mm。

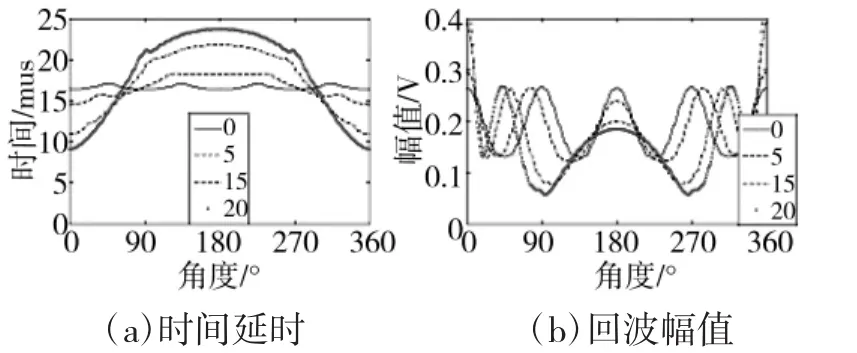
图9 不同位置方形缺陷的特征分布

从图9中可以看出，当探头正对正方形的边时，回波幅值最大，并形成一个一个的波峰。从图9（b）看，远端的波峰持续时间长，近端持续时间短，但峰值相对较大，这个与图6圆形缺陷的规律类似。

图10是中心长方形缺陷，缺陷长度不同所得到的回波规律。从图10可以看出，缺陷回波随着缺陷长度的增加而增加。

图10 不同长度矩形缺陷的特征分布

矩形缺陷与椭圆形缺陷类似，也存在方向性，本课题组将继续研究更多情况矩形缺陷的特征，为夹杂、裂纹缺陷分析提供更加充分的依据。

3 结论

本文针对金属柱状体工件内部缺陷的超声检测回波信号，分析了一个截面360°探头的回波信号，并通过ansys仿真软件，分析了不同缺陷形状、位置的仿真缺陷回波幅值和时间延时的规律，得出如下结论：

①不同的缺陷一周的回波信号呈现了不同的规律，在实际的缺陷检测中可以利用这一特点对缺陷进行分类和缺陷重构；

②由于椭圆形和矩形都具有方向性，因此，如果要得到更加全面的缺陷情况，还要作进一步的分析，由于超声是高频信号，采用ansys仿真时，需要很多的网格和很细的时间步长，仿真速度慢，又由于本文的分析方法，每种缺陷情况需要仿真360组数据，整体仿真速度很慢。如果要得到更加全面、更多类型缺陷的特征分布，还需要课题组长期不懈地仿真和分析。

③采用ansys仿真软件可以仿真超声检测的回波信号，仿真回波信号的规律与实际缺陷回波的规律在主要特征分布上是相同的，但由于采用ansys软件进行仿真时，没有考虑超声探头的扩散角问题，造成实际没有反射回波区域也有反射回波，对于分析复杂特征缺陷（椭圆、矩形在不同位置、不同角度）规律性造成一定的影响，因此，在实际应用中应该克服这些问题，这也是本课题组进一步研究的内容。

［1］戚励文，金永，王召巴，等.合金弹体棒状坯料超声检测方法研究［J］.弹箭与制导学报，2009，29（4）：269-272.

［2］金永，王召巴，丁战阳，等.一种小口径火箭弹弹头超声检测方法［J］.固体火箭技术，2010，33（1）：115-118.

［3］陈友兴，吴其洲，赵建辉，等.合金火箭弹弹体缺陷超声自动检测及信号处理［J］. 固体火箭技术，2013，36（5）：706-710.

［4］吴斌，郑钢丰，何存富.用Kirchhoff近似法对杆中球型缺陷的重构［J］. 应用基础与工程科学学报，2007，15（1）：97-103.

［5］吴斌，郑钢丰，何存富.用二维逆born近似法对杆中方形缺陷的重构 ［J］. 北 京工业大学学报，2007，33（3）：229-234.

［6］郑钢丰，吴斌，何存富.用改进的Kirchhoff方法重构非均匀介质中缺陷形状 ［J］. 压电与声光，2012，34（1）：118-120.

［7］叶钱.噪声背景下金属材料小缺陷超声检测关键技术的研究［D］.杭州：浙江大学，2015.

［8］陈友兴，席海军，郭文静，等.基于多元高斯声束模型的圆柱体三维声场仿真［J］.火力与指挥控制，2015，40（6）：140-144.

［9］肖兆骞，陈友兴，任阳山，等.基于体绘制的圆柱体构件缺陷三维重构方法［J］. 火力与指挥控制，2015，40（3）：22-25.

［10］李雅，陈友兴，任阳山，等.基于k-wave超声场时域仿真研究［J］.电子技术应用，2015，41（11）：132-134+139.

［11］BRADLEY E.TREEBY B T，Cox.k-Wave.MATLAB toolbox for the simulation and reconstruction of photoacoustic wave fields［J］.Journal of Biomedical Optics，2010，15（2）：021314（1-12）.

［12］WANG J T，JURG D.Theoretical and numerical calculation of the acoustic radiation force acting on a circular rigid cylinder near a flat wall in a standing wave excitation in an ideal fluid［J］.Ultrasonics，2012（52）：325-332.

［13］LIN C I，LU Y，HE C F.Cylindrical rayleigh surface waves on a layer-coated cylinder measured by PVDF transducer and defocusing measurement method［J］.NDT&E International，2015，（74）：43-49.

［14］RAJAGOPAL P，PATTANAYAK R K.Ultrasonic guided waves in elliptical annular cylinders［J］.Acoust.Soc.Am.，2015，138（3）：EL336-341.

［15］COATRIEUX J L，VELUT J，DILLENSEGER J L，et al.From medical imaging to image-guided therapy［J］.M S-Medecine Sciences，2010，26（12）：1103-1109.

［16］ZADICARIO E，RUDICH S，HAMARNEH G，et al.Image-based motion detection using the concept of weighted directional descriptors［J］.IEEE Engineering in Medicine and Biology Magazine，2010，29（2）：87-94.

［17］WEN Q N，WAN S R，LIU Z L，et al．Ultrasound contrast agents and ultrasound molecular imaging ［J］.J Nanosci Nanoteehn01，2014，14（1）：190-209.

［18］陈自立，陈友兴.圆锥形物体超声自动检测系统设计［J］.计算机测量与控制，2013，21（11）：2947-2949.

［19］王勖成.有限单元法［M］.北京：清华大学出版社，2003.

Ultrasonic Characteristics of Defects in Metal Cylindrical Object

CHEN You-xing，WU Qi-zhou，LIU Lin-hui，GAO Jie
（1.Key Laboratory of Instrumentation Science and Dynamic Measurement，Ministry of Education，North University of China，Taiyuan 030051，China；2.School of Information&Communication Engineering，Taiyuan 030051，China）

TP23

A

10.3969/j.issn.1002-0640.2017.09.035

1002-0640（2017）09-0158-04

2016-08-08

2016-09-19

国家自然科学基金（61201412）；山西省青年科技研究基金（2012021011-5）；山西省青年学术带头人计划资助项目

陈友兴（1978- ），男，福建福安人，博士，副教授。研究方向：超声检测及信号处理。