固定舵二维弹道修正组件结构模型*

朱少雄，施冬梅

（军械工程学院，石家庄 050003）

固定舵二维弹道修正组件结构模型*

朱少雄，施冬梅

（军械工程学院，石家庄 050003）

为了满足二维弹道修正组件小型化设计要求，设计了3种二维弹道修正组件模型，应用SolidWorks软件和ICEM软件分别建立3种修正组件的实体模型和网格模型，并利用Fluent软件进行气动特性数值计算，将计算结果进行对比分析，得出不同修正组件模型参数对气动特性的影响。研究结果表明，修正组件尺寸的减小会增大阻力系数；舵片形状和尺寸对阻力系数和升力系数影响较小，但是对滚转力矩系数影响较大，矩形结构的舵片对舵片周围气动特性会产生不利影响；在满足修正要求的前提下，可以适当缩小舵片面积来降低舵机控制难度，提升飞行稳定性。

固定舵，二维弹道修正组件，舵片结构，气动特性

Abstract：In order to meet the design requirements of two-dimensional trajectory correction fuse miniaturization，three models of two-dimensional trajectory correction component are designed in this paper.Solid models and mesh modes of two-dimensional trajectory correction fuse are established by SolidWorks and ICEM software.By using Fluent software，the aerodynamic characteristics values of different correction component models are gained.By comparing the aerodynamic characteristics values ofthethree models，the influence ofdifferentcorrection componentmodelson aerodynamic characteristics is obtained.The result shows reduce the length of correction component will increase the drag coefficient.The rudders’shape and size have little effect on lift and drag coefficient while have larger effect on roll damping moment coefficient.Under the conditions of meeting the correction requirement，the area of rudder can be appropriately decreased to reduce the difficulty of steering control and improve the flight stability.

Key words：fixed canard，two-dimension trajectory correction component，rudderstructure，aerodynamic characteristic

0 引言

在现代战争中，精确制导弹药发挥着极其重要的作用，各国为了提高精确打击能力、减小作战成本，对二维弹道修正弹进行了深入的研究，世界范围内涌现出了各种各样的概念和研究思路，各国研究人员对不同原理、不同结构的二维弹道修正弹进行了相应的研究［1-3］，对二维弹道修正弹的发展作出了突出贡献。文献分析了固定鸭舵的不同气动布局对弹丸气动特性的影响。文献［5］研究了鸭式布局弹箭的阻力、升力、俯仰力矩等气动参数随攻角、侧滑角、马赫数等参数变化的规律。文献［6］研究了舵片位置、形状等参数对火箭靶弹气动特性的影响，得出了控制效率较高、升阻比较大的舵片结构参数。文献［7］以加装不同舵偏角鸭舵的普通制式弹丸为研究对象，对不同舵偏角的舵片结构进行了研究。文献［8］研究了修正机构位置对弹丸气动特性及弹道特性的影响。文献［9］分别对155 mm制式弹和采用Course Correction Fuze（CCF）模式的二维弹道修正弹进行气动特性分析，分析了两种弹丸的弹道特性。

在普通弹丸上加装修正组件会对原本弹丸的气动特性产生一定影响，进而影响到弹丸的弹道特性。国内学者主要研究了舵片结构参数、安装位置和角度对气动特性的影响，并没有进一步研究修正组件长度尺寸对修正弹气动特性的影响。为了对比修正组件尺寸和舵片结构对修正弹气动特性的影响，本文在某制式弹药的基础上，建立了3种加装不同尺寸结构二维弹道修正组件的修正弹实体模型。根据建立的实体模型，应用计算流体力学的软件进行数值计算，得到不同结构下的气动参数。通过对比不同修正组件结构的气动参数，对比不同修正组件结构的流场特性，分析不同修正组件结构对气动特性的影响，为下一步进行弹道特性分析提供气动依据。

1 实体模型

以某制式弹药为原型，通过在头部加装修正组件替代原头部组件来构建不同的模型，实体模型如图1。其中图1表示模型I，该模型尺寸与制式弹一致，修正组件相比原制式弹药引信部分未缩短，舵片截面为菱形；图2表示模型II，该模型修正组件缩短15 mm，舵片截面为菱形，模型I舵片面积比模型II大10%左右；图3表示模型III，其修正组件缩短15 mm，舵片截面为矩形，模型II和模型III舵片后掠角、舵片面积基本相同。

图1 实体模型I

2 网格模型

图2 实体模型II

图3 实体模型III

根据第1节建立的实体模型，应用ICEM软件对其进行网格划分，得到的网格模型如图4、图5。各个模型在网格生成过程使用相同的方法，最终生成的网格数量基本一致。图4、图5为模型I的网格模型，图6、图7为模型II的网格模型，图8、图9为模型III的网格模型。3个模型外流场网格基本相同，只在舵片周围有所区别。生成的网格模型在舵片和弹体周围进行了加密并建立了边界层棱柱网格，保证在计算过程中的精确度［10］。

图4 模型I弹体网格

图5 模型I对称面网格

3 气动特性分析

应用Fluent软件对不同网格模型进行计算，计算条件和设置相同。通过对不同网格模型进行数值计算，得到不同修正组件结构修正弹的气动参数。Fluent设置如下［11］：

图6 模型II弹体网格

图7 模型II对称面网格

图8 模型III弹体网格

图9 模型III对称面网格

1）求解器选择密度求解器（Density-Based），能够适用于超声速流场的计算；

2）计算域流场边界条件选取Pressure-Far-Field，流体物质选择Idea-Gas，气压P=101 325 Pa、温度T=300 K、密度 ρ=1.225 kg/m3；

3）湍流模型选择 S-A 模型（Spalart-Allmaras），适用于航空领域的计算，能够减小计算时间；

4）残差收敛标准设置为0.000 1，收敛因子初始值均设置为0.1，根据计算过程中残差变化进行调整。

3.1 CFD数值方法

CFD数值方法是通过求解N-S方程来求解气动问题［12］。Fluent软件采用的是有限体积法。有限体积法的基本过程是：将计算区域划分为有限个连续的网格，使每个网格节点的周围存在一个互不重复的控制体积，然后在每一个控制体积上对微分方程进行积分，求解积分形式的守恒方程为：

利用高斯公式可以转化为：

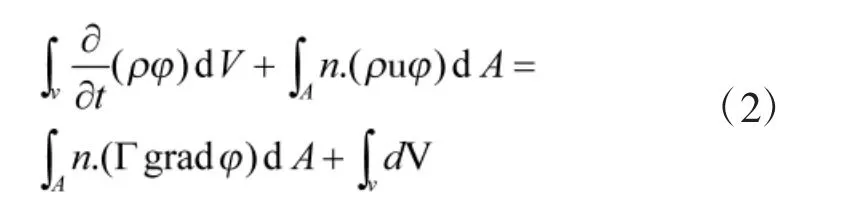
式（2）等号左边第1项表示变量φ的总量在控制体积内随时间的变化量，左边第2项表示变量φ因对流而引起的沿控制体积表面外法线方向n的流出率。右边第2项是扩散项的积分，物理意义就是控制体积内变量因扩散而引起的净增加量。

3.2 风洞试验验证

为了确定计算所得数据的有效性，需通过风洞试验验证Fluent软件设置是合理可信的。本文对侧滑角为 0°，马赫数为 2.5，攻角为 -2°、0°、2°和4°的弹体模型进行计算，将得到的阻力系数Cd与风洞试验数据进行对比。数值计算结果与风洞试验数据结果如表1、图10所示。

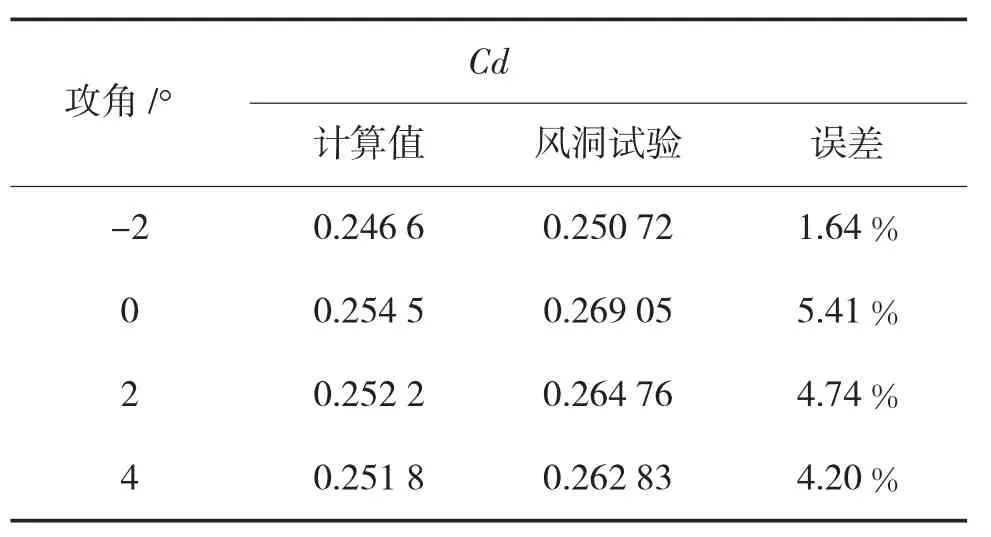
表1 不同攻角下阻力系数计算值和试验值

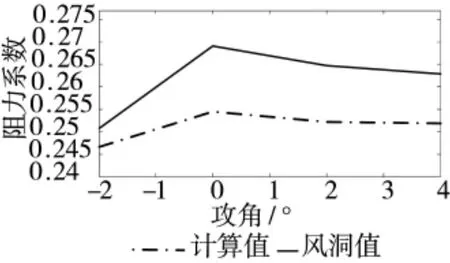
图10 阻力系数对比曲线

根据表1和图10可知，计算值与风洞试验数值最大误差为5.41%，说明计算得到的数据和风洞实验数据相符，且计算得到的阻力系数随攻角变化规律与试验基本吻合，说明建立的气动模型和Fluent设置是合理可信的，可以应用到以后的仿真计算。

3.3 阻力系数

根据Fluent计算结果，选取攻角为0°时气动数据进行分析。3种模型的阻力系数与马赫数的关系如图11所示。由图可知，3种模型阻力系数曲线变化规律相同，均在1.2 Ma附近达到最大值。出现这种现象是因为在跨声速阶段，弹体周围出现局部激波［13］，阻力系数逐渐上升。随着马赫数的继续增大，弹体周围激波逐渐趋于稳定，阻力系数缓慢减小。由图11可以看出，模型I的阻力系数最小，模型III的稍大，模型II的最大。这是因为模型I的修正组件长度未缩短，如图12所示，面1和面2处的曲面比较平缓，因此，模型I的阻力系数较小，曲线趋势较平缓。而模型II和模型III的修正组件长度均缩短了15 mm，面1和面2处的曲面较陡，因此，模型II和模型III的阻力系数较大，且曲线斜率较大。模型II和模型III舵片结构不同，模型II的舵片截面为菱形，模型III的舵片截面为矩形，模型II舵片与来流接触面积更大一些，因此，模型II的阻力系数比模型III的大，模型II、模型III与模型I的偏差如表2所示。

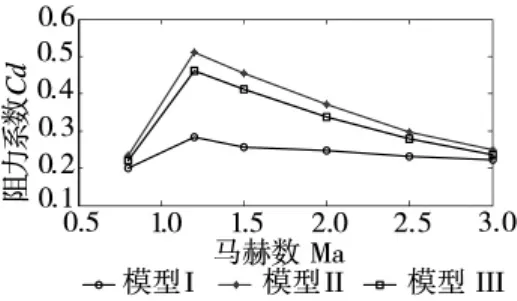
图11 阻力系数与马赫数曲线

图12 弹体头部结构

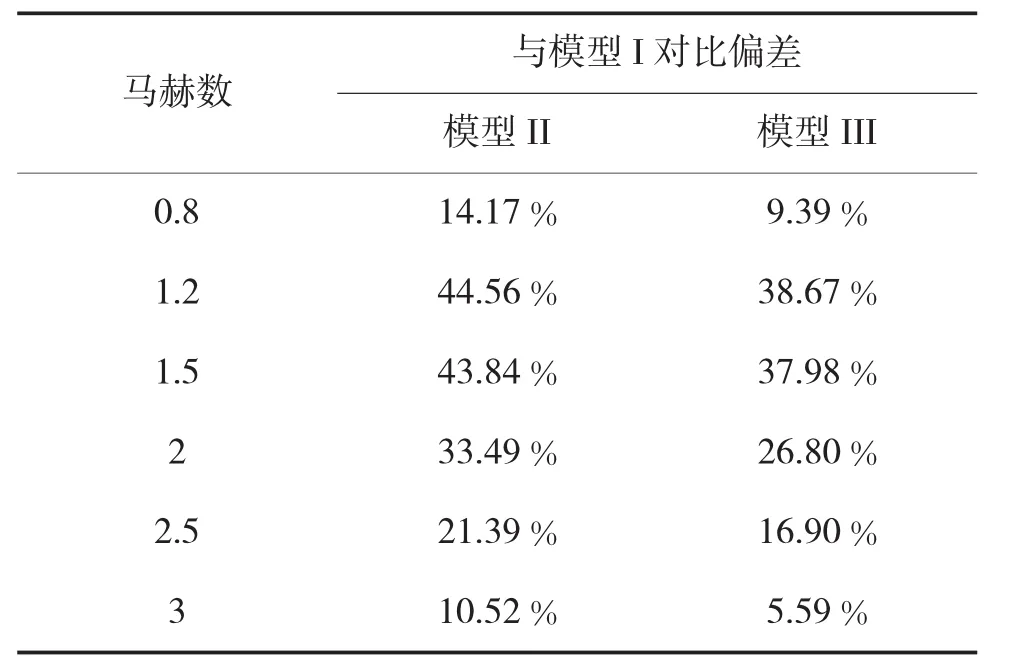
表2 阻力系数偏差

3.4 升力系数

根据Fluent计算结果，选取1.5 Ma时气动数据进行分析，对比升力系数与攻角的关系，并分析升阻比。3种模型的升力系数与攻角的关系如图13所示，可以看出，3种模型升力系数均与攻角呈线性关系［14］，且模型I变化率最大，模型II次之。在马赫数一定的情况下，升力系数主要与攻角有关，并与攻角呈线性关系。因模型I舵片比模型II稍大，因此，模型I升力系数比模型II稍大，而模型III舵片截面为矩形，舵片与来流接触角度比模型II稍小一些，因此，升力系数比模型III要小，模型II、模型III与模型I的升力系数偏差如表3所示。

图13 升力系数与攻角曲线

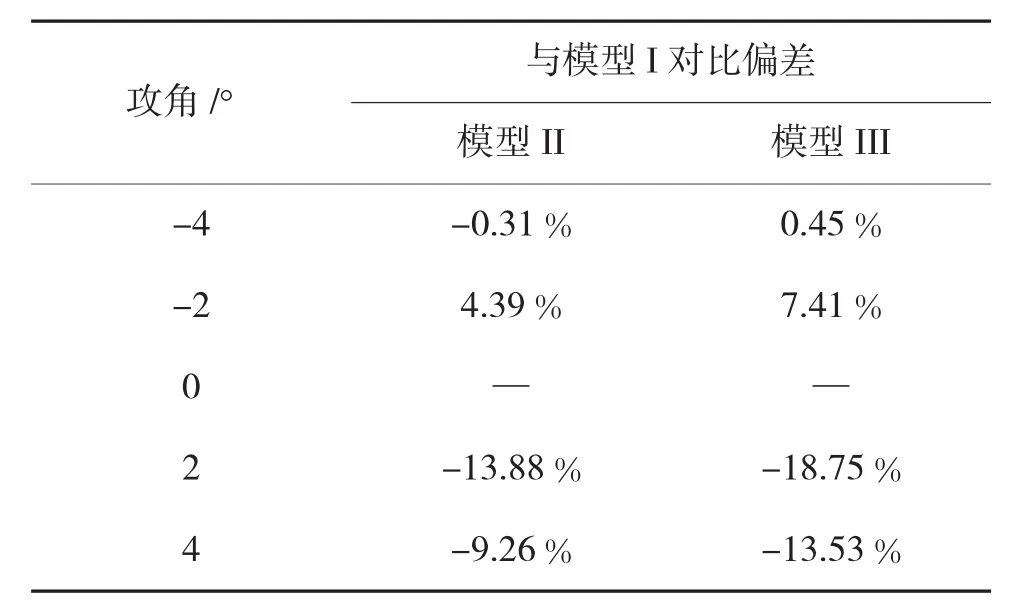
表3 升力系数偏差

3.4 滚转力矩系数

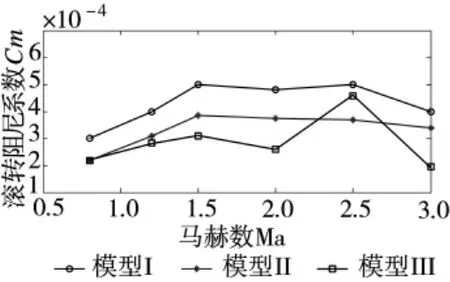
图14 滚转力矩系数与马赫数曲线

根据Fluent计算结果，选取攻角为0°时数据，对比3种模型的滚转力矩系数Cm。计算条件设置侧滑角为0°时，滚转力矩系数较小，如图14所示。从图14可以看出，模型I的滚转力矩在不同马赫数时都是最大的，而模型II的较小，变化趋势较平缓，模型III的滚转力矩变化幅度较大。模型I与模型II的滚准力矩系数变化规律基本一致，模型I比模型II稍大。这是因为模型I的舵片比模型II大，作用在舵片上的力也大一些，因此，滚转力矩系数比模型I偏大。而模型III的舵片形状与模型I和模型II不同，模型III的舵片截面为矩形，在不同马赫数下舵片上力的作用点与模型II不同，因此，模型III的滚转力矩系数变化与模型II不同。滚转力矩系数越大，对应的减旋控制时需要的力矩就会相应增大，对控制舵机的要求越高。因此，模型II的舵片结构对舵机要求较低。

3.5 流场特性分析

超声速流场中激波的捕捉往往是人们关注的重点之一。图15为模型I在马赫数为1.5时的流场压力云图，因3种模型仅头部修正组件尺寸结构不同，对整体流场影响不大，因此，流场压力云图基本相同，而弹体头部附近压力云图不同，如图16～图18所示。

从图15可看出，在弹体头部周围产生了一系列的压力激波，尾部产生了一系列的膨胀波，并在底部产生了明显的回流区并形成了低压区。由图16～图18可以看出舵片结构的不同会对头部周围流场产生一定的影响，菱形结构的舵片后方会产生较大的膨胀波，而矩形结构的舵片后方产生的膨胀波较小；3种模型的舵片前方均会产生压力激波，而矩形结构的舵片由于与来流接触面为非流线型壁面，边界层不能承受较大的逆压梯度，因此，出现了边界层分离。边界层分离可能会对修正弹的气动特性和操纵性能产生不利影响，因此，在选择舵片结构时，应该优先选择流线型结构，可在一定程度上减小阻力，避免激波振动、气动载荷振荡的现象。

图15 流场压力云图

图16 模型I头部压力云图

4 结论

图17 模型I头部压力云图

图18 模型I头部压力云图

为了满足小型化的要求，本文以二维弹道修正弹为基础模型对修正组件进行参数调整，得到固定舵修正组件的新结构。通过对不同舵片结构的固定舵二维弹道修正组件进行气动特性分析，研究了不同舵片结构、不同修正组件尺寸对二维弹道修正弹的气动特性影响。根据得到的计算数据，主要分析了3种模型的阻力系数、升力系数、滚转力矩系数和流场特性，通过分析得到以下结论：①缩短头部修正组件的尺寸会增大弹体头部曲面坡度，进而增大修正弹的阻力系数；②不同舵片形状对阻力系数、升力系数等气动参数均有一定影响，相同舵片面积条件下，舵片截面为菱形的修正组件比舵片截面为矩形的修正组件的阻力系数和升力系数都大一些；③不同舵片形状对滚转力矩系数影响较大，舵片截面为菱形的修正组件滚转力矩系数变化较平缓，舵片面积小的修正组件对舵机控制的要求较小；④采用矩形舵片形状会在舵片周围产生边界层分离现象，可能对舵片结构的稳定性和可操纵性产生不利影响。因此，在满足一定修正能力的前提下，可以优先采用舵片截面为菱形的修正组件，适当缩小舵片的面积，进而降低舵机的控制难度，使其满足二维弹道修正组件的小型化要求。

［1］张民权，刘东方，王冬梅，等.弹道修正弹发展综述［J］.兵工学报，2010，31（2）：127-129.

［2］邱荣剑，陶杰武，王明亮.弹道修正弹综述［J］.国防技术基础，2009，38（8）：7-9.

［3］赵金强，龙飞，孙航.弹道修正弹综述［J］.制导与引信，2005，26（4）：16-19.

［4］袁备，段智敏，陶迎迎.基于固定鸭舵高速旋转弹气动特性［J］.机电技术，2015，39（5）：42-49.

［5］屈贤琳.鸭式布局弹箭滚转飞行测偏问题的气动分析［D］.南京：南京理工大学，2010.

［6］程登华，曹红松.舵片形状对舵控火箭靶弹气动特性影响研究［J］.机电技术，2015，39（4）：68-71.

［7］邵盼，郭煜洋，郝永平，等.鸭舵修正机构舵偏角选择方法［J］.弹箭与制导学报，2014，34（6）：34-36.

［8］郝永平，郭煜洋，张嘉易.二维弹道修正弹修正机构气动布局研究［J］.弹箭与制导学报，2013，33（6）：121-124.

［9］HAMEL N，GAGNON E.CFD and parametric study on a 155mm artillery shell equipped with a roll-decoupled course correction fuze［C］//29th AIAA Applied Aerodynamics Conference.Honolulu，Hawaii，2011：243-252.

［10］纪兵兵，陈金瓶.ANSYS ICEM CFD网格划分技术实例详解［M］.北京：中国水利水电出版社，2012.

［11］王瑞金，张凯，王刚.Fluent技术基础与应用实例［M］.北京：清华大学出版社，2007.

［12］王友进，郑咏岚，张庆兵，等.基于CFD方法的典型防空导弹气动反设计研究［J］.现代防御技术，2011，39（2）：2-5.

［13］林建忠，阮晓东，陈邦国.流体力学［M］.北京：清华大学出版社，2013.

［14］李新国，方群.有翼导弹飞行动力学［M］.西安：西北工业大学出版社，2005.

［15］杨泗智，胡宽荣.远程火箭弹滑翔增程技术研究［J］.现代防御技术，2011，39（4）：16-18.

Research on Two-dimensional Trajectory Correction Component Structure with Fixed Canards

ZHU Shao-xiong，SHI Dong-mei
（Ordnance Engineering College，Shijiazhuang 050003，China）

TJ410

A

10.3969/j.issn.1002-0640.2017.09.039

1002-0640（2017）09-0175-05

2016-08-19

2016-09-27

军队武器装备预研基金资助项目（9140A05040114JB34015；9140A05040213JB34069）

朱少雄（1992- ），男，河北保定人，硕士。研究方向：二维弹道修正弹气动仿真。