一种多模型贝努利粒子滤波机动目标跟踪算法

杨 峰 张婉莹



一种多模型贝努利粒子滤波机动目标跟踪算法

杨 峰 张婉莹*

(西北工业大学自动化学院 西安 710129) (信息融合技术教育部重点实验室 西安 710129)

交互式多模型贝努利粒子滤波器(Interacting Multiple Model Bernoulli Particle Filter, IMMBPF)适用于杂波环境下的机动目标跟踪。但是IMMBPF将模型信息引入粒子采样过程中会导致用于逼近当前时刻真实状态与模型的粒子数减少，而且每次递推各模型间的粒子都要进行交互，存在计算量过大的缺点。为提升IMMBPF中单个采样粒子对于真实目标状态和模型逼近的有效性，该文提出一种改进的多模型贝努利粒子滤波器(Multiple Model Bernoulli Particle Filter, MMBPF)。预先选定每一个模型的粒子数，且模型间的粒子不需要进行交互，减少了计算负荷。模型概率由模型似然函数计算得到，在不改变模型的马尔科夫性质的条件下避免了小概率模型的粒子退化现象。仿真实验结果表明，所提出的MMBPF与IMMBPF相比，用较少的粒子数就可获得更优的跟踪性能。

机动目标跟踪；贝努利滤波；粒子滤波；多模型

1 引言

贝努利滤波器(Bernoulli Filter, BF)是随机有限集(Random Finite Set, RFS)框架下的一类最优序贯贝叶斯滤波器[1]。当考虑目标存在概率时，目标状态可建模为贝努利RFS。随机集统计学理论为统计描述和数学处理RFS随机变量提供了现实依据。目前，贝努利滤波主要应用于目标跟踪，传感器网络，虚拟跟踪和雷达监控等方面。

对于机动目标跟踪，文献[6]提出的交互式多模型 (Interacting Multiple Model, IMM) 算法得到了广泛的应用，然而IMM算法在系统模型高度非线性时滤波效果较差。粒子滤波(Particle Filter, PF)因其不受非高斯、非线性问题的限制而被众多学者研究推广。文献[7]将PF与IMM方法相结合，提出IMMPF算法，在非线性、非高斯系统中可获得良好的跟踪性能，文献[8]和文献[9]提出的IMMPF算法中粒子数没有参与模型切换，但是每次递推各模型间的粒子都需要进行交互，存在计算量过大的缺点，文献[10]提出用各模型的粒子权值总和去更新模型后验概率，在模型粒子数量差别较大时会使模型切换难以实现。

现有的针对机动目标跟踪的交互式多模型贝努利粒子滤波(IMMBPF)算法[11,12]，只是简单地结合IMM和BF的粒子实现方式，并为每一个模型分配大量的粒子，也能通过粒子的传播估计出目标状态，但对于线性、机动性较弱的模型来说，大量的粒子是不必要的，通常也会影响滤波性能，带来额外的计算负担。一般来说，我们更加关注非线性、机动性较强的模型，对于此类模型可适当地采用较多的粒子；而对线性、非机动的模型可以适当地减少粒子数。文献[13]指出在IMMPF算法中，为了有效逼近真实系统状态，应对主要模型分配较多的粒子数；文献[14]给出解决此类问题的一种新思路，即各模型的粒子数根据模型特性预先选定，并在递推过程中保持不变，且模型间的粒子不进行交互，减少了计算量。针对上述问题，本文提出一种改进的多模型贝努利粒子滤波(MMBPF)算法。

2 问题描述

给定如式(1)所示系统：

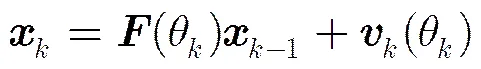
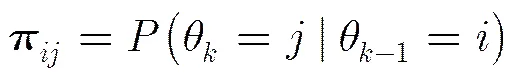
传感器提供目标的径向距离和方位角信息：

(4)

3 改进的多模型贝努利粒子滤波算法

3.1 改进的MMBF算法

多模型贝努利滤波算法适用于跟踪机动目标，它是将贝努利滤波与MM算法相结合。统计目标的可能运动模型，并为每种模型分配一个滤波器，各个滤波器并行工作，通过计算模型概率来评估模型的权重，综合输出来估计目标状态。

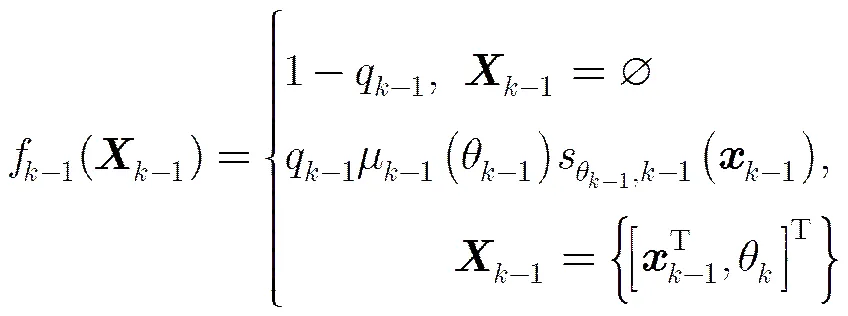
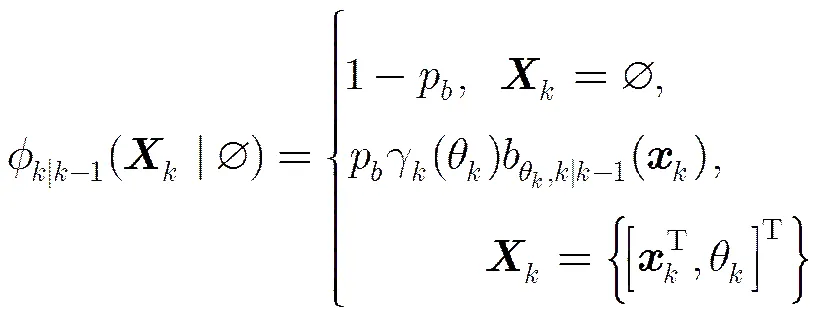
(7)

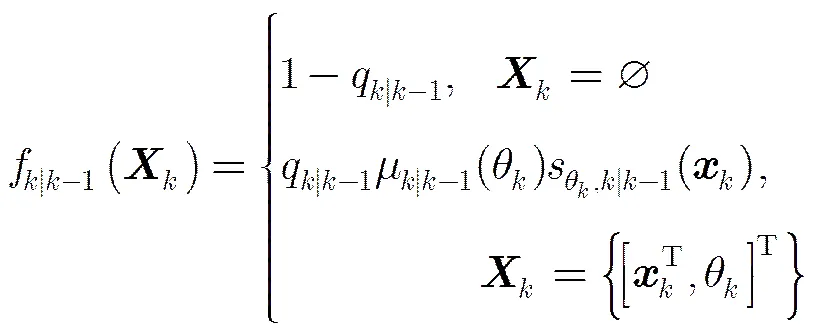
其中，

(9)

(11)

其中，

(13)

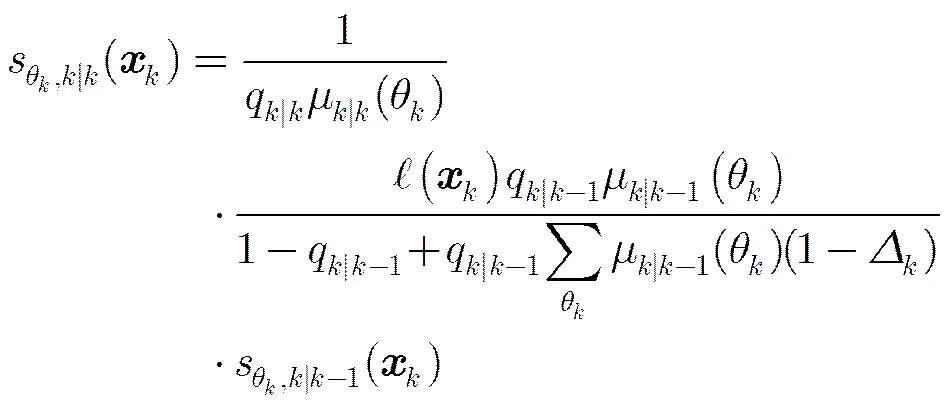
(15)

(16)

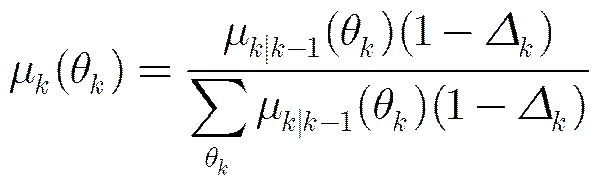
3.2 MMBF粒子实现方式

本文所提MMBPF算法与标准交互式多模型粒子贝努利滤波(IMMBPF)算法的不同之处是首先根据模型的机动性大小选择每个模型的粒子数。对于不同模型的固定粒子数目该如何确定，由于粒子数量不参与模型切换，模型概率由似然函数进行更新，可以独立控制各个模型的粒子数量，不影响模型的正常切换。本文采用一个较简单的方式选取各模型的粒子数：对非线性较强的模型，为了保证跟踪精度，用较多的粒子，以便更好地近似其状态后验概率密度；而对线性、机动小的模型采用较少的粒子，不影响跟踪精度，同时可以减少计算量。

下面将具体描述MMBPF算法的递归过程。

步骤1 计算各模型预测概率和混合概率：

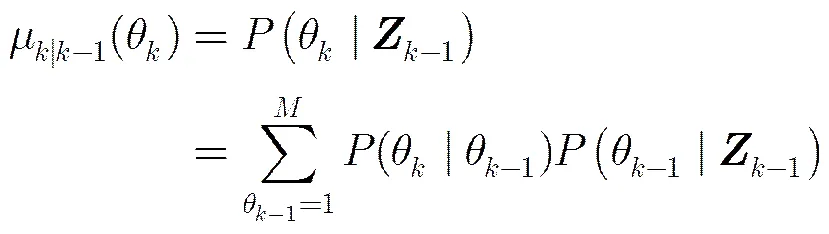
(19)

步骤2 初始化粒子群：本文算法在混合阶段不像传统IMMBPF那样对各模型的粒子进行交互计算，也不通过马尔科夫转移概率对各模型粒子进行重新分配。而是按照模型混合概率在上一时刻各模型滤波得到的后验粒子群中进行重采样，重建当前时刻模型的初始粒子群。本文采用类似于bootstrap滤波器中重采样的方法[10]，根据式(19)计算得到模型混合概率，通过概率采样确定个粒子上一时刻的模型索引，即它们分别来自上一时刻哪个模型的粒子群，然后按照模型索引在对应后验粒子群中随机抽取状态粒子给模型，获得时刻模型的初始化粒子群，其中代表模型的粒子数目。

步骤3 模型条件贝努利粒子滤波：

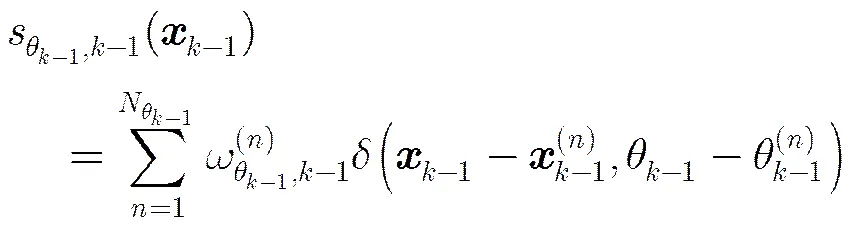
预测目标状态概率密度包括存活目标和新生目标两部分

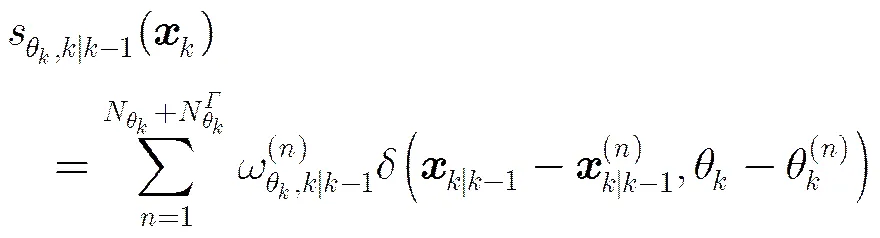
粒子从式(22)中两个建议分布密度函数中采样：

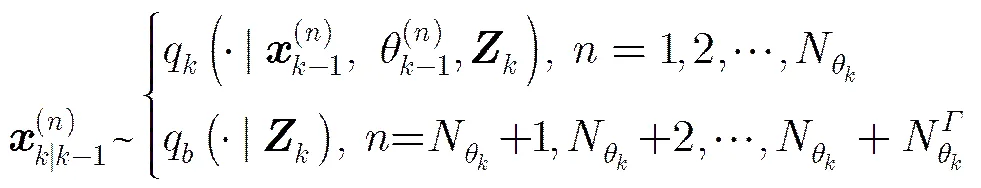
对应粒子权值为

(23)

权值归一化：

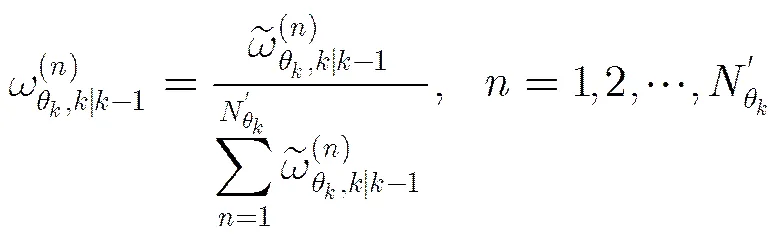
(2)更新：将式(21)代入式(15)，可得

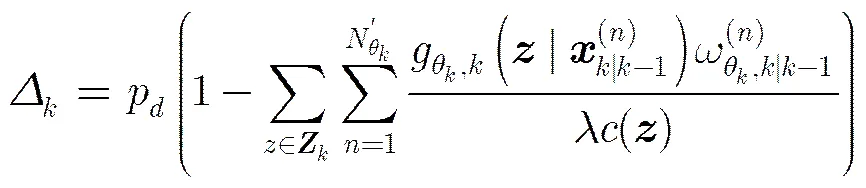
将式(25)分别代入式(13)和式(17)可得更新的目标存在概率和更新的模型概率。

将式(21)代入式(14)，可得

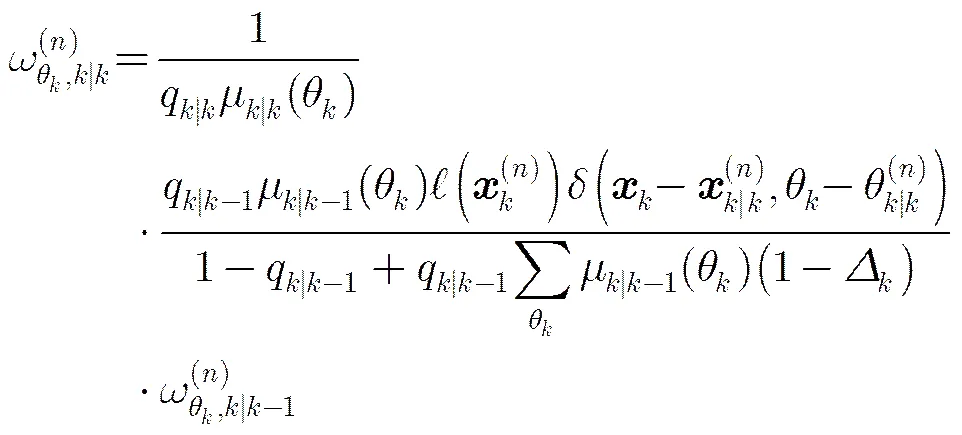
(27)

重采样后权重大的粒子，即对于目标真实状态逼近程度高的粒子被有效复制，小权值粒子被删减，重采样过程不仅实现了预测粒子的更新，同时有效改善了粒子退化现象的影响。

步骤4 输出状态估计

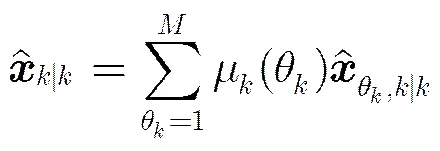
4 仿真验证

采用CV模型和CT模型对目标运动进行描述。

(1)CV模型：

(2)CT模型：

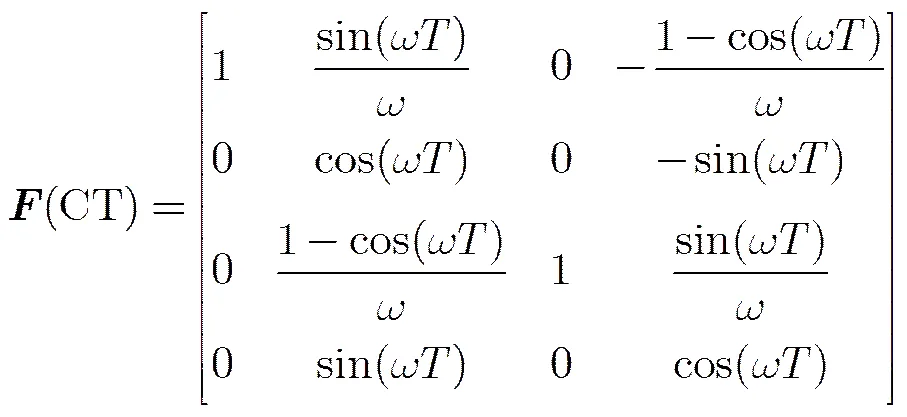
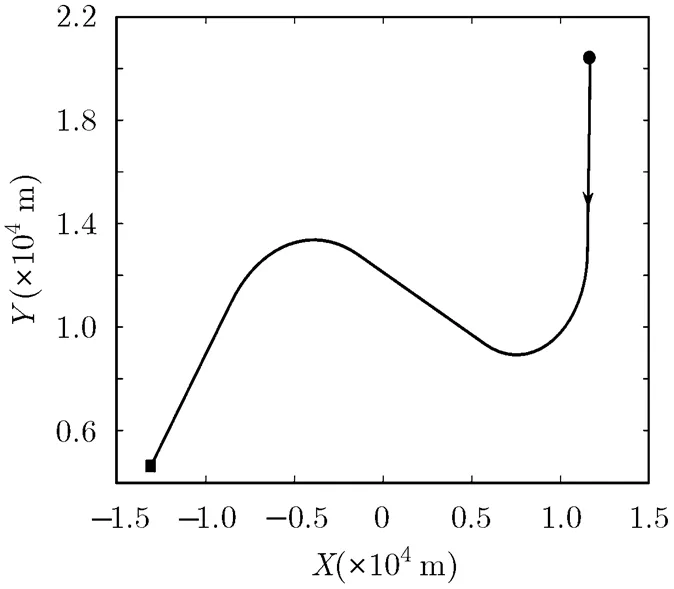
图1 目标真实运动轨迹(表示起点，■表示终点)

为了验证所提算法的性能，采用标准的IMMBPF算法[11]与所提算法MMBPF进行对比分析。仿真平台参数：CPU主频3.3 GHz, 8 GB RAM，仿真软件：Matlab R2014a。

(1)粒子总数相同时滤波性能对比：采用与文献[11]相同的粒子个数。IMMBPF和MMBPF每个模型使用1000个粒子。蒙特卡洛仿真50次，图 2，图 3分别为位置RMSE和速度RMSE对比图。可以看出，在机动目标跟踪过程中，MMBPF比IMMBPF有更高的位置和速度估计精度，同时由表1平均运算时间对比数据可以看出，本文所提的MMBPF算法要稍快于IMMBPF，说明各模型粒子之间没有进行交互会减少计算量。

(2)粒子总数不同时滤波性能对比：由于CV运动的线性特性，用较少的粒子数就可逼近真实的运动状态，因此减少MMBPF粒子数，CV模型使用300个粒子，两个CT模型各使用700个粒子。IMMBPF粒子数维持不变，50次蒙特卡洛仿真对比结果：表 2为平均运算时间对比，图 4，图 5分别为位置估计和速度估计RMSE曲线。可见MMBPF所用粒子总数约为IMMBPF的一半，但整体跟踪精度仍然要优于IMMBPF。

表1 平均运算时间对比(s)

算法平均运算时间 IMMBPF0.2799 MMBPF0.2618

表2 平均运算时间对比(s)

5 结论

本文提出的改进的多模型贝努利粒子滤波算法(MMBPF)，能够根据模型特性控制每一个模型的粒子数量，对机动性强的模型采用较多的粒子数，机动性弱的模型采用较少的粒子数，可以有效地提高粒子的利用率，且模型间的粒子不进行交互，减少了计算量，目标的状态估计和模型概率更新分开进行，利用模型的似然函数更新模型后验概率。仿真结果表明，所提出的多模型贝努利粒子滤波算法用较少的粒子总数就可获得更优的跟踪性能。

图2 位置RMSE曲线

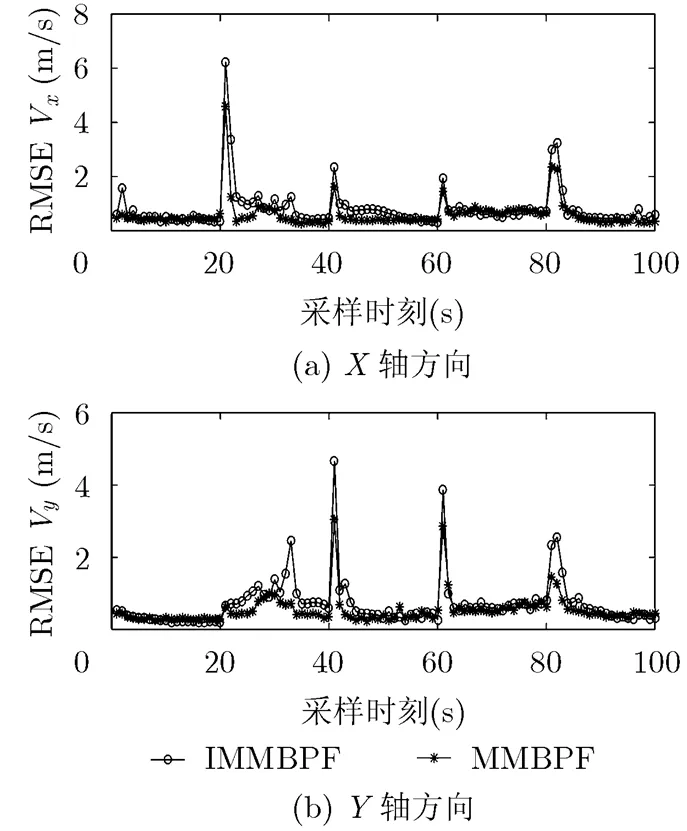
图3 速度RMSE曲线

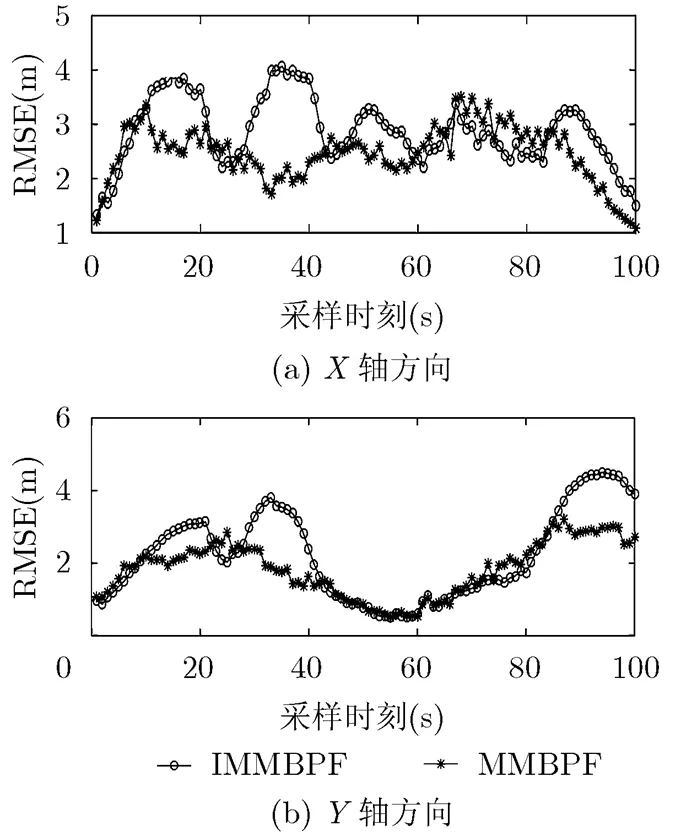
图4 位置RMSE曲线

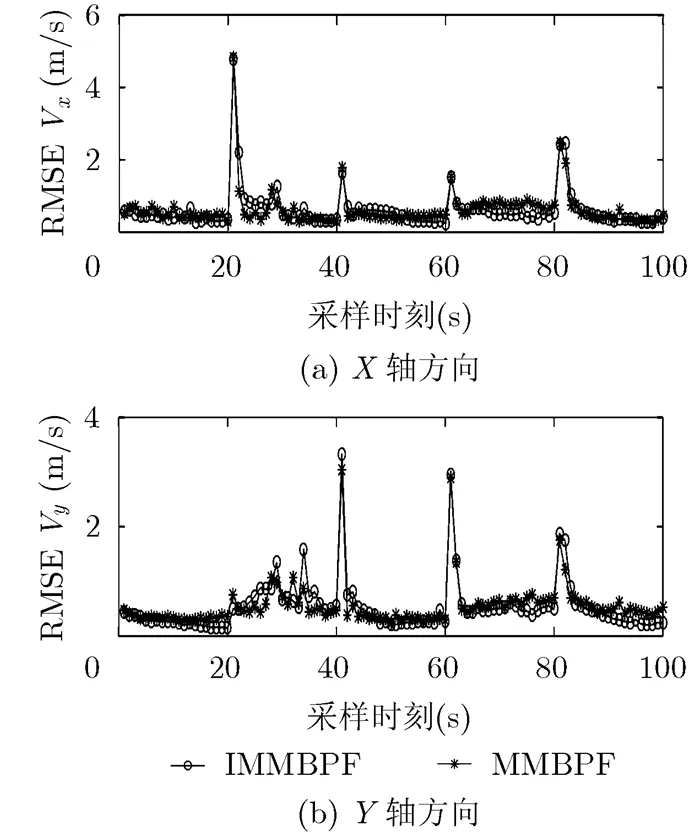
图5 速度RMSE曲线

[1] RISTIC B, VO B T, VO B N,. A tutorial on Bernoulli filters: Theory, implementation and applications[J]., 2013, 61(13): 3406-3430. doi: 10.1109/TSP.2013.2257765.

[2] VO B T, VO B N, HOSEINNEZHAD,. Robust multi-Bernoulli filtering [J].2013, 7(3): 399-409. doi: 10.1109/JSTSP.2013. 2252325.

[3] PAPI F, KYOVTOROV V, GIULIANNO R,. Bernoulli filter for track-before-detect using MIMO radar[J]., 2014, 21(9): 1145-1149. doi: 10.1109/LSP.2014.2325566.

[4] VO B T, SEE C M, MA N,. Multi-sensor joint detection and tracking with the Bernoulli filter[J]., 2012, 48(2): 1385-1402. doi: 10.1109/TAES.2012.6178069.

[5] GRAMSTROM K, WILLETT P, and BARSHALOM Y. A Bernoulli filter approach to detection and estimation of hidden Markov models using cluttered observation sequences[C]. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 2015: 3911-3915. doi: 10.1109/ICASSP.2015.7178704.

[6] BLOM H A P. An efficient filter for abruptly changing systems[C]. IEEE Proceedings of 23th Conference on Decision and Control, Las Vegas, NV, USA, 1984, Vol.23: 656-658. doi: 10.1109/CDC.1984.272089.

[7] MCGINNITY S and IRWIN G W. Multiple model bootstrap filter for maneuvering target tracking[J]., 2000, 36(3): 1006-1012. doi: 10.1109/7.869522.

[8] 刘贵喜, 高恩克, 范春宇. 改进的交互式多模型粒子滤波跟踪算法[J]. 电子与信息学报, 2007, 29(12): 2810-2813. LIU Guixi, GAO Enke, and FAN Chunyu. Tracking algorithms based on improved interacting multiple model particle filter[J].&, 2007, 29(12): 2810-2813.

[9] BOERS Y and DRIESSEN H. Interacting multiple model particle filter[J].-,, 2003, 150(5): 344-349. doi: 10.1049/ip-rsn: 20030741.

[10] DRIESSEN H and BOERS Y. Efficient particle filter for jump Markov nonlinear systems[J].-, 2005, 152(5): 323-326. doi:10.1049/ ip-rsn:20045075.

[11] YANG Wei, FU Yaowen, LONG Jianqian,. Random finite sets-based joint maneuvering target detection and tracking filter and its implementation[J]., 2012, 6(7): 648-660. doi: 10.1049/iet-spr. 2011.0171.

[12] DUNNE D and KIRUBARAJAN T. Multiple model multi-Bernoulli filters for maneuvering targets[J]., 2013, 49(4): 2679-2692. doi: 10.1109/TAES.2013.6621845.

[13] YANG Yanbo, ZOU Jie, YANG Feng,. An adaptive particle filter based on the mixing probability[C]. IEEE International Congress on Image and Signal Processing (CISP), Chongqing, China, 2012: 1480-1484. doi: 10.1109/ CSIP. 2012.6469724.

[14] 鉴福升, 徐跃民, 阴泽杰. 改进的多模型粒子滤波机动目标跟踪算法[J]. 控制理论与应用, 2010, 27(8): 1012-1016.

JIAN Fusheng, XU Yueming, and YIN Zejie. Enhanced multiple model particle filter for maneuvering target tracking[J].&, 2010, 27(8): 1012-1016.

Multiple Model Bernoulli Particle Filter for Maneuvering Target Tracking

YANG Feng ZHANG Wanying

(,,710129,)(,,710129,)

Interacting Multiple Model Bernoulli Particle Filter (IMMBPF) is suitable for maneuvering target tracking under cluttered environment. However, when model information is introduced into particle sampling process in IMMBPF, it will lead to the number decline of particles which are applied to approaching the real state and model, and the computation load is heavy because of the interacting stage of particles in the recursion. An enhanced Multiple Model Bernoulli Particle Filter (MMBPF) is proposed to improve the effectiveness of single particle to approximate the real target state and model. The number of particles of each model is given in advance, and the posterior probability of each model is updated with the associate likelihood function, which avoids particle degeneracy without distorting the Markov property. Simulation results show that the proposed MMBPF achieves better tracking performance with fewer particles than IMMBPF.

Maneuvering target tracking; Bernoulli filter; Particle filter; Multiple model

TP391

A

1009-5896(2017)03-0634-06

10.11999/JEIT160467

2016-05-09；改回日期：2016-11-28；

2017-01-11

张婉莹 zhangwanying0418@163.com

国家自然科学基金(61135001, 61374159, 61374023)，西北工业大学研究生创意创新种子基金(Z2016149)

The National Natural Science Foundation of China (61135001, 61374159, 61374023), Seed Foundation of Innovation and Creation of Graduate Students in Northwestern Polytechnical University (Z2016149)

杨 峰： 男，1977年生，副教授，主要研究方向为多源信息融合、目标跟踪等.

张婉莹： 女，1993年生，硕士生，研究方向为多源信息融合、目标跟踪等.