利用拟合优度检验的NPLSC-DSSS信号伪码盲估计

赵知劲 强芳芳 李 淼 沈 雷 王海泉



利用拟合优度检验的NPLSC-DSSS信号伪码盲估计

赵知劲 强芳芳*李 淼 沈 雷 王海泉

(杭州电子科技大学通信工程学院 杭州 310018)

针对非周期短码扩频长码加扰直扩(NPLSC-DSSS)信号的伪码估计问题，该文首先给出了m序列三阶相关函数(TCF)共同峰理论和NPLSC-DSSS信号TCF估计量的概率函数。其次，利用TCF峰的共轭系特性构建了TCF峰值序列，提出了TCF共同峰检测的二元假设模型和利用拟合优度检验的TCF共同峰精检测算法。同时，为提高伪码估计性能，该文利用正反向TCF三阶相关峰性质和共轭系TCF峰值点累加和递增性质排除大量伪峰。最后通过矩阵斜消法实现长短伪码的盲估计。仿真结果表明，该文方法在低信噪比条件下能够有效估计NPLSC-DSSS信号的伪随机码。

扩频通信；长短码直扩信号；三阶相关理论；拟合优度检验；伪码盲估计

1 引言

随着扩频通信的不断发展，短码扩频长码加扰的直扩(LSC-DSSS)信号应用越来越广泛。由于长伪码周期过长，接收端很难截获包含一个及以上的长伪码周期的信号，给伪码盲估计带来困难和挑战。

针对长码扩频的直扩信号扩频码盲估计，文献[1,2]提出宽窗口法解决特征分解法带来的酉模糊问题；文献[3]提出重叠分段特征分解法；文献[4]提出分段矩阵特征分解法和基于最优移位相加特性的信息码剥离算法估计周期长码直扩信号的扩频码；文献[5]对接收信号构成的观测矩阵进行奇异值分解，通过左奇异向量实现扩频码序列盲估计。

非周期短码扩频长码加扰直扩(NPLSC-DSSS)信号可利用的信号样本不足一个长码周期，不能采用以上方法。文献[6]提出三阶相关函数(TCF)理论，相比特征分解法，其对信息缺失不敏感。文献[10]提出了基于m序列共同峰的伪码估计方法，但此方法需要预先给定TCF峰值点集合。

本文在文献[10]提出的共同峰理论基础上，分析了NPLSC-DSSS信号TCF估计量的概率函数，提出了基于拟合优度检验的伪码盲估计方法，并利用正反向TCF峰值点性质以及共轭系TCF峰值点累加和递增性质排除大量伪峰，提高伪码估计性能。

2 理论基础

2.1 信号模型

假设已知NPLSC-DSSS信号的扩频码码片速率，以扩频码码片速率进行采样，并将信号映射为信号，则基带信号的采样值可表示为[11]

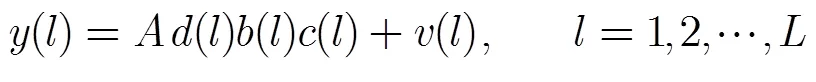
2.2 长短码的TCF共同峰

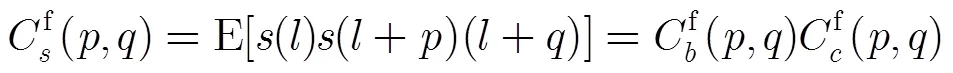
(3)

2.3 NPLSC-DSSS信号TCF估计量的概率函数

接收信号通过延迟相乘法消除信息码干扰：

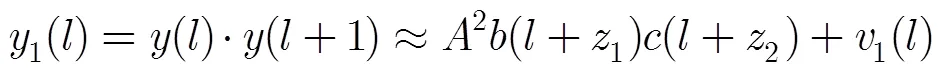
(6)

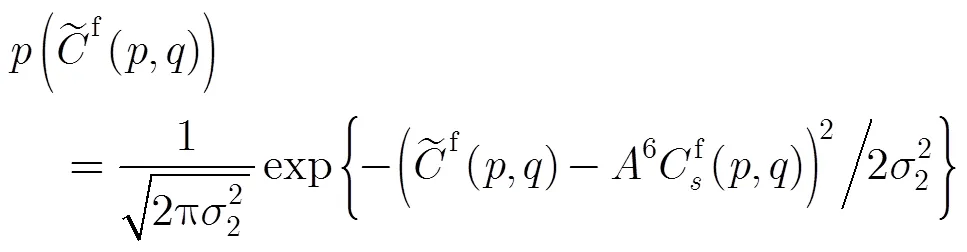
3　基于拟合优度的长短伪码盲估计

3.1 利用拟合优度检验的TCF共同峰检测

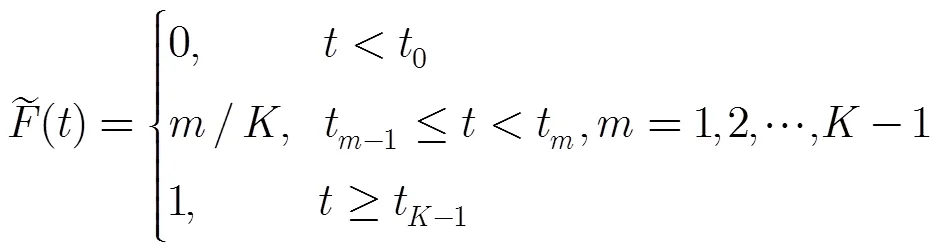
(11)

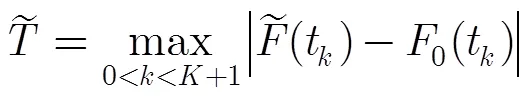
(13)

3.2 共同峰粗提取

为提高效率和伪码估计性能，在进行拟合优度检验前需排除大量虚假共同峰，实现共同峰粗提取。

性质3：共轭系TCF峰值点累加和呈递增趋势。

本文通过以上3个性质完成共同峰的粗提取。

3.3 长短伪码盲估计步骤

综上所述，基于拟合优度检验的NPLSC-DSSS信号的长短伪码盲估计算法步骤为：

(2)共同峰粗提取。由限幅、共同峰匹配及共轭系性质筛选可能共同峰，记入集合，完成粗提取。

(5)伪码盲估计。通过矩阵斜消法求最大公因式，因式分解可得长短伪码本原多项式，完成估计。

3.4 算法复杂度分析

本文所提算法的步骤(1)中信号正反向TCF的计算复杂度为；步骤(2)实现共同峰粗提取，复杂度为；步骤(3)中拟合优度KS检验的复杂度为；步骤(4)的复杂度为；步骤(5)中矩阵斜消的复杂度为，因式分解的复杂度为，其中为最大公因式的阶数。由于，故本文算法的复杂度为。

4 算法仿真与性能分析

4.1 TCF共同峰检测

由图1至图3可知，限幅提取得到大量伪峰，经过正反向TCF峰值点性质和共轭系性质可排除大量伪峰，再利用KS检验进一步筛选可能共同峰值点，大大提高了共同峰检测的正确率。

4.2 不同长码的NPLSC-DSSS信号伪码估计性能

短码选取同4.1节。长码选用3个周期不同的m序列，构成信号1，信号2和信号3，选择如表1所示。假设信息码已知，，则100次蒙特卡罗仿真估计得到的长短码序列本原多项式均正确的概率与信噪比的关系曲线如图4所示。

由图4可知，对于信号1，信号2和信号3，达90%以上正确估计概率所需的信噪比分别为-3.6 dB, -3.1 dB和0.4 dB。这是因为长码周期越短，相同长度的信号中其周期特性越明显，接收信号范围内存在的共同峰越多，因此伪码估计的正确率越高。

4.3 不同长度的NPLSC-DSSS信号伪码估计性能

扩频码和长扰码选取同4.1节。在信息码已知及未知情况下，当信号长度分别取,和时，仿真结果如图5和图6所示。

表1 信号1-信号3的长码m序列

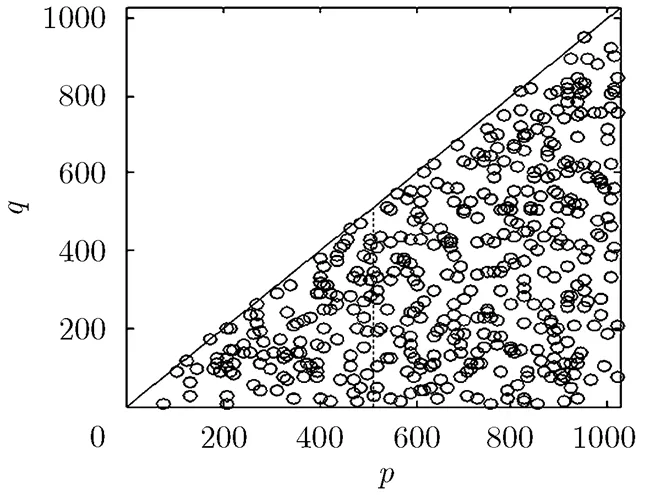
图1 限幅提取

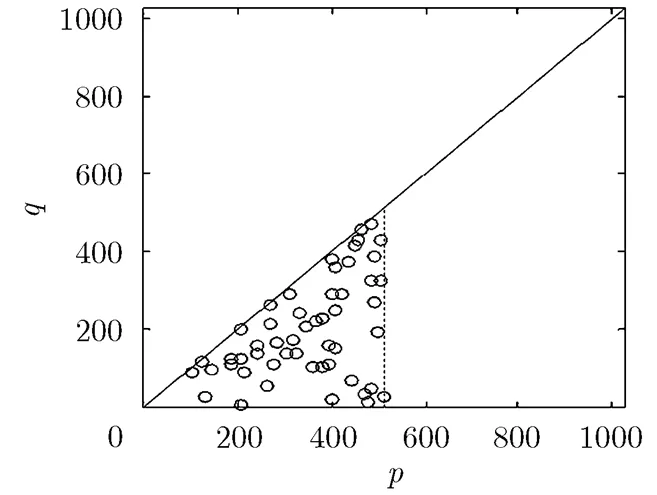
图2 共同峰粗提取

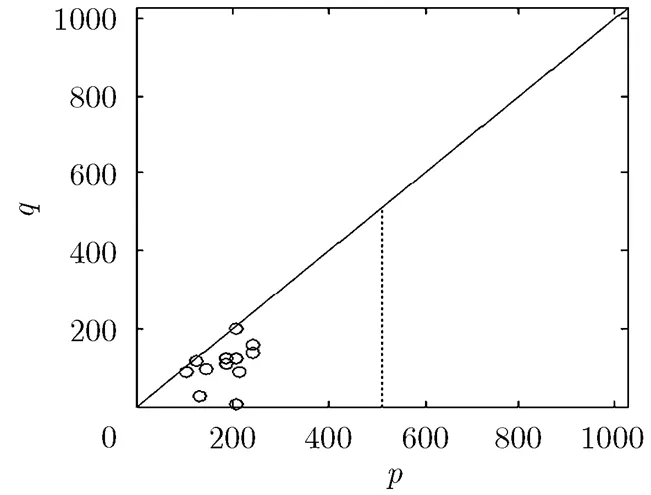
图3 拟合优度精检测

图4 长扰码对估计性能影响

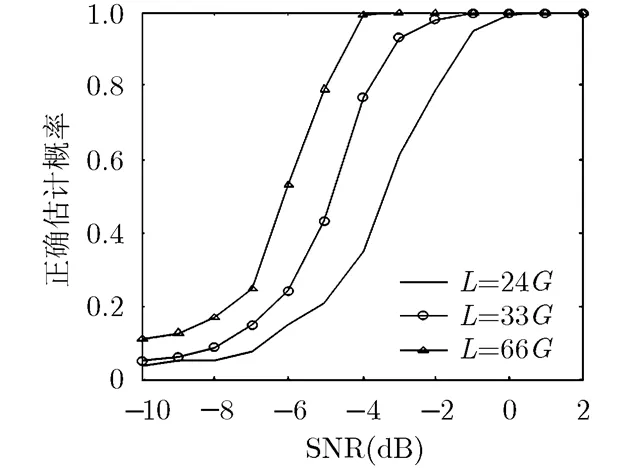
图5 信息码已知时估计性能

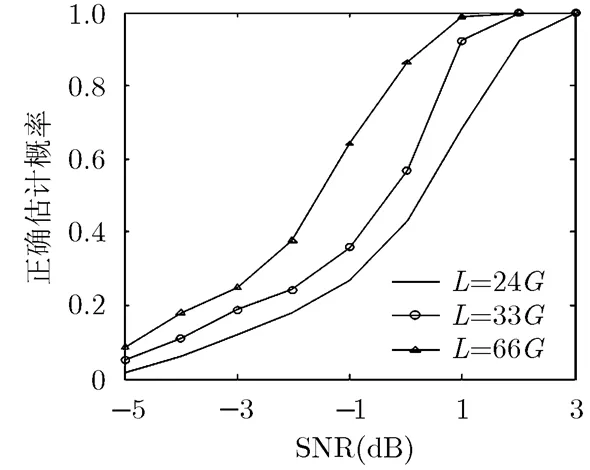
图6 信息码未知时估计性能

4.4 算法性能对比

为了能够进一步验证本文算法的性能，与文献[10]提出的算法进行比较。长短伪码本原多项式的选取与4.1节相同，接收信号长度分别为和，在信息码已知和未知两种情况下100次蒙特卡罗实验得到的仿真结果如图7和图8所示。

由图7和图8可知，本文算法性能优于文献[10]所提出的算法。当伪码正确估计概率为90%、信号长度分别为和，信息码已知时本文算法比文献[10]算法提高信噪比约为3.9 dB和2.3dB；信息码未知时，本文算法比文献[10]算法提高信噪比约为0.9 dB和0.5 dB。这是因为本文采用拟合优度检测方法，结合正反向TCF峰值点匹配法及共轭系求和法筛选可能共同峰，提高了共同峰检测的准确性。此外，本文检测峰值点的范围远小于文献[10]，故在提高估计性能的前提下也大大降低了运算量，提高了计算速度。

5 结束语

针对短码扩频、长码加扰的NPLSC-DSSS信号，本文构造了TCF峰值序列，提出了TCF共同峰检测的二元假设检验模型，结合正反向TCF峰值点和共轭系峰值点性质消除伪峰的干扰，提出了基于拟合优度检验的长短伪码盲估计方法。仿真结果表明了本文方法能够有效估计NPLSC-DSSS信号的长短伪码。

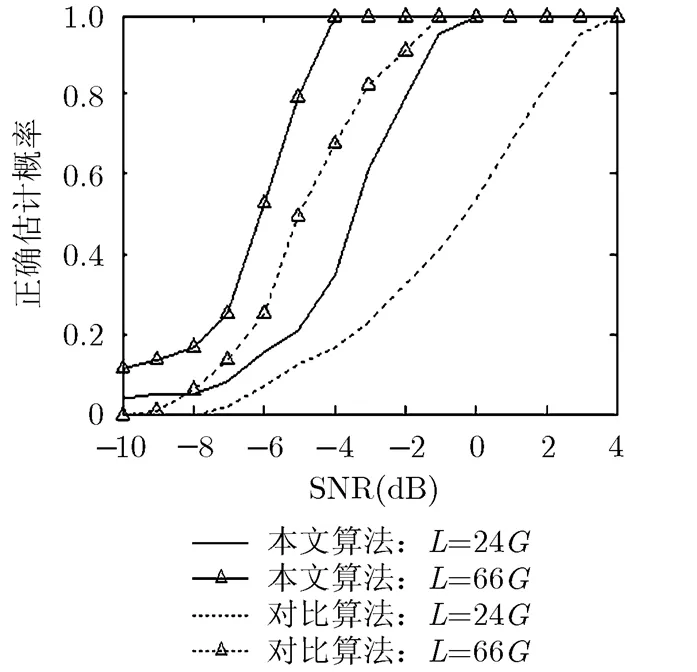
图7 信息码已知时算法对比

图8 信息码未知时算法对比

[1] ZHANG Tianqi and ZHANG Chao. An unsupervised adaptive method to eigenstructure analysis of lower SNR DS signals[J]., 2006, 89(6): 1943-1946. doi: 10.1093/ietcom/e89-b.6.1943.

[2] ZHANG Tianqi and MU Aiping. A modified eigen-structure analyzer to lower SNR DS-SS signals under narrow band interferences[J]., 2008, 18(4): 526-533. doi: 10.1016/j.dsp.2007.07.002.

[3] QIU P Y, HUANG Z T, JIANG W L,. Blind classification of the short-code and the long-code direct sequence spread spectrum signals[J]., 2010, 4(1): 78-88. doi: 10.1049/iet-spr.2009.0033.

[4] 王满喜, 李宏, 马刈非, 等. 低信噪比下非周期性直扩信号的盲估计[J]. 电子科技大学学报, 2009, 38(2): 177-181. doi: 10.3969/j.issn.1001-0548.2009.02.05.

WhANG Manxi, LI Hong, MA Yifei,. Blind estimation of lower SNR aperiodic DS signals[J]., 2009, 38(2): 177-181. doi: 10.3969/j.issn.1001-0548.2009.02.05.

[5] 沈斌, 王建新. 基于奇异值分解的直扩信号伪码序列及信息序列盲估计方法[J]. 电子与信息学报, 2014, 36(9): 2098-2103. doi: 10.3724/SP.J.1146.2013.01692.

SHEN Bin and WANG Jianxin. Blind estimation of the PN sequence and information sequence of a DSSS signal based on SVD[J].&, 2014, 36(9): 2098-2103. doi: 10.3724/SP.J.1146.2013.01692.

[6] WARNER E S, MULGREW B, and GRANT P M. Triple correlation analysis of m-sequences[J]., 1993, 29(20): 1755-1756. doi: 10.1049/el:19931169.

[7] 沈斌, 王建新. 窄带干扰条件下含有未知载频的直扩信号的伪码序列估计[J]. 电子与信息学报, 2015, 37(7): 1556-1561. doi: 10.11999/JEIT141322.

SHEN Bin and WANG Jianxin. Estimation of PN sequence in DSSS signals with unknown carrier frequency under narrow band interferences[J].&, 2015, 37(7): 1556-1561. doi: 10.11999/ JEIT141322.

[8] 赵知劲, 李淼, 詹毅. LSC-DSSS信号长短伪码盲估计[J]. 信号处理, 2016, 32(3): 268-275. doi: 10.16798 /j.issn.1003-0530. 2016.03.003.

ZHAO Zhijin, LI Miao, and ZHAN Yi. Blind estimation of long and short PN code in LSC-DSSS signals[J]., 2016, 32(3): 268-275. doi: 10.16798/j.issn. 1003-0530.2016.03.003.

[9] 赵知劲, 顾骁炜, 沈雷. 非周期长码直扩信号的长扰码识别[J]. 电子与信息学报, 2014, 36(8): 1792-1797. doi: 10.3724/SP.J. 1146.2013.01454.

ZHAO Zhijin, GU Xiaowei, and SHEN Lei. An identification method of long pseudo-random code sequence in non-periodic direct sequence spread spectral signals[J].&2014, 36(8): 1792-1797. doi: 10.3724/SP.J.1146.2013.01454.

[10] 赵知劲, 顾骁炜, 沈雷, 等. 非周期长码直扩信号的伪随机码盲估计[J]. 通信学报, 2015, 36(5): 27-34. doi: 10.11959/j.issn. 1000-436x.2015121.

ZHAO Zhijin, GU Xiaowei, SHEN Lei,. Blind estimation of pseudo-random codes in non-periodic long code direct- sequence spread-spectrum signals[J]., 2015, 36(5): 27-34. doi: 10.11959/j.issn. 1000-436x.2015121.

[11] FUSCO T, IZZO L, NAPOLITANO A,. On the second- order cyclostationarity properties of long-code DS-SS signals [J]., 2006, 54(10): 1741-1746. doi: 10.1109/TCOMM.2006.881353.

[12] 卢光跃, 叶迎晖, 孙宇, 等. 克服噪声不确定度的拟合优度检验频谱感知算法[J]. 电讯技术, 2016, 56(1): 26-31. doi: 10.3969/j.issn.1001-893x.2016.01.005.

LU Guangyue, YE Yinghui, SUN Yu,. A novel anti- noise-uncertainty spectrum sensing method using goodness of fit test[J]., 2016, 56(1): 26-31. doi: 10.3969/j.issn.1001-893x.2016.01.005.

[13] LUO Jinjun, WANG Shilian, ZHANG Eryang,. Non- cooperative signal detection in alpha stable noise via Kolmogorov-Smirnov test[C]. International Congress on Image and Signal Processing (CISP), Shenyang, 2015: 1464-1468.

[14] WANG Fanggang and WANG Xiaodong. Fast and robust modulation classification via Kolmogorov-Smirnov test[J]., 2010, 58(8): 2324-2332. doi: 10.1109/TCOMM.2010.08.090481.

[15] ASHWIN Lall. Data streaming algorithms for the Kolmogorov-Smirnov test[C]. IEEE International Conference on Big Data, Santa Clara, CA, USA, 2015: 95-104.

[16] Conover W J. 实用非参数统计[M]. 北京: 人民邮电出版社, 2006: 318-320.

Conover W J. Practical Nonparametric Statistics[M]. Beijing:Posts & Telecom Press, 2006: 318-320.

[17] 廖辉荣, 李国林, 李涛. 基于三阶相关的伪码调相脉冲信号周期预估计[J]. 航天电子对抗, 2011, 27(3): 39-42. doi: 10.3969/ j.issn.1673-2421.2011.03.013.

LIAO Huirong, LI Guoling, and LI Tao. Period estimation of phase-modulated pulse signal with PN code based on third-order correlation[J].2011, 27(3): 39-42. doi: 10.3969/j.issn.1673-2421.2011.03.013.

Blind Estimation of Pseudo-random Noise Codes in NPLSC-DSSS Signals Based on Goodness of Fit Test

ZHAO Zhijin QIANG Fangfang LI Miao SHEN Lei WANG Haiquan

(,,310018,)

For blind estimation of Pseudo-random Noise (PN) codes in Non-Periodic Long and Short Codes Direct Sequence Spread Spectrum (NPLSC-DSSS) signals, the Triple Correlation Function (TCF) common peak theory of m-sequence and probability function of NPLSC-DSSS signals’ TCF estimate are given firstly. Then sequences of TCF peaks are built with their conjugate sets’ features, binary hypothesis test model and accurate detection algorithm of TCF common peaks using goodness of fit test are proposed. Meanwhile, many false peaks are eliminated to improve the estimation performance using the property of forward and backward TCF peaks and cumulative-sum’s increasing trend of TCF peaks in conjugate sets. Lastly, the primitive polynomials of long and short pseudo-random codes can be estimated with the matrix’s oblique elementary method. Simulations show that the proposed method can effectively estimate the PN codes of NPLSC-DSSS signal at low Signal-to-Noise Ratio (SNR).

Spread spectrum communication; Long and Short Codes Direct Sequence Spread Spectrum (LSC- DSSS); Triple correlation theory; Goodness of fit test; Pseudo-random Noise (PN) codes blind estimation

TN914.42

A

1009-5896(2017)03-0749-05

10.11999/JEIT160541

2016-05-06；改回日期：2016-10-31；

2016-12-20

强芳芳 qiangffmy@163.com

国家自然科学基金(61571172)

The National Natural Science Foundation of China (61571172)

赵知劲： 女，1959年生，教授，博士生导师，研究方向为信号处理、软件无线电技术.

强芳芳： 女，1992年生，硕士生，研究方向为信号处理.

李 淼： 女，1990年生，硕士生，研究方向为软件无线电.

沈 雷： 男，1979年生，副教授，硕士生导师，研究方向为信号检测、信号盲分离.

王海泉： 男，1964年生，教授，硕士生导师，研究方向为信号检测和MIMO通信.