基于平行嵌套阵互协方差的二维波达角联合估计算法

李建峰 蒋德富 沈明威



基于平行嵌套阵互协方差的二维波达角联合估计算法

李建峰*蒋德富 沈明威

(河海大学计算机与信息学院 南京 211100)

论文提出基于平行嵌套阵互协方差的2维(Two Dimensional, 2D)波达角(Direction Of Arrival, DOA)联合估计算法。算法基于两个互相平行的嵌套阵的互协方差生成较长虚拟阵列，同时将2维DOA估计问题降维为1维 DOA估计问题。在构造协方差矩阵时，利用方向矩阵范德蒙特性增加虚拟快拍数，保证了孔径的最小损失。最后算法基于酉旋转不变技术(Estimation of Signal Parameters via Rotational Invariance Technique, ESPRIT)和总体最小二乘(Total Least Squares, TLS)方法进一步降低噪声影响，并获得了自动配对的2维DOA估计。相比传统平行阵下的DOA估计算法，该算法拥有更好的DOA估计性能，能辨识更多的空间信源，对空间色噪声有更强的鲁棒性。仿真结果验证了算法的有效性。

2维DOA估计；酉ESPRIT；平行嵌套阵；互协方差

1 引言

波达角(Direction Of Arrival, DOA)估计是阵列信号处理中的重要问题，其在无线通信、声呐以及雷达等系统均有广泛应用。为了克服1维(One Dimensional, 1D) DOA估计在处理实际空间信源时的局限，2D DOA估计近年来受到较多关注和研究，许多阵列如L型阵列[5]，面阵[6]等被用来进行有效的2D参数估计。文献[7]中提出的双平行阵能以较少的阵元和较低的复杂度获得信号源的2D DOA估计，并可有效解决2维DOA估计中的角度配对问题，但文献[7]中提出的DOA矩阵法孔径利用率较低。之后文献[8]提出了基于该双平行阵的多重信号分类(MUltiple SIgnal Classification, MUSIC)方法，进一步提高了孔径利用率。文献[9]则将传播算子方法(Propagator Method, PM)应用于双平行阵，并结合借助旋转不变技术的参数估计(Estimation of Signal Parameters via Rotational Invariance Technique, ESPRIT)思想，降低了2D DOA估计的复杂度。文献[10]则研究了存在非圆信号时的2维DOA估计问题，而文献[11]则利用多个平行阵来增加可用信息获得方位角的有效估计。然而这些算法均是基于传统紧凑型的均匀阵列，难以获得较大的自由度(Degrees Of Freedom, DOF)，辨识信号个数有限。

稀疏阵以其能产生较大的有效DOF而被广泛关注[12]，如最小冗余阵(Minimum Redundancy Array, MRA)[13,14]，互质阵(Co-Prime Array, CPA)[15]以及嵌套阵等。嵌套阵可利用个物理阵元产生O(2)的DOF[16]，且可产生较多连续虚拟阵元，避免DOA估计模糊问题，但目前基于嵌套阵的研究大都基于1D DOA，没有考虑2D情况，以及其带来的复杂度、配对等问题。

本文将双平行阵与嵌套阵相结合，提出了基于平行嵌套阵互协方差(Cross Covariance Matrix, CCM)的2D DOA估计算法。通过互相平行的两个子阵间的互协方差降低噪声影响，充分利用嵌套阵特性生成虚拟阵列，将2D DOA估计问题降维为1D DOA估计问题。利用虚拟快拍数构造协方差矩阵，保证有效孔径。最后基于酉ESPRIT方法和总体最小二乘(Total Least Squares, TLS)获得自动配对的2D DOA估计的闭式解。该算法在DOA估计性能、可辨识信源数以及对色噪声鲁棒性方面，均优于文献[7]中的DOA矩阵法、文献[8]中的求根MUSIC方法以及文献[9]中的改进PM方法。

本文安排如下：第2节介绍了平行嵌套阵进行2D DOA估计的阵列结构和数据模型；第3节则详细阐述了基于平行嵌套阵CCM的2维DOA估计算法；第4节则是算法总结和复杂度分析对比；第5节为实验仿真结果，而第6节是总结。

2 数据模型

不同于传统双平行均匀线阵(Uniform Linear Array, ULA)，为了增加DOF，本文采用如图1所示的平行嵌套阵来进行空间信号2维DOA估计。元的子阵1为紧凑型ULA，位于轴，其阵元间距为半波长()，同样为元的子阵2为稀疏ULA，平行于子阵1，其阵元间距为，子阵1和子阵2之间间距为半波长，具体阵列结构见图1。假设空间存在个远场窄带信号入射到该阵列上，和为第个信号源的仰角和方位角。为方便起见，根据文献[8]，这里采用信号与轴和轴的交角(和)作为信号的2维DOA，它们与传统仰角和方位角的关系为和。那么两个子阵的输出分别为

] (2)

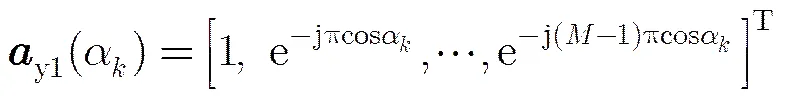
(4)

3 基于平行嵌套阵CCM的2D DOA估计算法

3.1 虚拟阵列生成

将子阵1的输出进行逆向排序：

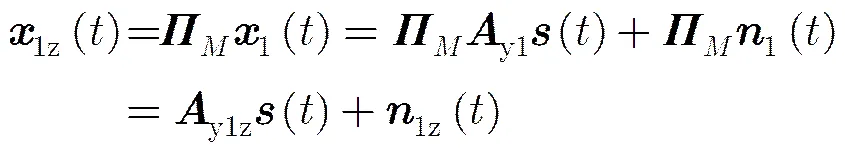
逆向排序后的子阵1输出和子阵2输出之间的CCM为

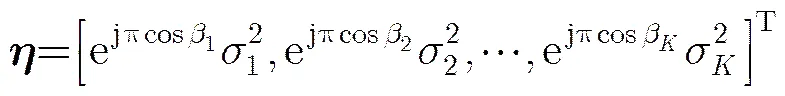
将互协方差矩阵按列拉伸为一长矢量：

(7)

另外，实际中只能通过有限快拍数求式(6)中的互协方差，即，其中为快拍数，所以依然会存在残余的噪声影响。为了进一步降低噪声的影响，根据文献[16]，需要使构造的数据矩阵的虚拟快拍数大于等于虚拟阵元数，从而能增强协方差的秩，有效将噪声能量分配到噪声子空间。

3.2 协方差矩阵构造

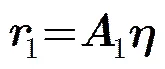
(10)

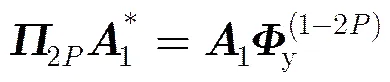
因此定义增广矩阵为

(13)

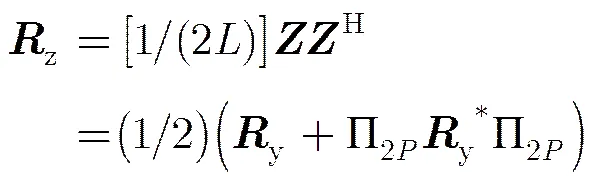
(15)

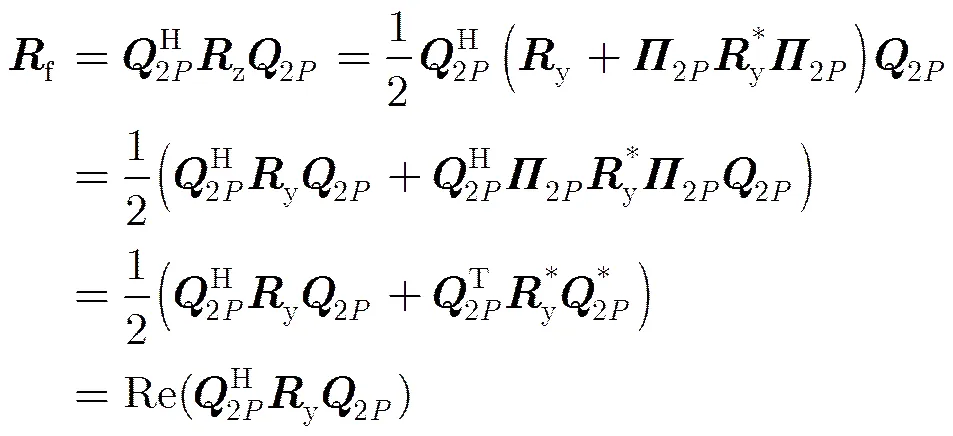
此时协方差矩阵变为实数矩阵，可降低之后特征分解的复杂度，且其可直接从构造获得，酉变换之后的方向矩阵由变为。

3.3 2维DOA估计

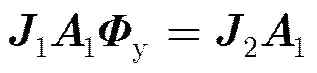
(18)

式(16)中得到的实数协方差进行特征分解之后，其最大的个特征值对应的特征矢量称为信号子空间，记为，其和方向矩阵之间满足，其中为一个×的非奇异矩阵。将代入式(18)，得到

(20)

令

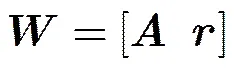
(22)

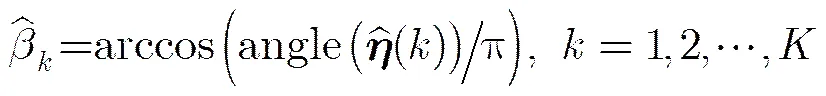
4 算法总结和分析

4.1 算法步骤总结

将基于平行嵌套阵CCM的2维DOA估计算法的步骤总结如下：

步骤1 将子阵1输出逆向排序，并求其与子阵2输出的CCM,；

4.2 算法优点总结

将基于平行嵌套阵CCM的2维DOA估计算法的优点总结如下：

(1)基于CCM生成较长虚拟阵列，可处理更多信源；

(2)将2D DOA转变为1D DOA估计问题，并基于酉变换增加虚拟快拍，保证有效孔径的同时降低复杂度；

(3)CCM对空间色噪声有较强的鲁棒性；

4.3 复杂度分析

所提算法运算的主要运算复杂度包括求协方差、特征分解、LS以及TLS等，涉及到的复乘次数共约O(2+22(2++4)+42+3)次。基于同样阵元数的平行阵，文献[7]中的DOA矩阵法需要复乘次数约O(22+43+2)次，文献[8]中的求根MUSIC方法需要复乘次数约O(42+ 83+2+4)次，以及文献[9]中的改进PM方法需要复乘次数约O(42+42+42+3)次。所提算法无需谱峰搜索以及迭代等，计算复杂度跟DOA矩阵法、求根MUSIC方法以及改进PM方法处于同一级别。

4.4 最大可辨识信源数分析

根据式(13)，算法最终采用的虚拟数据长度为2，结合后期采用的ESPRIT方法进行子阵选择，可知算法最大可辨识信源数为，即，这一般已经大于实际物理阵元数2。DOA矩阵法[7]和改进PM方法[9]可辨识个信源，而文献[8]中的求根MUSIC可辨识2(-1)个信源，均小于所提算法的可辨识信源数。在下一节，我们将通过一些仿真验证这一结果。

5 仿真结果

采用求根均方误差(Root Mean Square Error, RMSE)衡量算法DOA估计性能，其定义为

图2给出了所提算法在所有500次仿真下2维DOA估计的散布图，实心点代表估计值，十字符号代表真实DOA值。从图中可以知道，算法可有效地估计出信源的2维DOA，且2维DOA自动配对。

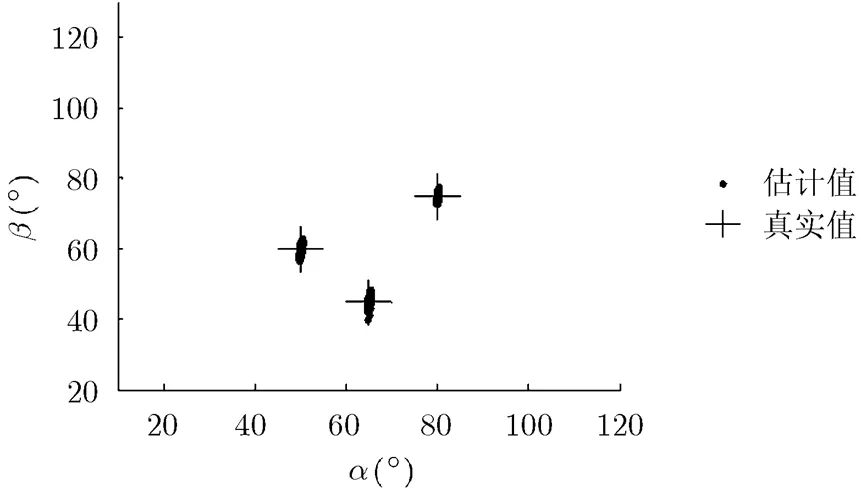
图2 所提算法2维DOA估计结果(N=500次仿真，SNR=9 dB)

图3则是所提算法与文献[7]中的DOA矩阵法、文献[8]中的求根MUSIC方法以及文献[9]中的改进PM方法的DOA估计性能对比，在RMSE的衡量下，可以发现所提算法的角度估计性能优于其余算法，尤其是在低信噪比(Signal to Noise Ratio, SNR)下。主要原因是所提算法利用嵌套阵特性扩展了DOF，同时利用互协方差降低了噪声影响，因此可获得较好的估计性能。

图4和图5给出了信源数较大的情况下，算法的估计结果。图4中，因为=4，而此时=6，已经大于了DOA矩阵法和改进PM方法的最大处理信源数，所以它们此时均已失效，而=6也是求根MUSIC方法的最大可处理信源数，在一定的噪声下，此时其估计结果也存在较大误差。而根据以上分析，所提算法最大可辨识信源数为，所以所提算法依然可以正常工作。在图5中给出了=9时所提算法的估计结果，可以发现算法能准确辨识出所有信源的2维DOA。

图6给出了当噪声不再是白噪声，而是文献[20]中采用的空间色噪声时(噪声能量随机分布)，各算法的估计性能。可以发现，此时在其余算法性能出现下降的时候，所提算法依然保持了有效的DOA估计性能，从而验证了第3.1节中所说的算法对空间色噪声的鲁棒性。

图3 算法2维DOA估计性能对比

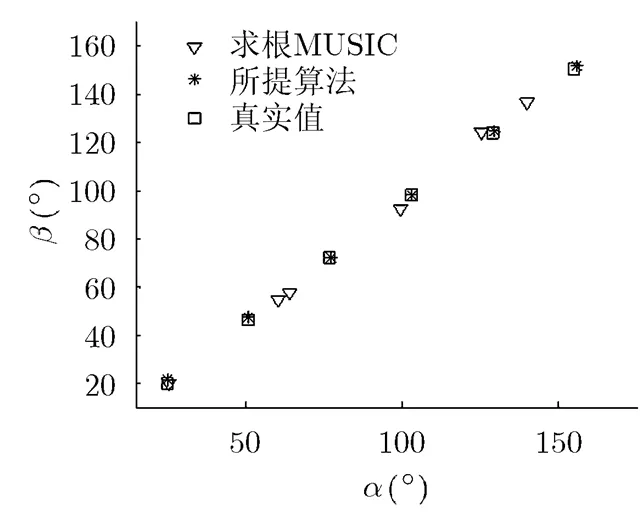
图4 K=6情况下，算法DOA估计结果对比(SNR=10 dB)

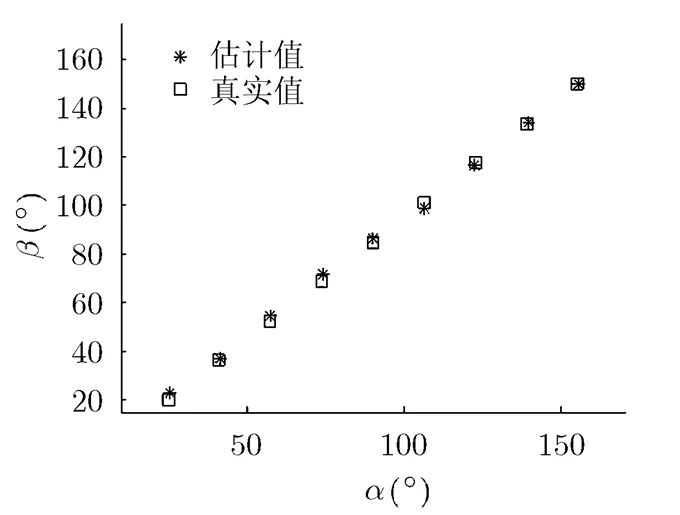
图5 K=9情况下，所提算法DOA估计结果 (SNR=10 dB)

图6 空间色噪声情形下算法2维DOA估计性能对比

6 结束语

本文将传统平行阵与嵌套阵相结合，提出了基于平行嵌套阵CCM的2D DOA估计算法。该算法可利用平行嵌套阵的CCM获得较大DOF，将2D DOA问题转变为1D DOA估计，最终结合酉ESPRIT和TLS方法获得自动配对的2D DOA估计的闭式解，复杂度较低。通过分析和仿真，该算法在DOA估计性能、可辨识信源数以及对色噪声鲁棒性方面，均优于传统方法。所提算法可应用于无线信号测向以及雷达目标定位等系统，但所提算法基于互协方差的矢量化来获得虚拟孔径，因此需要信号之间不相干，对于相干信号，则需要一些前期的解相干手段，这也是我们未来研究方向。

[1] Gershman A B, Rübsamen M, and Pesavento M. One-and two-dimensional direction-of-arrival estimation: An overview of search-free techniques [J]., 2010, 90(5): 1338-1349.doi: 10.1016/j.sigpro.2009.12.008.

[2] CHEN H, ZHU W P, and SWAMY M N S. Real-valued ESPRIT for two-dimensional DOA estimation of noncircular signals for acoustic vector sensor array[C]. IEEE International Symposium on Circuits and Systems (ISCAS), Lisbon, Portugal, 2015: 2153-2156. doi: 10.1109/ISCAS.2015. 7169106.

[3] 蔡晶晶, 鲍丹, 李鹏, 等. 强约束优化降维MUSIC二维DOA估计[J]. 电子与信息学报, 2014, 36(5): 1113-1118. doi: 10. 3724/SP.J.1146.2013.01127.

CAI Jingjing, BAO Dan, LI Peng,Two-dimensional DOA estimation using reduced-dimensional MUSIC algorithm with strong-constraint optimization[J].&, 2014, 36(5): 1113-1118. doi: 10.3724/SP.J.1146.2013.01127.

[4] 张小飞, 张立岑, 孙华普, 等. 双平行线阵中基于Euler变换传播算子的二维DOA估计算法[J]. 南京航空航天大学学报, 2015, 47(3): 324-331. doi: 10.16356/j.1005-2615.2015.03.002.

ZHANG Xiaofei, ZHANG Licen, SUN Huapu,Two-dimensional DOA estimation algorithm for two parallel linear arrays via Eular transformation and propagator method[J]., 2015, 47(3): 324-331. doi: 10.16356/j.1005-2615. 2015.03.002.

[5] GU J F, ZHU W P, and SWAMY M N S. Joint 2-D DOA estimation via sparse L-shaped array[J]., 2015, 63(5): 1171-1182. doi: 10.1109/ TSP.2015.2389762.

[6] ZHANG W, LIU W, WANG J,Computationally efficient 2-D DOA estimation for uniform rectangular arrays [J].&, 2014, 25(4): 847-857. doi: 10.1007/s11045-013-0267-y.

[7] Yin Q Y, Newcomb R W, and Zou L H. Estimating 2-D angles of arrival via two parallel linear arrays[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing, Glasgow, UK, 1989: 2803-2806. doi: 10.1109/ ICASSP.1989.267051.

[8] Xia T, Zheng Y, Wan Q,Decoupled estimation of 2-D angles of arrival using two parallel uniform linear arrays [J]., 2007, 55(9): 2627-2632. doi: 10.1109/TAP.2007.904143.

[9] Li J, Zhang X, and Chen H. Improved two-dimensional DOA estimation algorithm for two-parallel uniform linear arrays using propagator method[J]., 2012, 92(12): 3032-3038. doi: 10.1016/j.sigpro.2012.06.010.

[10] CHEN H, HOU C, LIU W,Efficient two-dimensional direction-of-arrival estimation for a mixture of circular and noncircular sources[J]., 2016, 16(8): 1-9. doi:10.1109/JSEN.2016.2517128.

[11] YANG L, LIU S, LI D,Fast 2D DOA estimation algorithm by an array manifold matching method with parallel linear arrays[J]., 2016, 16(3): 274-289. doi: 10.3390/s16030274.

[12] 崔琛, 梁浩, 余剑. 稀疏阵列MIMO雷达高精度收发角度联合估计[J]. 应用科学学报, 2015, 33(5): 527-540. doi: 10.3969/ j.issn.0255-8297.2015.05.007.

CUI Chen, LIANG Hao, and YU Jian. Joint DOD and DOA estimation with high accuracy in bistatic MIMO radar using sparse array[J]., 2015, 33(5): 527-540. doi: 10.3969/j.issn.0255-8297.2015.05.007.

[13] Moffet A. Minimum-redundancy linear arrays[J]., 1968, 16(2): 172-175. doi: 10.1109/TAP.1968.1139138.

[14] HU N, YE Z, XU X,DOA estimation for sparse array via sparse signal reconstruction[J]., 2013, 49(2): 760-773. doi: 10.1109/TAES.2013.6494379.

[15] Vaidyanathan P P and Pal P. Sparse sensing with co-prime samplers and arrays[J]., 2011, 59(2): 573-586. doi: 10.1109/TSP. 2010.2089682.

[16] Pal P and Vaidyanathan P P. Nested arrays: a novel approach to array processing with enhanced degrees of freedom[J]., 2010, 58(8): 4167-4181. doi: 10.1109/TSP.2010.2049264.

[17] 杨杰, 廖桂生. 基于空域稀疏性的嵌套MIMO雷达DOA估计算法[J]. 电子与信息学报, 2014, 36(11): 2698-2704. doi: 10. 3724/SP.J.1146.2013.01900.

YANG Jie and LIAO Guisheng. A spatial sparsity-based DOA estimation method in nested MIMO radar[J].&, 2014, 36(11): 2698-2704. doi: 10.3724/SP.J.1146.2013.01900.

[18] WU N and LIANG Q. Underwater DOA estimation based on nested array[C]. IEEE Military Communications Conference, Tampa, FL, USA, 2015: 216-221. doi: 10.1109/ MILCOM. 2015.7357445.

[19] 丁姗姗, 张永顺, 牛超, 等. 一种基于Khatri—Rao子空间的非均匀稀疏阵列[J]. 空军工程大学学报:自然科学版, 2015, 16(5): 78-82. doi: 10.3969/j.issn.1009-3516.2015.05.019.

DING Shanshan, ZHANG Yongshun, NIU Chao,A novel spare linear array geometry via Khatri_Rao subspace [J].(), 2015, 16(5): 78-82. doi: 10.3969/j.issn. 1009-3516.2015.05.019.

[20] 陈建锋, 吴云韬, 张贤达. 色噪声环境下的快速DOA估计算法[J]. 西安电子科技大学学报:自然科学版, 2004, 30(2): 151-154. doi: 10.3969/j.issn.1001-2400.2003.02.003.

CHEN Jianfeng, WU Yuntao, and ZHANG Xianda. A novel method for estimating DOA in the presnece of unknown colored noise fields[J].(), 2004, 30(2): 151-154. doi: 10.3969/j.issn. 1001-2400.2003.02.003.

[21] LI J and ZHANG X. Unitary subspace-based method for angle estimation in bistatic MIMO radar[J].,, 2014, 33(2): 501-513. doi: 10.1007/s00034-013-9653-9.

[22] Steinwandt J, Roemer F, and HAARDT M. ESPRIT-Type algorithms for a received mixture of circular and strictly non-circular signals[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing, South Brisbane, QLD, Australia, 2015: 2809-2813.doi: 10.1109/ICASSP.2015.7178483.

Joint Two-dimensional Direction of Arrival Estimation Based on Cross Covariance Matrix of Parallel Nested Array

LI Jianfeng JIANG Defu SHEN Mingwei

(,,211100,)

A Cross Covariance Matrix (CCM) based Two Dimensional (2D) Direction Of Arrival (DOA) estimation algorithm for parallel nested array is proposed. A long virtual array can be achieved based on the CCM between the two parallel nested arrays, and 2D DOA estimation can be transformed to a 1D DOA estimation problem. Thereafter, virtual snapshots are increased by exploiting the Vandermonde structure of direction matrix, and the aperture loss is minimized when constructing covariance matrix from the virtual array. Finally, the proposed algorithm employs unitary Estimation of Signal Parameters via Rotational Invariance Technique (ESPRIT) and Total Least Squares (TLS) to reduce further the influence of noise and achieve automatically paired 2D DOA estimation. Compared to DOA estimation algorithms using conventional parallel array, the proposed algorithm can achieve better DOA estimation performance, identify more signals and is more robust to spatial color noise. The simulation results verify the effectiveness of the proposed algorithm.

Two dimensional DOA estimation; Unitary ESPRIT; Parallel nested array; Cross covariance matrix

TN911.7

A

1009-5896(2017)03-0670-07

10.11999/JEIT160488

2016-05-12；改回日期：2016-09-06；

2016-11-17

李建峰 lijianfengtin@126.com

中央高校基本科研业务费专项资金(2015B12614)，江苏高校优势学科建设工程

The Fundamental Research Funds for the Central Universities (2015B12614), A Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions

李建峰： 男，1988年生，讲师，研究方向为阵列信号处理、雷达信号处理.

蒋德富： 男，1963年生，教授，研究方向为阵列信号处理技术、雷达通信集成系统的跟踪制导及目标识别技术.

沈明威： 男，1981年生，副教授，研究方向为自适应阵列技术、雷达信号处理.