有限链环上一类常循环码的距离

袁 健 朱士信 开晓山



有限链环上一类常循环码的距离

袁 健 朱士信*开晓山

(合肥工业大学数学学院 合肥 230009) (东南大学移动通信国家重点实验室 南京 210096)

在编码理论中，线性码的(最小)距离是一个极其重要的参数，它决定了码的纠错能力。设为任一有限交换链环，为其最大理想的一个生成元，为的乘法单位群。对于任意，该文利用上任意长度的-常循环码的生成结构，通过计算这类码的高阶挠码，得到了上任意长度的-常循环码的汉明距离，并研究了这类常循环码的齐次距离。这给编译有限链环上此类常循环码提供了重要的理论依据。

常循环码；有限链环；汉明距离；齐次距离

1 引言

自20世纪九十年代中期，Hammons等人[1]发现一些高效的二元非线性码为上线性码的Gray像以来，有限链环上纠错码一直是编码理论研究的热点。有限链环上的常循环码是一类非常重要的线性码。有限域或环上码的汉明距离在衡量码的纠错能力起重要作用，Norton和Sǎlǎgean[8]利用挠码研究有限链环上线性码的汉明距离。齐次距离在研究有限链环上码中非常重要[6,9]。在本文中，设为任一有限交换链环，为其最大理想的一个生成元，为的乘法单位群。对于任意，我们先引用关于上任意长度的-常循环码结构[10]。利用此生成结构性质，通过计算高阶挠码，结合代数计算程序MAGAM，得到了上任意长度的所有-常循环码的汉明距离，还研究并得到了这类码齐次距离的一些重要结果。

2 有限链环和常循环码

如果一个有限含幺交换环是局部环并且其最大理想是主理想，那么该环是有限链环。本文中以表示任一有限链环，表示的乘法单位群。设为的最大理想的一个生成元。于是为一幂零元，本文记为其幂零指数。本文记模其最大理想的剩余域为，即，其中为含有个元素的有限域，为的特征。的势为。到存在一个自然环满同态映射。此映射可以自然开拓为到的一个环同态，我们仍将它记作。对于任意，我们记其在下的像为。根据文献[11]，对于中任一非零元，存在唯一的和唯一的单位，使得，其中在模下唯一。对于，若有使得，则称在上互素。在上互素当且仅当在上互素[11]。

定理1[10]每一个互不相同的上长度为的-常循环码可唯一表示成，其中,。上长度为的-常循环码的数目为。上述码中码字数目为。

3 汉明距离和齐次距离

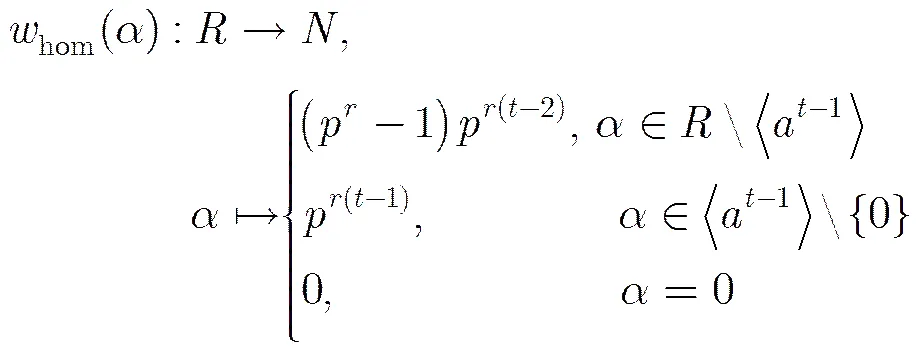
码中任一码字的齐次重量为它的所有分量的齐次重量的和。线性码的齐次距离为码所有非零码字的齐次重量中的最小值。汉明重量和汉明距离按照通常的定义。下面来研究上长度为的-常循环码的汉明距离和齐次距离。

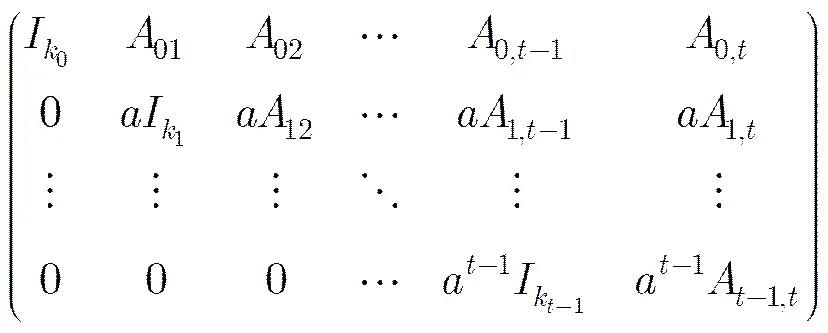
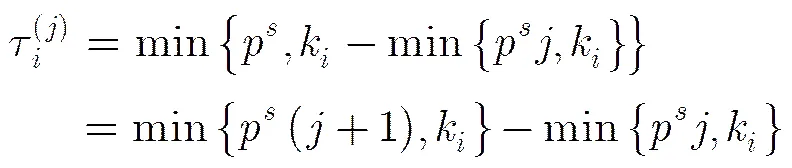
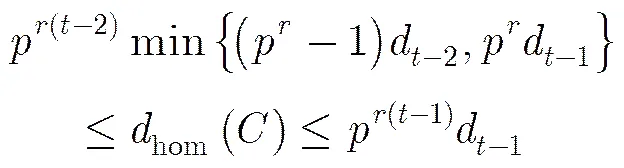
4 结束语

本文研究了有限链环上的一类常循环码的距离。根据这类常循环码的已知结构，通过计算其高阶挠码，对任一给定的这类常循环码，其汉明距离都可以利用本文方法计算。本文还探究了这类常循环码的齐次距离，得到了关于这类码的齐次距离的一个界，并得到了在某些特殊情况下这类码的精确的齐次距离。这给编译有限链环上此类常循环码提供了重要的理论依据。完全确定该类码在任意情况下的精确齐次距离是一个待研究的问题。

[1] HAMMONS A R Jr., KUMAR P V, CALDERBANK A R,. The-linearity of Kerdock, Preparata, Goethals and related codes[J]., 1994, 40(2): 301-319. doi: 10.1109/18.312154.

SHI M J, YANG S L, and ZHU S X. The distributions of distances of-constacyclic codes of lengthover[J].&, 2010, 32(1): 112-116. doi: 10.3724/ SP.J.1146.2008.01810.

[3] KONG B, ZHENG X Y, and MA H J. The depth spectrums of constacyclic codes over finite chain rings[J]., 2015, 338(2): 256-261. doi: 10.1016/j.disc.2014. 09.013.

[4] QIAN K Y, ZHU S X, and KAI X S. On cyclic self-orthogonal codes over[J]., 2015, 33: 53-65. doi: 10.1016/j.ffa.2014.11.005.

[5] DINH H Q, DHOMPONGSA S, and SRIBOONCHITTA S. Repeated-root constacyclic codes of prime power length overand their duals[J]., 2016, 339(6): 1706-1715. doi: 10.1016/j.disc.2016.01.020.

[6] WOLFMANN J. Negacyclic and cyclic codes over[J]., 1999, 45(7): 2527-2532. doi: 10.1109/18.796397.

[9] GREFERATH M and SCHMIDT S E. Gray isometries for finite chain rings and a nonlinear ternarycode[J]., 1999, 45(7): 2522-2524. doi: 10.1109/18.796395.

[10] CAO Y L. On constacyclic codes over finite chain rings[J]., 2013, 24: 124-135. doi: 10.1016/j.ffa.2013.07.001.

[11] MCDONALD B R. Finite Rings with Identity[M]. New York, Marcel Dekker Press, 1974: 56-97.

[12] DINH H Q. Constacyclic codes of lengthover[J]., 2010, 324(5): 940-950. doi: 10.1016/j.jalgebra.2010.05.027.

On Distances of Family of Constacyclic Codes over Finite Chain Rings

YUAN Jian ZHU Shixin KAI Xiaoshan

(,,230009,)(,,210096,)

In coding theory, the (minimum) distance of a code is a very important invariant, which always determines the error-correcting capability of the code. Letbe an arbitrary commutative finite chain ring,is a generator of the unique maximal ideal andis the multiplicative group of units of. In this paper, for any, by using the generator polynomials of-constacyclic codes of any length over, higher torsion codes of such codes are calculated. The Hamming distance of all-constacyclic codes of any length overis determined and the exact homogeneous distance of some such codes is obtained. The result provides a theoretical basis for encoding and decoding for such constacyclic codes.

Constacyclic codes; Finite chain rings; Hamming distance; Homogeneous distance

TN911.22

A

1009-5896(2017)03-0754-04

10.11999/JEIT160392

2016-04-22；改回日期：2016-09-23；

2016-11-14

朱士信 zhushixin@hfut.edu.cn

国家自然科学基金(61370089, 60973125)，东南大学国家移动通信研究实验室开放研究基金(2014D04)，安徽省自然科学基金(1508085SQA198)

The National Natural Science Foundation of China (61370089, 60973125), The Open Research Fund of National Mobile Communications Research Laboratory, Southeast University (2014D04), The Natural Science Foundation of Anhui Province (1508085SQA198)

袁 健： 男，1988年生，博士生，研究方向为代数编码.

朱士信： 男，1962年生，教授，博士生导师，研究方向为代数编码理论、信息安全与序列密码等.

开晓山： 男，1975年生，副教授，研究方向为编码理论与信息安全等.