一个新的超混沌系统及其投影同步
申玉发,刘建平
(河北科技师范学院数学与信息科技学院,河北 秦皇岛,066004)
一个新的超混沌系统及其投影同步
申玉发,刘建平
(河北科技师范学院数学与信息科技学院,河北 秦皇岛,066004)
构造了一个新的超混沌系统,针对该超混沌系统的动力学行为进行了详细分析;然后,给出了基于该系统投影同步的状态观测器,并通过数值仿真探讨了投影同步误差,说明了同步观测器的正确性及有效性。超混沌系统比一般混沌系统的动力学行为更为复杂且难以预测,将其应用在保密通信领域中时具有较高的安全性。
混沌吸引子;平衡点;耗散性;Lyapunov 指数;Lyapunov 维数;投影同步
1963年,Lorenz[1]在研究大气层现象时,偶然发现了混沌吸引存在,自此关于混沌动力学的研究受到学者们广泛关注。时至今日,针对混沌理论的研究已经成为非线性科学的一个研究热点问题,该理论被认为是20世纪人类认识和改造世界的一次新的革命。随着新混沌系统的不断构建和发现,人们对混沌现象研究也更加深入,丰富的混沌理论也促进了混沌系统在通信加密[2~4]、故障诊断[5]等工程领域的应用。目前,国内外研究人员已经提出了许多新的不同类型的混沌系统,如Chen 混沌系统[6],Róssler 混沌系统[7],Qi混沌系统[8],分数阶混沌系统[9],多翼混沌系统[10],最简并行记忆器混沌系统[11],以及各种新超混沌系统[12,13]等。
由于三维混沌系统的结构上较为简单,设计电路较易,因此将其应用于通信加密工程时,加密效果不是很好。其原因主要在于三维混沌的带宽较窄,数字滤波器能滤掉部分混沌序列,导致加密信号容易被破译[14]。而超混沌系统产生的混沌序列信号带宽较宽,能在一定程度上弥补如上不足,在利用混沌同步加密信息处理时,加密的效果会相对较好。
本次研究将提出一个与现有各类混沌系统都是拓扑不等价的新的超混沌系统。通过对其耗散性、平衡点、Lyapunov 指数(简记为LE)和Lyapunov 维数(简记为LD)的动力学特性进行分析,以说明该系统确实是混沌系统。进一步,给出一个基于该系统投影同步的状态观测器,并通过数值仿真探讨了投影同步误差,以表明所给同步观测器的有效性。
1 一个新的超混沌系统及其动力学分析
本次研究构建的超混沌系统的数学模型为
(1)
其中参数a,b,c为实常数。
当取参数a=0.45,b=0.45,c=15时,数值实验表明系统存在混沌吸引子,新超维混沌系统的二维相图如图1所示。
下面,笔者从系统(1)的耗散性和吸引子的存在性、平衡点和稳定性,及其Lyapunov 指数和Lyapunov 维数等3个方面,对系统(1)进行动力学分析。
1.1 系统的耗散性和吸引子的存在性
首先,由于

(2)

其次,方程(2)表明体积元V0在时刻t时收缩为体积元V0e-(a+c)t,即当t→∞时,每个体积元的系统轨迹以速率-a-c逼近到0。最终所有系统轨迹线会被封闭在体积为0的集合上,这恰恰表明了混沌吸引子的存在性。
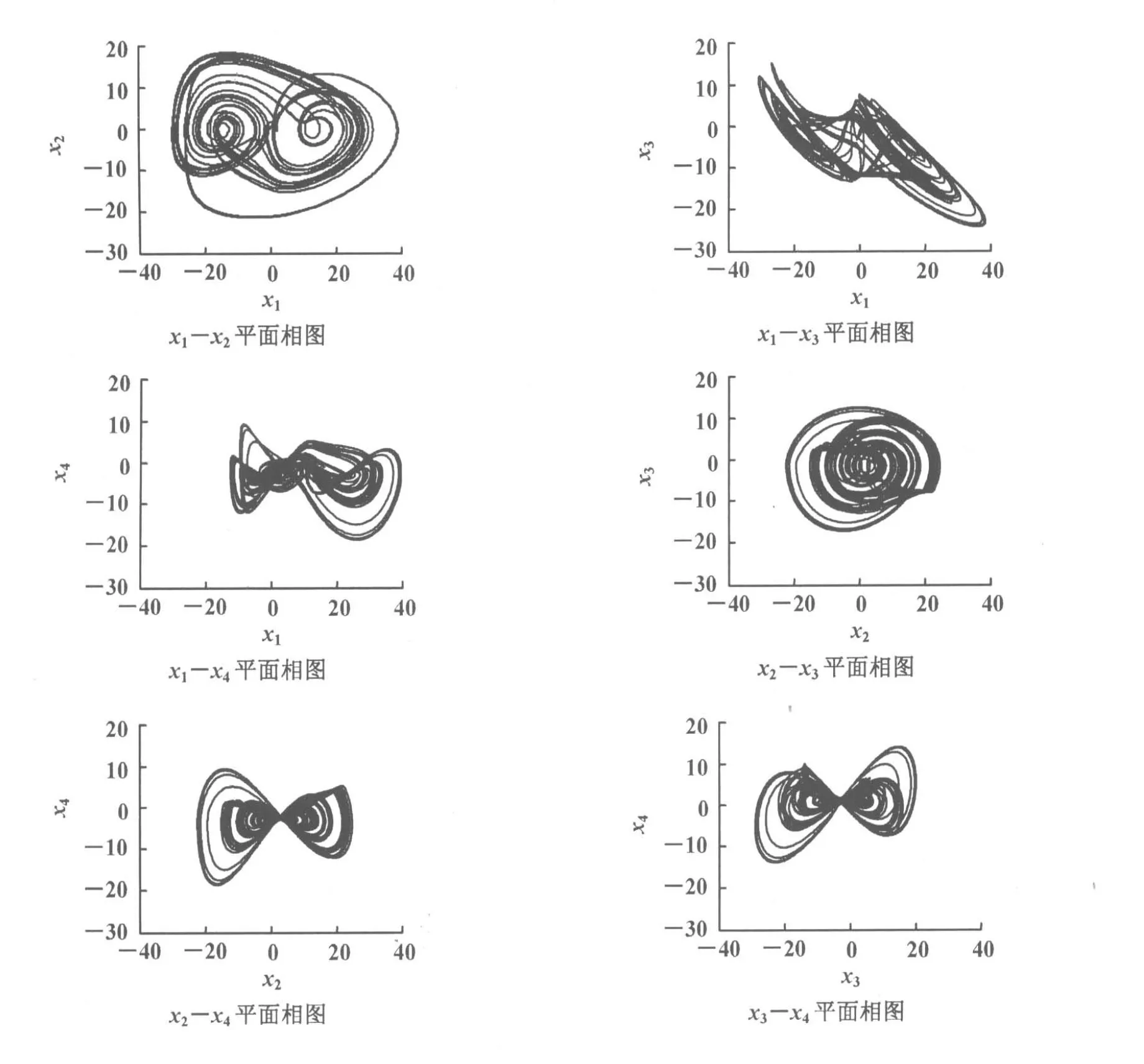
图1 系统(1)吸引子的二维相图
1.2 系统的平衡点和稳定性
系统(1)存在2个非线性项,1个交叉乘积项,1个反正切函数,状态变量分别为x1,x2,x3,x4。为了求解系统(1)的平衡点,令系统(1)的右端为0,得如下方程组
(3)
对(3)求解可得x2=0,x3=0,x4=0,以及

(4)
式(4)为超越方程,0是其平凡解,(4)的非平凡解的解析形式无法得到,只能求其数值解。注意到
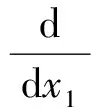
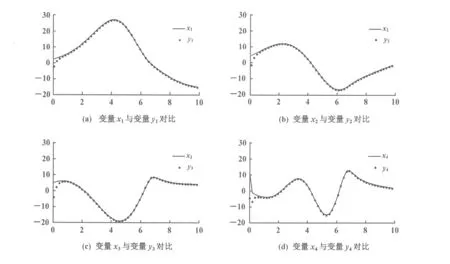
可知arctan(x1)的导函数在x1=0处达到最大值,且最大值为1。因此,当a≥b时,系统(1)具有唯一平衡点S0(0,0,0,0);当a 对于参数a=0.45,b=4.5,c=15,因a S0(0,0,0,0),S1(15.044 2,0,0,0),S2(-15.044 2,0,0,0) 为对系统(1)的平衡点做线性化处理,求系统(1)的雅可比矩阵 对于平衡点S0(0,0,0,0),由det|Js-λI|=0解得Js对应的特征值为 λ1=1.372 4,λ2=-0.911 2+1.456 3i,λ3=-0.911 2-1.456 3i,λ4=-15 其中λ1为正实值;λ2,λ3为负实部的共轭复值;λ4为负实值。 对于非零平衡点S1,S2,即分别对应x1=15.044 2及x1=-15.044 2,均求得Js对应的特征值为 λ1=-0.694 3,λ2=0.122 1+0.777 6i,λ3=0.122 1-0.777 6i,λ4=-15 其中λ1为负实值;λ2,λ3为正实部的共轭复值;λ4为负实值。 如上特征值的形式说明了3个平衡点都是不稳定鞍点。系统(1)的3个不稳定鞍点的存在性进一步表明该系统有可能具有混沌特性。 1.3Lyapunov指数和Lyapunov维数 在混沌系统中,相邻系统轨迹线之间的关系,主要是通过Lyapunov指数LE和Lyapunov维数LD来定量描述。LE的正负个数也是判断系统是不是混沌系统的最重要特征。正的LE说明在初始状态相邻的情况下,随时间的演变,系统的轨线在某方向上会以指数速率分离。因此致使相邻轨线的相关性越来越差,其结构也就变得越来越难以预测,最终呈现出混沌吸引子现象。因此,存在正的LE就可断定系统吸引子的存在,而同时存在2个正的LE且LD不是整数就可以断定系统是超混沌。 利用雅可比矩阵法[15]编译的MATLAB程序,输出新系统的LE指数谱(图2),其中系统(1)的4个LE分别为 LE1=0.120 675,LE2=0.107 688,LE3=-0.670 406,LE4=-15.005 382 而Lyapunov维数 由此可见,系统(1)存在2个正的Lyapunov指数,且LD不是整数,这就说明了系统(1)为超混沌系统。 图2 系统(1)的LE谱 混沌系统的同步控制作为混沌控制的一个非常重要的研究方向,其过程就是通过选择合适的混沌同步控制方法,使两个结构完全相同但初始取值不同的混沌系统,或者两个结构不相同的混沌系统的运动轨迹最终达到渐近一致,即完成同步控制。本节针对所提出的超混沌系统设计一个状态观测器,实现该超混沌系统的投影同步。 2.1 系统的投影同步 为了给出系统(1)投影同步的状态观测器,并探讨其在平衡点处的渐近稳定性,需要借助文献[16]中的一个结论。 引理[16]如果一个n维混沌系统在某个平衡点处的雅可比矩阵的所有特征根λ1,λ2,…,λn均满足|arg(λi)|>π/2(i=1,2,…,n),其中arg(λi)表示λi的辅角,那么这个系统在该平衡点是渐近稳定的。 定理投影比例因子为α,则超混沌系统(1)的投影同步状态观测器可定义为 (5) 证明 在参数a=0.45,b=4.5,c=15时,记 则系统(1)可改写为Dx(t)=Ax+BF(x)。 根据极点配置技术选取反馈增益矩阵K,使A+K的特征值为p=[-5 -5 -5 -5],可得 考虑投影同步误差e(t)=y(t)-αx(t),注意到式(5)可以改写为 Dy(t)=(A+K)y-αKx+αBF(x) 即有 (6) 显然,式(6)是线性的,而且不随时间t的变化而变化。矩阵(A+K)的所有特征值λi=-5(i=1,2,3,4)都满足∣arg(λi)∣>π/2,根据引理可知系统(1)与系统(5)的投影同步误差e(t)=y(t)-αx(t)是渐近稳定的,即 这表明由系统(1)和系统(5)构成的系统满足投影同步。 2.2 系统的数值仿真 令驱动系统为式(1),响应系统为式(5),选取它们的初始点分别为(x1(0),x2(0),x3(0),x4(0))=(3,3,3,3),(y1(0),y2(0),y3(0),y4(0))=(-3,-3,-3,-3)。 这里仅以比例因子α=2为例,模拟系统(1)和(5)投影同步的误差效果(图3)。图3表明,相对应的原系统轨迹曲线与观测器轨迹曲线在很短的时间内趋于重合,系统(1)和(5)达到了投影同步,从数值上证明了所设计的状态观测器是正确且有效的。 图3 比例因子α=2时,系统(1)和(5)投影同步的曲线对比 本次研究构建了一个四维超混沌系统,通过对其动力学行为进行了详细的理论解析,验证了该系统的混沌特性。进一步,设计了一个基于该系统投影同步的状态观测器,并通过数值仿真探讨了投影同步误差,说明了同步观测器的有效性。 [1] Lorenz E N.混沌的本质[M].刘式达,刘式适,严中伟,译.北京:气象出版社,1997. [2] Luo Y L,Du M H.A self-adapting image encryption algorithm based on spatiotemporal chaos and ergodic matrix[J].Chinese Physics B,2013,22(8):080 503. [3] 谢鲲,雷敏,冯正进.一种超混沌系统的加密特性分析[J].物理学报,2005,54 (3):1 267-1 272. [4] 刘乐柱,张季谦,许贵霞,等.一种基于混沌系统部分序列参数辨识的混沌保密通信方法[J].物理学报,2014,63(1):010 501-1-010 501-6. [5] 刘宗华.混沌动力学基础极其应用[M].北京:高等教育出版社,2006. [6] 陈关荣,吕金虎.Lorenz 系统族的动力学分析、控制与同步[M].北京:科学出版社,2003. [7] Rössler O E.An equation for continuous chaos[J].Physical Letters A,1976,57(5):397-398. [8] Qi G Y,Du S Z,Chen G R,et al.On a four-dimensional chaotic system[J].Chaos Solitons & Fractals,2005,23(5):1 671-1 682. [9] 赵品栋,张晓丹.一类分数阶混沌系统的研究[J].物理学报,2008,57(5):2 791-2 798. [10] 胡国四.一类具有四翼吸引子的超混沌系统[J].物理学报,2009,58(6):3 734-3 741. [11] 周小勇.一个新混沌系统及其电路仿真[J].物理学报,2012,61(3):030 504-1-030 504-9. [12] Liu M H,Feng J C.A new hyperchaotic system[J].Acta Physica Sinica,2009,58(7):4 457-4 462. [13] 程杰,张兰.一个新超混沌系统的脉冲修正投影同步[J].湖北民族学院学报(自然科学版),2015,33(2):133-135,138. [14] 唐良瑞,李静,樊冰.一个新四维自治超混沌系统及其电路实现[J].物理学报,2009,58(3):1 446-1 455. [15] 刘扬正,姜长生,林长圣.一类四维混沌系统切换混沌同步[J].物理学报, 2007,56(2):707-712. [16] 王兴元.混沌系统的同步及在保密通信中的应用[M].北京:科学出版社,2012. (责任编辑:朱宝昌) Abstract: The dynamic behavior of hyper-chaos is more complex and unpredictable than the chaos, which usually induces a higher safety when it is applied in the field of communication. In this paper, we constructed a new hyper-chaos and presented a detailed analysis for its dynamic behavior firstly. With the purpose of realizing projective synchronization for the proposed hyper-chaos, we designed a state observer. Finally, we also investigated the error of the projective synchronization. The results of simulation experiment showed that the designed state observer was correct and effective. Keywords:chaotic attractors;equilibrium point;dissipativity;Lyapunov index;Lyapunov dimension;projective synchronization ANewHyper-ChaosandItsProjectiveSynchronization SHEN Yufa,LIU Jianping (School of Mathematics and Information Science & Technology,Hebei Normal University of Science & Technology,Qinhuangdao Hebei,066004,China) O193 A 1672-7983(2017)02-0001-06 10.3969/J.ISSN.1672-7983.2017.02.001 国家自然科学基金项目(项目编号:11571091);河北科技师范学院科学研究基金项目(项目编号:自然科学2017-04)。 2017-06-22 申玉发(1965-),男,博士,教授。主要研究方向:图论及复杂性科学。

2 系统的投影同步与数值仿真
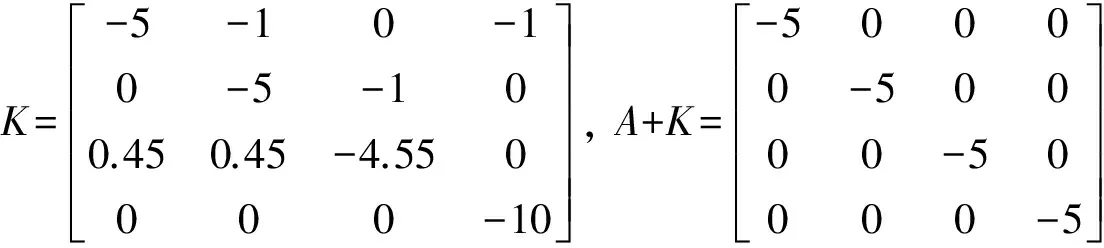

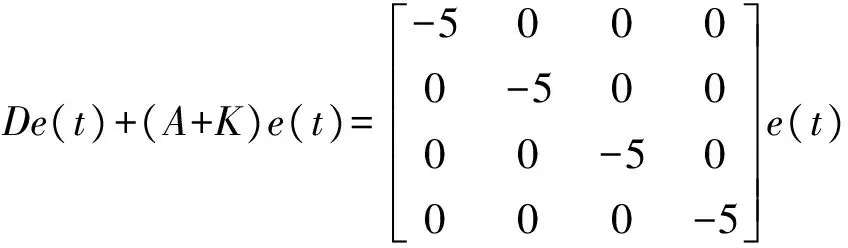
3 结 论

