联合约束级联交互式多模型滤波器及其在机动目标跟踪中的应用
夏小虎 刘 明
联合约束级联交互式多模型滤波器及其在机动目标跟踪中的应用
夏小虎*①②刘 明②
①(合肥学院机械工程系 合肥 230601);②(中国科学院合肥智能机械研究所 合肥 230031)
该文提出一种新型联合约束的级联交互式多模型卡尔曼滤波器,该滤波器由两个滤波器前后两级串联而成;第1级为标准交互式多模型滤波器;第2级为联合约束滤波器。联合约束滤波器的约束条件对第1级滤波器中的多模型集合中各子模型均有效。联合约束滤波器采用平滑约束卡尔曼滤波算法对第1级滤波结果进一步优化。以机动目标实时跟踪为实际工程应用背景,数值仿真和飞行实验结果证明新的联合约束性级联交互式多模型滤波器比标准交互式多模型滤波器具有更小的估计误差和方差,所增计算量合理可行。该文为交互式多模型滤波器和机动目标跟踪两个方向的进一步改进提供了有益借鉴。
机动目标跟踪;交互式多模型;卡尔曼滤波;状态约束方程
1 引言
机动目标跟踪在军事与民用诸多领域有着广泛应用,一直是研究的关注点。目前机动目标跟踪的主流算法是交互式多模型(Interactive Multi- Model, IMM)滤波算法。针对该算法如何进一步提高滤波精度的问题,许多学者提出了各种改进算法,如变结构算法(Variable Structure interactive Multi-Model, VSMM)[9]和自适应算法(Adaptive interactive Multi-Model, AMM)[10],自适应网格模糊算法(Adaptive Grid Fuzzy Multi-Model, AGFMM)[11]等。深入分析不难发现,上述诸多改进算法的共同点是对多模型集合进行各种动态调整,实时改变多模型集合,以适应信号的实时变化,从而达到提高滤波精度的目的。使用这类算法跟踪复杂快速信号,模型集合数必然将增加,计算量从而增加较大。同时,系统复杂度增加,稳定性能和鲁棒性能下降。本文受文献[12]启发,从另一个角度提出对交互式多模型滤波算法的改进。改进思想是从控制对象的状态方程出发,进一步发掘关于控制对象各状态之间相互关系的有用信息,利用该信息建立非线性约束方程,形成联合约束滤波器;对原有交互式滤波结果再进行滤波,从而提高滤波精度;这一思想不妨称为约束滤波。约束滤波的思想来源于文献[12],但该文献只讨论了单模型情况。本文将约束滤波思想推广应用到交互式多模型中,提出一种新型的联合约束级联交互式多模型滤波器(Unified Constrained Cascade Interactive Multi- Model, UCC-IMM)。该滤波器采用前后两级串联结构形式,第1级为标准交互式多模型滤波器。再针对多模型集合中各子模型,建立统一的状态约束方程。基于该约束方程,结合平滑约束卡尔曼滤波算法SCKF(Smoothly Constraint Kalman Filter),形成联合约束滤波器,做为第2级滤波器,对第1级滤波结果做进一步优化。为验证联合约束级联交互式多模型滤波器UCC-IMM的改进效果,针对机动目标实时跟踪这一工程实践问题,进行数值仿真和硬件实验,并与采用标准交互式多模型滤波器IMM进行了对比,结果表明联合约束级联交互式多模型滤波算法UCC-IMM比标准交互式多模型滤波器IMM具有更小的估计误差和估计方差,而增加的计算量合理。本文安排如下:第1节引入研究的理论背景。第2节以机动目标跟踪问题为例建立约束等式;对约束等式的处理方法在第3节介绍。第4节是数值仿真和飞行实验结果分析。最后总结全文。
2 联合约束滤波算法推导
首先分析独立滤波组和联合滤波的利弊,确定采用联合约束滤波器方案。再针对机动目标实时跟踪这一工程实践问题,推导联合约束滤波算法。
2.1 联合约束在多模型滤波器中的位置
交互式滤波包含一组滤波器. 对每一个模型分别进行滤波。在输入端和输出端进行数据交互。那么,新增的非线性约束滤波多模型滤波器的位置应该如何设置呢?可以设想到两种方案,如图1和图2所示。
在图1中,在标准IMM的内部,分别针对多个子模型分别建立约束条件,建立平滑约束滤波器组分别对原滤波器组输出结果再滤波,不妨称为独立约束滤波组。显然,独立约束滤波仍然没有摆脱模型集的框架。如果跟踪复杂快速信号,模型集增加,滤波器组扩大,独立约束滤波组也同样扩大,计算量大大增加,如此难免又陷入各类变结构多模型算法所面临的同样的困境,无法体现改进的创新点和优势。所以,图1方案不可行。
图2中,点虚线中为标准IMM,联合约束滤波器UCF与IMM串联形成联合约束级联交互式多模型滤波器UCC-IMM(点划线范围内)。UCF一次性处理IMM输出交互之后的数据,无论模型集合数量如何增减变化,均不能对联合约束滤波器UCF计算量产生影响,从而避免了图1方案面临的问题。
这一方案的关键之处在于UCF遵循的约束方程满足模型集中的所有子模型。即所有子模型“联合”采用同一个约束滤波器,不再分别独立滤波。这也是本文的创新点所在。
被控对象的状态变化快速而复杂,使用一个数学模型不能准确描述,采用多个子模型构成模型集合描述被控对象不同时刻的状态则更加准确。以飞行器等机动目标跟踪为例,飞行状态最多可以用3个子模型来描述:协调转弯模型、等速模型和加速模型。在可以清楚阐述本文论点的前提下,为简化分析,下面以协调转弯和等速两个模型描述的机动目标跟踪问题为例,建立联合约束方程。

图1 各独立约束滤波器嵌入在IMM中 图2 联合约束滤波器与IMM级联
2.2 协调转弯模型的约束等式
文献[13]提出了机动目标线性离散动态模型:
(1)
显然,相对其他转弯模型,这一模型处理噪声项的手法比较特别。取转弯率受到加性高斯白噪声影响。而其余变量为的函数,就不再考虑噪声干扰。
将等式矩阵(1)的第5行改写为
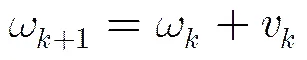
对随机变量取均值:
(3)

(5)
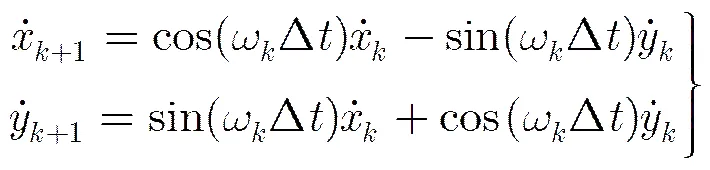
(7)
将此结果再代入式(6),并考虑式(5),可得

(9)
对假设递归一步:

化简可得:
(11)
综合式(6)-式(11),归纳法证明了式(9)假设成立。

这样就获得了对协调转弯模型中状态变量的约束方程。不失一般性,若初始速度状态任意,可推得
(13)
即机动目标在转弯运动中两个速度矢量的平方和为常数;该常数为转弯运动的速度初始值。这个约束对并不是对任意实时状态均有效,只是对平均值成立,不妨称为软约束(Soft Constraints)[12,13]。
2.3 等速模型的约束等式
文献[13]中提出了机动目标在等速飞行时的线性离散动态模型:
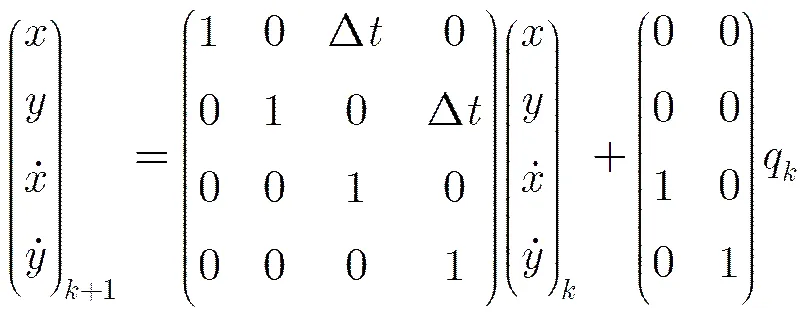
这一模型对噪声的处理手法是在两个速度变量中引入噪声。而两个位置变量为速度的函数,就不再考虑噪声干扰。
考虑到随机变量在均值上下波动,表达式直接可写成
式(15)作为机动目标在等速运动时的状态约束方程。显然,这也是一个软约束(soft constraints)[12,13]。
至此,综合式(13)和式(15),机动目标在协调转弯运动和等速运动两个状态的联合状态约束方程已建立;从上述分析也可以注意到,针对随机系统,对系统变量取均值,更多的是建立软约束。
3 非线性约束等式的处理
式(13)和式(15)均为非线性方程。对于非线性约束,文献[12]列举了多种处理方法。如估计投影法(estimate projection)[15]、系统投影(system projection)[16]、分布概率截断(pdf truncation)[17,18]、平滑约束卡尔曼滤波SCKF(Smoothly Constraint Kalman Filter)[19],移动平均估计MHE(Moving Horizon Estimation)[20]、投影无味卡尔曼滤波(Projected UKF)[21]等。针对文献[12]文中模型,MHE的均方误差最小,但计算量很大。另一方面,实践表明,对于非线性度较高的系统,估计投影等计算量较小的方法可能失效。
综合均方误差和计算量两个因素,本文选用平滑约束卡尔曼滤波SCKF方法来处理非线性约束。该算法借鉴迭代卡尔曼滤波(iterated Kalman Filter)的思想,将约束等式线性化,并作为量测结果代入类似标准卡尔曼滤波更新公式,并多次迭代。具体计算流程见文献[12]和文献[19],此处不再详细展开。
4 数值仿真与硬件实验
采用交互式卡尔曼滤波实现对机动目标状态估计。针对非线性模型,采用扩展卡尔曼滤波EKF (Extended Kalman Filter)[4,5]。
在此基础上,增加平滑约束卡尔曼滤波SCKF方法来处理非线性等式约束式式(13)和式(15)[19],具体步骤见第3节。其中:约束方程的雅克比矩阵采用差分形式;调节参数取。
为验证联合约束级联交互式多模型滤波器(UCC-IMM)对标准交互式多模型滤波器(IMM)改进效果,分别进行了数值计算仿真和实验。现在分别对数值计算仿真和实验的结果和分析论述如下。
4.1 机动目标飞行模态[13]
设机动目标从原点出发,和方向初速度分别为1 m/s和2 m/s,即初始状态。在20 s内进行飞行实验仿真:具体飞行模态如下:第1~4 s内执行等速飞行模态。第4~9 s内执行转弯飞行模态,转弯率=1。第9~11 s内执行等速飞行模态。第11~16 s内执行转弯飞行模态,转弯率。第16~20 s内执行等速飞行模态。采样时间0.1 s,获得200个采样点[13]。
4.2 飞行模型参数设置[13]
4.3 数值仿真结果与分析
图3~图5为单次飞行仿真结果。图中横轴为200个采样点,相邻时间间隔0.1 s。纵轴为各点误差值。
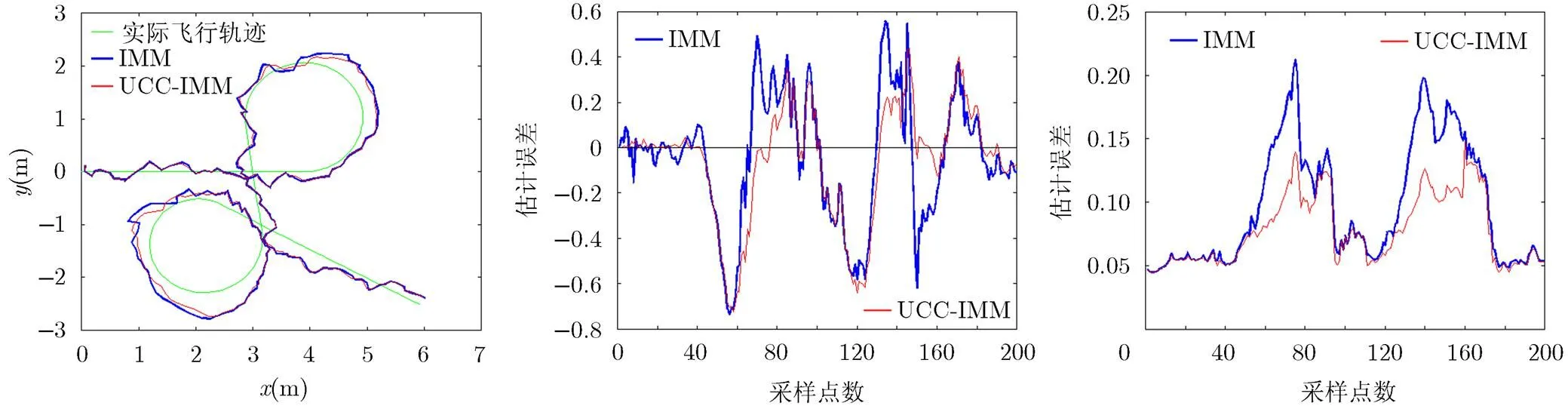
图3 飞行轨迹与量测值 图4 的估计误差对比 图5 的估计方差对比
图3中光滑绿色细线为实际飞行轨迹,蓝色粗线为无约束的标准交互式多模型滤波器(IMM)滤波值,红色细线为联合约束级联交互式多模型滤波器(UCC-IMM)的滤波值。图4是UCC-IMM和IMM对两个速度变量的估计误差对比。图5是UCC- IMM和IMM对转弯率的估计方差对比。
从图3~图5直观上看,UCC-IMM的估计误差和估计方差两个滤波性能指标在整体上比IMM有明显改进。但也不排除在局部点表现较差。下面从对200点取平均值来看UCC-IMM和IMM的滤波性能对比。
设:实际飞行状态向量为;无约束估计状态向量为;有约束估计状态向量为;无约束估计误差向量,估计方差矩阵为;有约束估计误差向量,估计方差矩阵为。
(1)设从UCC-IMM到IMM估计误差的平均下降率:

考虑到UCC-IMM和IMM的估计误差均有正负;对误差均取绝对值处理;这不影响对比分析效果。
(2)设从UCC-IMM到IMM估计方差的平均下降率:
表1从UCC-IMM到IMM估计误差和方差的平均下降率(单次仿真)

变量 (%)11.92 4.5821.927.663.23 (%)39. 6829.4169. 2154. 3419.30
将上述数值仿真实验随机重复多次,统计结果表明上述结论仍成立,如表2所示。
表2从UCC-IMM到IMM估计误差和方差的平均下降率(100次仿真)

变量 (%)8.629.4815.3611.322.88 (%)39.0027.4369.1547.2717.87
数值仿真实验结果显示联合约束级联交互式多模型滤波在估计误差和方差两个方面有明显改进效果。
另外,数值仿真实验也表明,联合约束级联交互式多模型滤波计算量有所增加。分析原因如下:在原有无约束交互式卡尔曼滤波器中,每一个循环过程包括输入交互、卡尔曼滤波、模型概率刷新和联合输出4步。其中,卡尔曼滤波又包括预测和更新两步。采用平滑约束卡尔曼滤波SCKF方法处理约束等式的计算量和更新这一步的计算量相当。总体上计算量增加约30%。增加量合理可接受。
4.4 飞行实验结果与分析
采用微小型四旋翼无人机进行飞行实验,考察联合约束级联交互式多模型滤波器性能的实际改进效果。由飞行姿态控制器和姿态获取模块组成内环控制,由飞行速度和位置控制器和速度信息获取模块组成外环控制。分别采用联合约束级联UCC- IMM和标准IMM对速度信息获取模块输出进行滤波处理。在自动飞行模式下采用GPS模块定位导航平面2维信号。采用声呐模块测量飞行高度。考虑到声呐信号较好,但测量距离有限,只在小范围内进行低空飞行实验。
图6-图7是正常巡航飞行模态下,UCC-IMM和IMM对轴的速度和位置两个变量的滤波效果对比。图中横轴为100个离散数据点,相邻时间间隔0.1 s。纵轴为估计误差值。参考信号选取为GPS信号。飞行实验表明UCC-IMM估计误差整体上优于IMM,和数值仿真的结论一致。
严格来讲,GPS信号本身也受到元件噪声影响,采用单次实验数据做为比较依据并不严谨,因此进一步大量重复实验,在统计意义下考察正常飞行模态时的联合约束级联IMM滤波器的表现。仍然采用和两个指标对位置变量和,速度变量和,以及转弯率等5个指标进行定量统计分析。重复自动飞行和手动飞行的实验多次,对飞行实验结果的统计结果见表3。统计表明,采用联合非线性约束条件对交互式多模型滤波器性能的改进效果明显。
同时,对比表2和表3,可以发现,在实际飞行实验的情况下的改进效果比数值仿真计算效果好。因为实际飞行中存在传感器噪声误差,联合非线性约束方程在原理上对各变量进行了修正,克服了噪声误差的干扰。

表3 UCC-IMM到IMM估计误差和方差的平均下降率(100次飞行实验数据)
5 结束语
本文提出了一种新型联合约束的级联交互式多模型卡尔曼滤波器。联合滤波器的关键点是建立适用于多模型集合中各子模型的联合约束条件。第一,本文建立了针对机动目标跟踪中的等速模型和协调转弯模型的联合约束方程,证明了这一思路的可行性。后续研究可以考虑建立包括等加速模型在内联合约束条件,进一步拓宽联合滤波器在机动目标跟踪中的应用。第二,本文建立的联合约束方程是一种平均意义下的软约束;数值仿真和硬件实验表明这一软约束条件能够改进滤波效果,满足实际工程要求。最后,为进一步提高滤波精度,能否建立和如何建立更好的约束条件,是下一步的研究重点方向之一。
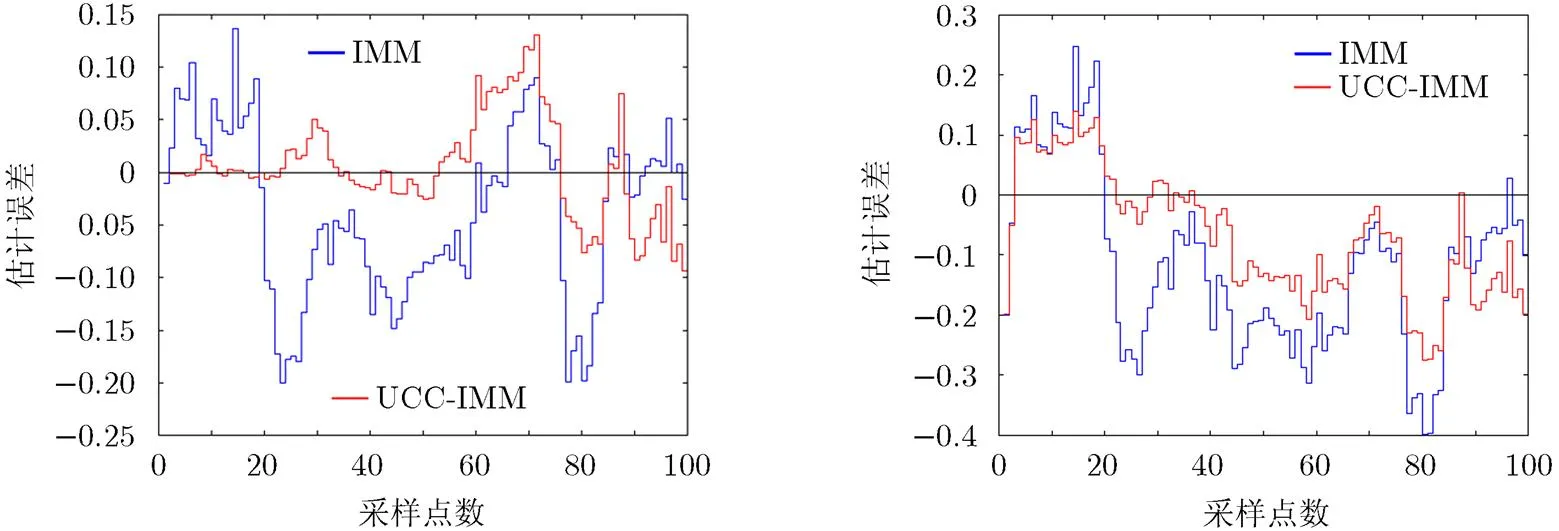
图6 的估计误差对比 图7 的估计误差对比
[1] YANG Jinlong, JI Hongling, and FAN Zhenhua. Probability hypothesis density filter based on strong tracking MIE for multiple maneuvering targets tracking[J].,, 2013, 11(2): 306-316.
[2] LI Bo. Multiple-model Rao-Blackwellized particle CPHD filter for multi-target tracking[J]., 2015, 79(3): 2133-2143.
[3] LIU Meiqin, ZHANG Di, and ZHANG Senlin. Bearing-only target tracking using cubature rauch-tung-striebel smoother [C]. 34th Chinese Control Conference, Hangzhou, China, 2015: 4734-4738.
[4] EVERS C, MOORE A H, NAYLOR P A,. Bearing- only acoustic tracking of moving speakers for robot audition [C]. IEEE International Conference on Digital Signal Processing, Singapore, 2015: 1206-1210.
[5] BECKER S, MUNCH D, KIERITZ H,. Detecting abandoned objects using interacting multiple models[J]., 2015, 96520. doi: 10.1117/12.2195224.
[6] SABORDO M G and ABOUTANIOS E. Enhanced performance for the interacting multiple model estimator with integrated multiple filters[J]., 2015, 94600: 345-349. doi: 10.1117/12.2176180.
[7] MABROUK M B, GRIVEL E, MAGNANT C,. Compensating power amplifier distortion in cognitive radio systems with adaptive interacting multiple model[C]. 23rd European Signal Processing Conference (EUSIPCO), Nice, France, 2015: 1212-1216.
[8] HUANG H, YANG R, NG G W,. Helicopter tracking and classification with multiple interacting multiple model estimator with out-of-sequence acoustic and EO measurements[C]. 19th International Conference on Information Fusion (FUSION), Heidelberg, Germany, 2016: 1132-1139.
[9] KIM T H and MOON K R. Variable-structured interacting multiple model algorithm for the ballistic coefficient estimation of a re-entry ballistic target[J].,,, 2013, 11(6): 1204-1213.
[10] ZHU Zhengwei. Ship-borne radar maneuvering target tracking based on the variable structure adaptive grid interacting multiple model[J]., 2013, 14(9): 733-742.
[11] ZHANG Yuan, GUO Chen, HU Hai,. An algorithm of the adaptive grid and fuzzy interacting multiple models[J]., 2014, 13(3): 340-345.
[12] DAN S and TIEN L C. Kalman filtering with state equality constraints[J]., 2010, 4(8): 1303-1318.
[13] HARTIKAINEN J, SOLIN A, and SARKKA S. Optimal filtering with kalman filters and smoothers a manual for the MATLAB toolbox EKF/UKF[R]. 2011.
[14] 盛骤, 等. 概率论与数理统计[M]. 北京: 高等教育出版社, 1989: 73-75.
SHENG Zhou,. Probability and Statistics[M]. Beijing: High, Education Press, 1989: 73-75.
[15] CHIA T. Parameter identification and state estimation of constrained systems[D]. [Ph.D. dissertation], Case Western Reserve University, 1985, 17-25.
[16] KO S and BITMEAD R. State estimation for linear systems with state equality constraints[J]., 2007, 43(8): 1363-1368.
[17] SHIMADA N, SHIRAI Y, KUNO Y,. Hand gesture estimation and model refinement using monocular camera- ambiguity limitation by inequality constraints[C]. IEEE International Conference on Automatic Face Gesture Recognition, Japan, 1998: 268-273.
[18] SIMON D and SIMON D L. Constrained Kalman filtering via density function truncation for turbofan engine health estimation[J]., 2010, 41(2): 159-171.
[19] DE GEETER J, VAN BRUSSEL H, and DE SCHUTTER J. A smoothly constrained Kalman filter[J].&, 1997, 19(10): 1171-1177.
[20] GOODWIN G, SERON M, and DE DONA J. Constrained control and estimation[M]. Berlin: Springer-Verlag, 2005: 251-262.
[21] JULIER S and UHLMANN J. Unscented filtering and nonlinear estimation[J]., 2004, 92(3): 401-422.
夏小虎: 男,1975年生,副教授,研究方向为信息获取与控制.
刘 明: 男,1955年生,研究员,研究方向为飞行器自动控制.
Unified Constrained Cascade Interactive Multi-model Filter and Its Application in Tracking of Manoeuvring Target
XIA Xiaohu①②LIU Ming②
①(,,230601,);②(,,230031,)
A novel unified cascade constrained interactive multi-model Kalman filter is put forward. The filter is composed of two cascade connected filters, a standard interactive-multiple-model and a unified constrained filter. The latter is effective for everyone in model set of controlled plant and refines the estimation of the former using smoothly constraint Kalman algorithm. Numerical simulation and flying experiments are made for maneuvering target tracking and lower estimated error and covariance are achieved by the unified cascade constrained interactive multi-model Kalman filter compared with conventional interactive multi-model filter. The added computation cost is reasonable and acceptable. The paper is valuable reference for maneuvering target tracking and interactive multi-model filter.
Maneuvering target tracking; Interactive multi-model; Kalman filter; State constraints equation
TN953
A
1009-5896(2017)01-0117-07
10.11999/JEIT160384
2016-04-20;改回日期:2016-12-06;
2016-12-14
夏小虎 xiaxh@hfuu.edu.cn
国家自然科学基金(61340016),安徽省自然科学基金(1408085MF134),安徽省高校优秀青年骨干人才国内外访学研修重点项目(gxfxZD2016224)
The National Natural Science Fundation of China (61340016), Anhui Province Natural Science Foundation (1408085MF134), Anhui Province Youth Leading Talents and Visiting Scholar Key Scheme (gxfxZD2016224)

