一种基于天线布局的姿态测量算法研究
崔建华 程乃平
一种基于天线布局的姿态测量算法研究
崔建华*①②程乃平①
①(装备学院 北京 101416)②(中国人民解放军66407部队 北京 100144)
该文针对姿态测量过程中求解整周模糊度计算复杂度高的问题,提出一种基于天线布局的姿态测量方法。该方法在一定的测量误差下,采用特定的方式配置姿态测量天线组,通过天线配置的约束信息确定载波相位的整周模糊度差,并使用短基线和中基线分别进行姿态粗测和精测,达到快速姿态测量和提高精度的目的。使用这种方法进行飞行器姿态测量时可以不必求解整周模糊度,避免了复杂的整周模糊度搜索算法,进而提高了姿态测量速度,该方法非常适用于飞行器的快速测姿。
导航;姿态测量;整周模糊度
1 引言
GPS卫星的发射信号采用直接序列扩频(DSSS)的调制方式,可以在低信噪比的条件下提供导航服务,导航信号中包含了基本导航数据(如卫星星历及卫星健康状况等)和测距信号,其中的测距信号扩频码分为短的粗捕(C/A)码和长的精密(P)码,C/A码的周期为1 ms, P码是周期长7天的加密序列。通过两种扩频码实现不同精度定位测量。
在进行导航定位的过程中,卫星到用户的伪距是接收机实现单点绝对定位的必要条件,伪距是测距码信号的传播速度乘以测距码从卫星传送到用户接收机天线时所需时间计算出的传播距离。除了伪距之外,接收机从卫星信号中获得的另一个基本测量值是载波相位,它在高精度定位中起着关键作用。在实际应用中,伪距测量和载波相位测量都有很多应用之处。目前接收机伪码测量精度大约为一个码元宽度的千分之一,即:C/A码约为0.3 m,P码约为0.03 m[1]。而载波相位测量由于载波频率高,波长短,所以其测量精度一般可以达到1~2 mm,广泛用于高精度测量定位中。
卫星发射信号的载波是周期性的正弦波,但是在接收机的相位测量只能测得导航信号中不足一周的载波相位小数部分,因此其测量值存在着未知的载波相位整周模糊度[2]。一般在连续跟踪卫星无周跳的情况下,接收机在进行首次测量之后,可以连续测得整周相位变化的卫星载波信号。同时,因为载波相位观测方程最终要完成接收机位置的估算,而参数估计一般使用最小二乘法,所以需要将载波相位观测模型线性化。
在导航卫星姿态测量中,如果将3到5个导航卫星信号接收天线采用天线配置技术安装在飞行器表面,在天线之间基线长度固定的情况下,保证3个以上的天线对天空可视,然后利用各天线接收卫星信号的载波相位观测值,求解在当地水平坐标系下天线间的基线向量,进而确定航天器的姿态角参数。
在实际应用中,每个接收天线在天线平台坐标中的精确位置坐标可以通过事先测量得到,进而可以通过姿态变换矩阵建立基于最小二乘姿态参数的估计模型,从而估算得到最优的姿态角参数[3]。
通过载波相位测量姿态信息具有很高的精度,但其缺点是需要进行整周模糊度的解算,由于解算整周模糊度需要较大的计算量,因此降低了实时性。目前基于载波相位的姿态测量方法大多采用双差法,先求解整周模糊度,然后根据载波相位值进行载体的姿态测量。而在求解整周模糊度时,使用最多的是基于目标函数直接构造搜索空间的LAMBDA方法[4],但这种方法也需要较长的搜索时间。
本文提出了一种基于姿态测量天线配置的新型姿态测量算法,在取得载波相位测量精度的经验值之后,根据天线配置可以直接进行载体的姿态测量,而无需进行整周模糊度的求解。
2 无模糊天线配置模型
无模糊姿态测量方法通天线阵列进行导航信号的接收[5,6],如图1所示,无模糊姿态测量天线阵列为5单元天线阵列,由一个参考阵元A1和两个短基线天线A4, A5以及两个中基线天线A2, A3构成[7]。并按照图中所示配置姿态测量天线阵,其中的短基线姿态测量天线阵(A1A4和A1A5)和中基线姿态测量天线阵(A1A2和A1A3)可以进行不同精度的姿态测量,短基线阵元距参考阵元间距为1,中基线阵元距参考阵元间距为2。短基线天线与中基线天线是共线的。假设入射导航信号与其中一条基线的夹角是。
如果以接收GPS的L1(1575.42 MHz)载波为例,在使用短基线姿态测量天线的情况下,图1中,设计短基线姿态测量天线A4, A5与参考阵元A1的距离1小于等于GPS的L1载波波长的一半,即基线,取1=90 mm。由于A1A4和A1A5各天线间的最大距离小于GPS L1波长,因此,在进行载波相位测量时,对于导航信号的载波相位测量值均在一个整周内,对于参考阵元和短基线姿态测量天线测得的载波相位之间没有整周模糊度。因此可以通过单元天线对入射信号的相位差值求得入射信号的角度,如果每路射频通道载波相位的测量误差最大为,则每路天线基线的入射信号角度测量误差最大为=4/90=0.045 rad。对于姿态测量而言,其姿态测量的角度误差值误差应小于0.045 rad。

图1 无模糊姿态测量天线模型
在此基础上,可以通过中长基线天线阵列进一步提高姿态测量精度,由于通过无模糊短基线天线阵列可初步确定天线阵列的姿态,并且能够将姿态测量误差确定在0.045 rad内,为了进一步提高姿态测量精度,令5单元天线阵列中两短基线单元天线与中基线单元天线共线,构成中基线测量阵。其结构如图1所示,并通过中基线测量阵进一步提高姿态测量精度。


在这种情况下,如果让最大误差值小于半个载波波长,则载波相位的差值就不存在整周模糊度,所以,使得值无模糊的2最大值条件为
(3)

在此条件下,对2间两天线接收的信号进行载波相位测量计算,重新计算信号入射角,则的最大误差可以降低为4 mm/2114 mm=1.9 mrad。如果不考虑计算误差,此时平台的姿态测量精度可达到1.9 mrad。
同理,根据等比计算法则。如果在中基线外再布设长基线测量天线,那么测量精度就能够进一步提高,由于此时精度为1.9 mrad,值无模糊的3最大值条件为

此时的姿态测量精度是4 mm/49979 mm= 0.08 mrad。在整个测量过程中,基线内载波相位差的载波整周模糊度已消除,因此,能够实现快速姿态测量。
我们在理论上分析了实现无模糊姿态测量需要的天线配置方式及精度,在实际应用过程中,测量的精度不仅与载波相位测量误差有关,而且与卫星的几何分布有关,不同的卫星几何分布对定位精度有不同的影响,如果在当前卫星几何分布情况下的精度因子DOP(Dilution Of Precision)为,载波相位的最大测量误差为,那么,值无模糊的短基线1最大值条件为:。基于短基线天线的最大测量误差为:;值无模糊的中基线2最大值条件为:,基于中基线天线的最大测量误差为:;值无模糊的长基线3最大值条件为:,基于短基线天线的最大测量误差为:。
国内某两种型号飞行器的姿态测量指标需求如表1所示。

表1 某型号飞行器姿态测量指标
由以上推算可以得出,在两米基线的情况下,无模糊姿态测量算法的测量精度能够达到小于等于(),能够满足姿态测量的精度需求,另外,无模糊的姿态测量算法还可以应用于大型无人机等飞行器,在小型无人机上应用,因为基线长度要求的限制,其测姿精度将下降至0.045 rad。
3 双差法进行载体姿态测量
在进行姿态测量时,对各阵元天线的信号线等长,并采用统一的时钟通过ADC进行导航信号的采集,并且到各个ADC的时钟线等长,这样可以将信号线误差降到最小,同时对于不同阵元的天线而言,其接收机的钟差是一致的。采用的接收机前端结构如图2所示。

图2 姿态测量接收机前端
接收机接收测量到的GPS载波相位信号包含多种误差,这些误差既包括由于接收机自身因素形成的误差,也包括信号传输过程中形成的误差[8],对于接收机接收到的载波相位而言,接收机测量到的都是载波相位的小数位,其测量值[9]为
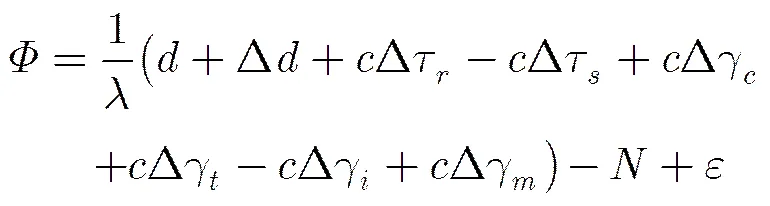
如图3所示如果对编号为A1, A2的两个测量天线对编号为,的两颗导航卫星进行观测,那么对同一卫星的两个天线的载波信号测量值的差值称为单差,对不同卫星的两个单差载波信号测量值的差值称为双差。
那么,对于卫星单差的结果是:

图3 载波相位测姿模型

由于两个测姿天线的距离较近,与天线与卫星的距离相比,其距离非常小,因此,对于两个接收天线而言,针对同一卫星的轨道误差,对流层误差和电离层误差可以认为是相等的[10],即=,,,而且对于同一卫星的时钟误差是一致的,即,所以,式(7)化简为
(8)
对于卫星,进行双差的结果是:
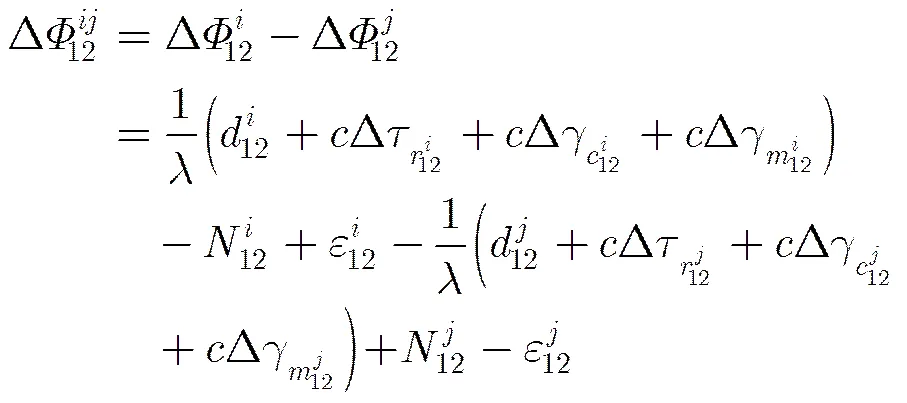
对于不同的导航卫星而言,同一个接收机的接收机时钟误差和接收机信号线误差是一致的,也就是说:,,可以将式(8)简化为
(10)
结合上述的天线构成方式,不考虑多径误差和测量误差的情况,分别对短基线情况和中基线情况予以讨论。
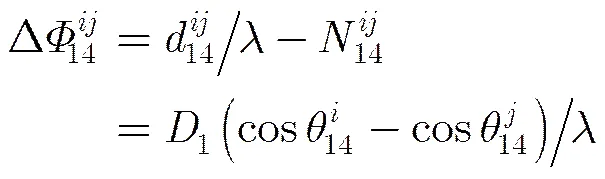
(12)

(14)
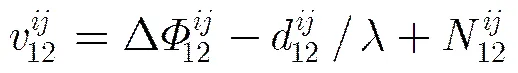
(16)

如果观测到的卫星一共有颗,用每个观测到的卫星与第1颗卫星的观测值进行双差计算,针对于基线A1A2,可以组成-1个方程组成的观测方程组:
(18)
针对于基线A1A3,对于颗可视卫星,可以组成-1个方程组成的观测方程组:

我们按照图4所示建立载体坐标系,以基线A1A2方向作为轴,垂直基线A1A2且与A1A2A3共面的方向为轴,A1为原点,垂直A1的方向为轴。A2A1A3的夹角为(本文中取)。根据前面的分析A1A2= A1A3=2。所以,3个天线的载体坐标系坐标为,,。
在地理坐标系下,根据坐标旋转公式,如果载体的姿态角分别为航向角,横滚角,俯仰角,那么载体坐标和地理坐标的转换关系为
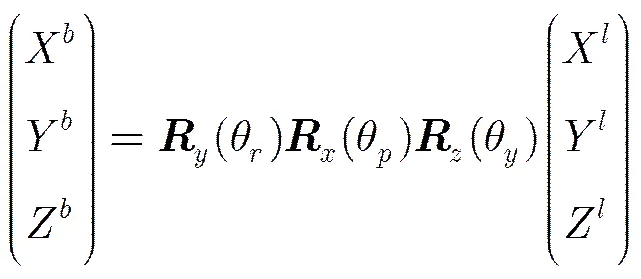
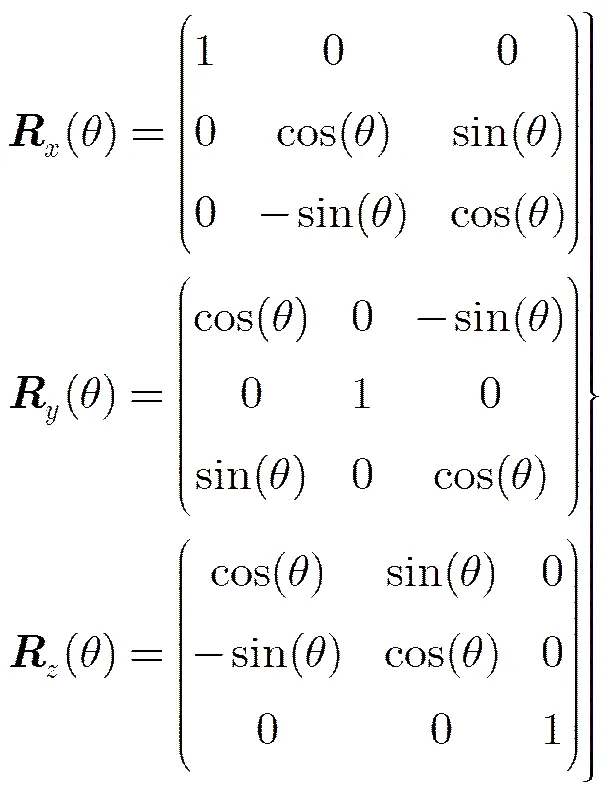
根据载体坐标和地理坐标的转换关系,根据天线A1A2的坐标可以求出航向角和俯仰角:
(22)
再根据天线A3的坐标和求得的航向角与俯仰角,可以求出横滚角:

4 仿真结果
8颗卫星的分布如图5所示。在8颗星的情况下,精度较高,此时精度因子为HDOP=1.4,VDOP=1.9。此时的角测量精度应该为:,仿真结果如图6所示。由图6可以看出,这种方法可以达到分析的精度,具有很高的应用价值。

表2 多星情况下可视星列表

图5 8颗星情况下的可视星座图
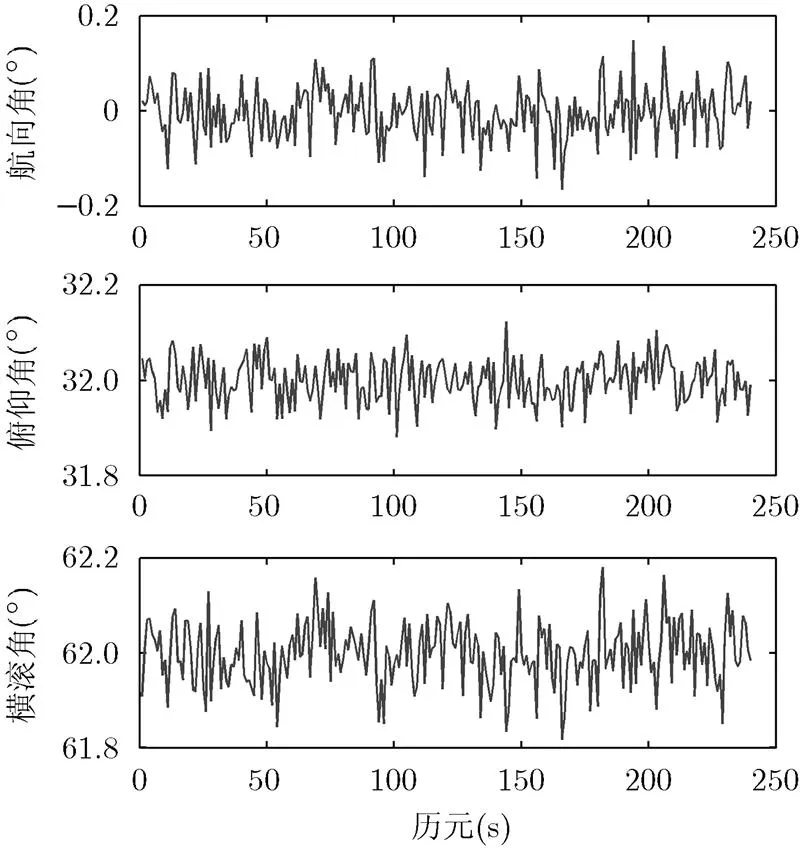
图6 8星姿态解算仿真结果
在可视星为4颗的情况下,可视星如表3所示。4颗卫星的分布如图7所示。
在4颗星的情况下,精度因子有所降低,此时精度因子为HDOP=2.0,VDOP=3.5。此时的角测量精度应为:仿真结果如图8所示。

表3 4星情况下可视星列表

图7 4颗星情况下的可视星座图
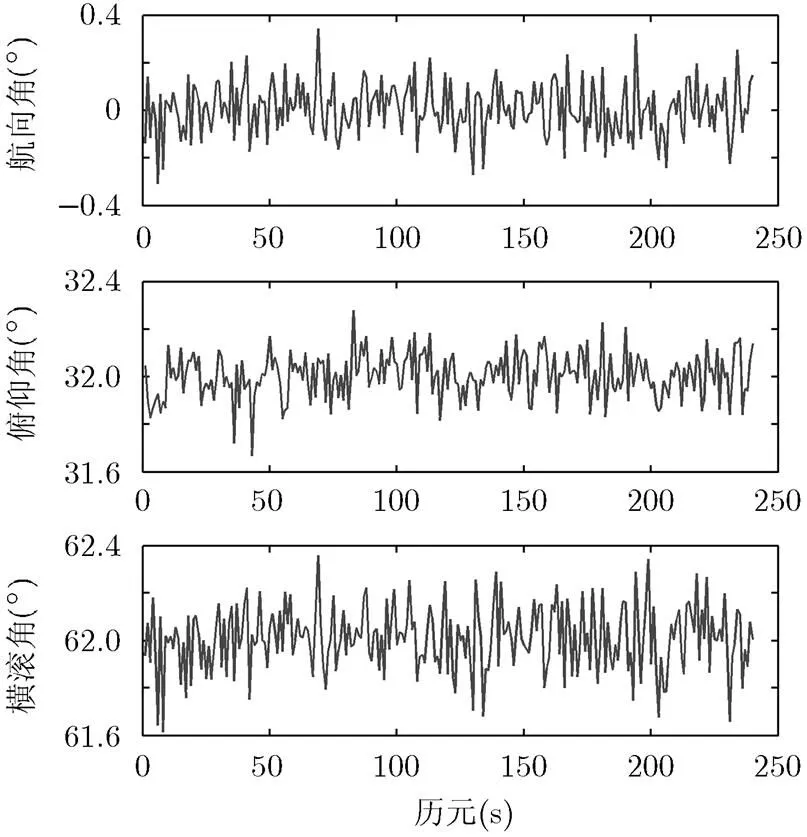
图8 4星姿态解算仿真结果
5 结论
本文提出了一种基于天线位置约束的姿态测量方法,通过对天线位置的约束分析,得出了实现无模糊姿态测量的短基线和中基线模型,并依据此模型建立了双差方程,给出了基于无模糊姿态测量天线的双差姿态解算方法,并给出了仿真结果。
采用本文方法进行载体姿态测量,可以在保证姿态测量精度的前提下缩短姿态测量时间,能够提高飞行器姿态测量的实时性。并且由于无模糊天线的特性保证了在姿态测量时整周模糊度的确定,使得这种方法适用于在高动态飞行器上,只要能够保证载波的正常跟踪,就可以实时进行姿态的测量。
[1] 许江宁, 朱涛, 卞鸿巍. GPS姿态测量技术综述[J]. 海军工程大学学报, 2003, 15(3): 17-22. doi: 10.3969/J.ISSN.1009-3486. 2003.03.005.
XU Jiangning, ZHU Tao, and BIAN Hongwei. Review on GPS attitude determination[J]., 2003, 15(3): 17-22. doi: 10.3969/J.ISSN. 1009-3486.2003.03.005.
[2] 徐定杰, 党超, 沈锋. 一种解算整周模糊度几何算法实现GPS快速测姿[J]. 宇航学报, 2011, 32(12): 2518-2525. doi: 10. 3873/J.ISSN.1000-1328.2011.12.008。
XU Dingjie, DANG Chao, and SHEN Feng. A geometric method for integer ambiguity solution in GPS attitude determination[J]., 2011, 32(12): 2518-2525. doi: 10.3873/J.ISSN.1000-1328.2011.12.008.
[3] CHIANG K, PSIAKI M, and POWELL S. GPS-based attitude determination for a spinning rocket[J]., 2014, 50(4): 2654-2663.doi: 10.1109/TAES.2014.120822.
[4] OLIAZADEH N, LANDRY R, and YESTE-OJEDA O A. GPS-based attitude determination using RLS and LAMBDA methods[C]. IEEE 2015 International Conference onLocalization and GNSS (ICL-GNSS). Gothenburg, Sweden, 2015: 1-7.doi: 10.1109/ICL-GNSS.2015.7217146.
[5] KIS L and LANTOS B. Aided carrier phase differential GPS for attitude determination[C]. 2011 IEEE ASME International Conference on Advanced Intelligent Mechatronics (AIM). Budapest, Hungary, 2011: 778-783.doi: 10.1109/AIM.2011.6027009.
[6] NADARAJAH N, TEUNISSEN P J G, and RAZIQ N. Instantaneous GPS-Galileo attitude determination: single- frequency performance in satellite-deprived environments[J]., 2013, 62(7): 2963-2976.doi: 10.1109/TVT.2013.2256153.
[7] 田增山, 胡小川, 刘丽川。GPS姿态测量系统基线长度和天线布局设计[J]. 电波科学学报, 2001, 16(3): 379-383.doi: 10. 3969/J.ISSN.1005-0388.2001.03.021。
TIAN Zengshan, HU Xiaochuan, and LIU Lichuan. The design of baseline length and antenna configuration for GPS attitude determination system[J]., 2001, 16(3): 379-383.doi: 10.3969/J.ISSN.1005- 0388.2001.03.021.
[8] ARDALAN A A and REZVANI M H. An iterative method for attitude determination based on misaligned GNSS baselines[J].and, 2015, 51(1): 97-107.doi: 10.1109/TAES.2014. 130070.
[9] TATIYAWORANUN C and PURIVIGRAIPONG S. An operational algorithm for satellite attitude determination from GPS carrier phase[C]. IEEE 2012 9th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Hua Hin, Thailand, 2012: 1-4.doi: 10.1109/ ECTICon.2012.6254194.
[10] KOZLOV A, GOLOVAN A, NIKULIN A,. GPS attitude determination under antenna array geometry deformation[C]. 7th International Conference on Recent Advances in Space Technologies. Istanbul, Turkey, 2015: 713-717.doi: 10.1109/ RAST.2015.7208434.
[11] SCATAGLINI T, PAGOLA F, COGO J,. Attitude estimation using GPS varrier phase single differences[J]., 2014, 12(12): 847-852.doi: 10.1109/TLA.2014.6872894.
[12] COIAS J, SANGUINO J, and OLIVEIRA P. Attitude determination using the ambiguity filter with single-frequency L1 GPS receivers[C]. 2012 International Conference on Localization and GNSS (ICL-GNSS). Starnberg, Germany 2012:1-6.doi: 10.1109/ICL-GNSS. 2012.6253133.
[13] 刘根友, 欧吉坤. GPS单历元定向和测姿算法及其精度分析[J]. 武汉大学学报:信息科学版, 2003, 28(6): 732-735.doi: 10.3321/J.ISSN:1671-8860.2003.06.024
LIU Genyou and OU Jikun. Determining attitude with single epoch GPS algorithm and its precision analysis[J].&, 2003, 28(6): 732-735. doi: 10.3321/J.ISSN:1671- 8860.2003.06.024
[14] 杨铁军, 张晓玲, 付毓生, 等. 基于DSP的GPS双天线实时姿态测量系统实现[J]. 电波科学学报, 2002, 17(6): 661-665. doi: 10.3969/J.ISSN.1005-0388.2002.06.024.。
YANG Tiejun, ZHANG Xiaoling, FU Yusheng,. Implementation of GPS twin antennas real-time attitude determination system based on DSP[J]., 2002, 17(6): 661-665.doi: 10.3969/J.ISSN. 1005-0388.2002.06.024.
[15] HENKEL P and IAFRANCESCO M. Tightly coupled position and attitude determination with two low-cost GNSS receivers[C]. 2014 IEEE 11th International Symposium on Wireless Communications Systems (ISWCS), Barcelona, Spain, 2014: 895-900. doi: 10.1109/ISWCS.2014.6933480.
[16] 茅文深, 常传文. 基于导航卫星的载体姿态测量[M]. 北京:国防工业出版社, 2015: 26-35.
MAO Wenshen and CHANG Chuanwen. Carrier Attitude Measurement Based on Navigation Satellite[M]. Beijing: National Defense Industry Press, 2015: 26-35.
Attitude Determination Algorithm Based on Antenna Configuration
CUI Jianhua①②CHENG Naiping①
①(,101416)②(66407,100144,)
In order to solve the problem of high computational complexity of the ambiguity in attitude measurement, a new attitude measurement method based on antenna configuration is proposed. In a certain range of measurement error, the antenna array for attitude determination is properly configured, the integer ambiguity of double difference carrier phase is determined by the constraint information of antenna configuration. Short-baseline and middle-baseline are used for coarse and precise attitude measurement. This method for aerocraft attitude determination does not need to solve the ambiguity. It avoids the use of complex ambiguity search algorithm and improves the speed of attitude determination, it is suitable for fast attitude measurement of aerocraft.
Navigation; Attitude determination; Integer ambiguity
TN967.1
A
1009-5896(2017)02-0459-07
10.11999/JEIT160347
2016-04-11;改回日期:2016-08-30;
2016-10-17
崔建华 cjh_xilinx@163.com
崔建华: 男,1982年生,博士,研究方向为通信与信息系统.
程乃平: 男,1962年生,教授,博士生导师,研究方向为通信与信息系统.

