非理想信道状态下多波束卫星通信的鲁棒安全传输设计

王 舒 达新宇



非理想信道状态下多波束卫星通信的鲁棒安全传输设计

王 舒*达新宇

(空军工程大学信息与导航学院 西安 710077)

考虑多波束卫星通信中存在多天线窃听用户的场景以及非理想信道状态信息带来的系统安全性能恶化，针对合法信道与窃听信道均不理想的多用户MISOME(Multi Input, Single Output, Multi Eavesdropper)系统，该文基于两种类型的信道误差提出了两种鲁棒安全传输方法。在确定误差模型下，利用发送波束成形以及人工噪声协方差的联合优化设计解决系统最差情况安全速率最大化问题(Worst-Case Secrecy Rate Maximization, WC-SRM)问题，通过推导分析将非凸的WC-SRM问题等价为一个1维搜索问题，而这个等价问题的最优解可通过一系列半定规划(SemiDefinite Program, SDP)问题的求解而得到。在统计误差模型下，为求解中断概率约束安全速率最大化(Outage Probability Constrained Secrecy Rate Maximization, OP-SRM)问题，该文提出一种基于WC-SRM的鲁棒安全设计的可靠近似方案。仿真分析验证了该文所提方法的鲁棒性与有效性。

多波束卫星通信系统；物理层安全；安全速率；鲁棒性

1 引言

卫星通信信号由于其广播特性极易被第三方用户窃听，因此卫星通信的安全性与保密性受到了广泛关注。目前卫星通信网络的安全主要依赖传输上层的安全协议来保障，如验证、鉴权和记账(AAA)协议、IP安全(IPSEC)协议以及互联网安全关联与密钥管理协议(ISAKMP)等。但这些协议的安全是通过设计复杂的加解密算法来实现，一旦密钥泄露或被破解，卫星通信的安全则无法保障。利用无线信道的随机性、互易性、差异性的物理层安全技术成为了近年来的研究热点[1,2]。Wyner[3]首先从信息论的角度描述信道的可加密程度，引入保密容量的概念并用来衡量系统的保密性能。文献[4]指出，在高斯广播信道下，当主信道容量大于窃听信道容量时，即保密容量大于零时，认为系统是绝对安全的。然而实际中，窃听者的信道状态一般未知，无法保证其信道容量低于合法用户。为解决这一问题，文献[5]提出一种人工噪声辅助方法来保障系统的保密性。受文献[5]的启发，这种人工噪声辅助方法被广泛应用于MISO[6]以及MIMO[7]系统，通过合理分配有用信号功率与人工噪声功率以达到期望的保密容量。但是上述研究均假设为理想信道状态条件，在实际中这是不太可能的。假设仅窃听信道非理想状态下，文献[8]通过信号与噪声协方差的联合优化，研究了MISO 信道多天线窃听者场景中的鲁棒性安全速率最大化问题。文献[9]又将其扩展到合法信道和窃听信道均为非理想情况下鲁棒性最优波束成形设计。目前国内外有关卫星通信物理层安全的文献较少。文献[10]首先将物理层安全技术引入了多波束卫星通信中，假设仅窃听信道非理想情况下，研究了多用户MISOSE(Multiple-Input Single- Output Single-antenna Eavesdropper)窃听模型中保密速率最大化问题，提出了次优的完全迫零波束成形法。文献[11]考虑了一种更广泛的窃听模型，即存在多个窃听用户的多用户MISOSE模型，在已知部分窃听信道状态信息情况下，引入人工噪声联合设计信号与人工噪声功率，提出了最优的人工噪声辅助的发送方法。然而，文献[11]的方法存在以下问题：(1)在信道的建模中，仅考虑理想的信道状态信息(Channel State Information, CSI)，没有考虑信道状态信息误差可能带来的影响；(2)仅适用于单天线窃听者的情况，没有考虑到多个窃听者协作可构成一个虚拟多天线的窃听者这一不利因素。而文献[8,9]虽然考虑了非理想信道的情况，却只适用于单用户场景，并不能直接应用于多用户多波束卫星通信。

针对上述不足，本文在多用户MISOME (Multiple-Input Single-Output Multiple-antenna Eavesdropper)系统中同时考虑合法CSI误差以及窃听CSI误差分别针对确定误差信道模型以及统计误差信道模型，提出了两种鲁棒的安全传输方法。其目的是，通过对发送波束成形向量与噪声协方差的联合优化，在发送者总功率受限的情况下，分别最大化系统最差情况安全速率(Worst-Case Secrecy Rate, WC-SR)与中断概率约束安全速率 (Outage Probability Constrained Secrecy Rate, OPC-SR)。在非理想CSI条件下，由于WC-SR问题是非凸的，通过分析推导出与其等价的1维搜索问题，这一等价问题的最优解最终可通过一系列的半定规划问题的求解得到。而OPC-SR问题的求解通过推导分析可以转化为WC-SR问题的可靠近似，其求解过程可参考WC-SR问题。

2 系统模型与问题描述

2.1 信道模型

假设卫星工作频率为Ka波段，卫星信号在空中传播时会受到大气内各种物理介质影响，从而引起较大的信号衰减，其中降雨衰减影响最为严重[12]。定义雨衰系数矩阵为, 其中表示为

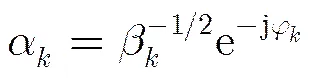
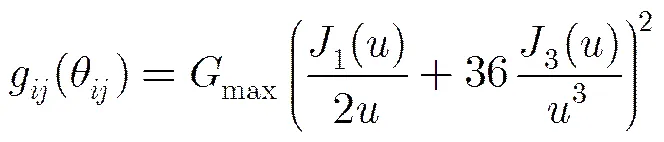
(3)

2.2 人工噪声加扰的信号模型

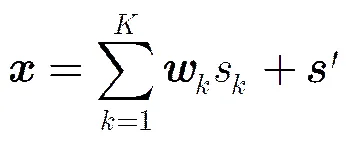
(5)

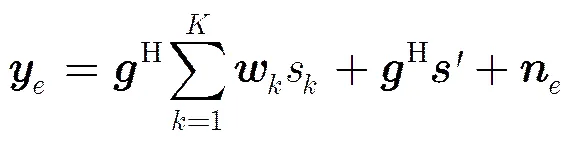
2.3 问题描述

根据上述信号模型，用户可以获得的安全速率为

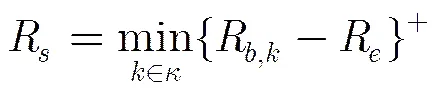
(8)

(10)

式中，为Alice的最大发送功率。在Alice已知理想合法信道以及窃听信道的条件下，该问题为非凸的，其求解方法可以参考文献[11]。但由于量化误差、反馈延迟、多普勒频移等影响，Alice不可能获得完整的信道状态信息，因此建立非理想的信道状态信息的模型，研究合法信道与窃听信道同时存在误差时鲁棒的安全速率最大化问题是非常必要的。

3 非理想信道状态下鲁棒的安全传输方法

本节中，根据文献[14]，当地球站的位置已知时，即已知下行链路的信道特征，这样其信道雨衰系数矩阵就可以估计得到。因此当Alice已知所有Bob和Eve的位置时，由式(3)可分别估计出合法信道与窃听信道，考虑存在信道估计误差时，将合法信道与窃听信道分别表示为

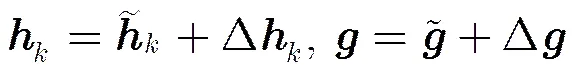
3.1 基于确定误差信道模型下的鲁棒安全传输方法

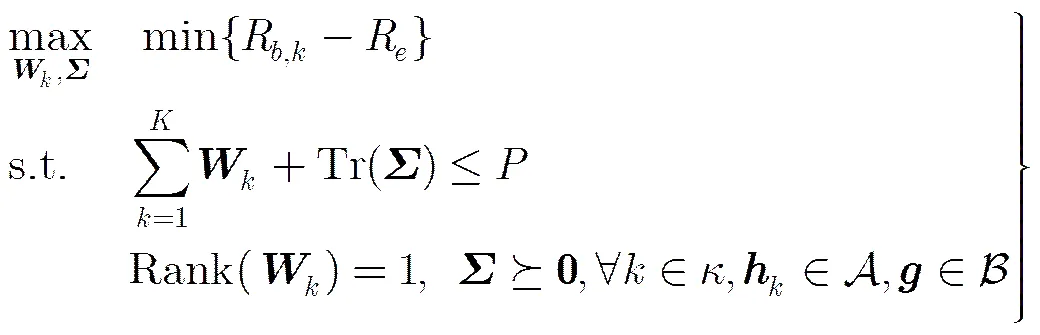
(13a)

(13c)

(13d)

上述问题式(13)是非凸的，首先，将目标函数化简，定义变量，由于对数函数是递增的，因此去掉对数函数后

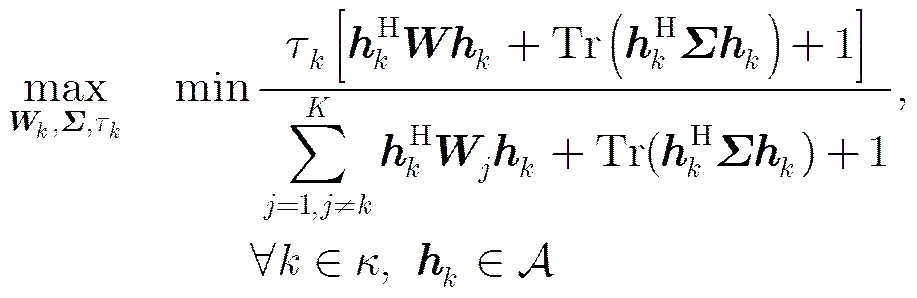
而由于问题式(13)其中的约束条件式(13b)是非凸的且难以计算，需对其进行转化，由，得到

(15)

引理1[16]对于任一厄密特(Hermit)矩阵，令，当且仅当时，有

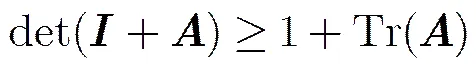
将其应用于式(15)，则约束条件式(13b)可转化为一个凸不等式。

(17)

也就是说，式(17)是式(13b)的一个松弛形式，用式(17)代替式(13b)构成WCR-SRM问题的可行解更多。而当，则上式是等价的。将式(14)和式(17)代入问题式(13)，得到松弛后问题：

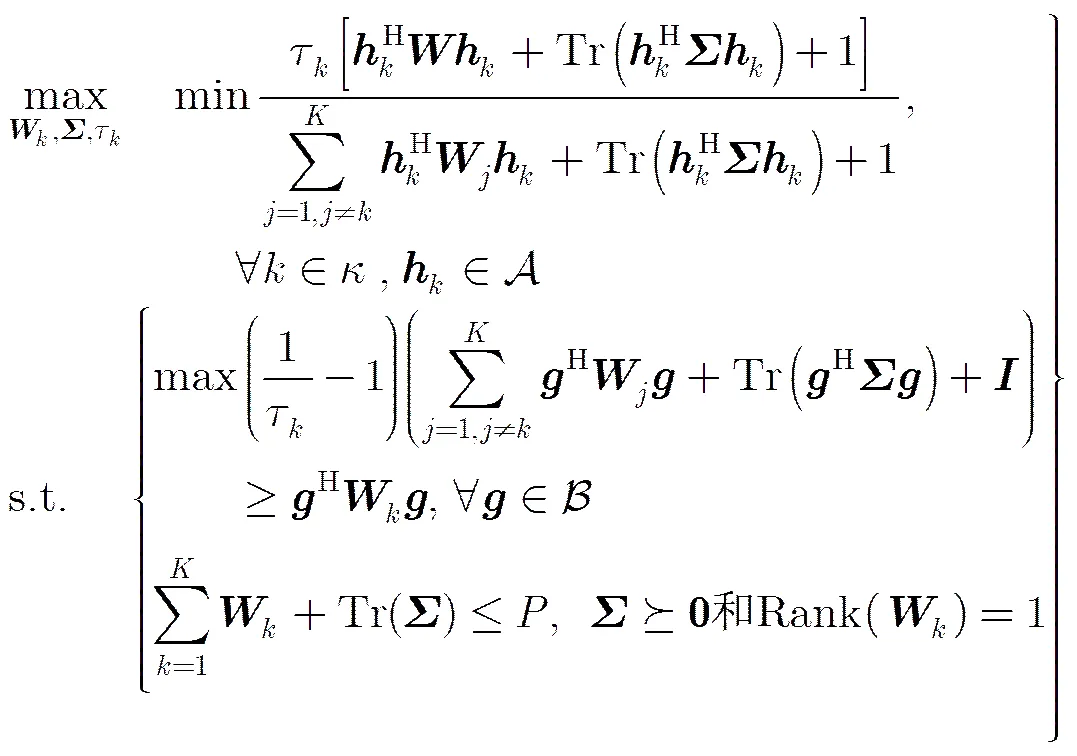
(19)

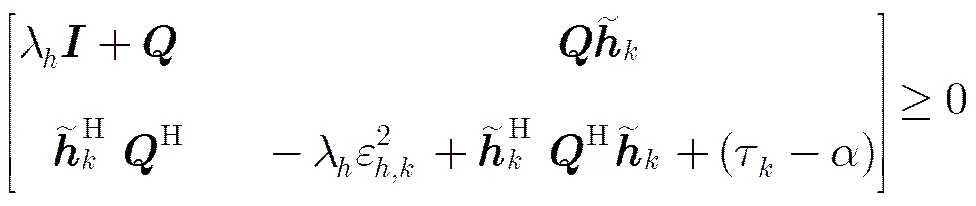
引理2[19]对于任一厄密特(Hermit)矩阵，令且，则式(21)是等价的。

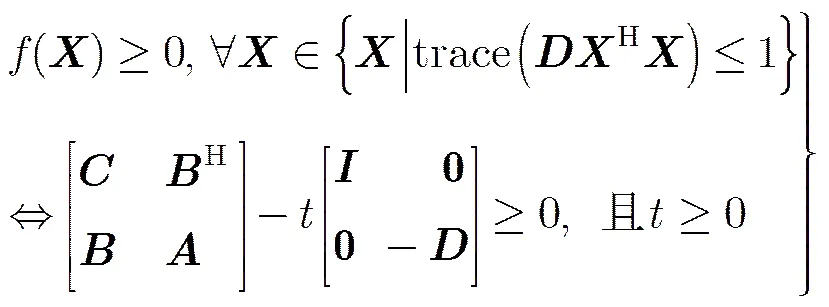
利用引理将问题式(19)中的约束条件3进行转化，于是约束条件等价表示为

(22)

最终，用式(20)和式(22)分别替换问题式(19)中的约束条件1和约束条件2，得到表述式：

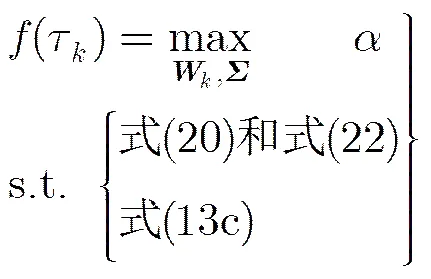
(24)

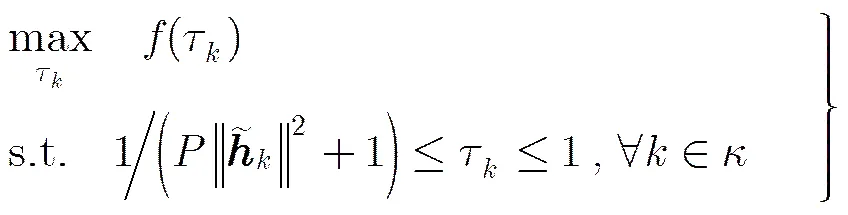
3.2 算法描述

容易看出，很多的1维搜索方法[16,20]可用于搜索问题式(25)的最优解。本文采用无需求导的黄金分割法进行求解，一方面其计算复杂度较低，另一方面至少可以保证一个局部最优解。同时，在进行1维搜索的过程中，本文利用现有的优化工具包CVX对优化问题式(23)进行求解。具体来说, 优化问题式(23)的最优解可以通过二分法在包含其最优值的区间内搜索得到。下面讨论两个比较重要的问题: 一个是如何选取；另一个是优化问题式(23)的最优解与原优化问题式(25)的最优解的关系。

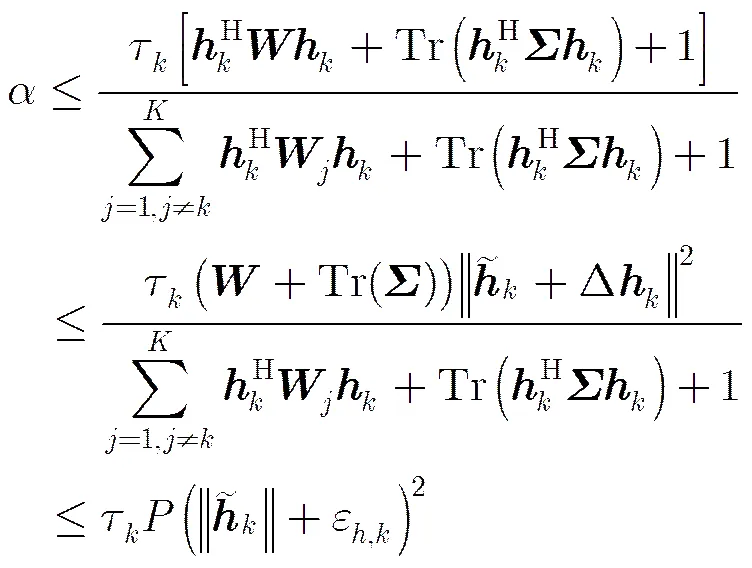
(27)

然后讨论优化问题式(23)的最优解与原优化问题式(13)的最优解的关系，采用秩松弛去掉秩1约束必将导致优化问题式(13)的可行解空间变大。因此，优化问题式(23)的最优值并不一定为秩1的解。如果问题式(23)的最优解的秩均为1，即满足，也就说明采用秩松弛没有损失原优化问题的最优性，同时保证了式(17)等价于式(13b)，此时最优解可以通过对进行特征值分解，其主特征向量作为最优波束成形向量。另一方面, 如果优化问题式(23)的最优解不全为1(即存在大于1的解)，则可以利用文献[19]提出的高斯随机化方法来获得优化问题式(23)的近似解。

根据上述分析，优化问题式(13)的最优解，即发送端最优波束成形矢量可以通过表1获得。

3.3 基于统计误差信道模型下的鲁棒安全传输方法

上一节的WCR-SRM问题是一个在确定信道误差范围内的绝对安全传输设计问题。在本节中，在统计信道误差模型下，信道误差是一个满足一定概率分布的随机的值，即误差范围是不确定的，因此很难对其进行绝对的安全传输设计。然而，可以采用中断概率准则对其进行安全传输设计，系统的中断约束鲁棒安全速率最大化(Outage-Constrained Robust Secrecy Rate Maximization, OCR-SRM)问题可描述为

表1 确定误差模型下鲁棒安全传输算法

(30)

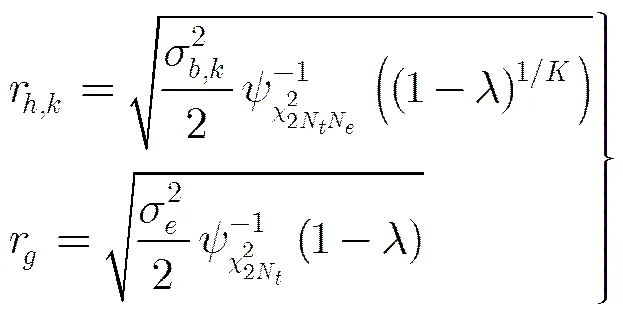
(32)

于是，得到问题式(28)的可靠近似

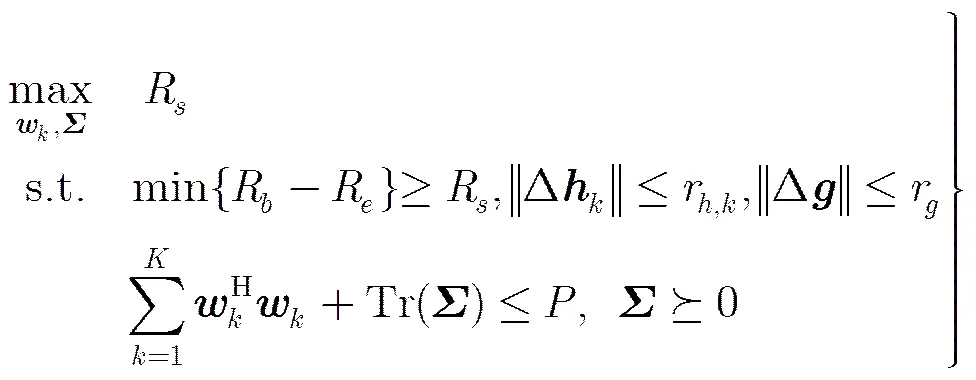
也就是说，问题式(33)的可行解同样适用于问题式(27)，同时，观察发现，当,时，问题式(33)等价于确定误差模型下的WCR-SRM问题式(13)，所以问题式(33)的求解方法可以参照3.1节，不再赘述。

4 仿真实验

为了验证本文方法的保密性能，下面通过与文献[11]方法的比较，其主要区别在于本文同时考虑了主信道与非法信道的误差，而文献[11]将带有估计误差的CSI看作为理想的CSI，进行安全速率最大化设计。仿真参数设置如下：发送天线，合法用户数，窃听天线。地球站与卫星仰角为，波束直径，其中合法用户地球站在以内随机分布。在Ka频段内，第个合法用户信道估计与窃听信道估计均由式(3)计算得到，其中3 dB功率损耗角，雨衰因子。定义合法信道与窃听信道误差比分别为,，该值越大说明对应的信道估计偏差越大。

首先，在确定误差模型下比较文献[11]与本文方法的最差情况安全速率。如图1(a)所示，无论是文献[11]方法还是本文方法，固定(或者)，随着(或者)的增大，系统安全速率逐渐降低。但在相同误差比下，本文方法安全速率均高于文献[11]方法，这也验证了本文方法对于合法信道误差和窃听信道误差的鲁棒性，且发送功率越大，越能体现本文方法的有效性。同时观察发现，无论是文献[11]方法还是本文方法，,时的系统安全速率低于,时的系统安全速率，也就是说合法信道的误差比对于系统安全速率的影响大于窃听信道对于系统安全速率的影响，这是由于式(24)中有关合法信道的约束条件共有2个，而窃听信道的约束条件只有一个。当,,时本文方法的系统安全速率优于文献[11]方法，而当,,时本文方法则比文献[11]方法高出，说明信道误差越大本文方法的优越性越明显。图1(b)中给出了确定误差模型下，发送功率时文献[11]方法与本文方法的最差情况安全速率与信道误差比或的关系。观察发现，随误差比或的增大，本文方法系统WCSR都高于文献[11]方法的WCSR，这也进一步验证了本文方法对于信道误差鲁棒性。同时发现，当或大于0.25时，本文方法的WCSR趋于一个稳定值，而文献[11]方法的WCSR仍随误差比的增大不断降低。而窃听信道误差比时，本文所提方法与文献[11]方法之间安全速率的差距大于窃听信道误差比时的差距，这也验证了图1(a)中合法信道的误差比对于系统安全速率的影响大于窃听信道对于系统安全速率的影响。

下面分析在统计误差模型下本文所提方法的中断安全速率。图2(a)为不同中断安全速率与最大发送功率之间的关系，如图所示，系统中断安全速率随着的增大而增大，随误差变量方差或的增大而减小，但同时观察发现，误差变量方差或变化对系统安全速率的影响大于的变化的影响，这与计算误差半径的式(30)有直接关系。当,时的系统安全速率低于,时的系统安全速率，也就是说合法信道的误差比对于系统安全速率的影响大于窃听信道对于系统安全速率的影响，这是由于中断安全速率的计算为最差情况安全速率的近似。图2(b)中给出了统计误差模型下，发送功率时不同情况下本文方法的中断安全速率与信道误差变量方差或的关系。无论为何值，时的系统中断安全速率均大于时的，这也与图2(a)中的结果相一致。

5 结束语

针对合法用户CSI与窃听用户CSI均不理想导致多波束卫星通信系统安全性能恶化，基于两种信道误差模型本文分别提出了两种多用户MISOME系统的鲁棒安全传输方法。在确定误差模型下，通过发送波束成形以及人工噪声协方差的联合优化设计解决系统WC-SRM问题，由于该问题为非凸的，通过将非凸的约束条件替换为确定的凸约束条件，最终转化为一个半定规划(SemiDefinite Program, SDP)问题和一系列1维搜索问题对其进行求解。仿真结果表明，相较已有方案，本文方法的安全性能得到明显的提升，同时发现合法用户的信道误差比窃听用户的信道误差对系统安全性能的影响更大。在统计误差模型下，为求解OP-SRM问题，本文提出一种基于WC-SRM的鲁棒设计的可靠近似方案。仿真结果表明，所提方案为OP-SRM问题的次优解。

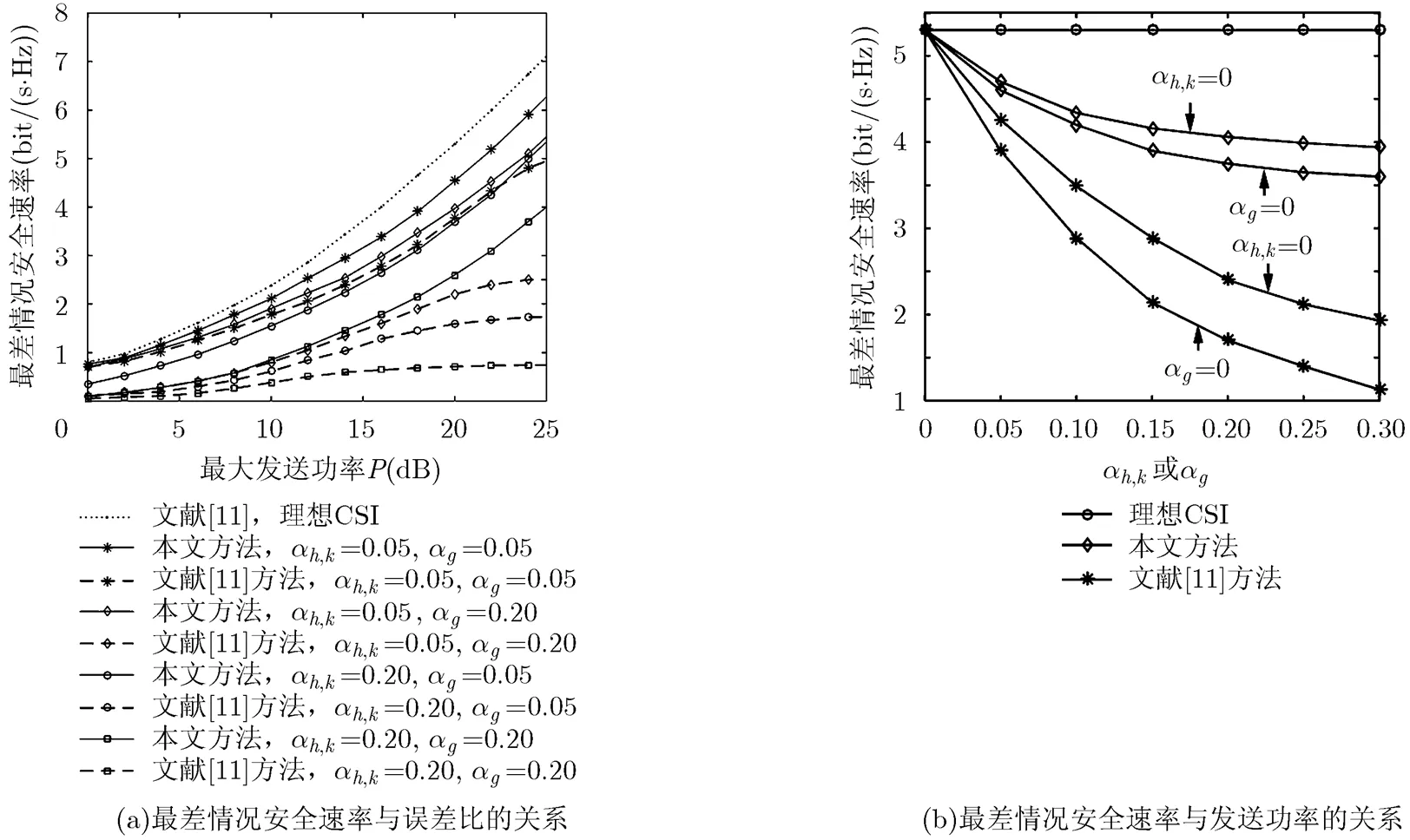
图1 确定误差模型系统安全性能比较

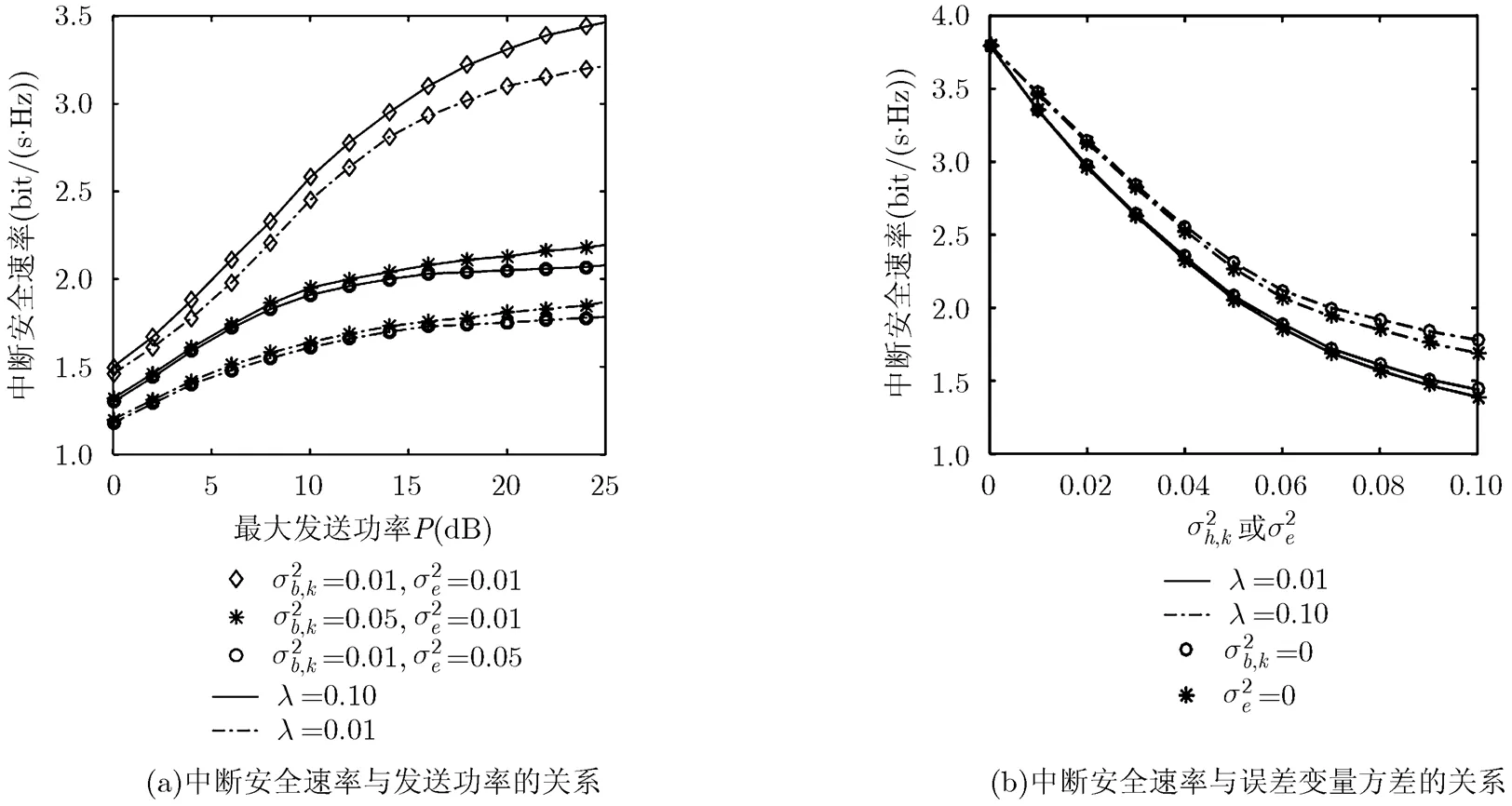
图2 统计误差模型系统安全性能比较

[1] ZHANG Xi, MCKAY M R , ZHOU Xiangyun,.Artificial-noise-aided secure multi-antenna transmission with limited feedback[J]., 2015, 14(5): 2742-2754. doi: 10.1109/TWC.2015.2391261.

[2] LI Na, TAO Xiaofeng, and XU Jin. Artificial noise assisted communication in the multiuser downlink: optimal power allocation[J]., 2015, 19(2): 295-298. doi: 10.1109/LCOMM.2014.2385779.

[3] WYNER A D.The wire-tap channel[J]., 1975, 54(8): 1355-1387.doi: 10.1002/j.1538-7305.1975.tb02040.x.

[4] CSISZAR I and KOMER J. Broadcast channels with confidential messages[J]., 1978, 24(3): 339-348.doi: 10.1109/TIT.1978.1055892.

[5] GOEL S and NEGI R. Guaranteeing secrecy using artificial noise[J]., 2008, 7(6): 2180-2189.doi: 10.1109/TWC.2008.060848.

[6] WANG Huiming, ZHENG Tongxin, and XIA Xianggen. Secure MISO wiretap channels with multiantenna passive eavesdropper artificial noise vs. artificial fast fading[J]., 2015, 14(1): 94-106.doi: 10.1109/TWC.2014.2332164.

[7] LIU Shuiyin, HONG Yi, and VITERBO Emanuele. Guaranteeing positive secrecy capacity for MIMOME wiretap channels with finite-rate feedback using artificial noise[J]., 2015, 14(8): 4193-4203. doi: 10.1109/TWC.2015.2417886.

[8] TANG Yanqun, XIONG Jun, MA Dongtang,. Robust artificial noise aided transmit design forMISO wiretap channels with channel uncertainty[J]., 2013, 17(11): 2096-2099. doi: 10.1109/LCOMM.2013. 100713.131673.

[9] LI Qiang and MA Wingkin. Spatially selective artificial-noise aided transmit optimizationfor MISO multi-eves secrecy rate maximization[J]., 2013, 61(10): 2704-2717. doi: 10.1109/TSP.2013. 2253771.

[10] JIANG Lei, ZHU Han, María Ángeles Vazquez-Castro,. Secure satellite communication systems design with individual secrecy rate constraints[J]., 2011, 6(3): 661–671.doi:10.1109/TIFS.2011.2148716.

[11] GAN Zheng, ATHANASIOS D, and OTTERSTEN Bjorn. Physical layer security in multibeam satellite systems[J]., 2012, 11(2): 852–863. doi:10.1109/TWC.2011.120911.111460.

[12] DESTOUNIS A and ATHANASIOS D. Dynamic power allocation for broadband multi-beam satellite communication networks[J]., 2011, 15(4): 380–382.doi: 10.1109/LCOMM.2011.020111.102201.

[13] 赵家杰, 彭建华, 黄开枝, 等. 基于人工噪声的多用户 MIMO 系统加密算法[J]. 电子与信息学报, 2012, 34(8): 1939–1943.doi: 10.3724/SP.J.1146.2011.01068.

ZHAO Jiajie, PENG Jianhua, HUANG Kaizhi,. A multi- user MIMO system encryption algorithm based on artificial noise[J].&, 2012, 34(8): 1939–1943. doi: 10.3724/SP.J.1146.2011.01068.

[14] ZHU Jun, SCHOBER Robert, and BHARGAVA V K. Linear precoding of data and artificial noise in secure massive MIMO systems[J]., 2016, 15(3): 2245–2261. doi: 10.1109/TWC.2015.2500578.

[15] LI Qiang, MA Wingkin, and SO Anthony Mancho. A safe approximation approach to secrecy outage design for MIMO wiretap channels[J]., 2014, 21(1): 118-121. doi:10.1109/LSP.2013.2293884.

[16] LI Qiang and MA Wingkin. Optimal and robust transmit designs for MISO channel secrecy by semidefinite programming[J]., 2011, 59(8): 3799-3812.doi:10.1109/TSP.2011.2146775.

[17] LUO Zhiquan, MA Wingkin, SO Anthony Mancho,. Semidefinite relaxation of quadratic optimization problems [J]., 2010, 27(3): 20-34.doi:10.1109/MSP.2010.936019.

[18] DATTORRO J.Convex Optimization and Euclidean Distance Geometry[M]. Meboo Publishing USA, 2005: 404-410.

[19] LUO Zhiquan, STURM F, and ZHANG Shuzhong. Multivariate nonnegative quadratic mappings[J]., 2004, 14(4): 1140-1162.doi:10.2139/ssrn.545582.

[20] KOLDA T, LEWIS R, and TORCZON V. Optimization by direct search: new perspectives on some classical and modern methods[J]., 2003, 45(3): 385-482. doi: 10.1137/S003614450242889.

[21] XIONG Jun, MA Dongtang, WONG Kaikit,. Robust masked beamforming for MISO cognitive radio networks with unknown eavesdroppers[J]., 2016, 65(2): 744-755.doi:10.1109/TVT.2015. 2400452.

Robust Secure Transmit Methods for Multibeam Satellite Communication with Imperfect Channel State Information

WANG Shu DA Xinyu

(,,’710077,)

Considering a general eavesdropping case where the eavesdropper is equipped with multiple antennas and two uncertainty models for the imperfect Channel State Information (CSI) on the main and eavesdropper’s channels at the transmitter. Two robust transmission methods are proposed for multiuser Multiple-In, Single-Out, Multiple-antenna Eavesdropper (MISOME) systems to provide SINR guarantee for the legitimate user by the optimization of beamforming and artificial noise covariance matrix. For the deterministic uncertainty model, the Worst-Case Secrecy Rate Maximization (WC-SRM) problem is derived an equivalent problem of the WC-SRM problem through analysis. The equivalent problem can be recast as a single-variable optimization problem, which can be handled by solving a sequence of convex SemiDefinite Programs (SDPs). For the stochastic uncertainty model, a suboptimal scheme to solve the Outage Probability constrained Secrecy Rate Maximization (OP-SRM) problem is proposed based on the robust design for the WC-SRM problem. Finally, the effectiveness and the robustness of the proposed algorithms are validated by the simulation results.

Multibeam satellite communication; Physical layer security; Secrecy rate; Robustness

TN927

A

1009-5896(2017)02-0342-09

10.11999/JEIT160429

2016-04-29；改回日期：2016-09-23；

2016-11-16

王舒 xss_wang@163.com

国家自然科学基金(61271250, 61571460)

The National Natural Science Foundation of China (61271250, 61571460)

王 舒： 女，1987年生，博士生，研究方向为物理层安全和卫星通信.

达新宇： 男，1961年生，博士生导师，研究方向为卫星通信和通信信号处理.