对N次观测Pareto分布参数有效估计范围的扩展

胡 冲 罗 丰 张林让 范一飞 陈帅霖



对次观测Pareto分布参数有效估计范围的扩展

胡 冲 罗 丰*张林让 范一飞 陈帅霖

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

基于方法的次观测Pareto分布参数估计不能有效估计形状参数小于1的情形。该文采用方法对基于的方法进行扩展，将次观测Pareto分布的形状参数的有效估计范围进行扩大。文中推导了次观测Pareto分布参数估计的表达式，从理论上证明该方法能够估计小于1的形状参数。仿真结果表明：时，方法能够在该扩大的范围内有效地估计形状参数。

参数估计；雷达杂波；Pareto分布；次观测

1 引言

为了提高信杂比(Signal-to-Clutter Ratio, SCR)，雷达信号处理机往往会对一个相干处理间隔(Coherent Processing Interval, CPI)内的次观测回波信号进行相参或非相参积累[1]，积累后杂波模型的准确性会直接影响目标的检测性能。而近年来的研究工作表明Pareto分布是一种较K分布及与其相关修正分布(KA, KK等)更具优势的统计杂波模型，因此对次观测Pareto分布的参数进行准确估计对提高雷达的目标检测性能具有十分重要的意义。

传统的最大似然估计(Maximum-Likelihood Estimation, MLE)法对单次观测Pareto分布的形状参数的估计是其尺度参数的函数，然而其尺度参数的估计没有闭合解，参数估计需要用数值方法寻找方程零点，计算比较低效[12]；而传统的矩估计法(Method of Moments, MoM)，如一二阶矩法，由于计算二阶矩时Gamma函数在形状参数小于2的时候无意义，因此该方法不能有效估计真值小于2的形状参数[13,14]；文献[14]在借鉴了基于方法的K分布参数估计后，提出将该方法用于Pareto分布的参数估计，该方法较一二阶矩法形状参数的有效估计范围扩大到了真值大于1的情形，然而由于基于的方法需要计算的Diagram函数在形状参数小于1时无意义，因此该方法不能有效估计小于1的形状参数。本文借鉴文献[14]与文献[15]，对基于的方法进行扩展，采用基于的方法对次观测Pareto分布参数进行估计，将形状参数的有效估计范围进一步扩大到大于的情形。仿真实验结果表明，在的情况下，该方法较一二阶矩法和法能够对形状参数更加有效估计，因此对形状参数的有效估计范围进行了扩大。

2 N次观测Pareto分布

海杂波的复合模型是通过结构分量对散斑分量进行调制得到的。

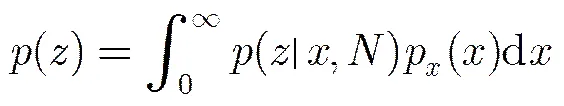
次观测的散斑分量模型为形状参数为的Gamma分布，其概率密度函数(PDF)为

(2)

(4)

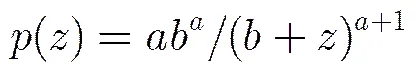
为广义Pareto II型或Lomax分布PDF。通过变换与后，单次观测的广义Pareto II型分布PDF也可以写为

(6)

3 参数估计

3.1 一二阶矩估计

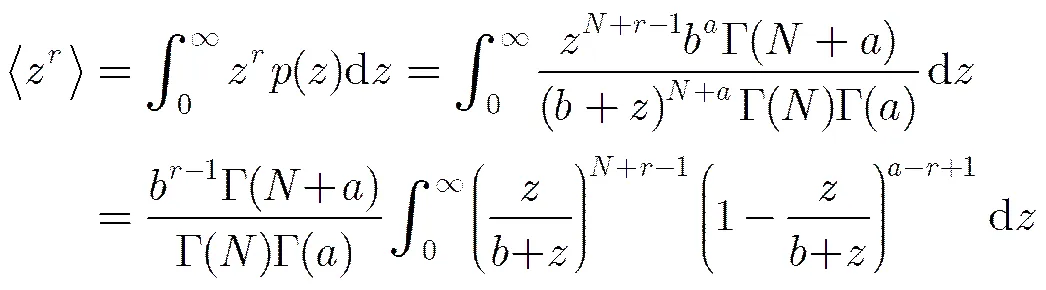
(8)

3.3 本文方法

(12)

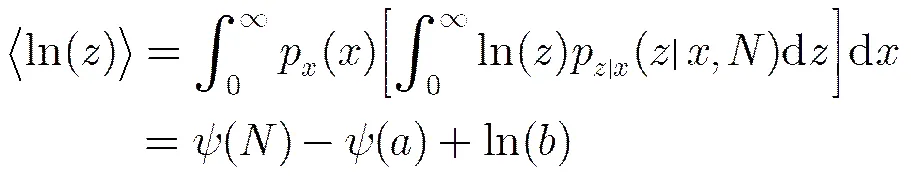
式(12)减式(13)，得

(14)

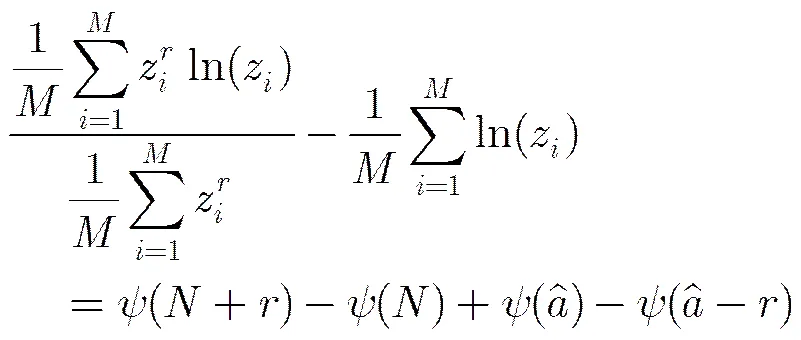
(16)

4 估计精度分析

分析参数的估计精度需要产生具体已知参数的Pareto分布随机数作为样本。产生形状参数为、尺度参数为的Pareto分布数据(为的矩阵)的步骤为：

为了进一步分析本文方法的参数估计性能，图5，图6同时给出时的方法、方法与一二阶矩法的参数相对估计偏差与相对估计方差。从图中可以看到，在区间法的相对估计偏差与相对估计方差均远远小于法与一二阶矩法。甚至在时的相当一部分区域，法的估计性能也优于法与一二阶矩法。

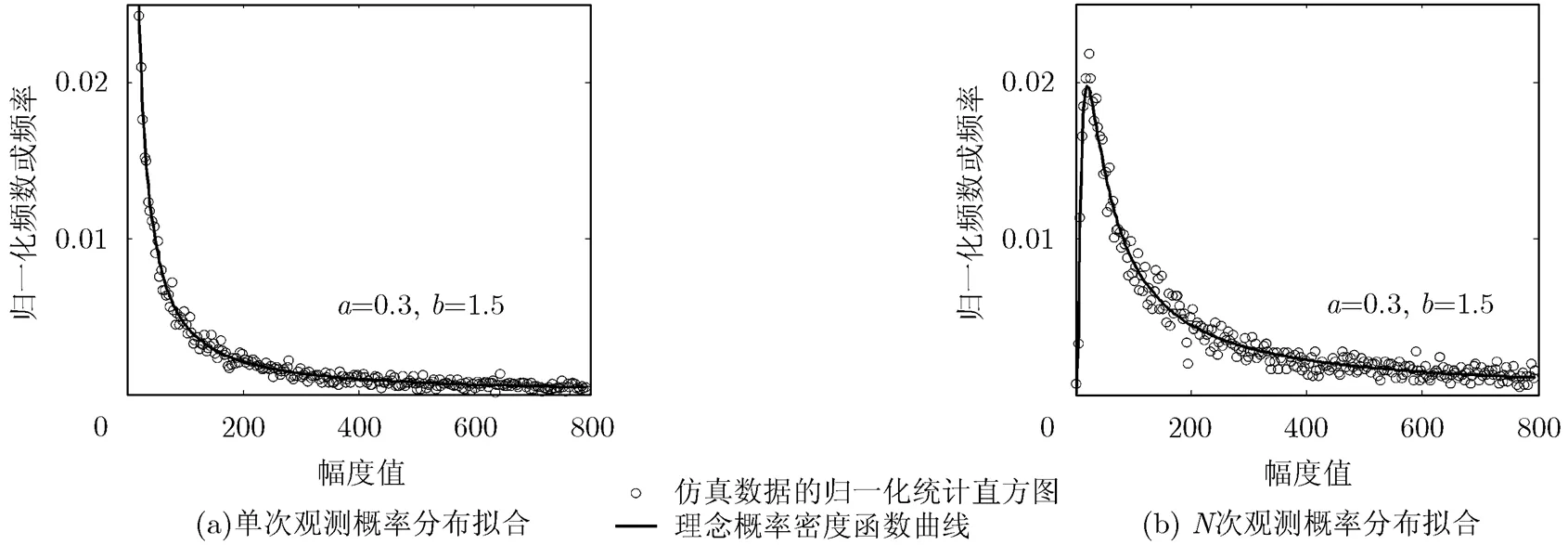
图1 仿真数据统计分布

图2 估计值-真值曲线         图3 估计结果相对偏差        图4 估计结果相对方差

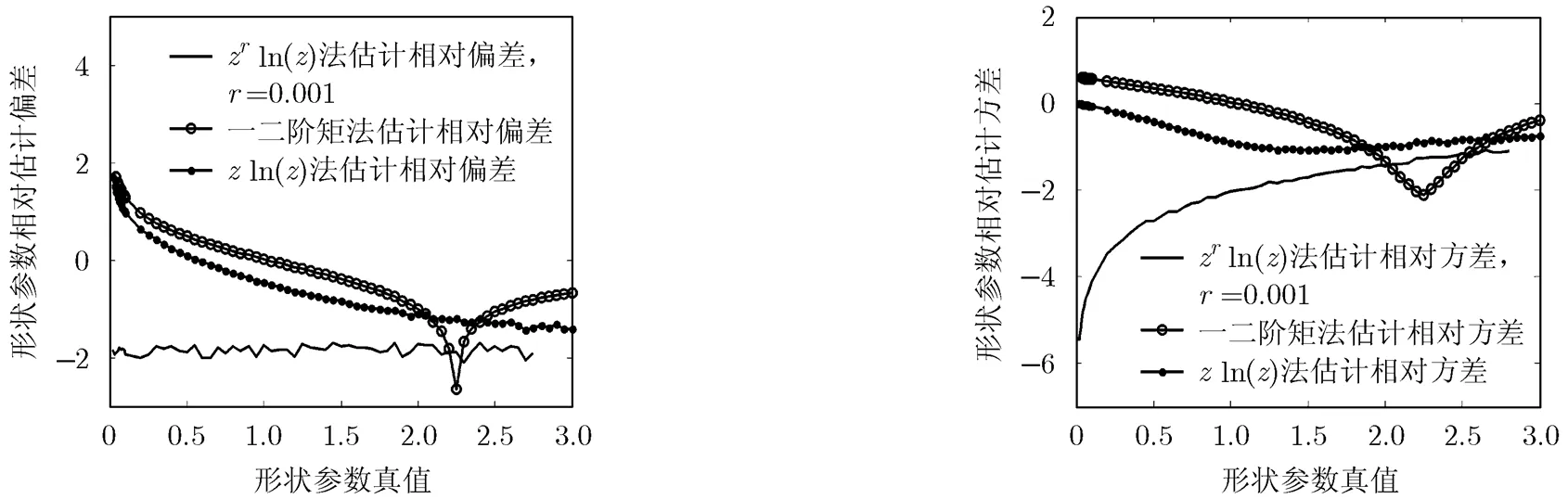
图5 3种不同估计器的相对估计偏差        图6 3种不同估计器的估计方差

5 结束语

基于一二阶矩的次观测Pareto分布参数估计方法不能有效估计小于2的形状参数，基于的估计方法不能有效估计小于1的形状参数。本文所使用的基于的方法扩大了形状参数的有效估计范围，可以有效估计区间上的形状参数。仿真实验表明，法不但在区间的参数估计性能远胜于一二阶矩法与法，而且在的一些区域，参数估计性能也优于一二阶矩法与方法的估计性能，因此该方法大大拓宽了次观测Pareto分布参数估计范围。

[1] 丁鹭飞, 耿富录, 陈建春, 等. 雷达原理[M]. 第四版, 北京: 电子工业出版社, 2009: 230-233.

DING Lufei, GENG Fulu, CHEN Jianchun,. Radar Theory[M]. 4th Edition, Beijing: Publishing House of Electronics Industry, 2009: 230-233.

[2] WEINBERG G V. Assessing Pareto fit to high-resolution high-grazing-angle sea clutter[J]., 2011, 47(8): 516-517. doi: 10.1049/el.2011.0518.

[3] BOCQUET S and ROSENBERG L. Simulation of coherent sea clutter with inverse gamma texture[C]. International Radar Conference, Lille, 2014: 1-6. doi: 10.1109/RADAR. 2014.7060347.

[4] 张玉石, 许心瑜, 尹雅磊, 等. L波段小擦地角海杂波幅度统计特性研究[J]. 电子与信息学报, 2014, 36(5): 1044-1048. doi: 10.3724/SP.J.1146.2013.01139.

ZHANG Yushi, XU Xinyu, YIN Yalei,. Research on amplitude statistics of L-band low grazing angle sea clutter[J].&, 2014, 36(5): 1044-1048. doi: 10.3724/SP.J.1146.2013.01139.

[5] WANG J N and XU X J. Simulation of correlated low- grazing-angle sea clutter based on phase retrieval[J]., 2015, 53(7): 3917-3930. doi: 10.1109/TGRS.2014.2388211.

[6] WANG J N and XU X J. Simulation of Pareto distributed temporally and spatially correlated low grazing angle sea clutter[C]. International Radar Conference, Lille, 2014: 1-6. doi: 10.1109/RADAR.2014.7060342.

[7] WEINBERG G V. Validity of whitening-matched filter approximation to the Pareto coherent detector[J]., 2012, 6(6): 546-550. doi: 10.1049/iet-spr.2011. 0304.

[8] FARSHCHIAN M and POSNER F L. The Pareto distribution for low grazing angle and high resolution X-band sea clutter[C]. IEEE Radar Conference, Washington DC, 2010: 271-285. doi: 10.1109/RADAR.2010.5494513.

[9] ALEXOPOULOS A and WEINBERG G V. Fractional order Pareto distributions with application to X-band maritime radar clutter[J].,&, 2015, 9(7): 817-826. doi: 10.1049/iet-rsn.2014.0379.

[10] ROSENBERG L and BOCQUET S. The Pareto distribution for high grazing angle sea-clutter[C]. IEEE International Geoscience and Remote Sensing Symposium, Melbourne, 2013: 4209-4212. doi: 10.1109/IGARSS.2013.6723762.

[11] SANGSTON K J, GINI F, and GRECO M S. New results on coherent radar target detection in heavy-tailed compound-Gaussian clutter[C]. IEEE Radar Conference, Washington DC, 2010: 779-784. doi: 10.1109/RADAR.2010. 5494515.

[12] BALLERI A, NEHORAI A, and WANG J. Maximum likelihood estimation for compound-Gaussian clutter with inverse-gamma texture[J]., 2007, 43(2): 775-780. doi: 10.1109/ TAES.2007.4285370.

[13] MEZACHE A, IZZEDDINE C, SOLTANI F,. Estimating the Pareto plus noise distribution parameters using non-integer order moments and [log()] approaches[J].,&, 2016, 10(1): 192-204. doi: 10.1049/iet-rsn.2015.0170.

[14] BOCQUET S. Simulation of correlated Pareto distributed sea clutter[C]. International Conference on Radar, Adelaide, 2013: 258-261. doi: 10.1109/RADAR.2013.6651995.

HU Wenlin, WANG Yongliang, and WANG Shouyong. Estimation of the parameters of K-distribution based onexpectation[J].&, 2008, 30(1): 203-205. doi: 10.3724/SP.J.1146. 2006.00829.

Widening Efficacious Parameter Estimation Range of Multi-look Pareto Distribution

HU Chong LUO Feng ZHANG Linrang FAN Yifei CHEN Shuailin

(,,710071,)

The method for estimating the parameters of multi-look Pareto distribution based oncan not estimate the shape parameter less than 1. To overcome the drawback, it is generalized by, which widens the efficacious range for shape parameter to be estimated. The expression of parameter estimation is deduced so as to demonstrate that the proposed method is able to estimate the shape parameter less than 1 theoretically. The simulation results validate that the method ofis able to estimate the shape parameter more efficaciously in the range of.

Parameter estimation; Radar clutter; Pareto distribution; Multi-look

TN957.51

A

1009-5896(2017)02-0412-05

10.11999/JEIT160307

2016-04-01；改回日期：2016-09-01；

2016-10-17

罗丰 luofeng@xidian.edu.cn

国家重大科学仪器设备开发专项(2013YQ20060705)

The National Major Scientific Instruments and Equipment Development Program(2013YQ20060705)

胡 冲： 男，1987年生，博士生，研究方向为海杂波特性分析与建模、海杂波背景下的目标检测等.

罗 丰： 男，1971年生，教授，研究方向为雷达信号与信息处理、海杂波特性分析与建模、杂波背景下的目标检测、跟踪与航迹关联等.

张林让： 男，1966年生，教授，研究方向为阵列天线技术、组网雷达抗干扰、高超声速SAR成像技术等.

范一飞： 男，1989年生，博士生，研究方向为海杂波特性分析与建模、海杂波背景下的目标检测等.

陈帅霖： 男，1986年生，博士生，研究方向为杂波背景下的目标检测及跟踪及航迹关联等.