基于贝叶斯准则的随机共振算法研究

刘书君 杨 婷 唐明春 王 品 李勇明



基于贝叶斯准则的随机共振算法研究

刘书君*杨 婷 唐明春 王 品 李勇明

(重庆大学通信工程学院 重庆 400044)

该文针对二元假设检验问题，首先在贝叶斯准则的基础上，分析了最小化贝叶斯代价所对应的最优噪声，将贝叶斯代价的最小化问题等价为虚警概率和/或检测概率的最优化。其次，在保证一定虚警概率和检测概率的前提下，建立起能同时改善检测概率和虚警概率的模型。然后分别给出当检测概率一定时虚警概率最小和虚警概率一定时检测概率最大这两种极限情况下对应的最优加性噪声，并对其进行线性凸组合以获得模型所需的最优加性噪声，进一步分析并证明了该模型能够成立的充分条件。再次，获得先验概率已知和未知两种情况下最小化贝叶斯代价时所对应的加性噪声，且当先验知识发生改变时，该算法只需调整加性噪声中一个可变参数即可获得相应的最优贝叶斯代价。最后，结合具体的检测问题，通过仿真验证了所提算法的有效性。

信号处理；贝叶斯准则；噪声增强模型；加性噪声；假设检验

1 引言

噪声无处不在，理解和掌握噪声的分布和性能是一个非常重要的问题。在经典信号处理中，噪声被视为不需要的信号或是对系统的干扰[1]。例如，系统中噪声越多信道容量越小，使得检测性能和估计精度都有所下降。然而，噪声对系统的影响并不都是负面的。自20世纪80年代文献[2]首次提出随机共振的概念以来，噪声的积极作用被用于物理、化学、磁学、和电子学等许多领域的研究中。文献[11]将随机共振应用到双基地逆合成孔径雷达成像系统中，有效地提高了输出信噪比，使得雷达接收机的动态范围扩大，对目标精细特征探测和识别的能力提升。

随机共振在信号处理中所发挥的重要作用也逐渐引起人们的广泛关注，其本质是指噪声在一定条件下，通过非线性系统对信号和系统起到积极的增强作用，也被称为噪声增强现象[3]。近几年的研究表明，在信号检测理论中也存在随机共振现象。给一些系统的输入加入噪声或增加系统的背景噪声水平，可明显提高系统输出的性能。如文献[13]引入匹配噪声，通过匹配非线性系统、噪声和信号三者的关系，从而改变能量检测统计量的分布，有效地检测信号的存在性。在假设检测问题的随机共振理论中，通常采用信噪比[11]、互信息量[12]、检测概率[13,15]的提高，或者平均错误率[14]的降低作为衡量性能改善的标准，并根据奈曼皮尔逊准则[15]、贝叶斯准则[16]以及极大极小准则[17]来分析如何通过加入噪声来提高非最优检测器的性能。如文献[15]分析了在虚警概率一定的情况下，给观察值加入独立噪声使得检测概率最大化的问题，并推导出对应的最优噪声概率密度函数及检测概率能否提高的充分条件；文献[16]研究了在严格贝叶斯准则框架下噪声增强多元复合假设检验问题，其中贝叶斯准则和极大极小准则[17]下的随机共振优化问题可看作严格贝叶斯框架下的特例。

在以贝叶斯代价最小准则添加噪声的相关文献中，研究者通常把贝叶斯代价作为一个整体来估计其最优化时对应的加性噪声，虽然可以优化贝叶斯代价，但并不能保证检测器的虚警概率和检测概率同时得到改善，甚至可能使得其中之一的性能降低。同时，当先验概率或者条件代价发生变化时，需要重新估计新参数下最优贝叶斯代价所需的加性噪声，增加了计算的复杂度。本文在研究贝叶斯准则下如何添加加性噪声的问题时，将贝叶斯代价的优化转化为虚警概率和检测概率的优化问题。因此，本文在保证一定虚警概率和检测概率的前提下，首先提出了一种基于贝叶斯准则的随机共振模型，并利用当检测概率一定时，虚警概率取最小值时对应的最优加性噪声，以及虚警概率一定时，最大化检测概率所对应的加性噪声这两种极限情况下的最优噪声的线性组合获得最小化贝叶斯代价的合适的噪声。然后，详细推导了这两种极限情况所对应的最优噪声。其次，给出了该模型能够成立的加性噪声以及充分条件。再次，给出了先验概率已知和未知时，分别对应的最小化贝叶斯代价的加性噪声。本文算法的优势在于当改变先验概率和条件代价时，只需调节最优加性噪声模型中的参数值即可获得最小化贝叶斯代价对应的加性噪声，在保证性能的同时简化了运算。最后，结合具体的检测问题对不同情况下对应的最优噪声进行求解，并通过仿真分析了在不同情况下添加噪声时对检测性能的影响，证明了本文算法的有效性和正确性。

2 最优贝叶斯代价的随机共振算法

2.1 基于贝叶斯准则的随机共振

考虑如式(1)中的二元假设检验问题：

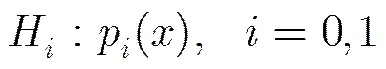
(2)

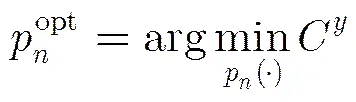
(4)

(6)

其中，

(8)

(10)

2.2 最优贝叶斯代价的随机共振模型

(13)

3 综合性能改善下的最优加性噪声

为了获得如式(13)所示情况(3)对应的加性噪声概率密度函数，以下分别对两种极限情况下的性能改善程度与相应最优噪声概率密度函数进行详细分析，并给出可同时改善虚警概率和检测概率的充分条件。

(16)

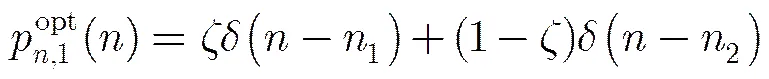
由文献[15]可知，极限情况(2)下的最优噪声概率密度函数和加噪后的检测概率及其改善程度表示为

(19)

在获得如式(17)和式(20)所示的两种极限情况下对应的最优噪声后，将其代入式(13)，并根据具体应用需求选择适合的参数即可获得能同时改善检测概率与虚警概率的适合的加性噪声概率密度函数。此外，当或时，可直接得出式(13)模型所定义的情况(3)中适合的加性噪声可为概率密度函数为的直流信号。当时，由和确定；当时，由和确定。

3.3 检测概率和虚警概率同时改善的充分条件

以上4个条件中任意一个成立时，至少存在一个概率密度函数为的噪声使得和同时成立。

4 贝叶斯准则下最优加性噪声

将式(13)代入式(10)得

(23)

式(22)与式(23)中最小值的求解分别对应了极限情况(1)和情况(2)的求解。在文献[17]中，求的最小化的问题是一个非线性的过程，对应最优加性噪声设为，因为为已知常量则最终是作用在或者上的。在和的情况下，通过对和的求解可知，,分别为令,取得最优值的加性噪声，则有,。因此，在此情况下，本文算法优于文献[17]中的结果。

5 实验与仿真分析

本节将针对不同的背景噪声分布下已知常量的检测问题，结合仿真分析对前文的结论进行验证。考虑如下二元假设检验例子。

(25)

5.1 高斯分布背景噪声

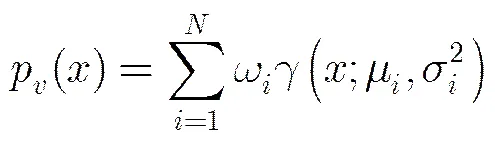
(27)

(29)

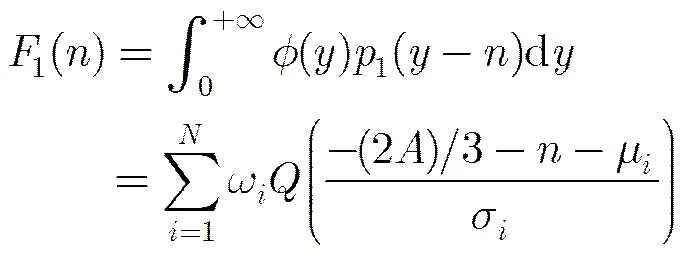
图1与的关系示意图

5.2 瑞利分布背景噪声

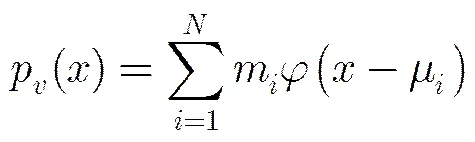
(32)

图3 不同瑞利背景噪声方差下的检测性能

6 结论

本文基于贝叶斯准则，分析了在贝叶斯准则下，加入噪声使得贝叶斯代价最小化问题等价于使得虚警概率和/或检测概率最优化的问题。本文在保证和的情况下，提出了同时使得虚警概率降低和检测概率提高的加性噪声增强检测模型。然后给出了3种不同情况下对应的最优加性噪声及模型能够成立的充分条件。再次，给出了先验概率已知和未知时，分别对应的最小化贝叶斯代价的加性噪声，并且在改变先验概率和条件代价时，只需调节最优噪声模型中的参数值即可获得相应的加性噪声，在保证性能的同时简化了运算。检测实例和仿真结果分析均证明了本文算法的有效性。

[1] COHEN L. The history of noise[J]., 2005, 22(6): 20-45. doi: 10.1109/MSP.2005. 1550188.

[2] BENZI R, SUTERA A, and VULPIANI A. The mechanism of stochastic resonance[J].:, 1981, 14(11): L453-L457. doi: 10.1088 /0305-4470/14/11/006.

[3] 张雷, 宋爱国. 随机共振在信号处理中应用研究的回顾与展望[J]. 电子学报, 2009, 37(4): 811-818. doi: 10.3321/j.issn: 0372-2112.2009.04.025.

ZHANG Lei and SONG Aiguo. Development and prospect of stochastic resonance in signal processing[J]., 2009, 37(4): 811-818. doi: 10.3321/j.issn:0372-2112. 2009.04.025.

[4] ADDESSOA P, PIERROB V, and FILATRELLA G. Interplay between detection strategies and stochastic resonance properties[J].&, 2015, 30(1/3): 15-31. doi: 10.1016/j.cnsns.2015.05.026.

[5] YU Haitao, GUO Xinmeng, WANG Jiang,. Adaptive stochastic resonance inself-organized small-world neuronal networks with time delay[J].&, 2015, 29(1/3): 346-358. doi: 10.1016/j.cnsns.2015.05.017.

[6] 张海滨, 何清波, 孔凡让. 基于变参数随机共振和归一化变换的时变信号检测与恢复[J]. 电子与信息学报, 2015, 37(9): 2124-2131. doi: 10.11999/JEIT141618.

ZHANG Haibin, HE Qingbo, and KONG Fanrang. Time-varying signal detection and recovery method based on varying parameter stochastic resonance and normalization transformation[J].&, 2015, 37(9): 2124-2131. doi: 10.11999/ JEIT141618.

[7] 侯成郭, 罗柏文, 李地. 线性调频信号的级联随机共振数字化接收[J]. 电子与信息学报, 2015, 37(12): 2866-2871. doi: 10.11999/JEIT141496.

HOU Chengguo, LUO Bowen, and Li Di. Cascaded stochastic resonance for digitized receiving of linear frequency modulation signal[J].&, 2015, 37(12): 2866-2871. doi: 10.11999/ JEIT141496.

[8] CHEN Hao, VARSHNEY L R, and VARSHNEY P K. Noise-enhanced information systems[J]., 2014, 102(10): 1607-1621. doi: 10.1109/JPROC.2014. 2341554.

[9] LIU Shujun, YANG Ting, and ZHANG Xinzheng. Effects of stochastic resonance for linear–quadratic detector[J].,&, 2015, 77(1): 319-331. doi: 10.1016/j. chaos.2015.06.015.

[10] LU Zeqi, CHEN Liqun, MICHAEL J B,Stochastic resonance in a nonlinear mechanical vibration isolation system[J].&, 2016, 370: 221-229. doi: 10.1016/j.jsv.2016.01.042.

[11] 邓冬虎, 朱小鹏, 张群, 等. 基于随机共振理论的双基ISAR 弱信号提取及成像分析[J]. 电子学报, 2012, 40(9): 1809-1816. doi: 10.3969/j.issn.0372-2112.2012.09.017.

DENG Donghu, ZHU Xiaopeng, ZHANG Qun,Weak signals extraction and imaging analysis in bistatic ISAR systems based on stochastic resonance[J]., 2012, 40(9): 1809-1816. doi: 10.3969/j.issn.0372-2112. 2012.09.017.

[12] MITAIM S and KOSKO B. Adaptive stochastic resonance in noisy neurons based on mutual information[J]., 2004, 15(6): 1526-1540. doi: 10.1109/TNN.2004.826218.

[13] 高锐, 李赞, 吴利平, 等. 低信噪比条件下基于随机共振的感知方法与性能分析[J]. 电子学报, 2013, 41(9): 1672-1679. doi: 10.3969/j.issn.0372-2112.2013.09.002.

GAO Rui, LI Zan, WU Liping,. A spectrum sensing method and performance analysis based on stochastic resonance under low SNR[J]., 2013, 41(9): 1672-1679. doi: 10.3969/j.issn.0372-2112.2013.09.002.

[14] KAY S M, MICHELS J H, CHEN Hao,Reducing probability of decision error using stochastic resonance[J]., 2009, 13(11): 695-698. doi: 10.1109/LSP.2006.879455.

[15] CHEN Hao, VARSHNEY P K, KAY S M,. Theory of the stochastic resonance effect in signal detection: Part IFixed detectors[J]., 2007, 55(7): 3172-3184. doi: 10.1109/TSP.2007.893757.

[16] BAYRAM S, GEZICI S, and VINCENT P H. Noise enhanced hypothesis-testing in the restricted Bayesian framework[J]., 2010, 58(8): 3972-3989. doi: 10.1109/TSP.2010.2048107.

[17] BAYRAM S and GEZICI S. Noise enhanced M-ary hypothesis-testing in the Minimax framework[C]. The 3rd International Conference on Signal Processing Communication Systems (ICSPCS), Omaha, NE, USA, 2009: 1–6. doi: 10.1109/ICSPCS.2009.5306400.

[18] 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 北京: 高等教育出版社, 2010: 76–77.

SHENG Zhou, XIE Shiqian, and PAN Chengyi. Probability and Statistics[M]. Beijing: Higher Education Press, 2010: 76–77.

Study on Stochastic Resonance Algorithm Based on Bayes Criterion

LIU Shujun YANG Ting TANG Mingchun WANG Pin LI Yongming

(,,400044,)

The optimal noise that minimizes Bayes risk for a binary hypothesis testing problem is analyzed firstly. As a result, the minimization of Bayes risk can be equivalent as the optimization of the detection probabilityand/or false alarm probability. Secondly, a noise enhanced model, which can increaseand decreasesimultaneously, is established under the premise of maintaining predefinedand. Then the optimal additional noise of this model is obtained by a convex combination of two optimal noises of two limit cases, which are the minimization ofwith maintaining the predefinedand the maximization ofwith maintaining the predefined, respectively. Furthermore, the sufficient conditions for this model are given. What’s more, the additive noise that minimizes the Bayes risk is determined when the prior probabilities are known or not, and the corresponding additive noise can be obtained by recalculating a parameter only if the prior information changes. Finally, the availability of algorithm is proved through the simulation combined with a specific detection example.

Signal processing; Bayes criterion; Noise enhanced model; Additive noise; Hypothesis testing

TN911.7

A

1009-5896(2017)02-0293-08

10.11999/JEIT160361

2016-04-14；改回日期：2016-10-18；

2016-12-20

刘书君 liusj@cqu.edu.cn

重庆市基础与前沿研究(cstc2016jcyjA0134, cstc2016 jcyjA0043)，国家自然科学基金(61501072, 61301224, 41404027, 61108086, 61471072)，重庆市社会事业与民生保障专项(cstc2016 shmszx40002)，中央高校重点基金(CDJZR155507)

The Basic and Advanced Research Project in Chongqing (cstc2016jcyjA0134, cstc2016jcyjA0043), The National Natural Science Foundation of China (61501072, 61301224, 41404027, 61108086, 61471072), The Chongqing Social Undertaking and People,s Livelihood Guarantee Science and Technology Innovation Special Foundation (cstc2016shmszx40002), The Fundamental Research Funds for the Central Universities (CDJZR155507)

刘书君： 女，1981年生，讲师，研究方向为统计信号分析、图像处理.

杨 婷： 女，1990年生，博士生，研究方向为噪声增强信号处理、统计信号分析.

唐明春： 男，1981年生，研究员，研究方向为天线与电波传播、微波毫米波理论与技术.

王 品： 女，1979年生，副教授，研究方向为智能信息处理、光学信息处理.

李勇明： 男，1976年生，副教授，研究方向为智能计算与模式识别、数据挖掘.