基于分裂基-2/(2a)FFT算法的卷积神经网络加速性能的研究

伍家松 达 臻 魏黎明 SENHADJI Lotfi 舒华忠



基于分裂基-2/(2)FFT算法的卷积神经网络加速性能的研究

伍家松*①②④达 臻①④魏黎明①④SENHADJI Lotfi②③④舒华忠①②④

①(东南大学计算机网络和信息集成教育部重点实验室 南京 210096)②(法国国家医学与健康研究院 U1099 雷恩 35000)③(雷恩一大信号与图像处理实验室 雷恩 35000)④(中法生物医学信息研究中心 南京 210096)

卷积神经网络在语音识别和图像识别等众多领域取得了突破性进展，限制其大规模应用的很重要的一个因素就是其计算复杂度，尤其是其中空域线性卷积的计算。利用卷积定理在频域中实现空域线性卷积被认为是一种非常有效的实现方式，该文首先提出一种统一的基于时域抽取方法的分裂基-2/(2) 1维FFT快速算法，其中为任意自然数，然后在CPU环境下对提出的FFT算法在一类卷积神经网络中的加速性能进行了比较研究。在MNIST手写数字数据库以及Cifar-10对象识别数据集上的实验表明：利用分裂基-2/4 FFT算法和基-2 FFT算法实现的卷积神经网络相比于空域直接实现的卷积神经网络，精度并不会有损失，并且分裂基-2/4能取得最好的提速效果，在以上两个数据集上分别提速38.56%和72.01%。因此，在频域中实现卷积神经网络的线性卷积操作是一种十分有效的实现方式。

信号处理；深度学习；卷积神经网络；快速傅里叶变换

1 引言

深度学习是加拿大多伦多大学Hinton教授等人[1,2]于2006年提出的一种新的机器学习方式，其将无监督的逐层初始化(Layer-wise Pretraining)结构和深度神经网络(Deep Neural Networks, DNN)结构进行了有效的结合。深度学习被《麻省理工技术评论》杂志评选为2013年世界十大技术突破之一，吸引了学术界和工业界的广泛关注，在语音识别和图像识别等众多领域取得了突破性进展。卷积神经网络因为建模难度适中且性能优异，逐渐成为深度学习中众多学习结构中被广泛采纳的一种结构。限制卷积神经网络大规模应用的很重要的一个因素就是其计算复杂度，尤其是其中线性卷积的计算。Jaderberg等人[9]提出用低秩矩阵分解的方法来加速线性卷积的计算。Liu等人[10]提出同时结合低秩矩阵分解和稀疏约束的方法来加速线性卷积的计算。Vasilache等人[11]则提出在GPU环境下运用最简单的基-2 FFT[12]算法来加速线性卷积的实现。但是正如Liu等人[10]指出的虽然目前大型的卷积网络系统大部分是在GPU环境下实现，但是在普通的CPU环境中仍然有其自身的通用性的优势：基于CPU的系统能够方便地部署在目前通用的商品化集群系统(commodity clusters)中，而不需要任何特殊的GPU结点。因此研究CPU环境下卷积神经网络的构造也是一件十分有意义的研究工作。

虽然在卷积神经网络框架下利用快速傅里叶变换(Fast Fourier Transform, FFT)算法进行线性卷积加速的研究工作还很少[11]，但是，CPU环境下通用FFT快速算法的深入研究则一直吸引着研究人员广泛的关注。目前FFT算法最具代表性的主要有3类[13]：(1)Winograd傅里叶变换算法(Winograd Fourier Transform Algorithm, WFTA)[14]。WFTA只能处理长度为且和为互质数的傅里叶变换[13]。WFTA在3类算法中需要的乘法复杂度最低，加法复杂度最高，并且实现起来最为复杂。WFTA只适用于当数据的传输代价相比与浮点数运算代价可以忽略的情况[13]，然而对于现代计算机来说，传输速度仍然比浮点数计算的速度要慢。(2)素因子算法(Prime Factor Algorithm, PFA)[15]。PFA同样只能处理长度为且和为互质数的傅里叶变换[13]。PFA比WFTA需要更多的乘法，但是需要更少的加法，并且比WFTA更容易实现。(3)Cooley-Tukey类型的FFT算法[12]。比如：Cooley与Tukey[12]提出了著名的基-2 FFT算法，具有非常规则的实现结构。Duhamel 等人[16]提出了计算复杂度更低的分裂基-2/4 FFT算法。Bouguezel等人[17]则提出了一种统一的基于频域抽取方法的分裂基-2/2FFT算法，其中为任意自然数。Bi等人[18]则更进一步提出一种统一的基于频域抽取方法的分裂基FFT快速算法，其中为任意自然数，该算法包含了其它分裂基算法[12,16,17]，并且比素因子算法具有更低的计算复杂度。分裂基算法拥有许多其它两类算法(WFTA, PFA)所无法比拟的优势[13]，比如：(1)非常适合于处理长度为的实数数据，其中为任意自然数；(2)取得了计算复杂度和实现复杂度之间很好的均衡；(3)适合于同址计算，能够有效地利用规则的蝶型结构进行计算，实现程序非常简洁和紧凑；(4)具有很好地抑制量化噪声的能力；(5)适合于并行实现。需要注意的是文献[16-18]的方法都是基于频域抽取的FFT算法。但是在有些应用场合，比如滑动窗FFT算法，为了与时域滑动过程相吻合，必须采用基于时域抽取的FFT算法。

本文主要研究不考虑GPU硬件加速的情况下，基于时域抽取的FFT算法在CPU环境下对卷积神经网络的加速性能。本文剩下的几个部分组织结构如下：第2节提出一种统一的基于时域抽取方法的分裂基1维FFT快速算法，并对其计算复杂度进行了分析；第3节利用经典的行列方法将提出的1维FFT算法推广到2维，并对得到的2维FFT算法的计算复杂度进行了分析，并且在卷积神经网络的框架下介绍了FFT算法的应用；第4节通过实验研究了基于时域抽取方法的分裂基FFT算法对卷积神经网络的加速性能。

2 1维分裂基-2/(2a)FFT算法及其复杂度分析

1维离散傅里叶变换(Discrete Fourier Transform, DFT)及其反变换分别定义为[22]

(2)

Bi等人[18]提出基于频域抽取的分裂基FFT算法，该算法将DFT的系数()拆分为偶数项(2)和奇数项(2+)，其中为任意自然数，为奇数变量并且。偶数项(2)的计算使用基-2 FFT的分解方式：

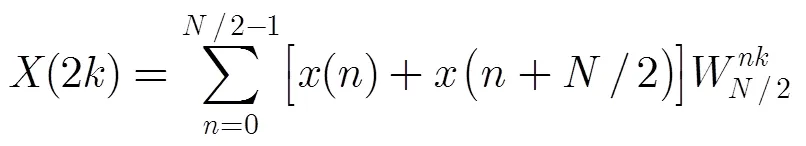
而奇数项(2+)则可以表达为

(4)

下面我们在Bi等人[18]提出的频域抽取分裂基FFT算法的基础上，提出一种新的时域抽取分裂基FFT算法。

式(1)可以通过式(5)的方法计算：

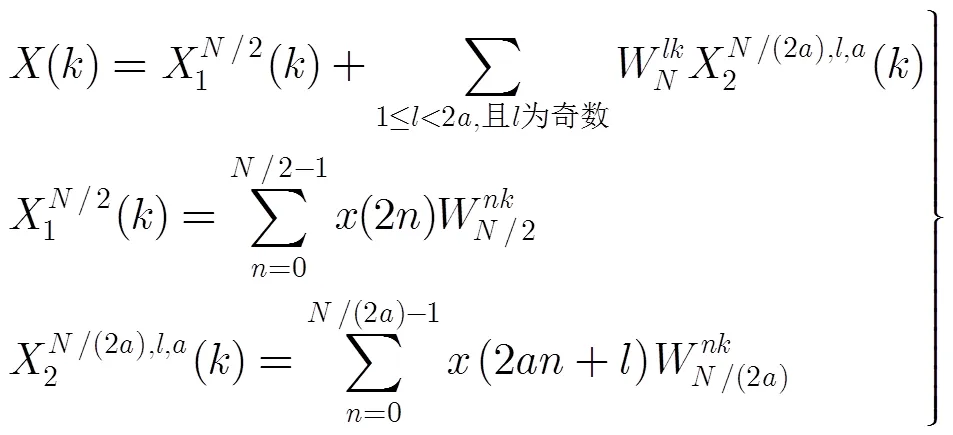
下面分析1维DFT正变换的计算复杂度。1次复数乘法相当于做4次实数乘法和2次实数加法。1次复数加法相当于做2次实数加法。分裂基FFT算法需要的理论上的乘法次数和加法次数如表1所示。

3 卷积神经网络与分裂基-2/(2a)FFT算法的结合

3.1 2维FFT算法应用于CNN中的计算复杂度分析

2维DFT[22]可以利用经典的行-列算法，通过1维DFT实现如式(7)所示。

由式(7)可知，2维DFT正变换可以通过先对列做2个长度1的1维DFT，再对行做1个长度2的1维DFT来实现。因此2维FFT算法需要的计算复杂度为1维FFT算法的(1+2)倍。

3.2 卷积神经网络框架下的FFT算法的应用

目前在卷积神经网络框架下利用FFT算法进行线性卷积的加速，通常优先选择自己开发其中的FFT算法模块(比如：已经取得成功的fbfft[11]算法)，而不是直接选择相对成熟的FFTW软件包[23]和FFTE软件包[24]。原因主要包括：(1)卷积神经网络框架下不但需要做线性卷积操作，还需要进行反向传播等操作，自己开发的FFT算法能够更好地与反向传播等操作相结合[11]；(2)在某些应用场合(比如：基于滑动窗的图像检测[25])，为了进一步加速线性卷积的计算需要用到滑动窗DFT算法[19,20]，通用的FFTW, FFTE软件包不容易与滑动DFT算法结合，此时，使用基于时域抽取的分裂基算法更容易与滑动DFT算法结合。

对于网络中给定的一层，令幅输入图像集合为{1,2,,,,}，其中表示第幅2维图像矩阵，大小为×；与该层相连的权值矩阵为，大小为×；该层的幅输出特征图像集合为{1,2,,,,}，其中表示第幅输出特征图像(output feature map)，大小为。

对于一般的反向传播算法[11](Back Propagation, BP)，在前向传播的过程中，需要对输入矩阵做卷积，即

(9)

表1 分裂基FFT算法计算复杂度分析(a=1,2)

表1 分裂基FFT算法计算复杂度分析(a=1,2)

FFT算法计算复杂度表达式初始值 基-2 分裂基-2/4

将FFT算法应用于以上过程可以得到以下两小节中的算法(注意：下面算法中每一层的输出隐含了激活函数的作用)。

3.2.1 前向计算算法

输入：某一层的某个输入矩阵，以及相应的权值矩阵。

输出：该层的输出特征值矩阵。

(1) 将权值矩阵“补零”到与输入矩阵相同的尺寸，这里假设,为自然数，使用分裂基FFT 正变换(式(7))将其变换到频域中，得到频域中的权值矩阵。

(2) 将输入矩阵同样进行分裂基FFT 正变换，得到频域中的输入矩阵。

(4) 对做分裂基FFT的反变换，并提取有效值区域，即可得到输出特征值矩阵。

3.2.2 反向求梯度算法

输出：每一个通道的损失函数关于偏置的梯度，损失函数关于本层权值矩阵(滤波器)的梯度，以及损失函数关于第层输出的梯度矩阵。

3.3 整个卷积神经网络在频域和空域中的计算复杂度近似分析

由于CNN的复杂性，想要精确计算整个卷积神经网络所需的加法次数和乘法次数是比较困难的。因此，这里使用所需的全部的运算次数这样一个稍微不精确的度量来衡量CNN的计算复杂性。众所周知，Cooley-Tukey FFT的复杂度总体来说都为(log2)，各种方法的差异仅在于一个常数，为方便起见，忽略这个常数。假设对于网络中的某一层来说，输入图像大小为×，卷积核的大小为×，输入图像的数量为，输出的特征图数量为，每个样例更新权值1次(即batchsize=)。在上述参数设置的情况下，空域直接线性卷积需要次运算，而运用FFT算法计算线性卷积则大约只需要次运算，这里忽略常数是合理的：因为分别在空域和在频域中做线性卷积时，两种方法的计算复杂度的数量级已经不同，忽略常数并不会对结果有太大的影响。

在空域中某一层迭代一次所需的运算次数为(包括前向传播和后向反馈的过程)[11]：

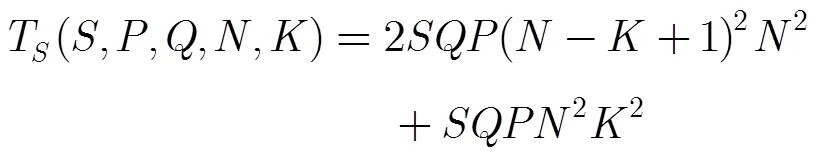
而在频域中某一层迭代一次所需的运算次数为

(12)

4 实验研究

实验的编程环境：Ubuntu 14.04 系统(64位)，Intel i7-4790K 4.00 GHz CPU和32 GB RAM，采用C++语言编程实现，使用g++编译器进行编译。未采用任何硬件加速手段(比如：GPU)。实验以FXT软件包[26]为基础进行编程。

4.1 1维分裂基-2/(2) FFT算法(=1,2)运行时间比较

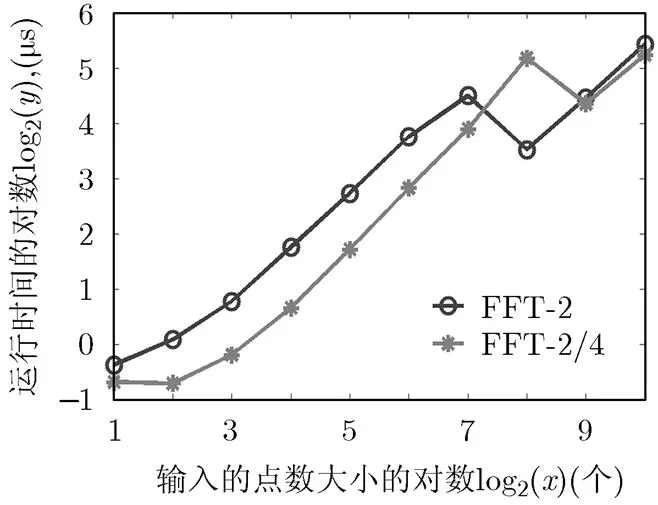
图1 1维分裂基-2/(2a) FFT算法(a=1,2) 实际耗费时间对比

4.2 2维基于分裂基-2/(2) FFT的行列算法运用于卷积神经网络性能的比较

4.2.1 MNIST手写数字分类数据集 MNIST手写数字数据集[27]一共有60000幅训练图像和10000幅测试图像。原始图像大小为28×28的灰度图像，为了有效地利用FFT算法，我们将原始图像周围补零成为32×32的灰度图像。

实验的主要目的并不是要比较识别正确率，所以实验中采用的是比较浅层的卷积神经网络结构。本实验采用5层的卷积神经网络，其结构如图2(a)所示。对于MNIST数据集大体结构如下：第1层为输入层；第2层为卷积层，在得到最终的卷积输出前还需要加上如图2(a)所示的偏置(由小圆圈表示)，第1层与第2层之间共有112个连接，选用大小为9×9的卷积核，每个卷积核在初始化时都不一样，当然在变换到频域乘积之前需要补零到与输入图像相同的大小；第3层为池化(Pooling)层，池化大小为6×6，采用最大池化方式；第2层与第3层之间采用一对一的连接方式，因此一共是112个连接；第4层是向量化层，即将第3层得到的小尺寸的特征图像例如4×4的图像，按照光栅扫描的顺序向量化为一个16×1的向量，将所有这样的小图像进行向量化并且连接在一起形成一个大尺寸的向量；最后一层是输出层，一共有10个神经元，这些神经元与第4层都是全连接的。

另外，隐含层即第2层卷积层使用了修正线性单元技术(ReLU)进行了校正，输出层使用softmax函数将结果归一化到0~1之间。误差准则采用的是交叉熵最小准则。训练使用反向传播算法，一共迭代10次，训练时间结果取平均值。这些都是在卷积神经网络中关于分类问题的典型做法。

首先，作为比较的标准，在第2个卷积层我们使用传统的空间域直接卷积的方法实现。训练使用反向传播算法，对于MNIST数据集，一共迭代10次，训练时间结果取平均值。其次，我们使用了上文所给出的两种2维分裂基FFT算法，实现图2(a)中的卷积过程。在整个训练测试过程中，程序运行良好，系统能够有效的识别输入的数据集。图2(b)给出了两种方式下CPU单线程运行训练过程所耗费的时间。而表2给出了原始图像经过补零成大小为32×32的输入图像后采用3种实现方式需要的训练时间以及训练集和测试集准确率，其中SC表示2维空域卷积，FC表示频域卷积，FC(FFT-2)表示使用基-2方法实现，FC(FFT- 2/4)表示使用分裂基-2/4方法实现。

从图2(b)可以看出，对于MNIST数据集，在频域中实现空域线性卷积的时间优势已经显现出来，使用基-2，分裂基-2/4的方式进行卷积的时间都比相应的空域中计算要少，这与理论分析的结果接近，同时，我们可以看到在频域实现中，使用分裂基-2/4方式的平均训练时间最短(1102.41 s)，相较于空域实现方法(1794.24 s)，速度提升38.56%。基-2算法平均耗时1636.45 s，相较于空域实现方法速度提升8.79%。

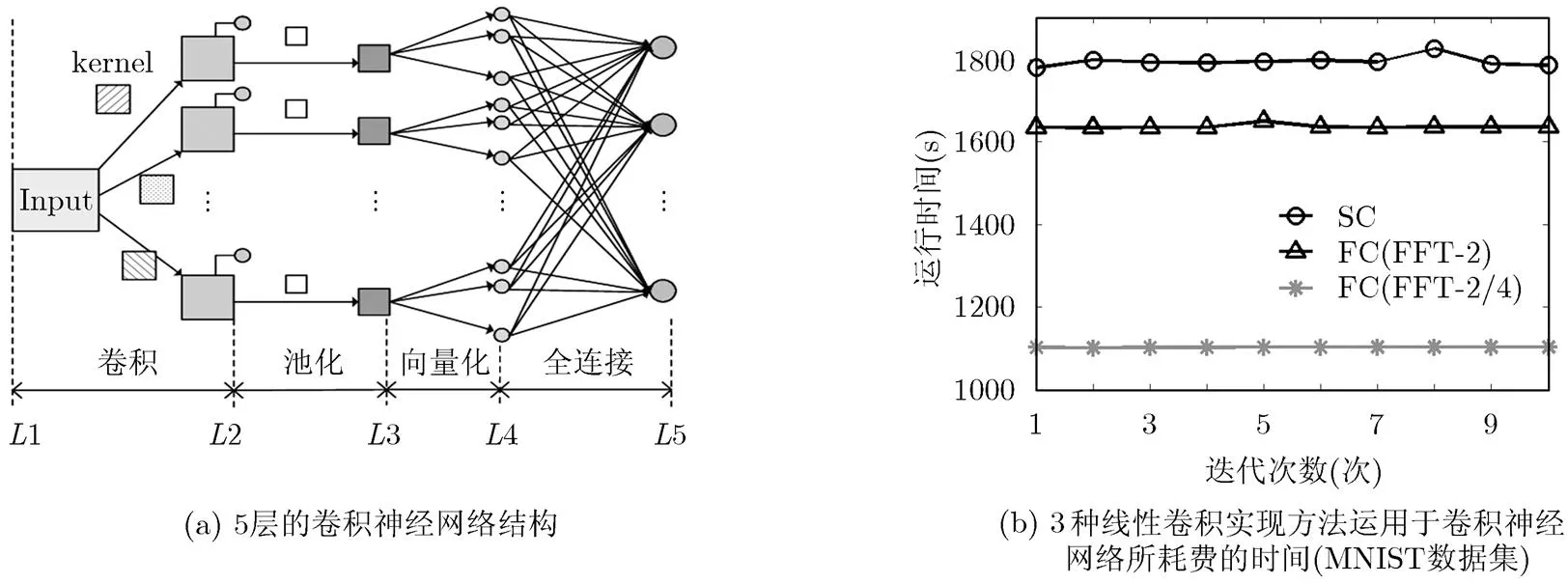
图2 实验采用的网络结构及实验结果

表2 3种卷积实现方式在卷积神经网络中的表现(MNIST)

4.2.2 Cifar-10对象识别数据集 Cifar-10数据集[28]一共有10类物体，每一类都有60000张图像(包括50000幅训练图像和10000幅测试图像)，每幅图像都是大小为32×32×3的三通道RGB彩色图像。同MNIST数据集的结果一样，使用分裂基-2/(2)的实验结果仍然比空域中直接进行线性卷积的结果要好，详细结果如表3所示。

在空域卷积实现方式下，每次迭代平均训练时间约为590 s，而使用基-2 FFT和分裂基-2/4 FFT实现方式的平均迭代时间分别降低为473 s和343 s，相较于空域实现的方式，两者分别提速24.73%和72.01%。迭代60次后，测试集的识别率没有显著差异，并且在每次的迭代过程中，也没有显著差异。

从表2以及表3中的每一次迭代结果对比来看，本文提出的基于分裂基-2/(2) FFT算法的卷积神经网络实现方式在实际中并不影响网络的训练精度和测试精度。理论上来说，除了在FFT变换时可能有的浮点数计算时的截断误差，其余的运算从结果上与CNN的空域卷积实现都是等价的。结合3.3节中的计算复杂度的分析，假设每一层的参数简化为，由式(24)和式(25)容易得到。目前流行的卷积神经网络以及个性化定制的网络结构仍有很多是基于“积木式”的堆叠，因此一般可以认为对于多个卷积层，其复杂度关系不变，于是该方式可以拓展到更深层的网络中。综合所有的结果来看，用分裂基-2/4的方式代替空域中的卷积会取得最好的提速效果。

从这些实验结果来看，在频域中实现卷积神经网络中的线性卷积操作，对于最后的分类结果并不会有显著的影响。对于大小为32×32的输入图像，在频域中实现的方法相较于空域直接实现的方法的时间优势已经显现出来。而且随着输入图像尺寸的增大，频域实现的计算时间比空域实现要更少，因为实现FFT只需要(log2)的计算复杂度，而计算空域线性卷积则需要的计算复杂度。因此在CPU环境下利用FFT在频域中实现卷积神经网络能比空域直接实现线性卷积神经网络具有更快的速度。

4.2.3 基于滑动窗卷积神经网络的图像检测的应用

通用的FFTW软件包[23]和FFTE软件包[24]虽然也可以用于卷积神经网络的加速，但是因为FFTW和FFTE软件包通常都采用了较为复杂的寻优策略，不容易在小幅度修改原有快速算法结构的情况下进一步加速卷积神经网络的实现，比如：基于滑动窗卷积神经网络的图像检测的应用[25]。本文提出的基于时域抽取的分裂基-2/(2)算法，因为采用的是一种简单的统一的快速算法结构，利用滑动窗DFT算法[19, 20]的策略只需要简单的注释掉输入模块中的部分代码，即可适用于滑动窗DFT算法的计算。

我们将在基于滑动窗卷积神经网络的图像匹配的应用场合中对比提出的基于时域抽取的分裂基-2/(2)算法与FFTW对于卷积神经网络的加速性能。使用MNIST数据库中的部分数据构成一幅图像，如图3所示。图像检测的任务是在这幅大小为320×320的大图像中检测出所有图像为数字“0”的小块，使用的卷积网络为4.2.1节中已经训练好的卷积神经网络。用一个大小为32×32的滑动窗分别遍历图3中图像的每一个像素，将得到的每一幅大小为32×32的图像输入图2所示的卷积神经网络。卷积的计算分别采用所提出的基于时域抽取的分裂基-2/4算法和FFTW算法[23]。图像检测的速度如表4所示。

表3 不同卷积方式在Cifar-10数据集上的迭代结果(后5次)

图3 MNIST数据库中的部分图像

表4 基于滑动窗卷积神经网络的图像检测速度比较(s)

由表4可以看出：在基于滑动窗卷积神经网络的图像检测的应用中，本文提出的基于时域抽取分裂基-2/4算法加速性能比FFTW速度提高大约8.7%。

5 结论

本文首先提出了一种统一的基于时域抽取方法的分裂基-2/(2)1维FFT快速算法，其中为任意自然数，然后通过行列算法将提出的1维FFT算法扩展到2维。在CPU环境下对提出的FFT算法在一种卷积神经网络中的加速性能进行了研究。在MNIST手写数字数据库以及Cifar-10对象分类中的实验结果表明：在不损失训练精度和测试精度的情况下利用分裂基-2/4 FFT算法和基-2 FFT算法实现的卷积神经网络比空域直接实现的卷积神经网络分别提速38.56%, 8.79%和72.01%, 24.73%。因此，在频域中实现卷积神经网络的线性卷积操作是一种十分有效的实现方式。

[1] HINTON G E and SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks[J], 2006, 313: 504-507.doi: 10.1126/science.1127647.

[2] HINTON G E, OSINDERO S, and TEH Y W. A fast learning algorithm for deep belief nets[J]., 2006, 18(7): 1527-1554. doi: 10.1162/neco.2006.18.7.1527.

[3] BENGIO Y, COURVILLE A, and VINCENT P. Representation learning: A review and new perspectives[J].,2013, 35(8): 1798-1828.doi: 10.1109/TPAMI. 2013.50.

[4] LECUN Y, BENGIO Y, and HINTON G E. Deep learning[J]., 2015, 521(7553): 436-444. doi: 10.1038/nature14539.

[5] DENG L and YU D. Deep learning: Methods and applications[J]., 2014, 7(3): 197-387.

[6] LECUN Y, BOTTOU L, BENGIO Y,. Gradient-based learning applied to document recognition[J]., 1998, 86(11): 2278-2324. doi: 10.1109/5.726791.

[7] KRIZHEVSKY A, SUTSKEVER I, and HINTON G E. Imagenet classification with deep convolutional neural networks[C]. Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 2012: 1097-1105.

[8] SZEGEDY C, LIU W, JIA Y Q,.. Going deeper with convolutions[C]. IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 2015: 1-9.

[9] JADERBERG M, VEDALDI A, and ZISSERMAN A. Speeding up convolutional neural networks with low rank expansions[J]., 2014, 4(4): XIII.

[10] LIU B, WANG M, FOROOSH H,. Sparse Convolutional neural networks[C]. IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, United States, 2015: 806-814.

[11] VASILACHE N, JOHNSON J, MATHIEU M,. Fast convolutional nets with fbfft: A GPU performance evaluation [C].International Conference on Learning Representations, San Diego, CA, USA, 2015: 1-17.

[12] COOLEY J W and TUKEY J W. An algorithm for the machine calculation of complex Fourier series[J].1965, 90(19): 297-301.doi: 10.2307/2003354.

[13] DUHAMEL P and VETTERLI M. Fast Fourier transforms: A tutorial review and a state of the art [J]., 1990, 19(4): 259-299. doi: 10.1016/0165-1684(90)90158-U.

[14] WINOGRAD S. On computing the discrete Fourier transform[J]., 1976, 73(4): 1005-1006. doi: 10.1073/pnas.73.4.1005.

[15] KOLBA D P and PARKS T W. A prime factor algorithm using high-speed convolution[J].&, 1977, 25(4): 281-294. doi: 10.1109/TASSP.1977.1162973.

[16] DUHAMEL P and HOLLMANN H. Implementation of Split-radix FFT algorithms for complex, real, and real symmetric data[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing, Tampa, FL, USA, 1985: 285-295.

[17] BOUGUEZEL S, AHMAD M O, and SWAMY M N S. A general class of split-radix FFT algorithms for the computation of the DFT of length-2[J].2007, 55(8): 4127-4138. doi: 10.1109/ TSP.2007.896110.

[18] BI G, LI G, and LI X. A unified expression for split-radix DFT algorithms[C]. IEEE International Conference on Communications, Circuits and Systems, Chengdu, China, 2010: 323-326.

[19] FARHANG BOROUJENY B and LIM Y C. A comment on the computational complexity of sliding FFT[J]., 1992, 39(12): 875-876. doi: 10.1109/82. 208583.

[20] PARK C S and KO S J. The hopping discrete Fourier transform[J]., 2014, 31(2): 135-139. doi: 10.1109/MSP.2013.2292891.

[21] GOUK H G and BLAKE A M. Fast sliding window classification with convolutional neural networks[C]. Proceedings of the 29th International Conference on Image and Vision Computing, New Zealand, 2014: 114-118.

[22] RAO K R, KIM D N, and HWANG J J. Fast Fourier Transform: Algorithms and Applications[M]. Berlin: Springer Science & Business Media, 2011: 5-6.

[23] FRIGO M and JOHNSON S G. FFTW: An adaptive software architecture for the FFT[C]. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Seattle, WA, USA, 1998: 1381-1384.

[24] TAKAHASHI D. FFTE: A fast fourier transform package [OL]. http://www.ffte.jp/, 2014.2.

[25] SERMANET P, EIGEN D, ZHANG X,Overfeat: Integrated recognition, localization and detection using convolutional networks[OL]. arXiv:1312.6229. 2013: 1-16.

[26] ARNDT J. Fxtbook[OL]. http://www.jjj.de/fxt/#fxtbook. 2015.1.

[27] LECUN Y, CORTES C, and CHRISTOPHER J C. The MNIST database of handwritten digits, Burges[OL]. http:// yann.lecun.com/exdb/mnist/, 2015.5.

[28] KRIZHEVSKY A, NAIR V, and HINTON G. Cifar-10 dataset[OL]. http://www.cs.toronto.edu/~kriz/cifar.html, 2009.1.

Acceleration Performance Study of Convolutional Neural Network Based on Split-radix-2/(2) FFT Algorithms

WU Jiasong①②④DA Zhen①④WEI Liming①④SENHADJI Lotfi②③④SHU Huazhong①②④

①((),,210096,)②(1099,35000,)③(’,1,35000,)④(-,210096,)

Convolution Neural Networks (CNN) make breakthrough progress in many areas recently, such as speech recognition and image recognition. A limiting factor for use of CNN in large-scale application is, until recently, their computational expense, especially the calculation of linear convolution in spatial domain. Convolution theorem provides a very effective way to implement a linear convolution in spatial domain by multiplication in frequency domain. This paper proposes an unified one-dimensional FFT algorithm based on decimation-in-time split- radix-2/(2), in whichis an arbitrary natural number. The acceleration performance of convolutional neural network is studied by using the proposed FFT algorithm on CPU environment. Experimental results on the MNIST database and Cifar-10 database show great improvement when compared to the direct linear convolution based CNN with no loss in accuracy, and the radix-2/4 FFT gets the best time savings of 38.56% and 72.01% respectively. Therefore, it is a very effective way to realize linear convolution operation in frequency domain.

Signal processing; Deep learning; Convolutional Neural Network (CNN); Fast Fourier Transform (FFT)

TN911.72

A

1009-5896(2017)02-0285-08

10.11999/JEIT160357

2016-04-12；改回日期：2016-12-02；

2016-12-29

伍家松 jswu@seu.edu.cn

国家自然科学基金(61201344, 61271312, 61401085)，高等学校博士学科点专项科研基金(20120092120036)

The National Natural Science Foundation of China (61201344, 61271312, 61401085),The Special Research Fund for the Doctoral Program of Higher Education (20120092120036)

伍家松： 男，1983年生，讲师，研究方向为卷积网络、离散正交变换快速算法.

达 臻： 男，1992年生，硕士生，研究方向为卷积网络.

魏黎明： 女，1993年生，硕士生，研究方向为卷积网络.

SENHADJI Lotfi： 男，1966年生，教授，研究方向为生物医学信号处理.

舒华忠： 男，1965年生，教授，研究方向为信号与图像处理.