串列双圆柱绕流问题数值模拟的多尺度分析

崔雪扬，曹博超，徐弘一

(复旦大学 航空航天系，上海 200433)

串列双圆柱绕流问题数值模拟的多尺度分析

崔雪扬，曹博超，徐弘一

(复旦大学 航空航天系，上海 200433)

运用有限体积法，对串列放置的双圆柱二维不可压缩流动进行了直接数值计算.在分析Strouhal数及升阻力系数等积分量的基础上，本文从流动多尺度层面研究了流场分布及涡结构.通过对速度场的流动显示和频谱分析，确定了涡脱落的多个频率，以及分别受上游圆柱和下游圆柱边界层扰动形成的多尺度涡的相互作用，并且发现由于多尺度涡的相互作用形成了更小尺度涡的过程及机理.最后，进一步将这些涡结构与流场模态对应起来，使得流场结构更加清晰地展现出来.

串列双圆柱； 直接数值模拟； 多尺度； 涡脱落； 脱落频率

流体绕流问题是工程中的常见问题，各种高大建筑物设计、飞行器设计、海洋石油平台及输油管道建设均涉及此类流动.此外，工业设备中也普遍存在绕流现象，如各类管壳式换热器等.因此研究钝体绕流的特性对工程实际和工业设备设计尤其重要，相关课题也一直是流体研究的热点.一个多世纪以来,圆柱绕流一直是众多理论分析、实验研究及数值模拟的对象，但迄今对该流动现象物理本质的理解仍未完整.

大多数实验研究的雷诺数高于104量级，而数值模拟大都在102量级进行.尽管计算中雷诺数远小于实际情况,但实验结果表明，伴随涡脱落的大尺寸尾流在一定程度上呈高、低雷诺数(102量级)相似的特征[1].因此,通过对低雷诺数问题的研究亦可基本反映高雷诺数流动的主要现象.虽然实际情形为3维流动，但2维问题的研究亦可反映该流动的一些主要特征.

在实验研究方面，Roshoko[2]最早在实验室中发现圆柱绕流存在与流场雷诺数相关的3个尾流状态；Zdravkovich[3]曾对两圆柱串列和交错放置的绕流问题进行过实验研究，针对两圆柱中心间距小于5倍圆柱直径的一系列情况，他研究了两圆柱间的流动相互作用，发现中心间距小于3倍圆柱直径时，没有明显的涡自上游圆柱脱落.

随着电子计算机的飞速发展，数值计算方面的研究也层出不穷，Phuocloc和Bouard[4]数值模拟绕流圆柱初期流动的2次涡结构，将得到的结果和实验比对，非常接近.邓见等[5]使用分块耦合方法，对单圆柱和串列双圆柱绕流进行了数值模拟，研究分析了双柱中心间距变化对上下游圆柱升阻力系数的影响，计算结果与试验结果非常吻合.廖俊等[6]使用表面涡法研究了高雷诺数下排列方式不同的双圆柱绕流，计算了圆柱在串列、并列以及错置情况下的各种流动结构、涡街变化及作用在圆柱上的力，所得的阻力系数与试验结果符合很好.

然而到目前为止，对圆柱绕流问题的研究大多集中在整体平均量层面，如同一雷诺数下探究阻力系数、升力系数和Strouhal数与间距直径比的关系，或者将数值模拟得到的流场信息，如流函数、涡量、涡脱落频率等与实验结果进行比较.随着科学研究的不断深入，对多尺度下流动规律的研究变得越来越重要.目前国内外对多尺度下低雷诺数圆柱绕流的研究还相对初步，有必要对低雷诺数下的圆柱绕流开展深入研究.

本文用有限体积法将非定常Navier-Stokes(N-S)方程进行离散，在求解域中采用直接数值模拟(Direct Numerical Simulation, DNS)方法计算得到流场信息，应用后处理软件Fieldview进行流场显示，根据流动结构和圆柱后涡脱落尾迹分布，取相关位置点进行流动的多尺度分析，以研究涡脱落频率、边界层扰流等流动基本特征，并结合模态和涡量图深入解析涡脱落机理.

1 数值计算方法

1.1控制方程及其差分离散格式

计算机的快速发展，使得DNS方法可在相对简单的流动几何构型中得以应用.但此方法要求网格点的数量多，计算量巨大.由于本文计算研究的是相对较低的雷诺数(Re=800)，使得DNS方法得以应用并得到较为精确的结果.

研究中的物理模型为2维不可压缩非定常流动的N-S方程：

式中：u，v是x，y方向的速度；μ为动力粘度；ρ为流体密度；t为计算总时长；p为作用在研究对象上的压力.

为获取具有普遍应用价值的流动数据，需要对方程进行无量纲化处理，所取特征物理量及相关无量纲物理量如下：

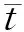
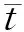
无量纲化后的2维不可压缩非定常流动的N-S方程可改写为：

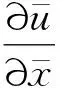
在对动量方程的离散中，对流项和扩撒项采用空间2阶中心格式.在时间方向，采用2阶精度的时间推进，对流项为2阶Adams-Bashforth显示格式，扩散项则采用2阶Adams-Moulton隐式格式.则离散方程可写为：

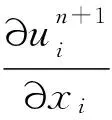
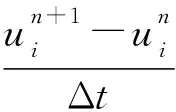
空间离散网格采用交错网格布局，如图1(见第386页)所示，即速度分量(u，v)和压力p各占据一套网格，这样就可以避免压力速度定义在同一点产生的压力棋盘格式，也可以避免连续方程通量计算中的差值守恒性和Poisson方程边界条件问题.动量与压力的解耦求解采用分步方法[7].

图1 u方向的交错网格及u分量控制体Fig.1 Staggered grid in u direction and u component control body

由上可知，得到u方向的动量方程：

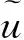
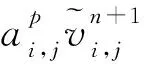
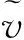
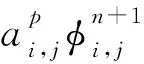
其中φ与压力项p有关，即

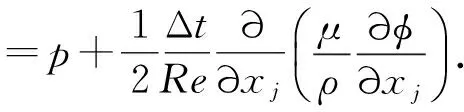
1.2计算域

图2 计算域展示图Fig.2 Computational domain sketch map

在本次模拟计算中，经无量纲化处理将圆柱直径设为1，选取长l=16，宽d=4的长方形计算域，串列双圆柱的间距比为2，上游圆柱圆心位置与进口边界的距离为4，如图2所示.

在以往的计算中，研究者大多将计算区域网格采用分块的结构化网格，圆柱周围计算区域采用O型网格，由于涡的产生、发展和脱落的整个过程均在圆柱表面进行，圆柱表面附近区域的计算网格划分和网格质量对圆柱表面的计算结果会产生较大的影响，因此采用O型网格的优势是能够更好地模拟圆柱体表面上涡的产生和发展过程.但是在圆柱表面区域生成正交性较好的高质量网格却比较困难.

由于模拟中的求解域和圆柱截面的网格均为比较规整的形状(Cartesian正交网格)，且网格点数较高(1026×514)，使得圆柱表面计算精度比较高.整体网格在空间为非均匀分布，在圆柱周围进行了加密，如图3(a)所示的网格整体效果，图3(b)为将网格放大后的效果.可以看到圆柱附近网格的不均匀性.由于计算的雷诺数较低，使得圆柱附近的边界层不需要太密的网格分辨率，因此使得计算结果具有物理可靠性.

图3 计算网格和圆柱边界层附近计算网格的放大图Fig.3 Computational grid and large version of computational grid near the cylinder boundary layer

1.3边界条件

入口边界条件： 入流为均匀流，u=u0=1，pi+1,j-pi,j=0；

出口边界条件： 出口充分发展ui+1,j-ui,j=0,vi+1,j-vi,j=0；

圆柱表面无滑移边界，给定速度和压力，u=0，v=0；

外壁面无滑移边界，给定速度，(u,v)=0.

2 计算结果分析

本论文主要研究Re=800时，来流为层流时串列双圆柱的绕流情况，分析展示了流动分离、漩涡生成和脱落、漩涡之间以及漩涡-壁面的互相干扰等流体力学现象，得到非定常流动失稳后的一系列固有频率与本征正交分解(Proper Orthogonal Decomposition, POD)模态分析等物理量的对应关系.计算考虑来流为均匀流动，总时间推进长度为300，时间步长为Δt=0.0006，推进时间步为500000步.图4展示了充分发展时刻的流场瞬间结构，以作为对串列双圆柱流场的感性认知.

图4 均匀来流的串列双圆柱绕流的两个瞬时刻流场结构Fig.4 Two moments of instantaneous flow structure about double cylinders in tandem as incoming flow is uniform

图5 串列双圆柱求解域布点情况Fig.5 Domain distribution of double cylinders in tandem

本文选取的圆柱间距比为2.由于求解域为上下对称，因此只需在对称轴以上布点(如图5)，从多尺度层面去探究圆柱绕流脱落事件与频率的关系.从左到右依次记为1，2，3，…，12列，共12×12个研究点.

2.1来流为均匀流时的流场频谱分析

2.1.1 上下游圆柱之间流场信息分析

由图4的流动显示图可知，因为上游圆柱边界层扰动影响，会在两圆柱之间产生旋涡.文献[8]显示，当Re=60～200时，双柱串列绕流存在一个临界间距比(l/d=3.6)，小于临界间距时，上游圆柱不存在涡脱落.在本算例中根据流动显示图及后续的证明，得到当Re=800，两圆柱间距比为2时，上游圆柱也不存在涡脱落.在两圆柱的共同作用下，该区域形成有规律的涡结构.对两圆柱中间的3列点进行分析得到速度场信息和速度场的频谱分析.选择其中3个典型位置： 第4列第1个点(0.68,0)、第5列第2个点(0.99,0.14)、第6列第3个点(1.29,0.29)，得到如图6(见第388页)所示的u和v方向的速度频谱分析图.x轴为频率，记为f(=t-1)；y轴为振幅，u方向的振幅记为Au,v方向的振幅记为Av.

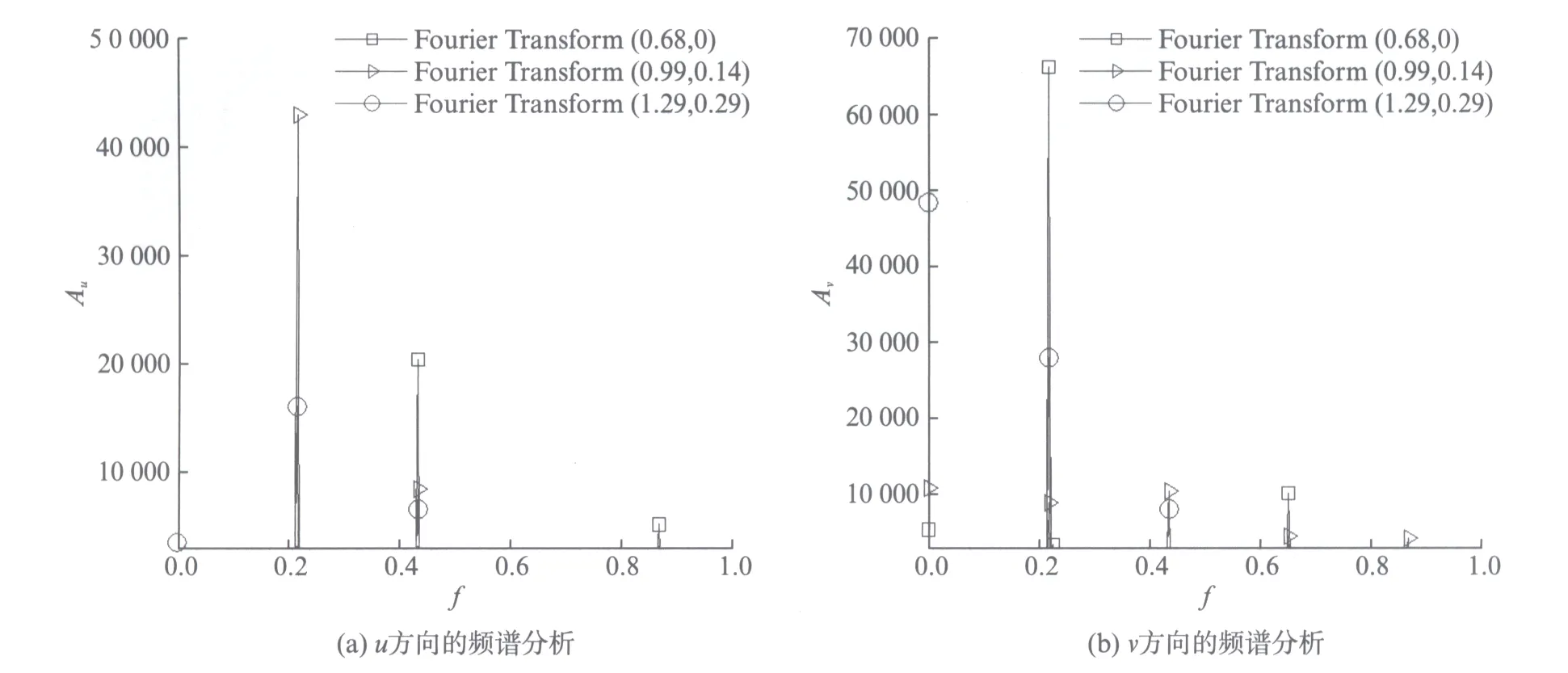
图6 点(0.68,0)，(0.99,0.14)，(1.29,0.29)u和v方向的频谱分析Fig.6 (0.68,0)，(0.99,0.14)，(1.29,0.29) spectrum analysis in u and v direction

以上的频谱分析结果可解释图4中关于两圆柱之间的流动显示观察.从频谱分析图中可明显看出0.22为主导频率，0.44为次主导频率.再结合u，v方向的频谱分析，发现0.22，0.44的频率会在不同的位置起不同的主导作用.上游圆柱的边界层扰动是上下游圆柱之间的涡形成的主要原因，但是涡在此位置的摆动则是上下游圆柱共同作用的结果.

从图4中可以看出，上下游圆柱之间的涡同时在转动和上下摆动，因此生成的涡不是简单一个大尺度涡，而是在震荡的过程中也产生了小尺度的旋涡.大涡频率为0.22，小涡频率为0.44.图4呈现出的结果与频谱分析得出的结果基本相同.另外，从频谱分析图上也可以看到还有一个比较明显的频率0.65，能量不多但也不足以忽视，说明除此两个涡之外仍有一些细碎的小涡形成，频率在0.65附近.

2.1.2 下游圆柱尾流流场信息分析

文献[9]显示，雷诺数达到150和200时，圆柱尾流区出现明显的涡脱落，在圆柱后的尾流区形成了稳定的涡街结构，涡街排列规则.本文的雷诺数为800，图4的流动显示图明显展现了下游圆柱后面有涡的脱落且排列规则.由流体力学知识可知，流体绕圆柱流动时，过流断面收缩，流速沿程增加，压强沿程减小，而由于粘性力的存在，柱体周围形成附面层分离，随雷诺数增加，在柱体后半部分形成不同的绕流尾迹现象，可推测下游涡会同时受到上下游圆柱边界层扰动的影响.

对下游圆柱后面4列点做出u-t，v-t，p-t和对应的频谱分析，如图7所示.结合流动显示图4，近下游圆柱尾流区的涡已经形成但是还未脱落.从图7中可以看到，0.22为最明显的主导频率，0.44和0.65为次要频率.下游圆柱后面的涡发生了脱落，说明0.22为脱落频率.0.44和0.65分别是受上游圆柱和下游圆柱边界层扰动形成的套在大涡里的小涡.理由如下： 1) 上下游圆柱之间的主频出现了0.44，但并没有出现0.65；2) 下游圆柱上方的位置主频出现0.44而没有0.65；3) 下游圆柱主频同时包括有0.44和0.65.两圆柱之间位置的涡只受上游圆柱的影响，而下游圆柱后面的涡同时受到上下游圆柱边界层扰动的影响.

远离下游圆柱的尾涡区，涡已经脱落，涡经过的位置都有3个主要的频率，分别为0.22，0.44，0.65.同样0.22为涡的脱落频率，由前面的分析可知，脱落涡中有两个频率为0.44和0.65的小涡，分别是受上游圆柱和下游圆柱的影响.

由于涡不仅产生了脱落，而且受到上下游圆柱的影响也产生了小涡结构.同时在图7中发现小涡频率除0.44和0.65之外，还有0.91比较突出.说明在这些事件的共同影响下使得流动现象更加复杂，出现了其他频率的小涡结构.选择其中3个典型位置： (2.72,0.73)，(3.92,0.14)，(6.17,0.14)，得到如图7所示的u和v方向的速度频谱分析图.

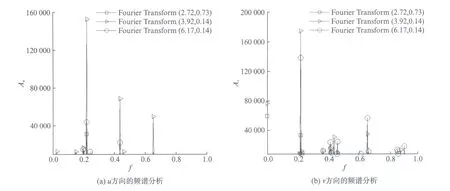
图7 点(2.72,0.73)，(3.92,0.14)，(6.17,0.14)u和v方向的频谱分析Fig.7 (2.72,0.73)，(3.92,0.14)，(6.17,0.14) spectrum analysis in u and v direction

图7展示了下游圆柱尾流区特定位置涡的特点，在研究中也发现，同一列12个点的位置涡的能量呈现一定的变化规律，如图8展示．以x=3.92列为例，比较同一列上的位置，发现u方向上主频率的能量从标记1处向上开始逐渐增加，到3处到达最大之后衰减；v方向上主频率的能量从标记1处达到最大，向上开始逐渐衰减.再以x=6.17列为例，u方向上主频率的能量从标记1处向上开始逐渐增加，到5处到达最大之后衰减；v方向上主频率的能量从标记1处达到最大，向上开始逐渐衰减.说明涡脱落之后的轨迹并不是一条水平线，且其水平方向的能量最大值随涡的移动而变动，竖直方向的能量随位置的升高而降低.可推测水平方向能量的最大值在涡的中心位置.在x=6.17列的折线图中看到最低点之后有回升，结合流动显示图，说明求解域的边界层在此处已经变宽，x=6.17列标记12已经触及求解域的边界层.在这篇论文中不对边界层做深入的研究.

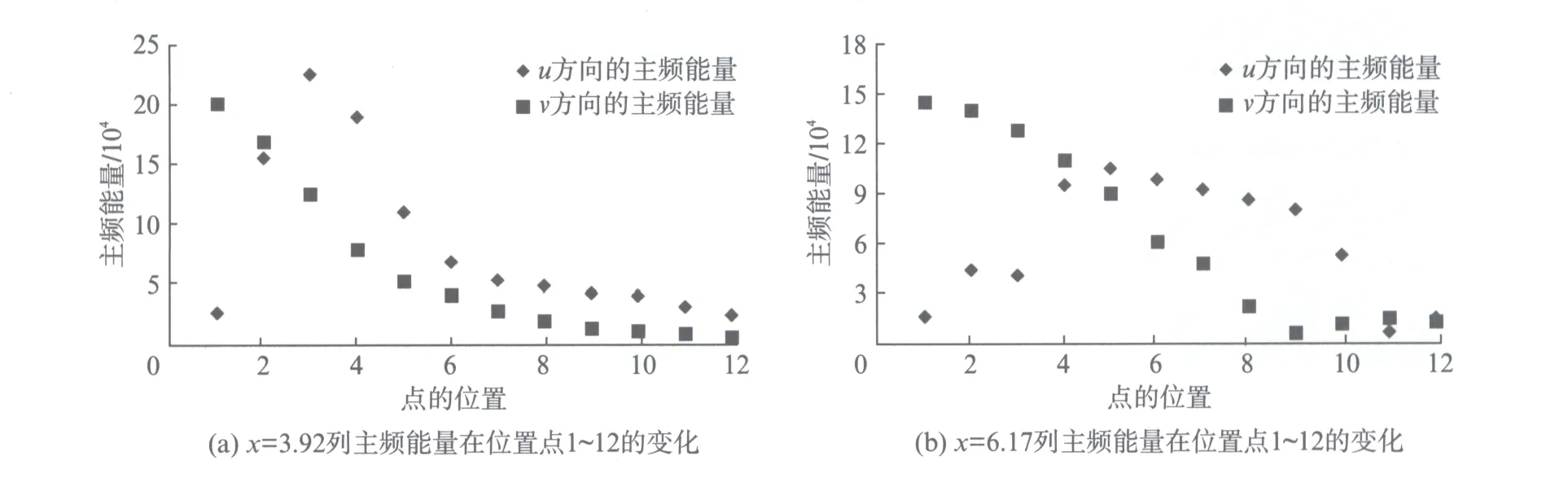
图8 x=3.92和x=6.17列主频能量的变化Fig.8 Line x=3.92 and x=6.17 energy change of dominant frequency

2.1.3 结果对比

在文献[1]中，刘松等在Re=200，间距比为2，串列双圆柱绕流的情况下，数值模拟得到Strouhal数为0.19，同等条件下文献[10]的实验结果中Strouhal数为0.13，而在本文中Re=800，间距比为2，由St=fD/u0(式中St为斯特劳哈尔数，f为频率，D为圆柱直径，u0为初速度)[10]得到Strouhal数为0.22，在同一数量级，这说明本文的模拟计算结果与其他类似研究的可比性及可靠性.

2.2均匀来流的流场模态分析

图9 1～20阶模态能量衰减图Fig.9 1—20 mode energy attenuation map

上文在多尺度层面解释了串列双圆柱在Re=800，来流为均匀流时的流动结构以及影响原因.由于湍流多尺度的复杂性，为了研究湍流的物理机制，研究人员常用模态分解的办法来提取对流场发展有重要影响的相干结构.POD法是按照能量的大小对各模态进行排列，提取流场中较大能量的结构.POD目前已用于研究多种流动问题，例如低雷诺数下圆柱绕流的动态特性.在本篇论文中，将多尺度微观层面流场结构分析和POD法模态分析结合，来解释串列双圆柱绕流的流动现象.

将计算得到的前20阶模态能量作线形图，如图9所示，可以看到前2阶能量大幅衰减.

根据能量占比计算得到，前8阶能量已经占到总能量的94%，所以取前8阶模态为POD分析的对象，如图10所示.

图10 1～8阶模态涡量云图Fig.10 1—8 vortex cloud chart

图10是串列双圆柱绕流前8阶模态的涡量云图，根据图10，1，2，4，6，7阶模态在垂直于流动方向上为正对称结构，3，5，8阶模态在垂直于流动方向上为反对称结构.和图4的流场结构显示图结合可以从整体上对该流场有直观的感受，可以看到流场涡尺度的多样化和涡结构的复杂.下面将通过频谱分析将模态、涡结构以及流场的影响因素联系起来.图11为1～8阶模态的速度频谱图.

图11 1～8阶模态u方向速度频谱图Fig.11 1—8 mode in u direction velocity frequency spectrum

1,2阶模态中只有主频率0.22的涡，且第1阶模态包含88.5%的能量，前2阶模态包含90.8%的能量，说明涡脱落发生在第1阶模态，2阶模态相对于1阶模态多一些扰动.3阶模态中的主频为0.44和0.91，说明上游圆柱边界层扰动的影响主要发生在3阶模态中.4阶模态包含4个主频，说明4阶模态涵盖了下游圆柱尾流涡结构的所有信息，也体现了上下游涡共同作用的结果.除4阶模态之外，7阶模态和8阶模态也都包含了4个主频，但明显7阶模态中频率0.91的影响比较小，说明涡脱落时结构中主要包含3个涡，而在8阶模态中频率0.65的能量相对频率0.44对应的能量更大些，说明在此阶模态中，下游圆柱边界层影响效果更大.5阶模态体现了上下游圆柱中间位置涡的结构，主要受上游圆柱边界层扰动的影响，频率0.22能量占比并非最大.6阶模态中体现了下游圆柱边界层扰动对涡结构的影响，主要频率为0.22,0.65.这8阶模态中由不同原因造成的涡结构的不同，其流场信息结构也可由图10的云图定性地看出.表1为1～8阶模态的能量占比信息及发生涡的主要频率.

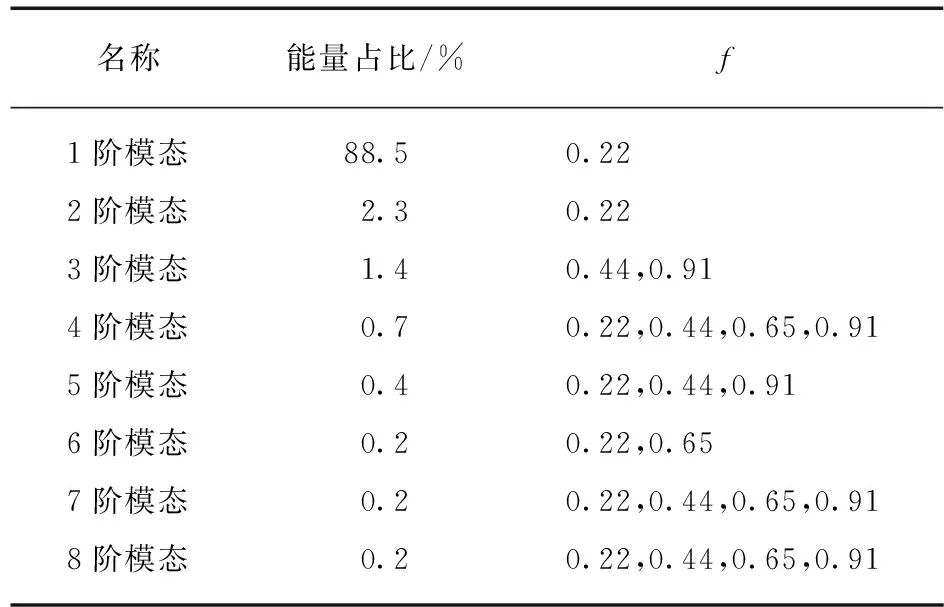
表1 1～8阶模态的能量占比信息及发生涡的主要频率

结合表1以及各阶模态系数频谱分析图11，由于2～8阶模态的能量占比非常小，可知一阶模态的能量即为涡脱落的能量，即主频0.22的能量占88.5%.上下游圆柱扰动影响造成的次主要涡结构总能量占比不到5.5%，其中受下游圆柱层流扰动影响形成的涡能量占比最大，即频率0.65的能量占比排第二，频率为0.44和0.91的能量占比相近.

3 结论与展望

本文从多尺度层面研究了串列双圆柱的绕流问题，分析了Re=800,来流为均匀流时的复杂流场结构，并采用POD方法将能量绝对占优的前8阶模态进行剥离，从而探求涡流场结构及其成因以及与相关模态之间的关系.总体而言，本文做了以下的工作并得出相应结论：

1) 间距比为2时，上下游圆柱之间的涡不会脱落，且通过频谱分析此时除了主频为0.22的大涡之外，内部还套有主频为0.44的小涡，且由上游圆柱边界层扰动产生.

2)Re=800来流为均匀流时流场结构已经呈现多尺度的复杂性.在下游圆柱的后面，出现了涡的脱落且脱落频率为0.22；除此之外，还出现了多尺度的小涡，受上游圆柱边界层扰动产生的频率为0.44的小涡和受下游圆柱边界层扰动产生的频率为0.65的小涡，以及相互之间作用产生的更微尺度的频率为0.91的涡.

3) 将模态与流场结构对应起来，发现由于不同原因产生的涡有些只发生在某一个模态中，有些则在多个模态中发生.前8阶模态的能量占据总能量的94%.

本文只是对Re=800，均匀来流的情况加以分析，对于此雷诺数下来流为湍流的以及高雷诺数比如Re=1600，来流分别为均匀流和充分发展湍流的情况，后续仍需要大量的工作对其进行分析以及对比，才能更深入地从微尺度层面将串列圆柱的绕流问题研究清楚.

[1] 刘松,符松.串列双圆柱绕流问题的数值模拟 [J].计算力学学报，2000，17(3)： 260-266.

[2] ROSHOKO A. On the development of turbulent wakes from vortex streets [R]. Kitty Hawk, North Carolina, USA： National Advisory Committee for Aeronautics, 1954.

[3] ZDRAVKOVICH M. Review of flow interference between two circular cylinders in various arrangements [J].ASMEJournalofFluidsEngineering, 1977,99(4)： 618-633.

[4] PHUOCLOC T, BOUARD R.Numerical solution of the early stage of unsteady viscous flow around a circular cylinder： A comparison with experimental visualization and measurements [J].JournalofFluidMechanics,1985,160： 93-117.

[5] 邓见，黄钰期，任安禄.分块法研究圆柱绕流升阻力 [J].力学与实践，2004，26(1)： 24-26.

[6] 廖俊，景思睿.高雷诺数下双圆柱绕流的数值模拟 [J].水动力学研究与进展，2001，16(1)： 101-110.

[7] KIM J, MOIN P. Application of a fractional-step method to incompressible Navier-Stokes equations [J].JournalofComputationalPhysics, 1985,59(2)： 308-323.

[8] CARMO B S, MENEGHINI J R. Numerical investigation of the flow around two circular cylinders in tandem [J].JournalofFluidsandStructures, 2006,22(6)： 979-988.

[9] 洪文鹏，周云龙，刘巍.圆柱绕流漩涡脱落的数值模拟 [C]∥朱德祥.第七届全国水动力学学术会议暨第十九届全国水动力学研讨会文集(上册).北京： 海洋出版社，2005： 6.

[10] SLAOUTI A, STANSBY P K. Flow around two circular cylinders by the random-vortex method [J].JournalofFluidsandStructures, 1992,6(6)： 641-633.

Abstract： Two-dimensional flow around double cylinders in tandem was calculated, using the finite volume method. Based on the comparisons of the Strouhal number and the lift and drag coefficients with the relevant researches, the flow field and its vortex structure were further investigated. Flow visualizations were conducted and the spectrum and POD analyses were performed to study the vortex shedding and their respective interactions.The formation of the smaller vortex scales were found due to the vortex interactions. The vortex structure and the modes of flow-field exhibited their distinctive structures in terms of their symmetrically and unsymmetrically characteristic distributions in space.Keywords： double cylinders in tandem; direct numerical simulation; multi-scale flow; vortex shedding; shedding frequency

Multi-scaleAnalysisofNumericalSimulationaboutFlowaroundDoubleCylindersinTandem

CUI Xueyang, CAO Bochao, XU Hongyi

(DepartmentofAeronauticsandAstronautics,FudanUniversity,Shanghai200433,China)

F830.9

A

0427-7104(2017)03-0384-09

2016-11-24

国家自然科学基金重大研究计划培育项目(91434112)；上海千人计划启动项目(EZH2126503)；上海教育委员会、中航商业发动机、复旦大学数值仿真联合创新中心项目(AR908.D1RW.002)

崔雪扬(1991—)，女，硕士研究生；徐弘一(1963—)，男，研究员，通信联系人，E-mail： hongyi_xu@fudan.edu.cn.