一种基于低秩表示的高光谱图像恢复方法

蔡荣荣，王 斌

(1. 复旦大学 电磁波信息科学教育部重点实验室，上海 200433；2. 复旦大学 信息科学与工程学院 智慧网络与系统研究中心，上海 200433)

一种基于低秩表示的高光谱图像恢复方法

蔡荣荣1,2，王 斌1,2

(1. 复旦大学 电磁波信息科学教育部重点实验室，上海 200433；2. 复旦大学 信息科学与工程学院 智慧网络与系统研究中心，上海 200433)

高光谱图像(HSI)在获取过程中不可避免地受到各种噪声的干扰，如高斯白噪声、冲击噪声、坏死的线条等．为了确保后续应用能够顺利进行，高光谱图像的恢复是一项重要的预处理过程．文中提出一种新的高光谱图像恢复方法，主要有以下两点贡献： 其一，将低秩表示模型引入到高光谱图像恢复中；其二，利用高光谱图像的相似图像块进行联合低秩表示．模拟和实际高光谱图像数据的实验结果表明，所提出的方法能有效地去除各种噪声干扰，同时较好地恢复图像细节，因此可作为一种实现高光谱图像恢复的有效手段．

高光谱图像；低秩表示；相似图像块；联合；恢复

近年来高光谱图像(Hyperspectral Imagery, HSI)由于其丰富的光谱信息，有着广泛的应用，特别是在精准农业、植被生态、地质矿产、大气环境监测等领域中有较大的应用价值．但是高光谱图像在获取过程中不可避免地受到各种干扰，例如高斯白噪声、稀疏的冲击噪声、坏死的线条等．这不仅使图像的目视效果变差，更对高光谱图像的上述应用造成很大的影响．因此高光谱图像的恢复是一项很重要的预处理过程，其图像恢复的效果将直接影响高光谱图像后续应用的精度．

高光谱图像的恢复研究一直是高光谱领域比较活跃的研究课题．迄今为止，国内外学者已经提出了多种不同的高光谱图像恢复方法．传统的高光谱图像的恢复方法将每一个波段视为独立的二维图像，对各波段逐一应用比较成熟的二维图像的去噪方法，比如基于小波的方法[1]、基于全变分(Total-Variation, TV)的方法[2]、三维块匹配(Block-Matching 3-D, BM3D)算法[3]等．这样的逐波段恢复方法只利用了各个波段自身的空间信息，忽略了不同波段之间的相关性，对于某些受到强烈噪声影响的波段恢复效果较差．

不同于逐波段对高光谱图像进行处理，有学者将高光谱图像看作一个三维图像，提出了多维度的高光谱图像恢复方法．例如，Letexier和Bourennane[4]将高光谱图像看作是一个三维张量，使用Tucker张量分解模型，引入了广义的多维维纳滤波对其进行恢复；而文献[5]使用PARAFAC(Parallel Factor Analysis)张量分解模型对高光谱图像进行恢复．更进一步，有学者将BM3D方法拓展到三维图像上，提出了视频三维块匹配(Video Block-Matching 3-D, VBM3D)算法[6]．VBM3D对于各个波段统计特性相同的噪声恢复效果较好，但是在高光谱图像中，各种类型噪声的存在导致各个波段的噪声强度不一，VBM3D对于这种情况下的恢复效果就显得不够了．

近几年来，国内外学者将低秩矩阵的概念引入到高光谱图像恢复领域中[7-9]，取得较好的效果．文献[7]引入低秩矩阵的概念去除高光谱图像的坏死线噪声，考虑到局部的几何结构并添加了图的正则化．文献[8]基于低秩矩阵恢复(Low-Rank Matrix Recovery, LRMR)较为成功地去除了高光谱图像的混合噪声，其正是得益于无噪的高光谱图像数据低秩的特性．文献[9]在LRMR的框架下添加了TV的正则化，进一步提升了图像恢复效果．但是，LRMR框架是基于鲁棒主成分分析(Robust Principal Component Analysis, RPCA)模型．在RPCA的基础上，Liu等将RPCA发展到低秩表示(Low-Rank Representation, LRR)模型[10]，认为低秩的数据可以源自于多个子空间．相较RPCA而言，LRR模型更为符合高光谱图像的线性混合模型．这两年来LRR模型已经被引入到高光谱图像处理领域，用作估计子空间的数目[11]、异常探测[12]，由于其模型更加符合高光谱图像的特点，所以这些方法都较为成功．另外，文献[8-9]的恢复方法只利用了高光谱图像的每一小块图像的局部信息．如果高光谱图像在某些区域受到强烈噪声影响导致某些块的噪声强度很大以及局部信息受到巨大影响，不引入新的信息将很难得到较好的恢复结果．

针对典型低秩分解方法只利用单一图像块的问题，本文提出一种基于LRR的高光谱图像恢复方法．这里，我们将LRR模型引入到高光谱图像恢复领域；更进一步，利用高光谱图像的非局部相似块的信息，以弥补单个块局部信息不足、样本容量不够的缺陷．在所提出的方法中，首先，通过最小二乘估计得到初步无噪的高光谱图像，由于其能够比较好表示数据子空间，从中选取相应图像块的估计结果作为LRR字典可以更好地凸显LRR模型的优势；再根据各个波段的噪声水平加权融合出单幅图像，对单幅图像进行图像块分类，将分类结果对应到三维高光谱图像中，由于融合图像基本不含噪声，分类结果较为准确；最后对于每一高光谱图像块，在同一类中找出多个与之相似的块，进行联合LRR，因为相似图像块的具有相似的低秩结构，联合LRR可以加大低秩样本容量，利于恢复出图像块的低秩结构．低秩恢复得到的重构矩阵不是单一的图像块，而是多个相似的图像块．一方面使用了更符合高光谱图像数据的LRR模型，另一方面使用非局部相似块的信息．仿真和实际高光谱图像的实验结果都表明，所提出方法的性能表现优于现有的典型高光谱图像恢复方法，验证了所提出方法的有效性．另外，对于实验参数的选择，本文也做了详细的分析和讨论．

1 高光谱图像的低秩模型

1.1无噪高光谱图像的低秩特性

基于光谱混合模型，无噪的高光谱图像通常遵循线性混合模型[13]，表示如下：

X=AS，

(1)

其中：X∈n×b为无噪高光谱图像数据，n为像素个数(如果高光谱图像的空间维数为h和w，那么n=h×w)，b为波段个数；S∈P×b为端元矩阵，表示为S=[s1,s2,…,sP]T，si∈b,P为端元个数；A∈n×P为端元矩阵，它的元素ai,j表示在线性混合模型中第j个端元在第i个像素中所占的比例系数．在大部分情况下，高光谱图像中端元的个数远小于波段数或者像素个数[13]，即P·min(n,b)．又由于X是A和S的乘积，所以X的秩满足：

(2)

显然min(rank(A),rank(S))≤P，所以得到如下结论：

(3)

这意味着矩阵X是低秩的，或者说矩阵X的列所张成的光谱空间的维数小于或等于端元个数P．这就证明了无噪高光谱图像的低秩特性．

1.2低秩表示模型

当高光谱图像受到高斯白噪声的微小扰动时，含噪的高光谱图像数据Y∈n×b可以分解成一个低秩的矩阵X和一个微小扰动的矩阵N如下：

Y=X+N.

(4)

主成分分析(Principle Component Analysis, PCA)通过奇异值分解(Singular Value Decomposition, SVD)来完成数据降维，可以有效地从Y中恢复出X．然而当数据中存在比较大的噪声或者异常时，N就用E代替，E的元素为任意大小，此时PCA的效果就不够准确．针对这种情况，研究学者提出了RPCA[14]，把问题归结为以下凸优化问题：

(5)

其中：λ>0为正则化参数；‖·‖*表示矩阵的核范数，为矩阵的奇异值之和；‖·‖1表示矩阵的l1范数，为矩阵元素绝对值之和．

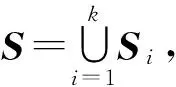
min‖Z‖*+λ‖E‖2，1
s.t.Y=DZ+E，

(6)

其中：λ>0为正则化参数；D为能够生成数据子空间的字典；‖·‖2,1是l2,1范数，表示矩阵每一列的l2范数之和．

解决问题(6)中的优化问题可以得出最优的Z*和E*．Z*可以看成数据Y对于字典D的最低秩表示．由于rank(DZ*)≤rank(Z*)，DZ*可以看成是原始数据Y低秩恢复的结果．噪声由于不能被数据子空间表示，被分离出来，用矩阵E*表示．令D=I，优化问题(6)就退化成(5)．所以LRR可以看成是RPCA模型的更一般的形式，换言之RPCA可以看成是使用了标准基作为字典的LRR模型．

使用增广的拉格朗日乘子法(Augmented Lagrange Multipliers, ALM)求解上述优化问题，先将其转化为以下等价问题：

(7)

通过最小化以下增广拉格朗日函数L可得出最优的Z*和E*：

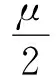
(8)

其中：Y1和Y2为拉格朗日乘子；μ>0为惩罚参数．更详细的求解过程和算法收敛性证明可参考文献[10]．

2 基于低秩表示的恢复方法

2.1空间自适应的相似块的搜寻

图1 含噪高光谱图像中的相似块Fig.1 Similar blocks in the noisy HSI

如前所述，典型的低秩恢复方法都是对单一图像块分别处理的，忽略了高光谱图像中存在非局部的相似块．这些相似图像块对应的地物类型相似且具有很类似的结构特征，导致这些图像块具有相似的空间光谱信息．因此，这些三维图像块在转换为二维图像矩阵后具有近似的低秩特征，也可以理解为由这些二维图像矩阵组成的大图像矩阵的秩与单个图像矩阵的秩是很近似的．如果将这些二维图像放在一起进行联合LRR，无疑可以增加图像矩阵的样本容量，这对于优化问题(6)中从Y中恢复出低秩的部分是有利的．另一方面，由于相似图像块多次参与LRR表示，因此这些图像块有多个低秩恢复的结果，对这些结果加权平均得到最终恢复结果．例如，图1为高光谱图像中一些相似块，在恢复红框里的高光谱图像块时，引入绿框和蓝框里的高光谱图像块来进行联合LRR，这对于恢复红框里无噪图像块的帮助是显而易见的．另一方面，在恢复绿框和蓝框里的图像块时，红框里的图像块被引入到联合LRR，这样红框里的图像块就得到了3次LRR的结果．

本节提出了一种空间自适应的相似块的搜寻方法，分为以下两步： 首先需要将高光谱图像根据各个波段的噪声情况融合成单幅图像．然后将融合后的图像分成相互重叠的图像块，提取每一图像块的局部自适应回归核(Locally Adaptive Regression Kernels, LARKs)[15-16]特征，再将这些图像块聚成K类．

2.2.1 估计各个波段的噪声，将高光谱图像融合成单幅图像

噪声估计在高光谱图像中一直是一个重要问题，也有许多方法可以解决，文中采用基于多重回归理论的方法[17]来进行噪声估计．

用Y=[y1,y2,…，yb]表示含噪高光谱图像，其中Y的每一列yi是高光谱图像第i个波段拉伸成的矢量．用Y∂i=[y1,y2,…，yi-1,yi+1,yi+2,…,yb]表示不含第i个波段的含噪高光谱图像．假设yi可以用剩余的b-1个波段的线性组合表示如下：

yi=Y∂iβi+ξi，

(9)

其中：Y∂i∈n×(b-1)；βi∈(b-1)×1为回归向量；ξi∈n×1为噪声向量．对于每一个i∈{1,2,…，b}，回归向量的最小二乘估计由下式给出：

(10)

然后可得到第i个波段的信号和噪声的估计如下：

(11)

(12)

最后各个波段的噪声方差可由下式得出：

(13)

为了尽可能保留高光谱图像每一个波段的信息，采用加权平均的思想得到融合图像．加权的策略为噪声强度大的波段权值较小，噪声强度小的波段权值较大，具体如下：

(14)

图2 高光谱图像的融合Fig.2 Fusing of HSI

其中权值ω(yi)是通过高斯核函数定义：

(15)

其中：h=max(σi)．上式定义的权值使得那些受噪声影响小的高质量的波段对于融合图像有显著的贡献，使得融合图像的质量得到提升，为之后的图像块分类做好准备．图2为高光谱图像融合成单幅图像的例子，从图中可以看出融合以后的图像噪声强度大大减小，对之后的相似图像块的搜寻大有帮助，也验证了提出的融合策略是正确的．

本小节的目的有两个： 其一，产生高光谱图像的初步无噪估计，为之后LRR模型字典D的选取提供基础；其二，把高光谱图像通过加权融合为单张图像，为了方便后续相似图像快的搜寻．

2.1.2 相似块的搜寻

图3 相似的图像块的聚类过程Fig.3 Clustering of the similar blocks

在2.1.1中已经得到了一幅融合后的高光谱图像，利用滑动窗将融合后的图像分成相互重叠的图像块，每个像素点对应以其为中心的一个正方形图像块．这样，一幅图像分成的图像块个数等于这幅图像的像素点个数．对于每一个图像块，均提取它们的LARK特征，使用K-means[18]方法将这些图像块分成K类，每一类都包含几何特征很相似的图像块．图3所示为K=9时的融合高光谱图像块的聚类结果，着色方案为： 如果以像素i为中心的图像块Yi属于第k类(k=1,2,…,K)，那么像素i就着以第k类所对应的颜色．从图中可以看出即便图像存在噪声，使用LARK特征对图像块进行聚类得到的效果也是较准确的．使用LARK特征的聚类结果比较依赖参数K，一方面K比较小时会导致结构不相似的图像块被聚在同一类中，对后续处理产生影响；另一方面，K比较大的时候会导致每一类的图像块数量太少，使得后续处理的图像块样本量不够．参数K对于实验结果的影响，将在实验中进行进一步分析．

对融合后的图像完成相似图像块的聚类之后，将此结果对应回三维高光谱图像中，就可以得到三维高光谱图像块的聚类结果了．对于每一高光谱图像块，之后相似块的选取均在和它同类的块中进行寻找．

2.2基于联合低秩表示的恢复方法

提出的基于联合LRR的高光谱图像恢复算法可以细分为以下3步： 图像块的组合、联合矩阵LRR的求解和高光谱图像的恢复．

(16)

(17)

最后，通过低秩恢复得到的图像矩阵，重构出无噪高光谱图像．

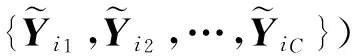
(18)

(19)

其中：τ是一个调节图像块相似性对于权值影响的参数；di,ij表示图像块Yi和Yij的块相似度．

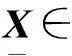
3 实验验证

在本节中，分别使用模拟图像数据和实际图像数据来证明提出方法的图像恢复效果，并对比了VBM3D[6]和LRMR[8]方法．进一步地，为了证明LRR模型的有效性，对每一高光谱图像块，使用LRR模型恢复出其低秩结构，将此方法称为LRR方法；另外，为了证明引入相似图像块的作用，对于每一高光谱图像块，找出和它最相似的一些块，进行联合LRMR，将此方法称为联合LRMR方法，即联合LRMR和联合LRR方法的唯一区别在于进行低秩分解时一个采用LRMR模型，另一个采用LRR模型．我们将LRR和联合LRMR方法也作为对比方法．在实验开始之前，将高光谱图像数据的每一个波段的像素值都归一化为[0,1]．VBM3D方法中噪声的方差由2.1.1中估计得到；LRMR方法的参数采用文献[8]的选择；联合LRMR方法中图像块大小与LRMR一致．

3.1模拟图像实验及评价指标

模拟图像实验选用了2个高光谱图像数据集： 帕维亚大学(Pavia University)数据集和华盛顿特区中心(Washington D.C. Mall)数据集．Pavia University数据集的空间大小为610×340，包含103个波段．实验1中选取了大小为100×100×103的子图像为实验对象．Washington D.C. Mall数据集的空间大小为1208×307，包含191个波段．实验2中选取了大小为100×100×103的子图像为实验对象．

在模拟实验中，对2个数据集均添加以下3种噪声： 每个波段都添加σ=0.1的高斯白噪声，模拟实际中的热噪声；在波段20，40，41，60，61，80，81随机选择5%的像素点加入σ=0.7稀疏高斯白噪声，模拟实际中的像元坏死；在波段21，31，41，51，61，71，81波段随机添加4条坏死的线条，模拟实际中的传感器故障．

本文采用2个评价指标，峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)和结构相似性(Structural Similarity, SSIM)指标[19]定量地对恢复结果进行评价．对无噪图像和恢复图像逐波段计算PSNR和SSIM值，然后取平均得到平均PSNR(Mean PSNR,mPSNR)和平均SSIM(Mean SSIM,mSSIM)值．各个指标的定义如下：

(20)

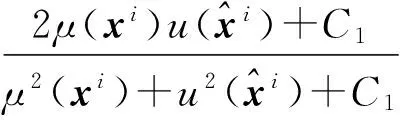
(21)

(22)

(23)

3.1.1 实验1

实验1采用Pavia University数据集，提出方法的实验参数选取如下： LRR的参数λ=0.35、滑动窗即图像块的大小Wsize=11、图像块聚类的类数K=10、相似图像块的数量p=5、式(19)的参数τ=10．Pavia University数据集的第61波段无噪图像如图4(a)所示，图4(b)是添加了3种噪声的含噪图像，图4(c)～(g)分别是使用VBM3D、LRMR、LRR、联合LRMR和联合LRR方法恢复后的图像．从图中可以看出，VBM3D方法对于强烈的稀疏噪声和坏死的线条去除效果较差，因为它所使用的模型只能去除高斯白噪声．更糟糕的是，由于VBM3D使用联合维纳滤波对图像进行处理，导致它对图像有过平滑的趋势，例如图4(c)右上角的模糊说明了这一点．LRMR、LRR、联合LRMR和联合LRR方法由于使用低秩模型，不仅可以去除高斯白噪声，也可以去除强烈的稀疏噪声和坏死的线条，恢复出比较好的图像．不过，从图中可以看出，LRMR方法不能完全去除所有噪声，LRR方法相较LRMR方法的恢复效果要好一些，说明LRR模型比LRMR模型更适合于高光谱图像的恢复．但是图4(e)红色圈出的区域受到噪声影响，LRR方法的恢复效果并没有很好，存在一些涂抹痕迹．提出的方法将相似图像块组合到一起进行联合LRR，引入了相似图像块的信息增加了低秩矩阵的样本容量，更好的帮助恢复出不含噪声的高光谱图像．从图4(g)看出所提出方法不仅可以去除所有类型的噪声，同时还比较好地恢复出了图像的空间结构，如红色圈出的区域的恢复效果就好于LRR方法．另外，联合LRMR相比LRMR方法恢复效果的提升也能说明引入相似图像块的作用．

图4 Pavia University无噪图、含噪图和不同方法恢复结果的第61波段Fig.4 Band 61 of Pavia University clean data, noisy data and restoration results by different methods

为了进一步定量地评价提出方法的恢复效果，逐波段计算了不同方法恢复后的高光谱图像的PSNR和SSIM值，结果如图5所示．在波段20，21，31，40，41，51，60，61，71，80，81上，所有方法的PSNR和SSIM值均有不同程度的凹陷，原因为在这些波段上存在多种类型噪声，导致图像质量急剧下降．从图中可以看出，提出方法的各波段的PSNR和SSIM值均好于其他方法，特别是在上述波段上，提出方法取得了更大的改善．VBM3D方法只能去除高斯白噪声，所以在具有别的噪声的波段上PSNR和SSIM值均比较低．其余4种方法虽然在不只有高斯白噪声的波段上PSNR和SSIM值有所降低，但是总体效果还是比较好的．尤其是提出方法，不仅在含有3种噪声类型的波段上保持较高的PSNR和SSIM值，在只含高斯白噪声的波段的PSNR和SSIM值也比其余方法要高，这说明引入相似图像块，对于各种噪声的去除效果均具有提升．

图5 不同方法恢复的图像的PSNR和SSIMFig.5 PSNR and SSIM of restoration results by different methods

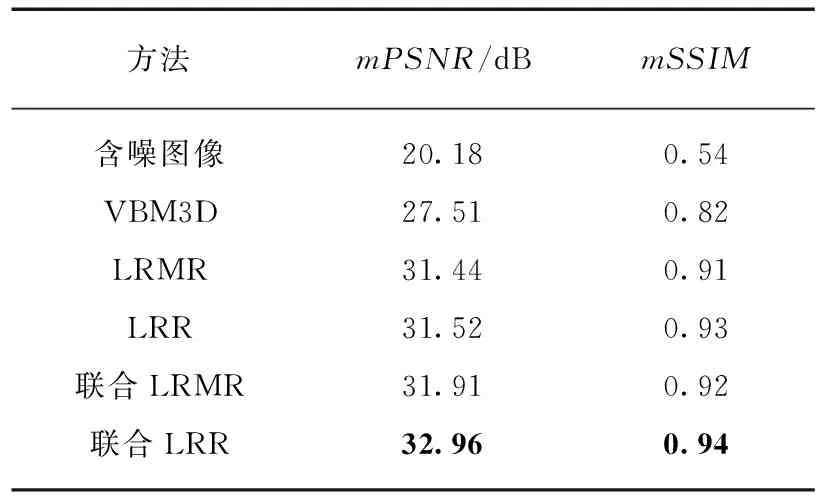
表1含噪图像和不同方法恢复结果的mPSNR和mSSIM

注： 加黑表示性能最优．

表1为各种方法恢复图像的mPSNR和mSSIM值．LRR方法的mPSNR和mSSIM均比LRMR高，说明了LRR模型的优势．联合LRMR方法的mPSNR和mSSIM也比LRMR高，说明引入相似图像块对于低秩矩阵恢复也是有效果的．

3.1.2 实验1的参数分析

实验过程涉及到了5个参数的选取： 式(6)中的正则化参数λ，滑动窗的大小Wsize，图像块聚类的类数K，联合LRR的相似图像块的数量p和式(19)中的参数τ．为了分析讨论这5个参数对于实验结果的影响，对其进行了更详细的实验，采用mPSNR和mSSIM2个评价指标来衡量实验结果．

1) 参数λ

式(6)所述的LRR模型表现的好坏很大程度上取决于参数λ，尤其在实际环境中，由于缺乏数据的先验知识，如何选取合适的λ是一个值得探讨的问题．文献[20]指出在没有先验知识的情况下，λ按照以下式子选择，LRR模型可以得到比较的结果，其中n为高光谱图像的波段数．

(24)

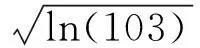
图6 参数λ对于恢复结果的影响Fig.6 Impact of parameter λ to restoration results

2) 滑动窗的大小Wsize

图7给出了恢复结果和Wsize的关系，适中大小的Wsize对于恢复的结果比较好．当Wsize比较小的时候，图像块的像素个数太少，样本量不够，导致恢复效果较差．当Wsize比较大的时候，图像块过大时，它的纹理特征比较复杂，导致应用LARK特征对图像块聚类时准确度下降，进而恢复效果变差．

图7 滑动窗窗边的大小Wsize对于恢复结果的影响Fig.7 Impact of edge size Wsize of sliding window to restoration results

3) 图像块聚类的类数K

K对于恢复结果的影响见表2．从表中可以看出恢复结果对于K的选取并不敏感，原因是只要选取适当的K，使每一类的图像块个数大于等于p．那么对于每一个图像块都能在它所属的类中找出和它最相似的p-1个块，联合进行LRR，得到好的恢复效果．

4) 相似图像块的数量p

表3描述了p对于恢复效果的影响．当p=1时，联合LRR就退化成LRR了．从表3中，可以看出当p从1跳跃到2时，恢复效果有了明显提升，说明引入相似图像块的信息对于图像恢复是有效果的．当p大于5时，mPSNR和mSSIM有些许下降，说明联合LRR的相似块不是越多越好．图像块取多了，比较不相似的块就有可能被引入到联合LRR中，这会影响恢复效果．

表2 图像块聚类的类数K对于恢复结果的影响

表3 相似图像块的数量p对于恢复结果的影响

注： 加黑表示性能最优.

5) 参数τ

参数τ对于恢复结果的影响较小，从表4中可以看出τ的选取对mPSNR的影响不到0.1，对mSSIM的影响不到0.001．因为图像块的权值是经过归一化的，说明τ对于各图像块的融合结果几乎没有影响．

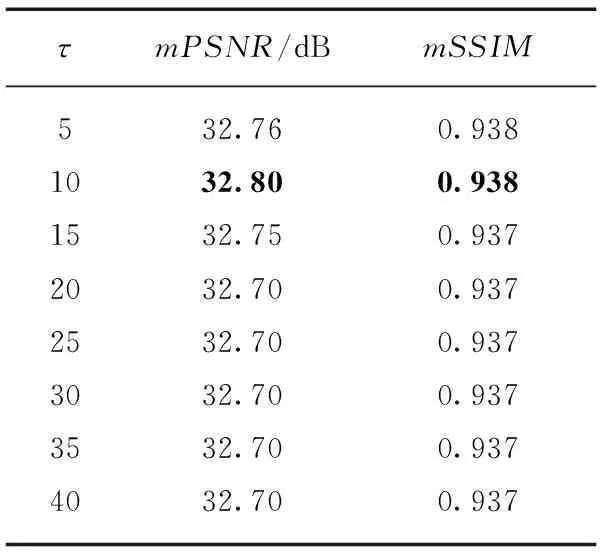
表4 参数τ对于恢复结果的影响

注： 加黑表示性能最优.

总之，从上述的分析可以得出以下几点结论： 参数λ可以在求出α后，通过式(24)得到；滑动窗的大小Wsize适中选取(图7)；相似图像块的数量p在一定范围内选取(表3)；图像块聚类的类数K和参数τ，提出的方法对它们不敏感(表2和表4)．

3.1.3 实验2

实验2采用Washington D.C. Mall数据集，提出方法的实验参数选取如下： LRR的参数λ按照式(24)得出、滑动窗即图像块的大小Wsize=11、图像块聚类的类数K=10、相似图像块的数量p=5、式(19)的参数τ=10．

Washington D.C. Mall数据集的第81波段无噪图像如图8(a)所示，图8(b)是添加了3种噪声的含噪图像，图8(c)～(g)分别是使用不同方法恢复后的图像．和实验1类似，VBM3D方法去除不了强烈的稀疏噪声和坏死的线条，对图像有过平滑的趋势，存在涂抹痕迹．从图中可以看出，LRR、联合LRMR和联合LRR方法对图像的恢复效果均比LRMR好．图8用红色框出的区域受到严重噪声影响，几乎失去了空间结构．VBM3D和LRMR方法均没有重构出这个结构，LRR方法稍许恢复出了结构但是比较模糊，而引入了相似块的联合LRMR和联合LRR方法均恢复出了这个结构，进一步说明了LRR模型的优势和引入相似图像块的作用．

图8 Washington D.C. Mall无噪图、含噪图和不同方法恢复结果的第81波段Fig.8 Band 81 of Washington D.C. Mall clean data, noisy data and restoration results by different methods

图9为逐波段计算不同方法恢复后的图像的PSNR和SSIM值的结果．在部分含多种噪声的波段上，各种方法的PSNR和SSIM值均有不同程度的凹陷，原因和实验一相同．从图中同样可以看出，提出方法的各波段的PSNR和SSIM值均好于其他方法．在不只有高斯白噪声的波段上，所有方法的PSNR和SSIM值均有所降低，VBM3D方法下降最严重．在只含有高斯白噪声的波段上，VBM3D方法的PSNR和SSIM值和其余方法比较接近．LRMR和联合LRMR方法在20～60波段表现不如LRR和联合LRR方法稳定，说明LRR模型比LRMR模型适合于高光谱数据．

图9 不同方法恢复结果的PSNR和SSIMFig.9 PSNR and SSIM of restoration results by different methods

表5为各种恢复方法的mPSNR和mSSIM值．提出方法的mPSNR较VBM3D和LRMR方法分别提高4.16和2.90dB，mSSIM较VBM3D和LRMR方法分别提高0.07和0.03．说明本文提出的方法对于各种噪声去除的效果都很稳定．

3.2实际图像实验

实际图像实验选用了1992年6月拍摄的印第安纳(Indiana)州西北部农业区220个波段的AVIRIS高光谱航空影像，光谱分辨率和空间分辨率分别为10nm和20m，包含了145×145个像素，去除水吸收波段104～108，150～163，220后剩余200个波段，其中好几个波段严重受到噪声干扰．该数据集通常被用于高光谱图像的分类实验中．这里，选取了9类地物，各类地物名称和样本数如表6所示．

噪声的存在会对高光谱图像分类的精度造成影响，所以可以用分类精度来评价对实际图像的图像恢复效果．本文使用支撑向量机(Support Vector Machine, SVM)作为分类器，分类总体精度(Overall Accuracy, OA)作为评价指标(见表7)．每一类地物随机选取10%的样本作为训练样本，其余作为测试样本．Indiana数据集的地物真实与使用原始数据和不同方法处理后的图像的分类结果见图10．

表5 含噪图像和不同方法恢复结果的mPSNR和mSSIM

注： 加黑表示性能最优.

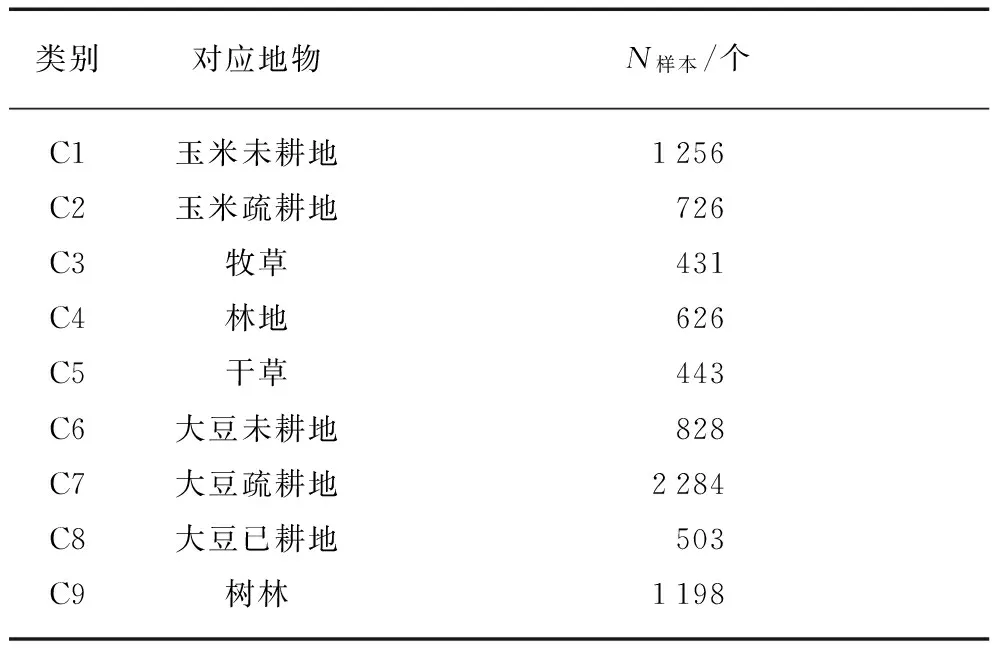
表6 Indiana数据中地物各类别样本数量

注： 加黑表示性能最优.

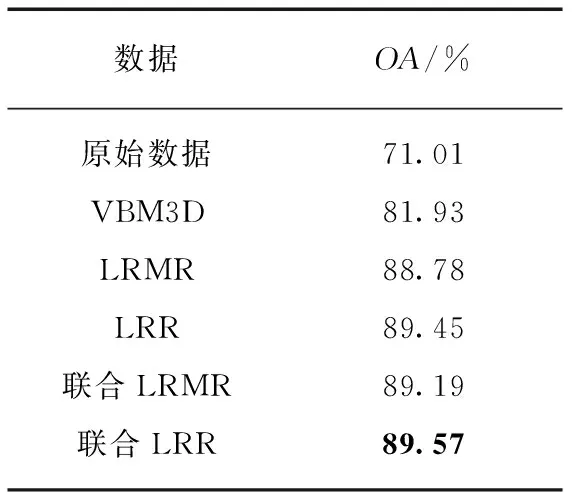
表7使用原始数据和不同方法恢复结果的分类总体精度

注： 加黑表示性能最优.

提出方法的实验参数选取如下： LRR的参数λ按照式(24)得出、滑动窗即图像块的大小Wsize=11、图像块聚类的类数K=10、相似图像块的数量p=5、式(19)的参数K=10．从OA值和分类结果图可以知道，原始数据由于其受到噪声影响严重，导致分类精度较差．在经过不同方法处理后，分类精度均有所上升．由于实际高光谱图像数据受到各种噪声的影响，只能去除白噪声的VBM3D方法对于提升分类精度的能力有限．而之后的4种方法能够去除的噪声类型比较多，所以能够较大地提升高光谱图像的分类精度．提出方法的分类精度较LRMR、VBM3D方法分别高了0.97%和7.64%，LRR和联合LRMR方法的分类精度均比LRMR方法要高，说明LRR模型的确也可以较好地分离噪声和信号，也说明了引入相似图像块在一定程度上是有助于实际图像恢复的．而提出的方法综合了LRR模型的优势和引入相似图像块的作用，对于实际高光谱图像的恢复是有效的．

图10 Indiana数据集的地物真实与使用原始数据和不同方法的恢复结果的分类结果Fig.10 Ground truth of Indiana dataset and results of classification using raw data and restoration results by different methods

4 结 论

本文提出了一种新的高光谱图像的恢复方法．该方法先利用最小二乘估计出各个波段的噪声水平，融合出单幅图像．再对单幅图像提取每一图像块的LARK特征，将图像块聚类．最后对于每一高光谱图像块，在类内寻找相似图像块，组合在一起进行联合LRR．其中由于最小二乘估计的结果已经能比较好地表示数据子空间，所以从中选择相应块的最小二乘估计作为LRR的字典．更进一步，该方法不仅引入了更符合高光谱图像特性的LRR模型，还突破了典型低秩恢复方法只利用单一图像块信息的缺点，利用相似图像块更精确地恢复出高光谱图像的低秩结构．实验结果表明，所提出方法能够在保留图像细节的前提下去除多种类型的噪声，在目视效果和客观评价指标上均优于目前的高光谱图像恢复方法．这对于处理受到各种噪声干扰的高光谱图像来说具有重要的实际意义．

[1] KOPSINIS Y, MCLAUGHLIN S. Development of EMD-based denoising methods inspired by wavelet thresholding [J].IEEETransSignalProcess, 2009,57(4)： 1351-1362.

[2] WEN Y W, NG M K, HUANG Y M. Efficient total variation minimization methods for color image restoration [J].IEEETransImageProcess, 2008,17(11)： 2081-2088.

[3] DABOV K, FOI A, KATKOVNIK V,etal. Image denoising by sparse 3-D transform-domain collaborative filtering [J].IEEETransImageProcess, 2007,16(8)： 2080-2095.

[4] LETEXIER D, BOURENNANE S. Noise removal from hyperspectral images by multidimensional filtering [J].IEEETransGeosciRemoteSens, 2008,46(7)： 2061-2069.

[5] LIU X, BOURENNANE S, FOSSATI C. Nonwhite noise reduction in hyperspectral images [J].IEEEGeosciRemoteSensLett, 2012,9(3)： 368-372.

[6] DABOV K, FOI A, EGIAZARIAN K. Video denoising by sparse 3D transform-domain collaborative filtering [C]∥IEEE Conf Signal Process, European, 2007： 145-149.

[7] LU X, WANG Y, YUAN Y. Graph-regularized low-rank representation for destriping of hyperspectral images [J].IEEETransGeosciRemoteSens, 2013,51(7)： 4009-4018.

[8] ZHANG H, HE W, ZHANG L,etal. Hyperspectral image restoration using low-rank matrix recovery [J].IEEETransGeosciRemoteSens, 2014,52(8)： 4729-4743.

[9] HE W, ZHANG H, ZHANG L,etal. Total-variation-regularized low-rank matrix factorization for hyperspectral image restoration [J].IEEETransGeosciRemoteSens, 2016,54(1)： 178-188.

[10] LIU G, LIN Z, YAN S,etal. Robust recovery of subspace structures by low-rank representation [J].IEEETransPatternAnalMachIntell, 2013,35(1)： 171-184.

[11] SUMARSONO A, DU Q. Low-rank subspace representation for estimating the number of signal subspaces in hyperspectral imagery [J].IEEETransGeosciRemoteSens, 2015,53(11)： 6286-6292.

[12] XU Y, WU Z, LI J,etal. Anomaly detection in hyperspectral images based on low-rank and sparse representation [J].IEEETransGeosciRemoteSens, 2016,54(4)： 1990-2000.

[13] IORDACHE M D, BIOUCAS-DIAS J M, PLAZA A. Sparse unmixing of hyperspectral data [J].IEEETransGeosciRemoteSens, 2011,49(6)： 2014-2039.

[15] TAKEDA H, FARSIU S, MILANFAR P. Kernel regression for image processing and reconstruction. [J].IEEETransImageProcess, 2007,16(2)： 349-366.

[16] CHATTERJEE P, MILANFAR P. Clustering-based denoising with locally learned dictionaries [J].IEEETransImageProcess, 2009,18(7)： 1438-1451.

[17] GAO L, DU Q, ZHANG B,etal. A comparative study on linear regression-based noise estimation for hyperspectral imagery [J].IEEEJSelTopicsApplEarthObservRemoteSens, 2013,6(2)： 488-498.

[18] LLOYD S P. Least squares quantization in PCM [J].IEEETransonInfTheory, 1982,28(2)： 129-137.

[19] WANG Z, BOVIK A C, SHEIKH H R,etal. Image quality assessment： From error visibility to structural similarity [J].IEEETransImageProcess, 2004,13(4)： 600-612.

[20] LIU G, XU H, TANG J,etal. A deterministic analysis for LRR [J].IEEETransPatternAnalMachIntell, 2016,38(3)： 417-430.

Abstract： Hyperspectral imagery(HSI) is unavoidably corrupted by various noises, such as Gaussian white noise, impulse noise, dead lines and so on, in the acquisition process. In order to ensure the performance of subsequent applications, HSI restoration is an essential preprocessing process. A new method for HSI restoration is proposed in this paper with two main contributions： 1) introducing low-rank representation model into the HSI restoration; 2) utilizing similar image blocks for joint low-rank representation. Experimental results on synthetic and real hyperspectral datasets demonstrate that the proposed method can effectively remove various noises and reconstruct the details of image, thus, it should also be used as an effective technique for HSI restoration.

Keywords： hyperspectral imagery; low-rank representation; similar image blocks; joint; restoration

rank(X)≤min(rank(A),rank(S))，

rank(X)≤min(rank(A),rank(S))≤P·min(n,b)，

min‖X‖*+λ‖E‖1
s.t.Y=X+E，

HyperspectralImageryRestorationBasedonLow-RankRepresentation

CAI Rongrong1, 2, WANG Bin1, 2

(1.KeyLaboratoryforInformationScienceofElectromagneticWaves(MoE),FudanUniversity,Shanghai200433,China; 2.ResearchCenterofSmartNetworksandSystems,SchoolofInformationScienceandTechnology,FudanUniversity,Shanghai200433,China)

A

0427-7104(2017)03-0346-13

2016-06-07

国家自然科学基金(61572133)；北京师范大学地表过程与资源生态国家重点实验室开放基金(2017-KF-19)

蔡荣荣(1991—)，男，硕士研究生；王 斌，男，教授，通信联系人，E-mail： wangbin@fudan.edu.cn.