基于吸引子布局算法求解码头泊位岸桥分配问题

司玉军,翁凌韬,郑宗浩,段国林

(1. 河北工业大学 机械工程学院，天津 300130；2. 曹妃甸港集团股份有限公司通用码头分公司,唐山 063000)

基于吸引子布局算法求解码头泊位岸桥分配问题

司玉军1,2,翁凌韬1,郑宗浩1,段国林1

(1. 河北工业大学 机械工程学院，天津 300130；2. 曹妃甸港集团股份有限公司通用码头分公司,唐山 063000)

泊位和岸桥资源是港口码头的重要稀缺资源，如何合理的安排调度船舶靠泊和岸桥工作对港口码头的作业效率有极其重要的影响.同时研究了泊位分配与岸桥调度分配问题，通过将靠泊时间、岸桥使用以及泊位占用进行抽象化，成为一种矩形评价块，并将整体靠泊作业过程转化为一种新的三维矩形布局问题进行研究.计算表明，将传统建模方法转化为空间布局模型可全面考虑靠泊过程中各类型资源的占用，并可有效提高各类资源在靠泊作业中的总体宏观效率，与传统建模和算法相比有明显的优越性和更全面的统筹性.

码头; 调度分配; 吸引子布局算法; 三维布局; 泊位

随着全球经济一体化的快速发展，商业活动对海上集装箱运输服务的需求愈加增强.而港口码头的作业效率的提高，将直接关系到对于海运货物的处理能力以及在港口货运服务市场的竞争能力[1].因此，如何高效地利用港口现有资源快速地完成货运处理任务，对于港方具有极其重要的意义[2].

港口需要众多港口资源配合来进行对货运船舶的作业处理.其中，对于港口而言最为稀缺和重要的资源主要体现在空间资源、设备资源和时间资源[3]，它们将对港口码头产生主要的空间使用成本、设备使用成本以及时间资源消耗成本[4].上述的空间资源、设备资源以及时间资源主要体现为港口的泊位资源、岸桥设备资源以及船舶的在港时间.因此，如何通过合理的调度安排尽可能多地利用这些资源，来完成对货运船舶的处理作业将是至关重要的[5].

由此产生了两个重要的研究问题，即泊位分配问题(Berth Allocation Problem, BAP)和岸桥分配问题(Quay Crane Assignment Problem, QCAP).前者主要决定入港船只的靠泊泊位位置和开始作业时间，后者则决定船只相应地获得的服务岸桥的数量[6].但BAP和QCAP两问题之间具有很强的关联耦合性： 一方面BAP中决定的开始作业时间很大程度上依赖于QCAP中是否在该时刻具有足够数量的空闲岸桥；另一方面，QCAP中决定的对船舶进行服务的岸桥编号和数量，将直接影响BAP中的泊位的位置[7].而当船舶的靠泊位置以及对其进行服务作业的岸桥编号和数量确定后，可以得到相应船舶的实际在港作业时间.所得到的各艘船舶的作业时间，将用于评估该种泊位岸桥调度分配方案的优异程度.由于BAP和QCAP所具有的明显关联性，目前越来越多的学者将它们视为一个单一问题——泊位岸桥调度分配问题(Berth and Quay Crane Assignment Problem, B&QCAP)，并提出了相关的集成调度方法.

早期的研究将泊位视为离散型的多个不同的无关联个体进行研究，而在近年的研究中，越来越多的学者将港口的整个泊位视为一个整体资源，并对不同的船只进行不同的动态划分.根据文献[8]的介绍，实际上可将泊位视为离散型、连续型以及混合型3种泊位形式.在3种划分情况中，离散型泊位对于问题的讨论和模型的简化具有较大的优势，但缺陷在于在实际应用中会有较大的泊位资源浪费；连续型泊位在实际生产应用中具有更强的机动性和灵活性，可以最大限度提高泊位资源的利用率，但相应地也会增加解决问题模型建立的难度和计算的复杂度；混合型泊位则中和了离散型泊位和连续型泊位的优缺点.

根据文献[9]对于船舶的到港情况可分为静态问题以及动态问题两种.但在实际港口的运营中，多以静态问题居多，港方通常会提前得到将到港靠泊作业的船只信息，并进行相关的调度分配.综合考虑上述泊位划分情况、船舶到港计划以及港口实际情况，本文将讨论分析已有船舶静态到港作业任务信息情况下的连续型泊位的泊位岸桥分配调度问题.

1 问题的描述

由上节的介绍中我们可知BAP和QCAP是两个具有耦合相关的问题，在本文讨论中我们将它们结合为一个B和QCAP进行讨论.B和QCAP是一个涉及到多单位、多部门协同调度工作的复杂问题，在港口的实际运营中将会涉及到港口码头的各项设备资源的利用和消耗，其中对港口运营经济成本以及服务质量评价最为重要的是3方面的稀缺资源——泊位、岸桥以及时间.为使得港口的运营效率更高、经济效益更大，在研究中通常将最优目标设定为在港时间最优.但仅将时间最优作为优化目标，而泊位资源和岸桥资源仅仅将其作为优化的约束条件，无法实际反映出另两种稀缺资源的实际重要性.而在实际的作业中，船舶在港口靠泊时的密度，作业的岸桥数量，都将直接影响港口的运营成本和集输效率.

而船舶的整个靠泊作业过程所占用的资源，即岸桥资源、泊位资源和时间资源恰好构成一个矩形块.对于整个港区作业过程的调度分配而言，即相当于在一个有限的三维布局空间中，合理地布局每一块船舶作业资源块，以使得港区的整体资源利用率最高、效率最大.针对该布局问题，结合文献[10]提出了船舶资源占用块布局吸引子的概念.通过吸引子的值来判断布局块各个位置的优劣，以提高整体空间资源的利用率.为便于计算，将泊位的长度以10m为一个单位，船舶的长度也以10m为一个单位，并构建三维布局空间.

为便于模型的建立和后期的分析，本文作如下假设： 1) 该段时间内所有到港船舶固定且到达锚地时间已知；2) 船舶到港后才可以进行服务；3) 每个泊位的水深均满足待泊船吃水深度要求；4) 不考虑偏好位置.

2 模型构建

本文使用的变量符号及其意义如下所示.

V: 将被码头服务的船舶集合，V=[1,I]；

t: 时间的集合，t∈[1,T]，t∈+；

c: 岸桥的集合，c∈[1，C]，岸桥最多数量为C；

li： 船舶i的长度；

L： 码头的长度；

ai: 船舶i的到港时间；

dtai: 船舶i的延时开始作业时间长度；

φ(x): 船舶的靠泊时间与到港时间的差值所导致的惩罚系数；

pi: 船舶i的期望最早离开时间；

dtli: 船舶i的延时离港时间长度；

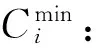
cfi: 第一台给船舶i服务的岸桥编号；

cli: 最后一台给船舶i服务的岸桥编号；

ci: 船舶i所分配的岸桥数；

uti: 船舶i在t时刻正在进行装卸作业则为1，否则为0；

bi: 船舶i的靠泊时间,bi∈[1，T]；

fi: 船舶i的结束作业时间,fi∈[1，T]；

ti： 船舶i的作业时长.

问题的约束条件及目标函数如下：

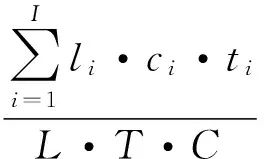
(1)

φ(x)=1-e-θ x，

(2)

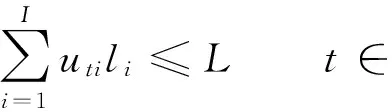
(3)

(4)

ai≤bii∈V,

(5)

pi≤fii∈V,

(6)

(7)

cli-cfi+1=cii∈V,

(8)

dtai=bi-aii∈V,

(9)

dtli=fi-pti∈V,

(10)

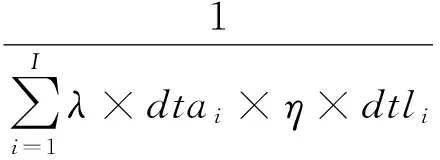
(11)

式(1)为本文所求的目标函数，fmax为整个作业的结束时间，即令港口资源利用效能最大；式(2)为延迟惩罚函数，θ为一实数，具体大小由实际情况而定；式(3)保证在整个港口作业时间内任意t时刻同时在泊的总船长不超过码头最大长度；式(4)保证在整个港口作业时间内任意t时刻同时进行作业的岸桥总数不超过码头岸桥总数；式(5)表示船舶i的到港时间不超过船舶的靠泊时间；式(6)表示船舶i的理论最早结束作业时间不超过实际船舶离港时间；式(7)表示分配给船舶i的岸桥数量在i船所允许的最大岸桥数量和最小岸桥数量之间；式(8)保证为第i艘船舶服务的岸桥连续性；式(9)表示船舶的靠泊时间与到港时间差；式(10)表示船舶离港时间与理论最早完成时间之差；式(11)表示延迟惩罚函数变量.

3 算法设计

在实际作业过程中，每艘船舶的待布局资源占用块是各不相同的，即其资源占用的空间矩形形状各异.为了确保对所有资源占用块的布局合理，使得资源占用效率最高并减少靠泊作业过程中的资源浪费，应当尽可能地使各艘船舶的资源占用块紧凑.

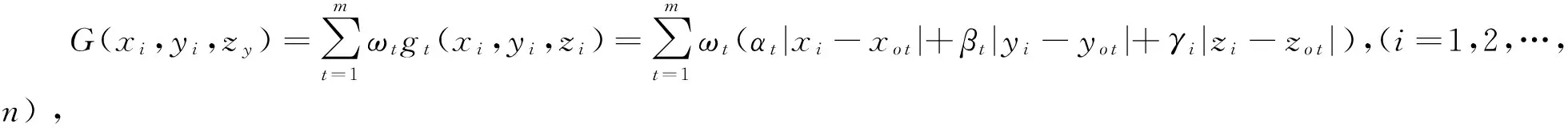
针对这一模型需求，本文结合布局问题的相关理论，采用一种基于布局方法的启发式算法.该算法的核心思想即寻找各艘船舶的合理靠泊位置和岸桥数量，使得总体船舶资源占用块在整体可布局空间中的使用率最大，以使得码头资源的综合利用率最高.其算法步骤如下：

1) 首先，根据船舶的到港顺序ai，产生各自船舶资源占用块的布局顺序；

3) 若待布局资源占用块为第一艘船属性，则根据布局问题中的“占角原则”，将第一艘船舶的资源占用块布局至待布局空间角起始位置，即码头起点、第一台岸桥位置处；若待布局资源占用块为其他船舶属性，则依据步骤1)中产生的布局顺序，计算当前待布局矩形块在各位置的吸引子大小，并选择布局位置，同时将该船舶资源占用块布局至满足约束条件下的位置；

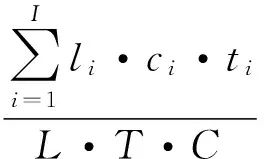
5) 选择操作采用比例选择算子，按个体的适应度采用旋转法决定个体被选择的概率；

6) 交叉操作采用多基因位交叉，在染色体上随机选取多点基因，并将两条染色体上的基因进行交换，以提高染色体的多样性；

7) 变异操作采用单点变异，在染色体上随机选取单点基因，进行基因突变；

8) 循环迭代，直至达到预设最大迭代次数；

9) 输出最终调度方案.

4 算例分析

表1 各船型靠泊时间-岸桥数量表

表2 到港船舶属性表

为检验本算法，取河北唐山市某港口码头数据，码头长度为900m，岸桥数量为10台，港口码头船舶的到港时间服从指数分布，到港船型主要有3类，船舶吨位分别为10000，15000，18000t，3类船船长分别为150，250，310m.经测算，不同台数岸桥对不同型号船舶的工作效率如表1所示.

取某天到港船舶数据进行计算，其相关属性如表2所示.

使用本文介绍的算法，将表2中各船舶船长等信息转化为相应模型系数并进行编码和求解，求得最佳布局调度方案如表3所示.

最终求得的调度方案虽然在总体作业时长上相比传统优化最省作业时间方法略有提高，但整体作业效率和码头资源的利用率得到有效提高，减少了操作工人的工作强度，降低了操作过程中的差错率，同时也降低了设备的使用强度，在实际上提高了码头的整体服务水平，使得码头资源得到更高效地利用.

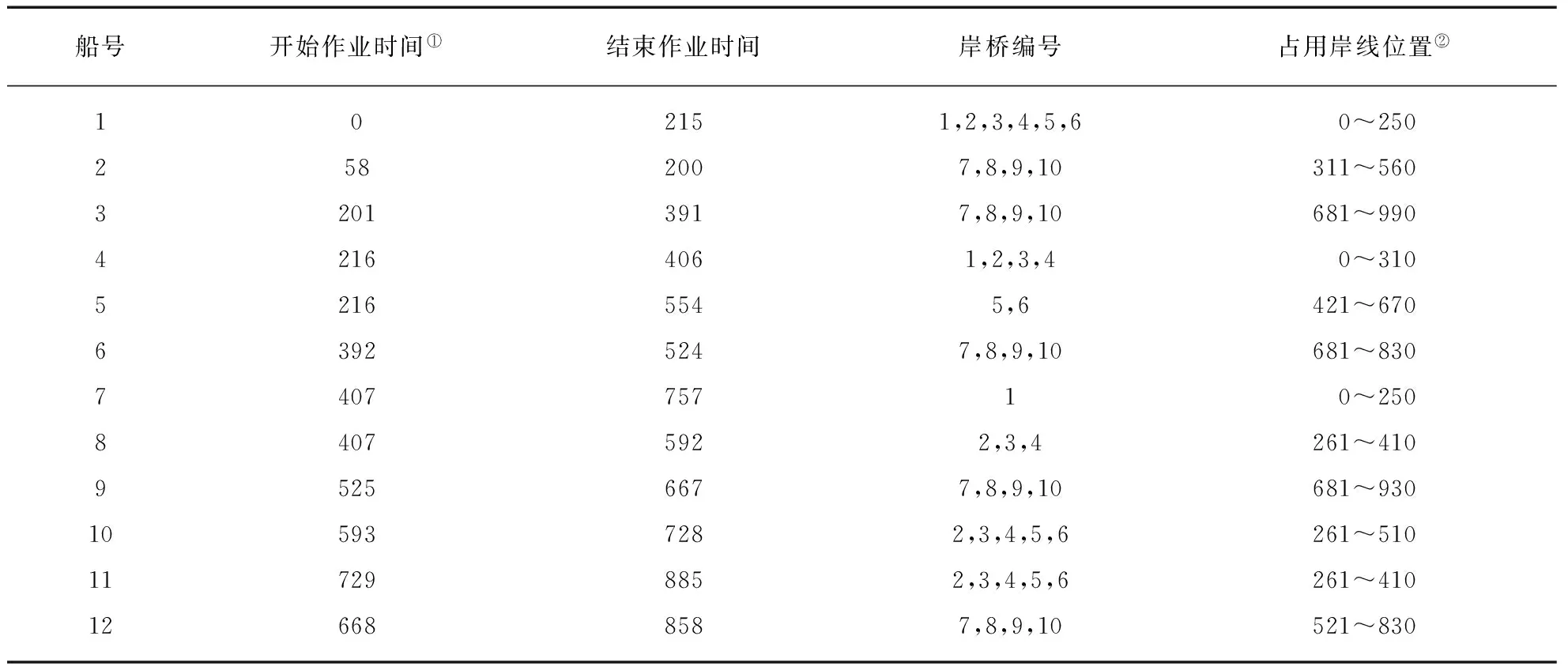
表3 船舶布局调度计划

注： ①这里的时间单位为min，表示每艘船舶作业时间在所有船舶整个作业时间中的位置；②0～250表示船舶占用岸线从0m到250m的位置停靠.

5 结 语

将连续泊位下的泊位调度和岸桥分配问题抽象为一种新的三维布局问题进行建模求解，同时利用求解布局问题中的吸引子法进行船舶资源块的布局.在算法实现中考虑了岸桥不能相互跨越工作、船舶停泊不能超过码头岸线长度限制这些因素.

基于吸引子的布局调度方法可以很好地提高港区的整体资源利用率，同时合理地利用泊位和岸线资源，不至于发生过于拥挤的情形、保留了安全间距，同时使得岸桥附近的集卡不会由于船舶的靠泊密度过高而发生拥堵等情形.下一步的研究可考虑船舶的吃水深度限制，使得模型的研究结果与实际情况更为接近.

[1] 高超峰,胡志华.岸桥并行作业效率约束下泊位与岸桥集成分派[J].重庆交通大学学报，2014，33(3): 72- 76.

[2] 杜卫华,黄有方,杨 斌,等.岸桥移动约束的连续泊位和岸桥集成调度[J].上海海事大学学报,2013，34(4): 43- 48.

[3] 杨春霞,王 诺.改进Memetic算法求解集装箱码头泊位岸桥调度问题[J].计算机工程与应用,2011，47(22): 233- 235.

[4] 董 盼,胡志华,陶 莎.基于岸桥成本分析的集装箱港口泊位和岸桥分配问题[J].大连海事大学学报,2013，39(2): 60- 64.

[5] 乐美龙,刘秀玲.基于泊位偏好与岸桥干扰的泊位和岸桥分配[J].运筹与管理,2014，23(1): 90- 100.

[6] 乐美龙,万艳雪.基于启发式算法的全泊位岸桥调度研究[J].科学技术与工程,2014，14(16): 304- 309.

[7] 杨春霞,王 诺,杨华龙.集装箱码头泊-岸桥分配耦合优化[J].计算机集成制造系统,2011，17(10): 2270- 2277.

[8] IMAI A, SUN X，NISHIMURA E,etal.Berth allocation in a container port: Using a continuous location space approach[J].TransportationResearchPartB, 2005，39(3): 199- 221.

[9] IMAI A, NISHIMURA E, PAPADIMITRIOU S. The dynamic berth allocation problem for a container port[J].TransportationResearchPartB, 2001，35(4): 401- 417.

[10] 王金敏,齐 杨.矩形布局问题吸引子法的研究[J].图形学报,2012，33(6): 38- 44.

Abstract： As berth and quay crane are the scarce resource of ports, a reasonable assignment of these resources is of great importance to the terminal operation efficiency. Both berth allocation problem and quay crane assignment problem were investigated. It mainly employs two research techniques, the abstraction of berth time, quay cranes, and berth into a rectangle evaluation block and the transformation of the whole berth problem into a new 3D rectangle packing model. Calculation results of this research showed that 3D rectangle packing model, compared with traditional modeling method and algorithm, has a better overall consideration of all kinds of resources in terminal. This model has obvious superiority and can improve the macro terminal efficiency significantly.

Keywords： wharf; assignment; attractive factor placement algorithm; 3D layout; berth

ASolutionofBerthandQuayCraneAllocationProblemontheBasisofAttractiveFactorPlacementAlgorithm

SI Yujun1,2，WENG Lingtao1，ZHENG Zonghao1，DUAN Guolin1

(1.SchoolofMechanicalEngineering,HebeiUniversityofTechnology,Tianjin300130,China；2.GeneralCargoTerminalofPortofCaofeidianGroupCO.,LTD,Tangshan063000,China)

U691.3

A

0427- 7104(2017)01- 0029- 05

2016- 01- 13

河北省自然科学基金(F2014202241)

司玉军(1981—)，男，博士研究生；段国林(1963—)，男，教授，博士生导师，通信联系人，glduan@hebut.edu.cn.