基于MWST+T-K2结构学习算法的贝叶斯分类器
赵高长,王 欣,2,张仲华,韩 苗,魏 嵬
(1. 西安科技大学 理学院,西安 710054;2. 养生堂有限公司,杭州 310007;3. 西安理工大学 计算机科学与工程学院,西安 710048)
基于MWST+T-K2结构学习算法的贝叶斯分类器
赵高长1,王 欣1,2,张仲华1,韩 苗1,魏 嵬3
(1. 西安科技大学 理学院,西安 710054;2. 养生堂有限公司,杭州 310007;3. 西安理工大学 计算机科学与工程学院,西安 710048)
针对K2算法在构建贝叶斯分类器时节点排序不同影响分类准确率的问题,提出了一种MWST+T- K2结构学习算法,运用Matlab软件的BNT工具箱构建了MWST+T- K2分类器,并经过NBC、TANC、MWST和MWST+T- K2分类器对UCI数据库的24个分类数据集进行分类检验.结果表明,对4种分类器在24个数据集上的分类水平进行整体与两两比较时,MWST+T- K2分类器的分类水平均最优;在小数据集上比较时,MWST+T- K2分类器的分类水平取得全局最优,未取得局部最优;在大数据集上比较时,未取得全局或局部最优,低于TANC的分类水平.所以,MWST+T- K2结构学习算法是一种适合构建小数据集贝叶斯分类器的方法.
贝叶斯网络; 贝叶斯分类器; MWST+T- K2算法; 分类检验
将贝叶斯网络(Bayesian network)[1]中代表类别的节点作为类节点,其余节点作为属性节点,贝叶斯网络就成为了贝叶斯分类器[2],其分类准确率受网络结构的影响.早期的朴素贝叶斯分类器(Navie Bayes Classifier, NBC)假定各属性节点相互独立,虽然在初期取得了一定的分类精度,但却并不适合一些研究领域[3].Friedman在NBC与最大加权生成树[4](Maximum Weight Spanning Tree, MWST)的基础上,利用条件互信息函数构造出树扩展的朴素贝叶斯分类器(Tree Augmented Navie Bayes Classifier, TANC),TANC在NBC的结构基础上允许各属性节点间构成一棵树,但规定各属性节点最多只能有一个非类父节点[5].这种结构充分应用了各属性节点间的信息,使TANC在一些数据集上的分类准确率有所提升[6].近年来一些学者提出使用K2算法构建贝叶斯分类器[7,8].K2算法在正确的节点排序下能够获得较好的网络结构,但是获得一个正确的节点排序是困难的[9].对该问题研究的进展比较缓慢,早期的研究学者使用遗传算法或启发式算法确定节点排序,在获得节点排序的同时往往伴随着局部最优、计算代价大等问题[10];2008年Chen 提出使用信息熵确定节点排序,使K2算法的结构学习获得了较好效果[11],同时简要提及使用该方法后K2分类器的性能[12];2014年Ko利用狄利克雷分布提出新的评分函数改进了Chen的方法,并通过实验表明所提方法在结构学习上的优势[13],但没有涉及分类问题.目前K2算法的节点排序问题仍未完善解决,这增加了使用K2算法构建贝叶斯分类器的难度.
MWST+T- K2算法是一种混合结构学习算法,“+T”代表选择MWST的正序排序.该算法首先利用MWST算法构建有向树,然后获得该有向树的正序排序(+T),之后将正序排序作为K2算法的节点排序,最后使用K2算法进行结构学习.MWST+T- K2算法可以保证类节点指向属性节点,这对构建贝叶斯分类器提供了条件,但也限制了其学习基准网络结构时的准确性.该算法构建基准网络时错误较多,所以一直没有得到多数研究学者的重视,只有极少数研究学者应用过该算法,但也没有分析该算法作为分类器使用时的理论依据和适用范围[14].
实验证明,MWST+T- K2算法是一种有效的使用K2算法构建贝叶斯分类器的方法.MWST+T- K2分类器与NBC、TANC和MWST分类器3种贝叶斯分类器相比,取得了实验数据集上的全局最优,并且在小数据集上取得了全局最优,但在大数据集上的表现不及TANC.
1 MWST+T- K2算法
MWST+T- K2算法主要由两个结构学习算法组成: MWST结构学习算法与K2结构学习算法.
MWST算法是一种早期的结构学习算法,其构建的MWST分类器为树形结构,具有结构简洁的特点,并且该算法在运行时只需要设定类节点.MWST算法首先计算出各节点变量间的联合概率分布,之后使用互信息函数来表示各节点间的相互依赖程度,对相应的边分配权重.互信息函数的计算方法如下:
(1)
在确定各边权重后,将权重从大到小排序,并从类节点出发添加权重最大的一条边,然后按照有向无环图(Directed Acyclic Graph, DAG)原则逐步添加剩余边中权重最大的边,直到建立一棵具有n-1条边的生成树.至此MWST算法结束,此时可以通过拓扑排序算法[15]获得该生成树的拓扑排序——正序(+T)或逆序(-T),这两个排序完全相反.使用K2算法建立贝叶斯分类器时需要保证类节点优先被使用,所以指定正序为K2算法的节点排序,再开始K2算法.
K2算法是一种经典的基于评分的结构学习算法[9].该算法的思想在于选择数据集D所构建网络结构中后验概率最大的网络结构,即有式(2):
(2)
其中:BS代表网络结构;πi代表节点Xi的父节点集合;qi代表节点Xi的父节点Xj的可能数目;ri代表节点Xi的类别数;Nijk代表节点Xi的父节点Xj中第k类的样本数目;Nij代表Xi的父节点Xj所有类别的样本数目之和.Nij与Nijk的关系为:
(3)
为了让式(2)的后验概率最大,只需要使式(2)中第2个内积最大即可.为此式(2)可以分解出式(4):

(4)
只要保证式(4)的值最大就能够保证式(2)的后验概率最大.但式(4)能够被计算的前提是满足3个假设: 1) 节点排序;2) 合适的父节点上限u;3) 当i≠j时,P(πi→xi)和P(πj→xj)边缘独立且先验概率能够被有效计算.实际上前两个假设都很难给定,这两个假设也是该算法在实现时需要设定的两个参数.
对第二个假设,K2算法自身使用了一个包含式(4)的贪心算法来解决父节点最大上限u的取值问题.因此u的取值对K2算法的结构学习结果只产生次要影响,并且u的取值也可以设置,最大值和默认值均为属性节点的个数,当设置值超过最大值时,将按照最大值来计算.对第一个假设,K2算法自身不能解决,而节点排序又对K2算法的结构学习结果产生主要影响,理论上要求前一个节点是后一个节点的父节点,才能获得较好的网络结构,这在实际中是难以实现的.采用MWST的正序排序作为K2算法的节点排序,可以弥补K2算法在节点排序上的不足,并且保证所建立的网络一定是贝叶斯分类器.在确定节点排序后,K2算法将按照节点排序和式(4)逐步添加边,直到最后一个节点时K2算法结束.至此MWST+T- K2算法结束,其伪代码可参看表1(见第50页).

表1 MWST+T- K2算法伪代码
2 实验准备
选用UCI(University of California Irvine)数据库的24个数据集作为实验数据集,在Matlab(版本号: 2014b)软件平台下,对NBC、TANC、MWST分类器和MWST+T- K2分类器进行分类准确率检验.各数据集概况见表2.选择Matlab软件作为实验平台的原因在于贝叶斯网络工具箱(Bayes Net Toolbox for Matlab, BNT)开源且开发已较为完善,具有从数据中进行结构学习、操作方式简单且灵活度高等特点.所有实验均在操作系统为XP系统(32位),CPU为i3 2120,内存容量为2G的硬件环境下进行.

表2 数据集概况
表2中,序号为1~15的数据集,Friedman曾做过NBC、TANC、MWST分类器及其他分类器的分类检验,并得到TANC对大多数数据集的适应性是最好的结论[16];序号为3,5,15~18的数据集,Cheng等曾做过NBC、TANC与其他分类器的分类检验,其结果可以借鉴[17];其余数据集为自选数据集.
表2中“分类数”代表类节点的分类数目.“属性节点”由“离散”、“连续”、“总计”3部分组成: “离散”代表该数据集属性节点中离散节点的个数;“连续”代表该数据集属性节点中连续节点的个数;“总计”代表该数据集属性节点的总个数.连续节点需要离散化处理,各数据集是否需要离散化可参见表2中的“离散化”.离散化方法选用熵最小的离散化方法,即Fayyad等的MDL(Minimum Description Length)算法[18].使用该离散化方法的原因: 1) 该方法能利用最小的数据压缩量刻画数据中的变化规律,同时避免过拟合现象;2) Friedman等同样对数据集使用了MDL算法,可说明BNT工具箱下NBC、TANC、MWST分类器分类结果的信度.数据离散化之前剔除了缺失项数据,并剔除了缺失项较多的节点.“检验方法”代表分类准确率检验的方法,依数据集大小分为两种方法.一种方法是适用于小数据集的“5折交叉验证”检验法[6],记为“CV- 5”;另一种方法是适用于大数据的“保留验证”检验法[19].表2中未使用“CV- 5”检验法的数据集都采用该方法,该方法一般要求训练数据的数量多于检验数据.
各数据集分别使用各自的检验方法重复检验100次,再取其平均值来评估该分类器在各数据集上的分类准确率,分类准确率误差则采用100次检验结果的标准差来表示.
3 实验结果及分析
3.1实验结果
4种贝叶斯分类器利用数据集“iris”构建的分类器结构如图1(见第52页)所示.
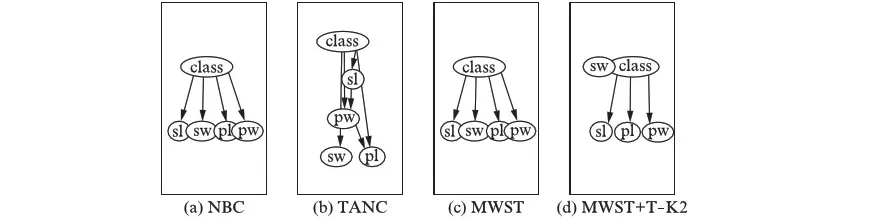
图1 Iris数据集构建的4种贝叶斯分类器Fig.1 Four Bayes classifiers learned for the dataset iris
图1从左往右依次是NBC、TANC、MWST和MWST+T- K2分类器,图中“class”代表类节点,“sl”、“sw”、“pl”、“pw”代表属性节点.从图1可以看出,MWST+T- K2分类器没有使用属性节点“sw”,而其他3种贝叶斯分类器使用了全部的属性节点.造成这一现象的原因在于K2算法的评分机制,对此可以参看伪代码.类似地,MWST+T- K2只在10个数据集上使用了全部的属性节点,而在14个数据集上只使用部分属性节点.这说明MWST+T- K2分类器在4种分类器中所使用的节点数量是最低的
4种贝叶斯分类器在24个数据集上的分类准确率见表3,并引用参考文献[16,17]的实验结果作为比较,相关数据也见表3.序号为3,5,15的数据集取参考文献[16]的结果.
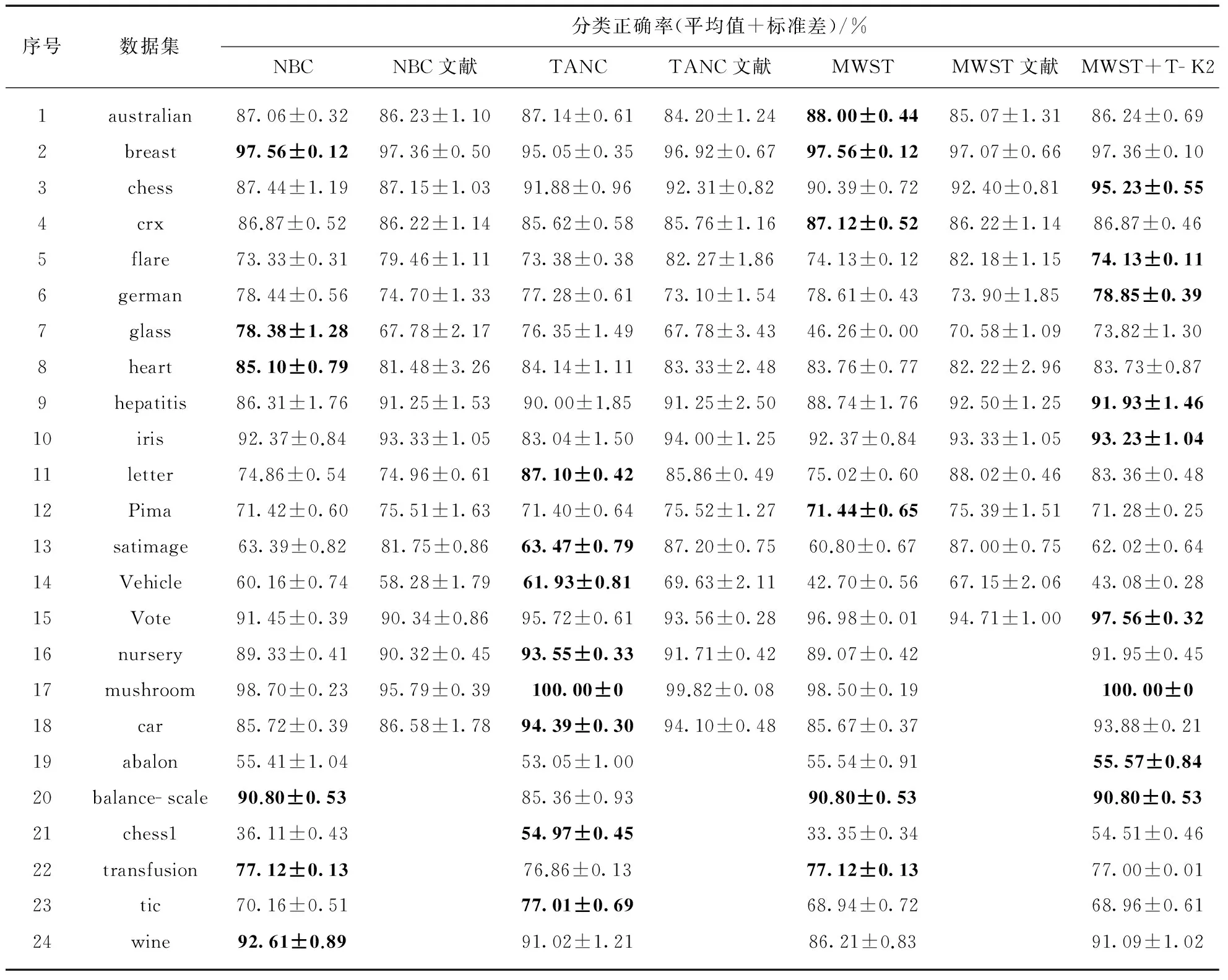
表3 4种贝叶斯分类器的分类准确率
注: 加黑的数字为该数据集的最优分类结果.
表3中,分类准确率只保留了两位小数.序号1~18的多数数据集分类准确率与参考文献[16,17]所得结果接近,说明表3中的分类准确率有一定信度,但也可以发现误差水平存在较大差异且在一些数据集上分类准确率也存在一定差异.造成差异的原因主要在于试验次数,同时也与硬件水平、实验平台等因素有关.
在24个数据集的分类结果中,NBC有6个最优分类结果,TANC有8个最优分类结果,MWST分类器有6个最优分类结果,MWST+T- K2分类器有9个最优分类结果.这说明MWST+T- K2分类器的分类水平具有一定优势,分别高出NBC 3个数据集,TANC 1个数据集,MWST分类器3个数据集.
3.2实验结果比较
将4种贝叶斯分类器的分类结果进行比较,绘制了MWST+T- K2分类器与其他3种分类器的分类错误率比较图,如图2所示.
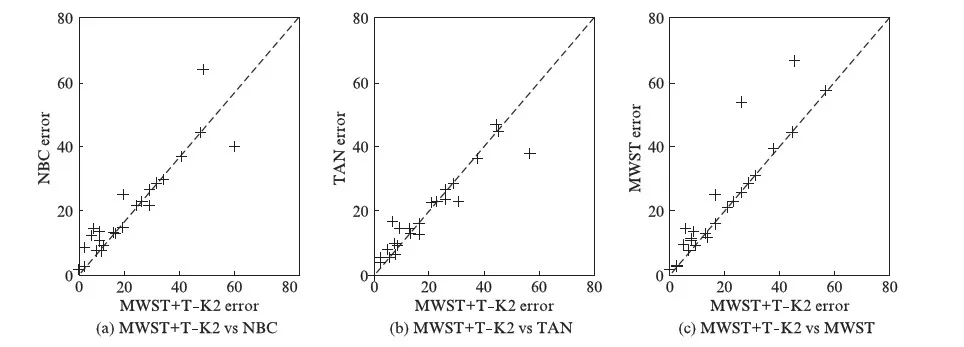
图2 4种贝叶斯分类器分类错误率比较Fig.2 Compared error rate of four Bayes classifiers
图2中,从左往右的3幅子图中,横轴坐标都为MWST+T- K2分类器的分类错误率,纵轴坐标则分别代表NBC、TANC、MWST分类器的分类错误率.结合表3数据与图2可以统计出,MWST+T- K2分类器在12个数据集上分类水平优于NBC,在2个数据集上两者分类水平相同,在10个数据集上分类水平劣于NBC;在12个数据集上分类水平优于TANC,在1个数据集上两者分类水平相同,在11个数据集上分类水平劣于TANC;在17个数据集上分类水平优于MWST分类器,在7个数据集上分类水平劣于MWST分类器.即单独比较MWST+T- K2分类器与其他3种分类器的分类水平时,MWST+T- K2分类器优于NBC 2个数据集,优于TANC 1个数据集,优于MWST分类器10个数据集.
进一步讨论4种贝叶斯分类器对数据集的适应性.根据表3数据绘制各分类器在各数据集上的误差棒,考虑到分类准确率误差采用单倍标准差的绘图效果并不理想,故这里采用5倍标准差进行绘图,绘图结果如图3(见第54页)所示.
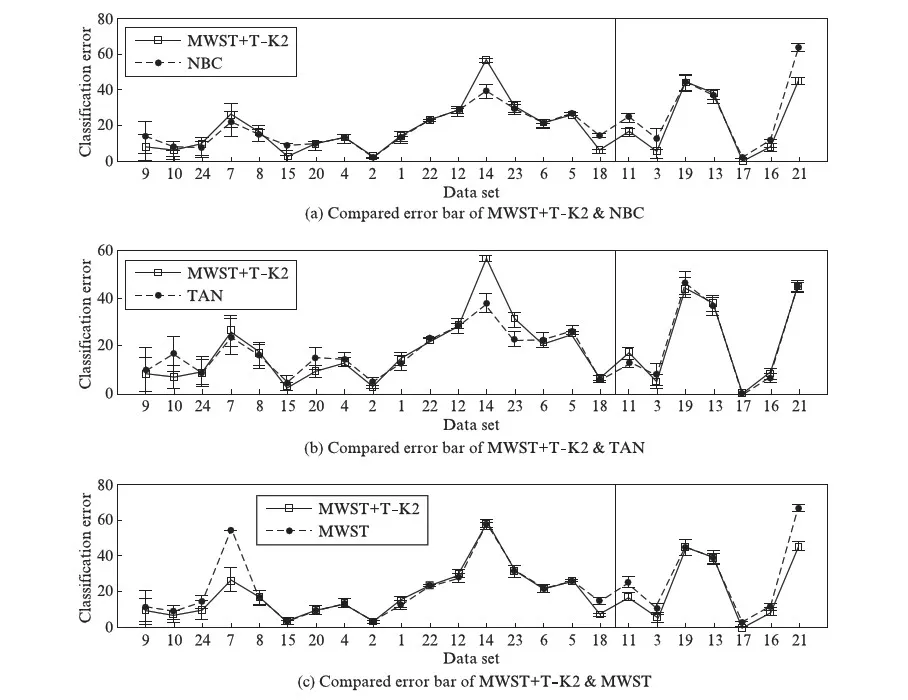
图3 4种贝叶斯分类器误差棒比较Fig.3 Compared error bar of four Bayes classifiers
图3的3幅子图,从上往下依次为MWST+T- K2分类器与NBC、TANC、MWST分类器的误差棒比较.横轴坐标代表各数据集序号,按分类检验方法的不同分类,即数据集的大小分类: 前17个数据集为小数据集,后7个数据集为大数据集,在图3中以竖线分开.
结合图3和表3数据统计出,在17个小数据集中,分类水平全局最优的分类器是NBC、MWST分类器与MWST+T- K2分类器,都在6个小数据集上取得了最高的分类准确率;TANC只在3个小数据集上取得了最高的分类准确率.单独比较小数据集的分类准确率时,MWST+T- K2分类器在6个数据集上分类水平优于NBC,在2个数据集上两者分类水平相同,在9个数据集上分类水平劣于NBC;在10个数据集上分类水平优于TANC,在7个数据集上分类水平劣于TANC;在10个数据集上分类水平优于MWST分类器,在1个数据集上两者分类水平相同,在6个数据集上分类水平劣于MWST.即MWST+T- K2分类器在小数据集上的分类水平低于NBC 3个数据集,各高出TANC 3个、MWST分类器4个数据集.
在7个大数据集中,最优分类器依次为TANC、MWST+T- K2分类器,各在5个和3个大数据集上取得了最高分类准确率,NBC和MWST分类器没有在任何大数据集上取得最高分类准确率.单独比较时,MWST+T- K2分类器在6个数据集上分类水平优于NBC,在1个数据集上的分类水平劣于NBC;在2个数据集上分类水平优于TANC,在1个数据集上两者分类水平相同,在4个数据集上分类水平劣于TANC;在所有的大数据集上分类水平都优于MWST分类器.即MWST+T- K2分类器在大数据集上低于TANC 2个数据集,高出NBC 5个数据集,高出MWST分类器7个数据集.
通过以上分析可知,MWST+T- K2分类器与NBC、TANC、MWST分类器在整体比较与两两比较时,均优于其他3种分类器;在小数据集上,其分类水平高于TANC和MWST分类器,低于NBC,但该分类器在小数据集全局上取得了最优,所以MWST+T- K2分类器是一种较为适合小数据集的分类器;但该分类器在大数据集上的分类水平虽高于NBC和MWST分类器,但低于TANC,且在全局上劣于TANC,所以MWST+T- K2分类器并不是一种理想的大数据集分类器.
4 结 语
本文提出了一种基于MWST+T- K2结构学习算法构建贝叶斯分类器的方法.实验证明,该算法是一种有效使用K2算法构建分类器的方式,并且所构建的MWST+T- K2分类器在UCI数据库的24个数据集中,分类准确率最高的数据集有9个,高于其他3种贝叶斯分类器;在两两比较分类准确率时占有较大的优势,优于NBC 2个数据集,优于TANC 1个数据集,优于MWST分类器10个数据集;在小数据集上的分类水平取得了全局最优,单独比较其与NBC的分类准确率时,虽然低于NBC 3个数据集,但仍不失为一种适合小数据集的贝叶斯分类器;在大数据集上的分类水平劣于TANC,虽然对NBC和MWST分类器有一定的优势,但却不是理想的大数据集分类器.同时该分类器能够使用最少的属性节点数目来得到一个不错的分类效果,这是其他3种贝叶斯分类器都不具备的.
MWST+T- K2分类器并不能取得大数据集上的全局最优或局部最优,故其适用范围受到了一定的限制.
感谢西安科技大学理学院张磊博士对本论文的帮助!
[1] 张连文,郭海鹏.贝叶斯网引论[M].北京: 科学出版社,2006.
[2] 洪海燕.基于贝叶斯分类器的简历筛选模型[J].计算机技术与发展,2012,22(7): 85- 87.
[3] DUDA R O, HART P E. Pattern classification and scene analysis[M]. New York: John Wiley & Sons, 1973.
[4] CHOW C K, LIU C N. Approximating discrete probability distributions with dependence trees[J].IEEETransactiononInformationTheory, 1968,14(3): 462- 467.
[5] 周颜君,王双成,王 辉.基于贝叶斯网络的分类器研究[J].东北师大学报(自然科学版),2003,35(2): 21- 27.
[6] FRIEDMAN N, GOLDSZMIDT M. Buliding classifiers using Bayesian network [C]∥Thirteenth Nation Conference on Artificial Intelligence. CA: AAAI Press, 1996: 1227- 1284.
[7] HRUSCHKA E R, EBECKEN N F. Towards efficient variables ordering for Bayesian networks classifier[J].Data&KnowledgeEngineering, 2007,63(2): 258- 269.
[8] LERNER B, MALKA R. Investigation of the K2 algorithm in learing Bayesian Network Classifiers[J].AppliedArtificialIntelligence, 2011,25(1): 74- 96.
[9] COOPER G F, HERSKOVITS E. A Bayesian method for the induction of probabilistic networks from data[J].MachineLearning, 1992,9(4): 309- 347.
[10] LARRAFIAGA P, KUIJPERS C M, MURGA T H,etal. Learning Bayesian network structures by searching for the best ordering with genetic algorithms[J].IEEETransactionsonSystems,Man,andCybernetics-pakta:SystemsandHumans, 1996,26(4): 487- 493.
[11] CHEN X, ANANTHA G, WANG X. An effective structure learning method for constructing gene networks[J].Bioinformatics, 2006,22(11): 1367- 1374.
[12] CHEN X, ANANTHA G, LIN X. Improving Bayesian network structure learning with mutual information- based node ordering in the K2 algorithm[J].IEEETransactionsonKnowledgeandDataEngineering, 2008,20(5): 628- 640.
[13] KO S, KIM D. An efficient node ordering method using the conditional frequency for the K2 algorithm[J].PatternRecognitionLetters, 2014,40(4): 81- 87.
[14] 王 强,彭思龙.基于贝叶斯网络模型的纹理分析及分类[J].计算机辅助设计与图形学学报,2007,19(12): 1564- 1568.
[15] 杨薇薇,王 方,秦 明,等.数据结构[M].北京: 清华大学出版社.2011.
[16] FRIEDMAN N, GEIGER D, GOLDSZMIDT M. Bayesian network classifiers[J].MachineLearning, 1997,29(2): 131- 163.
[17] CHENG J, GREINER R. Comparing Bayesian network classifiers[C]∥Proceedings of the 15th Conference on Uncertainty in Artificial Intelligence. San Francisco: Morgan Kaufmann, 1999: 101- 108.
[18] FAYYAD U, IRANI K. Multi- interval discretization of continuous- valued attributes for classification learning [C]∥Proceedings of Thirteenth International Joint Conference on Artificial Intelligence. CA: Morgan Kaufmann,1993: 1022- 1027.
[19] 程泽凯,林士敏,陆玉昌,等.基于Matlab的贝叶斯分类器实验平台MBNC[J].复旦学报(自然科学版),2004,43(5): 729- 732.
Abstract: The node ordering heavily affects the classified accuracy when one constructs Bayes classifier by K2 algorithm. Based on this problem, a kind of MWST+T- K2 structure learning algorithm is proposed, then this algorithm is applied to construct the MWST+T- K2 classifier through the BNT toolbox of MATLAB. At last, the classified test is carried out on the 24 data sets in the UCI database. The results imply that the classified level of the MWST+T- K2 classifier is globally optimal when the four classified levels is compared together or one is compared with anther on the 24 data sets; It is globally (not locally) optimal when the classifier level is compared with the others on all of the small data sets. The result, which is lower than the classified level of TANC, is neither globally nor locally optimal on all of the large data sets. Therefore, the proposed MWST+T- K2 structure learning algorithm is suitable to construct the Bayes classifier on small data sets.
Keywords: Bayesian network; Bayes classifier; MWST+T- K2 algorithm; classified test
BasedonMWST+T-K2AlgorithmtoBuildBayesClassifier
ZHAO Gaochang1, WANG Xin1,2, ZHANG Zhonghua1, HAN Miao1, WEI Wei3
(1.CollegeofSciences,Xi’anUniversityofScienceandTechnology,Xi’an710054,China;2.YangshengtangCO.,Ltd.,Hangzhou310007,China;3.SchoolofComputerScienceandEngineering,Xi’anUniversityofTechnology,Xi’an710048,China)
TP39
A
0427- 7104(2017)01- 0048- 09
2015- 12- 08
国家自然科学基金(41271518);陕西省教育厅科研计划项目(2013JK0583,14JK1474);陕西省自然科学基金(2016JM1025)
赵高长(1965—),男,教授;王 欣(1989—),男,硕士研究生,通信联系人,E- mail: 394315185@qq.com.

