LiFePO4锂离子动力电池内阻与放电倍率关系研究

罗红斌，邓林旺，冯天宇，吕 纯



LiFePO4锂离子动力电池内阻与放电倍率关系研究

罗红斌，邓林旺，冯天宇，吕 纯

（比亚迪汽车工业有限公司，广东深圳 518118）

研究锂离子动力电池内阻与放电倍率的关系可以改善电池管理系统（BMS）内阻模型的准确度和适应性，对提高电池状态如荷电状态（SOC）的估算精度具有巨大的意义和市场价值。本文采用二阶RC网络等效电路模型，通过不同倍率恒流放电和脉冲放电对25 A·h LiFePO4锂离子动力电池进行直流内阻（DCIR）和脉冲内阻（PDIR）表征，对不同荷电状态（SOC）下DCIR、PDIR0、PDIR1、PDIR2随放电倍率的变化规律进行拟合，得到DCIR、PDIR1、PDIR2、PDIRtot都非常符合双指数关系，PDIR0符合线性关系且几乎不变，并通过对比分析排除因温度造成内阻变化的可能。从固态电解质界面（SEI）生成速率与分解速率的化学平衡角度解释了DCIR、PDIR1、PDIR2、PDIRtot在低放电倍率时大可能是由于SEI分解速率小于生成速率，SEI与静置时的相似，电阻较大；反之，高放电倍率时小可能是由于SEI分解速率大于生成速率，SEI分解变薄并重新达到新的速率平衡，从而表现出较低的内阻。

LiFePO4；锂离子动力电池；内阻；放电倍率；二阶RC网络；电池管理系统（BMS）

锂离子动力电池具有功率密度高、内阻小的特点，适用于储能电站、混合动力汽车（hybrid electric vehicle，HEV）、插电式混合动力汽车（plug-in hybrid electric vehicle，PHEV）和纯电动汽车（electric vehicle，EV）等。LiFePO4动力电池因其安全性高、能量密度和功率密度较高、成本低、寿命长、环境友好等优点将在未来较长时间内作为储能电站和电动汽车（尤其是电动巴士）上的主力电池[1]。研究锂离子动力电池模型并将其应用于电池管理系统（battery management system，BMS）能更好地测量电池状态，充分发挥其性能。GOMEZ等[2]用电化学阻抗谱（electrochemical impedance spectroscopy，EIS）研究了锂聚合物电池的内阻随温度和SOC的变化规律，发现溶液和电荷转移电阻随温度的升高和SOC的降低而降低。SU等[3]研究了NCM三元锂离子电池的容量和内阻与温度和SOC变化路径的关系，发现容量衰减与SOC和温度变化路径都无关，而内阻增加与SOC变化路径有关，与温度变化路径无关。SCHMIDT等[4]使用高精度的数据采集仪，通过NCA三元锂离子电池脉冲放电的傅里叶变换得到内阻。但是他们都忽视了对内阻和电流变化规律的研究，而储能电站，特别是调频储能和电动汽车使用时是较为剧烈的变电流放电。因此，研究锂离子动力电池的内阻随放电倍率的变化规律有助于改善BMS内阻模型的准确度和适应性，可用于如卡尔曼滤波（Kalman Filter，KF）等多个电池状态估算算法中，提高电池状态估算精度，具有巨大的意义和市场价值。通常认为，电流倍率大会造成温度升高，使得离子迁移率和化学反应速率加快，从而内阻减小[2]。本文采用二阶RC网络等效电路模型（equivalent circuit model，ECM），通过不同倍率恒流放电和脉冲放电对25 A·h LiFePO4锂离子动力电池进行直流内阻（direct current internal resistance，DCIR）和脉冲内阻（pulse discharge internal resistance，PDIR）表征，可以排除因温度造成内阻变化的可能，并进一步总结出内阻随放电倍率的变化规律。

1 实 验

本文采用新威尔CT-4004-20V100A-NA测试仪对25 A·h LiFePO4方形锂离子动力电池（C20，BYD Company Limited）进行充放电和数据记录。充放电截止电压分别设为3.8 V和2.0 V。数据采样时间 0.1 s。进行测试前，首先在常温下以5 A对电池进行充电，以保证起始SOC态相同。对于恒流放电，使用0.2 C、0.5 C、1 C、2 C、5 C、10 C放电倍率分别进行恒流放电。对于脉冲放电，通过5 A恒流放电不同时间调节至所设各SOC态，进行0.2 C、0.5 C、1 C、1.5 C、2 C、3 C、4 C、6 C、8 C中某一倍率的脉冲放电，放电时长以固定放电容量0.75 A·h算得。每段脉冲放电结束后静置30 min，再以5 A恒流充电至所设SOC态，进行下一倍率脉冲放电。所有实验中，倍率与电流的对应关系为1 C=25 A，SOC都基于总容量25 A·h计算。

2 结果与讨论

2.1 电池直流内阻与放电倍率（DCIR～C-rate）的关系

图1(a)所示为不同倍率下恒流放电的电压容量曲线。采用工作电压和开路电压差值法，对比V-SOC曲线和OCV-SOC曲线，计算DCIR值，计算公式见式(1)

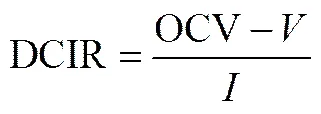
（a）

选取SOC=0.2、0.4、0.6、0.8时不同倍率的DCIR值，如图2所示。可以发现DCIR在小电流倍率时较大，而在大电流倍率时较小，变化规律符合如下指数关系

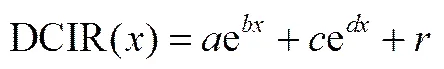
式中，、、、、为参数，为C-rate。拟合参数及误差如表1所示。各SOC下，相关度-square都非常接近1，说明该拟合方程可以解释超过99.9%的实验数据，能够很好地表达DCIR与放电倍率的变化规律。均方根误差（root mean square error，RMSE）在0.2左右，说明实验数据与拟合曲线波动较小，整体吻合度高。随SOC几乎不变，都在1 mΩ左右，对应二阶RC等效电路中的0，与后文脉冲放电测得的PDIR0值几乎相同。

表1 DCIR～C-rate按式(2)的拟合参数及误差

2.2 电池脉冲内阻与放电倍率（PDIR～C-rate）的关系

本文采用的二阶RC网络等效电路如图1(b)所示，各部分对应的物理意义如下：欧姆内阻0包括电池中电极、电解液、隔膜和终端导致的物理电阻。电化学极化内阻1主要指电极过程为电荷传递步骤控制时，由电极反应速率本身的延迟而引起的极化。其本质是电荷积累引起电极内电势及双电层电势差的变化而导致，也称为电荷转移电阻ct。浓度极化内阻2主要指电极过程由液相传质步骤控制时，电极所产生的极化。在电极表面附近的液层中，反应消耗的反应粒子得不到及时补充，或聚集在电极表面附近的产物不能及时扩散开，由此产生的偏离平衡电势的极化即为浓度极化[5-7]。为区别DCIR，二阶RC等效电路中的0、1、2分别记为PDIR0、PDIR1、PDIR2。

如图1(b)所示，在电池加载、卸载电流的起始瞬间，电池的电压响应会出现一个阶跃变化，而后缓慢变化。电流变化瞬间出现的电压跳变由电池欧姆内阻（0）引起，而之后电压缓慢变化则主要由电池的等效RC网络引起。因此，通过测量电流加载、卸载瞬间的电压变化即可得到电池欧姆内阻0，记为PDIR0。

脉冲放电开始时，RC网络开始充电，即零状态响应，其对应的电压可用式(3)～(5)描述。通过式(5)对脉冲放电过程中～曲线拟合，可得RC1、RC2、、。

（4）

（5）

（7）

由电容瞬态响应和RC网络基尔霍夫电流定律KCL分别可得式(8)和式(9)

（9）

（11）

同理可得，

因此，可由式(11)和式(12)得到RC网络中的1和2，即PDIR1和PDIR2。

图3所示为SOC=0.2、0.4、0.6、0.8时脉冲放电测得的PDIR0、PDIR1、PDIR2。PDIR0随SOC几乎不变，随C-rate缓慢上升，为1～1.5 mΩ，其值变化可能是由于采样时间0.1s间隔内，采样点的时间偏差引起的随C-rate有一些变化。按式(13)进行线性拟合的结果如表2所示。结合图3可以发现，由于实验数据在拟合直线附近随机波动，-square不是很接近1；另外RMSE并不大，这说明数据点都在拟合直线附近。PDIR0的波动主要由于随机误差造成。

按式(14)和式(15)对PDIR1和PDIR2进行双指数拟合，所得拟合参数及误差如表3、表4所示。不同SOC下，-square都非常接近1，且RMSE很小，说明双指数可以很好地描述PDIR1和PDIR2随C-rate的变化规律。PDIR1随C-rate变化的两个指数可能分别对应于电池正极负极上电化学反应造成的极化，同样，PDIR2随C-rate变化的两个指数可能分别对应于电池正极负极上粒子浓度差造成的极化。

（14）

（15）

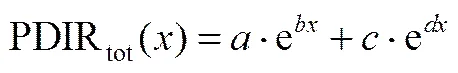
表2 PDIR0～C-rate按式(13)的拟合参数及误差

表3 PDIR1～C-rate按式(14)的拟合参数及误差

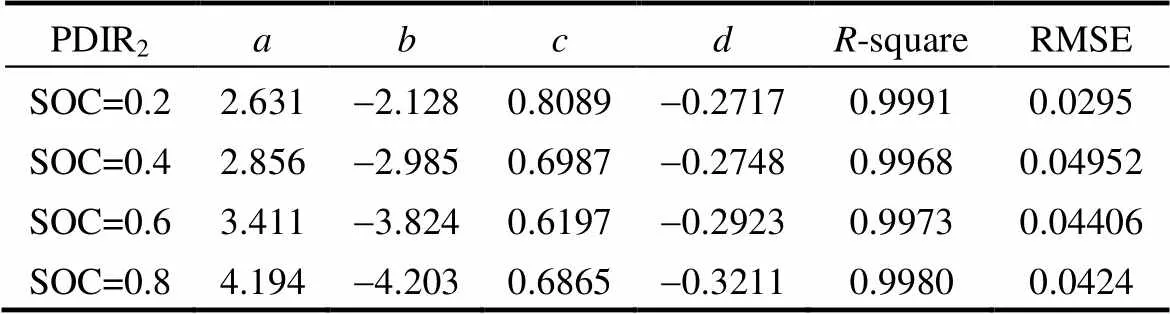
表4 PDIR2～C-rate按式(15)的拟合参数及误差

表5 PDIRtot～C-rate按式(16)的拟合参数及误差

2.3 电池直流内阻DCIR与脉冲内阻PDIR对比研究

图4为不同SOC、放电倍率下的DCIR、PDIR0、PDIR1、PDIR2的三维关系图。从图4(a)～4(c)可以直观地看到在不同SOC下DCIR、PDIR0、PDIR1、PDIR2都在低放电倍率时较大，在高放电倍率时较小，且符合指数关系。PDIR0在SOC～C-rate平面上是一个小斜率平面，变化很小。这些结论与前文3.1节和3.2节相同。

通常认为，电流倍率大会造成温度的升高，使得离子迁移率和化学反应速率加快，从而内阻减小[2]。但本文通过恒流放电和脉冲放电得到直流内阻DCIR和脉冲内阻PDIR，若内阻与C-rate关系是由于温度造成，则恒流放电时，DCIR应随SOC降低而减小，尤其对于中大倍率时应更是如此，但从图4和图5可以明显看到在某一放电倍率下，DCIR和PDIR在SOC为0.2～0.8时几乎不变，因此可以排除因温度造成内阻变化的可能。

另外，由式(17)算得的PDIRtot与DCIR几乎相等，这符合图1(b)中二阶RC网络等效电路对脉冲和恒流的响应，并且它们与放电倍率都符合前文所述相似的指数关系。

由于活性物质与电解液存在能级差，电极表面会自发进行氧化还原反应，形成固态电解质界面层（solid state interface，SEI），以钝化该反应继续发生，反应速率随该界面层厚度增加而减小，最终达到的平衡态厚度与电极电位有关，不同SOC态或充放电状态的电极电位不同，存在如式(17)所示的动态化学平衡[8]。SEI本质上是一层固态电解质，具有电子绝缘和锂离子导通的性质，阻止活性物质与电解液的反应持续发生。低倍率放电时，电极表面的SEI生成速率（钝化反应速率）大于SEI的分解速率，此时的SEI与静置时的SEI类似，电阻较大，钝化作用明显，因此体现出较大的内阻；较高倍率放电时，电极表面的SEI生成速率（钝化反应速率）小于SEI分解速率，SEI会变薄直至达到新的平衡态，因此体现出较小的内阻。化学反应速率与浓度等的关系一般是指数型变化，因而PDIR和DCIR与C-rate的关系也就体现出了这样的指数型变化。

3 结 论

LiFePO4锂离子动力电池的内阻与放电倍率的关系可以改善BMS内阻模型的精确度和适应性，对提高电池状态估算精度具有巨大的意义和市场价值。本文采用二阶RC网络等效电路模型，通过不同倍率恒流放电和脉冲放电对25A·h LiFePO4锂离子动力电池进行直流内阻DCIR和脉冲内阻PDIR表征，对不同SOC下DCIR、PDIR0、PDIR1、PDIR2随放电倍率的变化规律进行拟合，得到DCIR、PDIR1、PDIR2、PDIRtot都非常符合双指数关系，PDIR0符合线性关系且几乎不变，并通过对比分析排除因温度造成内阻变化的可能。DCIR与PDIRtot几乎相等，符合二阶RC网络等效电路对脉冲和恒流的响应。最后，从SEI生成速率与消耗速率的化学平衡角度解释了DCIR、PDIR1、PDIR2、PDIRtot在低放电倍率时大，而高放电倍率时小的原因。下一步可以加入温度因素，进一步研究温度、SOC、放电倍率对电池内阻的综合影响，并找到规律建立模型，还可将该研究方法推广至其它类型的锂离子电池（如三元电池）。

[1] DU J，OUYANG M，CHEN J. Prospects for Chinese electric vehicle technologies in 2016-2020: Ambition and rationality[J]. Energy, 2017, 120: 584-596.

[2] GOMEZ J, NELSON R, KALU E E, et al. Equivalent circuit model parameters of a high-power Li-ion battery: Thermal and state of charge effects[J]. Journal of Power Sources, 2011, 196(10): 4826-4831.

[3] SU L, ZHANG J, HUANG J, et al. Path dependence of lithium ion cells aging under storage conditions[J]. Journal of Power Sources, 2016, 315: 35-46.

[4] SCHMIDT J P, IVERS-TIFFÉE E. Pulse-fitting—A novel method for the evaluation of pulse measurements, demonstrated for the low frequency behavior of lithium-ion cells[J]. Journal of Power Sources, 2016, 315: 316-323.

[5] LUO W, LV C, WANG L, et al. Study on impedance model of Li-ion battery[J]. Industrial Electronics & Applications, 2011, 124(1): 1943-1947.

[6] LASIA A. Electrochemical impedance spectroscopy and its applications[J]. Modern Aspects of Electrochemistry, 2002, 32(4): 143-248.

[7] HU X, LI S, PENG H, et al. A comparative study of equivalent circuit models for Li-ion batteries[J]. Journal of Power Sources, 2012, 198: 359-367.

[8] FENG T, XU Y, ZHANG Z, et al. Low-cost Al2O3coating layer as a preformed SEI on natural graphite powder to improve coulombic efficiency and high-rate cycling stability of lithium-ion batteries[J]. ACS Appl. Mater. Interfaces, 2016, 8: 6512-6519.

The relationship between internal resistance and discharge rate of LiFePO4batteries

LUO Hongbin, DENG Linwang, FENG Tianyu, LV Chun

(BYD Auto Industry Company Limited, Shenzhen 518118, Guangdong, China)

This paper concerns the internal resistance as a function of discharge rate of Lithium-ion batteries. The aim of the work is to improve the accuracy and adaptiveness of internal resistance model for battery management system (BMS), which is of significance to the accurate prediction of the status of batteries such as the state of charge (SOC). We used a second order RC equivalent circuit model to analyze the direct current internal resistance (DCIR) and pulse discharge internal resistance (PDIR) with 25 A·h LiFePO4batteries under constant discharge and pulse discharge at various discharge rates. Data fittings were done on the DCIR, PDIR1, PDIR2and PDIRtotat various states of charge as a function of discharge rate and a good agreement was obtained with a double-exponential relationship, whereas a linear relationship held for the PDIR0. The analyses also suggested independence of the internal resistance change to the temperature effect. Based on the chemical equilibrium between the formation and decomposition of the solid electrolyte interface (SEI), we concluded that large DCIR, PDIR1, PDIR2and PDIRtotobserved at low discharge rates was likely to be due to low decomposition rate than the formation rate of the SEI with a high resistance, similar to the standby situation. On the other hand, a lower resistance at a higher discharge rate could be attributed to higher decomposition rates than the formation rates of the SEI, leading to a thinner SEI until a new equilibrium status was reached, and hence a reduced internal resistance.

LiFePO4; lithium-ion power battery; internal resistance; discharge rate; the second order RC equivalent circuit model; battery management system (BMS)

10.12028/j.issn.2095-4239.2017.0103

TM 911

A

2095-4239（2017）04-799-07

2017-06-14；

2017-06-16。

罗红斌（1966—），男，硕士，从事双模混合动力系统、纯电动汽车系统和核心零部件的研发、生产、管理以及调峰型/能量型储能系统、光伏发电系统、功率电气系统、智能化电池管理系统等的研发与生产工作，E-mail：luo.hongbin@byd.com；

邓林旺，研究方向为充电系统研发包括电池管理系统、车载DC、车载充电器、充电柜等，E-mail：deng.linwang@byd.com。