熔盐储罐冷却过程的瞬态分析
顾清之,张艳梅,关弘扬,张亚伟,段 洋,廖文俊
熔盐储罐冷却过程的瞬态分析
顾清之,张艳梅,关弘扬,张亚伟,段 洋,廖文俊
(上海电气集团股份有限公司中央研究院,上海 200070)
太阳能热发电易于和储热系统结合,通过储热系统,能够使电站平稳输出电力,因此是一种非常有前景的发电方式。熔盐储罐是储热系统中的重要设备,本工作建立了熔盐储罐冷却过程的模型,通过FLUENT计算,获得了熔盐储罐在不同情况下的散热量及熔盐储罐中熔盐温度下降的规律。计算发现,整个熔盐储罐中熔盐温度比较平均,但接近底部的熔盐发生了温度分层的现象;相同条件下,熔盐液位越高,熔盐发生凝固所需的时间越长,低温罐低液位(290 ℃,0.9 m)时所需凝固时间最短,只要3.8天开始凝固,19.3天后便完全凝固。
储热系统;熔盐;冷却;数值模拟;太阳能
太阳能热发电站使用太阳能来产生电力,是一种非常有前景的发电方式[1-2],其最具竞争力的优点就是易于和储热系统结合在一起,通过储热系统,电站发电可以摆脱太阳光不稳定带来的影响,使电站所发电更满足电网的需求[3-5]。目前,大部分光热电站使用熔盐显热储热系统,在阳光充足的时候,熔盐获得热量温度升高,储存在高温熔盐罐中,当阳光不足的时候,高温熔盐罐中的熔盐提供能量,使电站持续稳定的发电,熔盐温度变低,流入低温熔盐罐中[6-9]。在储热系统之中,熔盐储罐是关键设备之一,研究熔盐储罐冷却过程中的温度分布及散热机理有助于优化储罐设计及其运行调控。国内对大型熔盐储罐散热研究较少,崔武军等[10]通过实验测试小规模熔盐储罐中的温度分布,发现在加热过程中熔盐出现温度分层,在冷却过程中熔盐基本不发生分层现象。王康等[11]研究了导热油储罐的散热特性,发现储罐散热量随导热油降温而逐渐减小,提出了以储罐外壁表面平均温度为基础的热损失计算方法。国外对大型熔盐储罐的冷却过程已经有了一定的研究[12-16],美国的Solar Two是第一个投入到实际应用的大型熔盐储罐,PACHECO等[12]给出了Solar Two中熔盐储罐的散热量及测量方法,其中高温罐(565 ℃)的测量值为(102±21) kW,低温罐(290 ℃)的测量值为(44±6.6) kW,ZAVERSKY等[13]使用Modelica语言建立了熔盐储罐的热模型,计算了其在不同参考天时散热状况。RODRÍGUEZ等[14]用模块化面向对象的方法建立了熔盐储罐的散热模型,每个模块独立求解,计算发现储罐中边界地区的熔盐与核心区的熔盐的温差在2.5 K左右。PRIETO等[15]认为储热系统的散热是影响储热系统表现的重要因素,作者通过红外线摄像拍摄了储罐外壳的温度分布,发现设备支撑、储罐基础是影响储罐散热的重要因素。SUÁREZ等[16]使用文献值作为散热边界条件,在定热流密度的情况下计算了熔盐储罐避免熔盐发生凝固的最长待机时间,但实际上随着熔盐温度降低,储罐散热功率是在不断下降的,使用定热流密度会有一定误差,同时在凝固过程中熔盐会放出大量的潜热,不考虑这部分能量会极大缩短熔盐完全凝固所需时间。针对这两点问题,本文建立的模型中包括了储罐的保温结构,可以实时获得熔盐储罐的散热量,同时也将熔盐相变时的潜热考虑在内,最终获得了冷却过程中储罐内温度流场的分布及不同情况下储罐内熔盐凝固所需时间,模拟结果有助于优化储罐设计及其运行调控。
1 计算模型及计算方法
1.1 几何模型和网格划分
本文建立的物理模型参考Solar Two电站中实际使用的熔盐储罐,包括储罐的基本外形、储罐中熔盐的种类、液位、保温的种类及厚度都以文献[12]中的数据为准。储罐中所用熔盐的成分为60%(质量分数)NaNO3和40%(质量分数)KNO3,物性见表1[17]。

表1 熔盐的物性
储罐是平底的圆柱体,剖面结构如图1所示,储罐中存储了若干液位的熔盐,熔盐上方是空气(Solar Two没用氮气做保护气),高低温罐的直径都为11.6 m,高度分别为8.4 m和7.8 m,高温罐保温层的侧面及顶部分别有0.51 m及0.35 m矿物棉,低温罐保温层的侧面及顶部分别有0.28 m及0.2 m矿物棉,高低温罐的底部分别是0.3 m及0.41 m的泡沫玻璃板,在高温罐底部的泡沫玻璃板上还有0.15 m的耐火砖,由于容器内点的状态与周向无关,故可以选取圆柱截面的一半作为计算区域。在计算区域中熔盐及空气部分的网格划分采用了结构化网格,以高温罐高液位为例,该区域网格数量为 168×114,并且通过划分网格后的试算,调整边界层网格的厚度,使得靠近壁面的+的值接近于1,最终确定第一层网格的厚度调整为2 mm,边界层网格的增长率为1.2。
1.2 控制方程及求解方法
根据文献[13]以及本文试算得到的结果,储罐壁面与熔盐的温差在1~3 K之内,代入格拉晓夫数Gr中,其值大于1010,固熔盐区域处于湍流自然对流状态,采用模型。本文模拟过程中熔盐没有搅拌等外力推动,因此假设熔盐与空气的交界面法相速度为零。
熔盐区域的控制方程如下。
其连续性方程为
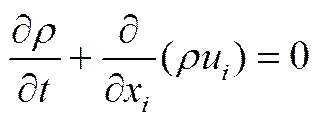
其动量方程为
(2)
上式中最后一项即雷诺应力项,需要求解雷诺应力项使方程封闭。本文采用FLUENT默认的Boussinesq假设建立雷诺应力和平均速度梯度的 关系
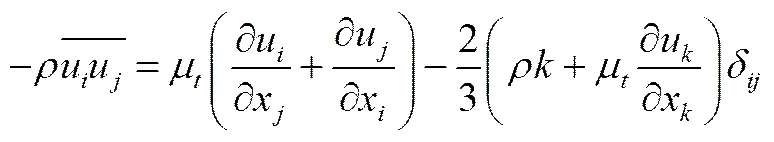
方程及方程如下
(4)
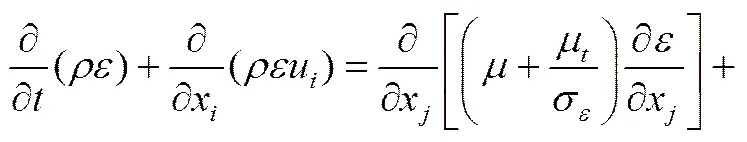
(5)
上述几式中,分别是动力黏度、流体密度、压强、重力加速度、流体速度,为湍动能,为湍流耗散率,δ为克罗内克算子,μ为涡黏性,G是由于平均速度梯度引起的湍动能的产生项,G是由于浮力引起的湍动能的产生项,1ε2ε3ε为经验常数。
熔盐的凝固包含了融化凝固模型,材料的总焓由显焓和潜热组成,其公式为
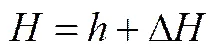
液相分数按如下方式定义
(7)
熔盐的潜热用表示
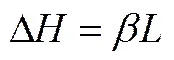
所以熔盐区域的能量方程可以表示为
(8)
其中为熔盐的导热系数,为源项。
本文模型的求解使用商业软件Ansys fluent 14.5,选用瞬态Axisymmetric,模型中的流态选用模型,并且打开壁面增强及浮升力,辐射模型选用P1,打开融化凝固模型,使用SIMPLE方法求解,压力离散格式选用PRESTO!,时间步长选择为5 s,残差收敛选用默认。
1.3 边界条件和初始条件
模型的边界条件如下。①图2中的左侧及上方即模型侧方及顶部采用对流换热边界条件,流体温度为外界环境温度,综合对流换热系数按国标[18]中的公式[,为平均风速]计算。②图2中的右侧即模型底部采用定壁温边界条件,温度为90 ℃。设置边界条件的理由如下:储罐底部的下面填充有保温材料,保温材料下有混凝土地基,在混凝土地基中设计了通风装置来保证混泥土不超过使用温度,参考文献[13]为90 ℃,故将最底部的混凝土的边界设置为定壁温90 ℃。在对储罐散热模拟的文献[13-14]中也做了类似假设。③图2中的下方即模型的中心采用轴对称边界条件。④内部壁面边界条件,采用无滑移流-固耦合传热边界。
在进行瞬态计算前,先将熔盐区域设为恒定温度,低温罐设定为290 ℃,高温罐设定为565 ℃,边界条件不变,然后进行稳态计算,通过这样的计算,储罐周围的保温材料、地基等有了储罐长期运行时的温度分布,以此稳态结果作为瞬态计算的初始值。
2 结果与讨论
2.1 模型验证及初始状态系统的散热量
在文献[12]中给出了两种测量熔盐储罐散热量的方法,分别为绝热法和冷却法,其中绝热法是通过调整储罐中的电加热功率,使熔盐温度保持不变,电加热功率与储罐散热量达到平衡,此时电加热的热功率就是储罐的散热量,冷却法是在一定时间中,关闭所有电加热,测量熔盐平均温度的降温速率,从而得到散热量,最终Solar Two实测散热量高温罐(565 ℃)为(102±21) kW,低温罐(290 ℃)的测量值为(44±6.6) kW。
参考文献[12]中数据,确定环境温度为20 ℃,风速为1 m/s,在此条件下,算得高低温罐在最高液位下散热量分别为101.5 kW及47.3 kW,在Solar Two测量值的误差范围之内。可认为模型基本正确。
高低温储罐在最高液位5.8 m和最低液位0.9 m中储罐内部各部分的散热量如下表2所示。由下表2可以看出液位对散热的影响,随着液位的降低,通过熔盐接触的那一部分湿周散发的热量在减小,然而另一方面,侧壁面与熔盐上表面辐射换热的表面积在增大,从而增大了这部分的散热量,同时从表中也可以发现,液位的高低对底部的散热量基本没有影响,综合这两方面考虑,液位降低略微减小了储热系统的散热量。Solar Two储热系统的储热量为106.5 MW·h[12],熔盐在储热系统高温罐中储存一天,其热量损失在2.3%左右。

表2 熔盐储罐各部分散热量
储热系统所处的环境温度对储热系统的散热量也有影响,下图3是高温罐总散热量随环境温度的变化规律,图中可见,储热系统的散热量随着温度的降低而增大,并且每单位温度下降增大的热量损失基本不变。
2.2 冷却过程中储罐内温度流场分布
熔盐的密度随着温度的升高而降低,因为重力的作用,通常温度高的熔盐处于储罐的上方,但是由于熔盐液面在剧烈向外散热(包括辐射与对流换热),顶部的熔盐冷却,温度降低密度变大,这部分熔盐会下沉,同时液面下方温度较高的熔盐会上升,这造成了熔盐上半部分有较强的对流发生,同理在靠近储罐侧边界也发生了类似的情况,图4低温罐高液位冷却两天后的流场分布,图5是同一时间部分区域的流线图。
但是在熔盐的下半部分,情况有所不同,接近底部的熔盐通过底部向外散热,温度降低,密度变大,由于重力的作用,这部分熔盐会继续停留在底部,这会导致底部熔盐的温度出现分层现象,越接近底部的熔盐温度越低。
图6是低温罐高液位冷却两天后储罐中的温度分布,图中可以明显的看到底部熔盐的温度出现分层现象,但是整个熔盐部分的温度还是比较平均的,温度最低的底部与最高的温度相差了大约3 K,由此可推测随着时间的推移,熔盐将在底部先发生凝固。
2.3 熔盐储罐中的温度随时间的变化规律
图7是高温罐低液位算例中各部分温度及熔盐液相分数随时间变化的曲线,由于熔盐储罐在不断向外散热,随着时间推移,熔盐的平均温度是在不断下降的,其中熔盐整体平均温度的下降经历了三个阶段,其中第一阶段为从开始到熔盐出现结晶即液相分数不为1时,此阶段熔盐温度不断下降,对外散热功率也在不断下降,所以熔盐温度下降的速率在不断减小。第二阶段为从熔盐开始结晶至熔盐完全凝固,此阶段情况比较复杂,由于熔盐凝固会放出大量潜热,熔盐温度下降的速率会大大降低,但在此阶段的后半段,熔盐已经凝固了大部分,能放出潜热的熔盐大量减少,熔盐温度下降的速率有所增大。第三阶段为从熔盐完全凝固至最终,此阶段与第一阶段相同,熔盐温度下降,散热功率下降,熔盐温度下降的速率不断减小。因此以定热流密度的方式来模拟熔盐冷却的瞬态过程是不够精确的。
在图7中还显示了空气、熔盐及交界面的温度随时间的变化规律,在高温阶段通常交界面的温度比熔盐整体温度低约3.4 ℃,空气又比交界面低约2.3 ℃,随着熔盐温度降低,交界面的辐射散热大量降低,空气与交界面间的温度差有所增加。其余算例也有类似规律。
2.4 凝固风险
储热系统是光热电站的重要组成部分,如果储罐中熔盐发生凝固,有可能造成设备损坏,再次解冻也将会非常困难,所以应当避免熔盐发生凝固,为了及时采取应对措施,对在不同工况下熔盐发生凝固的时间应当有所预计。表3是在不同条件下储罐中熔盐开始凝固及完全凝固所需的时间,从表中可以看到,低温罐低液位是最需要注意的,只要3.8天的停机熔盐就会开始凝固,而低温罐高液位则需要22.9天才开始凝固,液位高低对凝固时间有着很明显的影响,液位越高,熔盐凝固所需的时间越长,这是因为液位越高,储罐中熔盐越多,所储存的热量也越大,导致熔盐温降变慢。

表3 不同条件下熔盐储罐开始凝固及完全凝固所需时间
由于电站中常用的二元熔盐不是共晶体系,它的初晶温度和融化温度不是一个值,在这两个温度之间,熔盐处于固态和液态之间,图8是低温罐高液位在液相分数为40.1%时储罐中液相分布的云图,由图中可以发现,在储罐底部及侧边散热剧烈的地方,熔盐已经凝结成固体,在接近底部的区域,越接近底部液相分数越小。从图中也可以看出,熔盐的凝固是从底部与侧边的夹角开始的。
3 结 论
本文建立了熔盐储罐冷却过程的模型,采用数值模拟的方法研究了熔盐罐冷却过程中温度流场的分布以及熔盐温度液相分数随时间的变化规律,得出了以下结论。
(1)储罐中熔盐液位对储罐整体的散热量影响不大,液位降低略微减小了整体的散热量。
(2)储罐中熔盐的上半部分对流比较强烈,接近底部的熔盐发生了温度的分层,储罐中整体温度比较平均,在低温罐高液位冷却到2天时,熔盐的最高与最低温度相差3 ℃左右。
(3)储罐中熔盐温度的下降分为三个阶段:第一阶段为从开始到熔盐出现结晶即液相分数不为1时,熔盐温度下降的速率在不断减小;第二阶段为从熔盐开始结晶至熔盐完全凝固,熔盐温度下降的速率先降低后增大;第三阶段为从熔盐完全凝固至最终,此阶段与第一阶段相同,熔盐温度下降的速率不断减小。
(4)储罐中熔盐的凝固是从底部与侧边的夹角开始的,液位越高,熔盐凝固所需的时间越长,其中低温罐低液位(0.9 m)、高液位(5.8 m)分别在3.8天、22.9天后开始凝固,19.3天、107.3天后完全凝固,高温罐低液位(0.9 m)、高液位(5.8 m)分别在14.1天、91天后开始凝固,29.3天、177.5天后完全凝固。
[1] PARRADO C, MARZO A, FUENTEALBA E, et al. 2050 LCOE improvement using new molten salts for thermal energy storage in CSP plants[J]. Renewable and Sustainable Energy Reviews, 2016, 57: 505-514.
[2] 杨敏林, 杨晓西, 林汝谋. 太阳能热发电技术与系统[J]. 热能动力工程, 2008, 23(3): 221-228.
YANG M L, YANG X X, LIN R M. Solar energy-based thermal power generation technologies and their systems[J]. Journal of Engineering for Thermal Energy and Power, 2008, 23(3): 221-228.
[3] DINTER F, GONZALEZ D M. Operability, reliability and economic benefits of CSP with thermal energy storage: First year of operation of ANDASOL 3[J]. Energy Procedia, 2014, 49: 2472-2481.
[4] TORRAS S, PÉREZ-SEGARRA C D, RODRÍGUEZ I, et al. Parametric study of two-tank TES systems for CSP plants[J]. Energy Procedia, 2015, 69: 1049-1058.
[5] ARCE P, MEDRANO M, GIL A, et al. Overview of thermal energy storage (TES) potential energy savings and climate change mitigation in Spain and Europe[J]. Applied Energy, 2011, 88(8): 2764-2774.
[6] ANGELINI G, LUCCHINI A, MANZOLINI G. Comparison of thermocline molten salt storage performances to commercial two-tank configuration[J]. Energy Procedia, 2014, 49: 694-704.
[7] 张雅文. 太阳能电站双罐式熔盐蓄热系统的优化设计及研究[D]. 武汉: 华中科技大学, 2012.
ZHANG Y W. Study and optimal design on two-tank molten salt heat storage system in solar power plants[D]. Wuhan: Huazhong University of Science & Technology, 2012.
[8] PRIETO C, OSUNA R, FERNÁNDEZ A I, et al. Thermal storage in a MW scale. Molten salt solar thermal pilot facility: Plant description and commissioning experiences[J]. Renewable Energy, 2016, 99: 852-866.
[9] RODRÍGUEZ-GARCÍA M M, HERRADOR-MORENO M, MOYA E Z. Lessons learnt during the design, construction and start-up phase of a molten salt testing facility[J]. Applied Thermal Engineering, 2014, 62(2): 520-528.
[10] 崔武军, 吴玉庭, 熊亚选, 等. 低熔点熔盐蓄热罐内温度分布与散热损失实验[J]. 化工学报, 2014, 65(s1): 162-167.
CUI Wujun, WU Yuting, XIONG Yaxuan, et al. Temperature distribution and heat loss experiments of low melting point molten salt heat storage tank[J]. CIESC Journal, 2014, 65(s1): 162-167.
[11] 王康, 陆建峰, 丁静, 等. 槽式太阳能系统导热油储罐的散热特性[J]. 兰州理工大学学报, 2013, 39(4): 55-58.
WANG Kang, LU Jianfeng, DING Jing, et al. Heat-dissipation characteristics of storage tank for heat conducting oil in trough solar energy system[J]. Journal of Lanzhou University of Technology, 2013, 39(4): 55-58.
[12] PACHECO J E, BRADSHAW R W, DAWSON D B, et al. Final test and evaluation results from the Solar Two project[R]. Albuquerque: Sandia National Laboratories, 2002.
[13] ZAVERSKY F, GARCÍA-BARBERENA J, SÁNCHEZ M, et al. Transient molten salt two-tank thermal storage modeling for CSP performance simulations[J]. Solar Energy, 2013, 93: 294-311.
[14] RODRÍGUEZ I, PÉREZ-SEGARRA C D, LEHMKUHL O, et al. Modular object-oriented methodology for the resolution of molten salt storage tanks for CSP plants[J]. Applied Energy, 2013, 109: 402-414.
[15] PRIETO C, OSUNA R, FERNÁNDEZ A I, et al. Molten salt facilities, lessons learnt at pilot plant scale to guarantee commercial plants; heat losses evaluation and correction[J]. Renewable Energy, 2016, 94: 175-185.
[16] SUÁREZ C, IRANZO A, PINO F J, et al. Transient analysis of the cooling process of molten salt thermal storage tanks due to standby heat loss[J]. Applied Energy, 2015, 142: 56-65.
[17] FERRI R, CAMMI A, MAZZEI D. Molten salt mixture properties in RELAP5 code for thermodynamic solar applications[J]. International Journal of Thermal Sciences, 2008, 47(12): 1676-1687.
[18] 中华人民共和国国家质量监督检验检疫总局, 中华人民共和国建设部. 工业设备及管道绝热工程设计规范: GB 50264—97[S]. 北京: 中国标准出版社, 1997.
General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Ministry of Construction of the People's Republic of China. Design code for insulation engineering of industrial equipment and pipe: GB 50264—97[S]. Beijing: Standards Press of China, 1997.
Transient analyses of a molten salt heat storage tanks
,,,,,
(Central Academe, Shanghai Electric Group Company Limited, Shanghai 200070, China)
In this work, a computational fluid dynamics model is developed to analyze the cooling process of a molten salt tank during a standby period. The heat losses and temperature distribution under different conditions are obtained through the calculations. It is shown that the temperature distribution in the tank is mostly homogeneous, except for a temperature stratification closed to the bottom of the tank. Under the same conditions, the higher the level of molten salt, the longer time needed for the solidification of molten salt. For the cold tank at low molten salt level (290 ℃, 0.9 m), the estimated onset of solidification occurs in 3.8 days, and all the molten salt is solidified in 19.3 days.
thermal energy storage system; molten salt; cooling process; numerical simulation; solar energy
10.12028/j.issn.2095-4239.2017.0011
TK 02
A
2095-4239(2017)04-782-07
2017-02-08;
2017-03-31。
上海市重大技术装备研制专项(ZB-ZBYZ-02-14-1049),上海市产业转型升级发展专项资金(JJ-YJCX-01-16-0971)。
顾清之(1988—),男,硕士,工程师,主要研究方向为高温熔盐储热,E-mial:guqzh@shanghai-electric.com。

