欺骗式干扰下组网雷达优化布站方法分析与仿真

刘洁怡，张林让，赵珊珊，李 强，张 娟



欺骗式干扰下组网雷达优化布站方法分析与仿真

刘洁怡，张林让，赵珊珊，李 强，张 娟

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

针对组网雷达抗欺骗式干扰的资源优化问题，提出了一种优化布站方法。首先，对数据融合抗欺骗式干扰能力进行理论分析，给出组网雷达在空间不同位置被欺骗概率的理论值；利用理论分析结果，实现组网雷达被欺骗概率最小化和其覆盖范围最大化的联合优化布站，从而达到最优的资源利用方式。最后，通过仿真得到不同条件下的最优布站位置。

数据融合; 欺骗式干扰; 组网雷达; 优化布站

有源欺骗式干扰[1]主要应用于自卫式干扰和随队干扰中，可以利用雷达的匹配滤波增益，以较小功率达到较好的干扰效果，故其干扰技术及对抗策略成为学者研究的热点问题[2]。针对欺骗式干扰，单站雷达可利用发射信号优化[3]、运动学信息[4]和极化信息[5]，以及DRFM量化误差[6-7]对假目标进行鉴别，但单站雷达成本有限、视角单一，所能达到的抗干扰效能有限，对于逼真度较高的有源假目标，对抗效果不理想。

组网雷达可充分发挥多雷达数据融合的优势，利用真实目标的空间分布差异实现假目标的有效识别[8]。对于真目标，各节点雷达上产生的量测值转换到统一坐标系下，是位置信息重合、速度信息一致的。虽然由于雷达两量测误差的存在，可能不是完全相同的，也会位置相对“集中”，速度近似相同，称之为真实目标的空间相关性。然而，对于假目标，在干扰机没有准确获知所有节点雷达参数的情况下，无法对组网雷达进行协同欺骗，其位置相对“分散”，速度参数相差较大，即不具备空间相关性。利用真假目标空间相关性的差异，文献[9]提出一种自适应门限同源检验进行假目标鉴别的方法，是数据融合对抗欺骗式干扰的典型方法。

组网雷达中各雷达的相对位置会直接影响目标的空间相关性检验，因此，研究欺骗式干扰下组网雷达的优化布站有重要意义，通过优化布站可切实提高组网雷达抗欺骗式干扰的能力，降低组网雷达被欺骗概率。本文首先分析得到组网雷达被欺骗概率的理论值；在此基础上，研究被欺骗概率最小和雷达网覆盖范围最大下的联合优化布站问题；最后，对组网雷达的优化布站进行仿真分析。

1 数据融合抗干扰方法

本文主要讨论距离欺骗式干扰，即假目标位于雷达节点和真目标的延长线上[9]。假设目标和各雷达节点位于同一平面上，为场景论述方便，雷达分布及真假目标信息如图1所示。

组网雷达对各目标的量测是在各节点雷达为圆心的极坐标系中进行，在融合中心进行点迹关联之前，需要进行空间对准，即将各个组网雷达的量测值转换到统一的直角坐标系中[10]。对于节点雷达，其位置坐标为，设检测到目标的参数为，则变换到统一坐标系的坐标为：

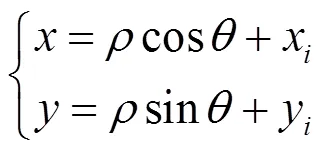
(2)

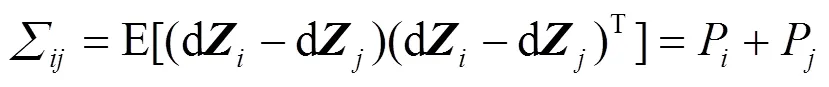
选择两雷达量测之间的马氏距离[11]为统计检验量：

在雷达个数大于2的情况下，每两部雷达均对假目标进行鉴别，然后对所有的判别结果进行融合处理，得到最终的鉴别结果。判决融合算法可以选择“取与”“取并”或利用K/M法则实现折中。一般采用最严格的“取与”法则进行判决融合(当且仅当所有融合结果均判断其为假目标，则该目标为假目标)。这种判决融合法则可最大限度地保证真实目标的正确鉴别概率。

2 欺骗式干扰对抗的理论分析

根据真实目标的空间相关性，可知两雷达对真实目标的状态估计值之间的差异服从零均值，协方差矩阵为的正态分布；而对于假目标，两雷达的状态估计值之间的差异服从均值为，协方差矩阵为的正态分布，如式(5)所示：

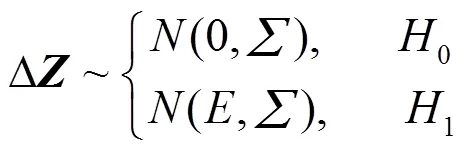
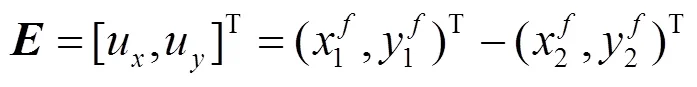
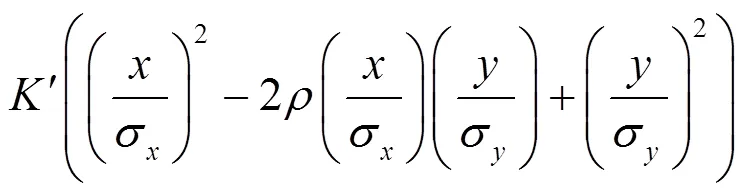
根据假设检验模型式(4)，可以看到数据融合方法对假目标的误判概率为：

将式(9)带入式(10)，可以得到：

(12)

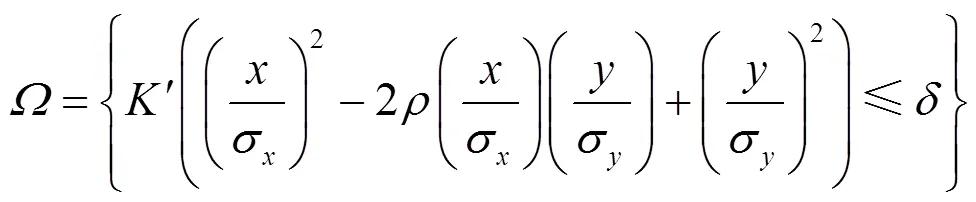
进一步化简得到：

(14)

(16)

若采用最严格的“取与”法则进行最终的判决融合，组网雷达被欺骗概率为：

3 组网雷达优化布站方法

根据第2节的理论分析可知，组网雷达被欺骗概率与两雷达相对目标的位置有关，所以通过对组网雷达中的节点雷达进行布站优化，可以使得其被欺骗概率最小。对组网雷达进行布站优化，首先需要选定探测区域，通过最小化该探测区域的被欺骗概率，完成雷达布站。同时，除了保证组网雷达的被欺骗概率最小这一优化目标外，还需要考虑最大化组网雷达的覆盖范围，因此组网雷达优化布站是一个联合优化问题。

根据第2节中得到的组网雷达被欺骗概率的理论值，可以得到最小化被欺骗概率的优化目标函数为：

最大化组网雷达的覆盖范围的目标函数可以写为：

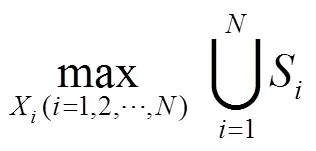
同时，组网雷达的布站位置也有一定的限制条件。首先，为保证多视角的优势和雷达接收到目标信号之间的非相干性，两雷达的距离不能太近，要大于一个门限值；其次，真假目标鉴别利用了组网雷达的冗余探测，则必须保证探测区域在雷达的探测范围内。

(20)

对于多目标优化问题，可以求得Pareto最优值，即对多个目标函数附以不同的权系数，合成一个标量目标函数，再进行优化求解。因此优化问题(20)的目标函数可以简化为：

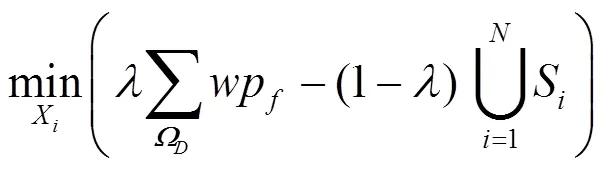
4 数值仿真实验

4.1 组网雷达被欺骗概率的仿真验证

以两部节点雷达为例，对组网雷达的被欺骗概率理论值进行仿真验证，设真实目标的位置坐标为(50,30) km，各节点雷达参数如表1所示。

表1 节点雷达参数表

设距离欺骗假目标的欺骗距离为300 m，进行多次Monto Carlo仿真实验，统计出该假目标的马氏距离的累积分布函数与理论分布函数式如图3所示。可以看到经验分布函数与理论分布函数非常近似。

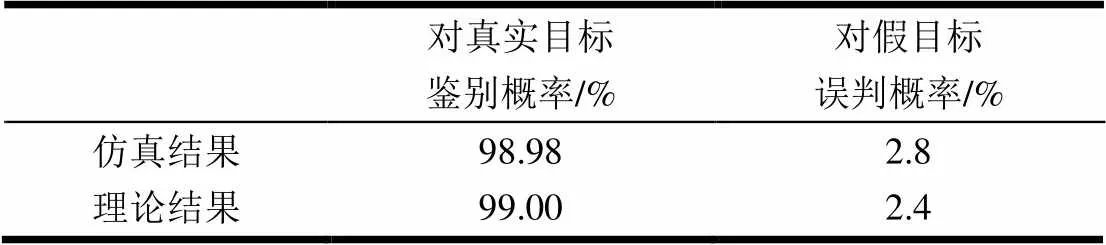
表2 节点雷达参数表

同时，对区间进行检测，轴的范围为-50～150 km，轴的范围为-20～110 km，可以得到整个区域的真目标的检测概率，及组网雷达被欺骗概率的仿真统计结果和理论结果，如图4所示。

a. 对真实目标鉴别概率的理论值

b. 对真实目标鉴别概率的统计值

c.组网雷达被欺骗概率的理论值

d. 组网雷达被欺骗概率的统计值

图4 组网雷达探测概率与检测概率区域变化图

从表2及图4的仿真结果可以看到，组网雷达被欺骗概率的理论值与仿真实验统计出来的概率十分接近，从而验证了本文对组网雷达被欺骗概率的理论分析是正确的。

4.2 组网雷达优化布站方法

以3部节点雷达组成的组网雷达为例，进行优化布站仿真分析，不失一般性，设探测区域为圆形区域，且等半径地分成5个子区域，每个子区域的加权系数由内到外依次增加：

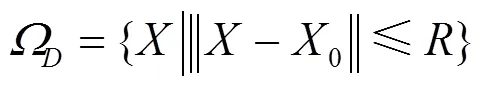
(23)

5 结束语

本文首先从理论上研究了数据融合对抗欺骗式干扰的能力，给出了组网雷达的被欺骗概率的理论值；并利用理论值研究了欺骗式干扰下组网雷达的优化布站问题，可以实现被欺骗概率最小和雷达网覆盖范围最大下的联合优化布站。本文的结果分析对组网雷达布站具有一定的理论指导意义。

[1] STAVROULAKIS P, FARSARIS N, XENOS T D. Anti-jamming transmitter independent radar networks[C]// International Conference on Signal Processing, Communications and Networking. Las Vegas, USA: IEEE, 2008: 269-273.

[2] LI Neng-jing, ZHANG Yi-ting. A survey of radar ECM and ECCM[J]. IEEE Trans on Aerospace and Electronic Systems, 1995, 31(3): 1110-1120.

[3] AKHTAR J. Orthogonal block coded ECCM schemes against repeat radar jammers[J]. IEEE Trans on Aerospace and Electronic Systems, 2009, 45(3): 1218-1226.

[4] RAO Bin, XIAO Shun-ping, WANG Xue-song, et al. Maximum likelihood approach to the estimation and discrimination of exoatmospheric active phantom tracks using motion features[J]. IEEE Trans on Aerospace and Electronic Systems, 2012, 48(1): 794-818.

[5] HUANG Can, CHEN Zhu-ming, DUAN Rui. Novel discrimination algorithm for deceptive jamming in polarimetric radar[C]//Proc of the 2012 International Conference on Information Technology and Software Engineering. Berlin: Springer, 2013.

[6] GRECO M, GINI F, FARINA A. Radar detection and classification of jamming signals belonging to a cone class[J]. IEEE Trans on Signal Processing, 2008, 56(5): 1984-1993.

[7] BANDIERA F, FARINA A, ORLANDO D, et al. Detection algorithms to discriminate between radar targets and ECM signals[J]. IEEE Trans on Signal Processing, 2010, 58(12): 5984-5993.

[8] GRIFFITHS H. Multistatic, MIMO and networked radar: the future of radar sensors?[C]//Proc of the 7th European Radar Conference. Paris: [s.n.], 2010: 81-84.

[9] 赵艳丽, 王雪松, 王国玉, 等. 多假目标欺骗干扰下组网雷达跟踪技术[J]. 电子学报, 2007, 35(3): 454-458.

ZHAO Yan-li, WANG Xue-song, WANG Guo-yu, et al. Tracking technique for radar network in the presence of multi-range-false-target deception jamming[J]. Acta Electronica Sinica, 2007, 35(3): 454-458.

[10] 赵艳丽, 陈永光, 蒙洁, 等. 分布式组网雷达抗多假目标欺骗干扰处理方法[J]. 电光与控制, 2011, 18(3): 25-30.

ZHAO Yan-li, CHEN Yong-guang, MENG Jie, et al. A data processing method against multi-false-target deception jamming for distributed radar network[J]. Electronics Optics & Control, 2011, 18(3): 25-30.

[11] 赵珊珊, 张林让, 周宇, 等. 组网雷达点迹信息融合抗假目标干扰方法[J]. 电子科技大学学报, 2014, 43(2): 207-211.

ZHAO Shan-shan, ZHANG Lin-rang, ZHOU Yu, et al. Measurement fusion method against false-target jamming for radar network[J]. Journal of University of Electronic Science and Technology of China, 2014, 43(2): 207-211.

编 辑 税 红

Analysis and Simulation of Optimal Deployment for Netted Radar under Deception Jamming

LIU Jie-yi, ZHANG Lin-rang, ZHAO Shan-shan, LI Qiang, and ZHANG Juan

(National Laboratory of Radar Signal Processing, Xidian University Xi’an 710071)

Netted radar has excellent performance for anti-jamming, especially for the deception jamming. According to the difference in spatial correlation, it can discriminate deceptive false targets by utilizing the method of data fusion. To solve the problem of optimal allocation of netted radar under deception jamming, we first analyze the anti-jamming ability of the fusion-based method in theory and obtain the theoretical expression for the cheated probability of netted radar. Based on the obtained theoretical expression, we propose an optimal deployment algorithm which can achieve the minimization of the cheated probability of netted radar and the maximization of its detection area. The simulations illustrate the locations of optimal deployment in different conditions.

data fusion; deception jamming; netted radar; optimal deployment

TN97

A

10.3969/j.issn.1001-0548.2017.04.006

2015-12-03 ；

2016-03-07

国家自然科学基金(61301281, 61001213, 61301285)

刘洁怡(1991-)，女，博士生，主要从事MIMO雷达、组网雷达抗干扰方面的研究.