多导脑电复杂度特征的谎言测试研究

高军峰，司慧芳，于晓琳，顾凌云



多导脑电复杂度特征的谎言测试研究

高军峰1, 4，司慧芳3，于晓琳2, 4，顾凌云5

(1. 中南民族大学生物医学工程学院 武汉 430074; 2. 武警警官学院信息工程系 成都 610213; 3. 认知科学国家民委重点实验室 武汉 430074; 4. 电子科技大学生命科学与技术学院 成都 610054; 5. 医学信息分析及肿瘤诊疗湖北省重点实验室 武汉 430074)

谎言测试在刑讯侦查和心理疾病治疗中具有重要意义。为了区分是否说谎，30名受试者被随机分为诚实和说谎两组，根据脑电信号的非线性特征——复杂性测度，对他们的12导联的脑电信号提取了KC复杂度、近似熵与样本熵3种复杂度特征，通过统计分析，用两类受试者具有显著差异的多导电极上的复杂度构建特征向量，最后使用支持向量机分类识别特征样本。研究发现：3种复杂度指标中，两类受试者的样本熵特征在更多电极上存在显著差异，由它们构建的特征向量的分类准确率最高，表明样本熵可以更有效地区分诚实和说谎两种不同脑认知状态下的脑电信号，该研究为基于脑电的测谎提供了一种新的途径。

复杂度; 脑电信号; 测谎; 非线性特征; 样本熵

测谎，是对谎言的鉴别活动。从心理学角度，测谎技术分为准绳问题测试法与犯罪情景测试法 (guilty knowledge technique, GKT)。后者主要是测试犯罪嫌疑人大脑中是否留有犯罪人应当留有的有关犯罪行为的记忆痕迹。该技术的心理基础是认知心理。P300是事件相关电位(event-related potential, ERP)[1]中的一种内源性成份，出现在刺激后300～800 ms时间窗口内的一个正向波[2]，主要反映了受试者的思维与决策过程。利用GKT技术进行测谎的原理是与案情相关的事物会引起罪犯进行更大的信息加工，从而引出高幅值ERP，而无辜者则相反。1987年，文献[3]首次利用事件相关电位进行测谎并获得实验上的成功。国内的作者也基于P300成分证明了测谎的可能性[4]。

研究表明，大脑神经元活动及其脑电(EEG)都表现为非线性动力学低维混沌特征[5]。近几年，脑电研究人员开始探索脑电信号的非线性特征——复杂度。复杂度的最初算法实现由文献[6]给出，称为算法复杂度，又称柯尔莫哥洛夫复杂度(kolmogorov complexity, KC)，简称KC复杂度。将KC复杂度用于脑电分析，可以刻画并区分不同状态下的脑电序列的复杂度[7]。近年来，研究人员又提出了其他复杂性测度。文献[8]引入了近似熵(approximate entropy, ApEn)理论，近似熵描述的是一维序列进行多维空间重构后，维数由增加至+1时产生新模式的可能性大小，利用该算法，只需少量数据就可得出稳定的数值。文献[9]提出了样本熵的概念，进一步提高了熵值算法的准确度。

目前为止，将脑电信号的复杂度特征用于谎言识别是否有效的研究还未见报道，基于GKT协议及脑电信号的P300成分，本文提出对说谎者和诚实者的脑电信号提取复杂度特征进行识别的方法。研究中，选用了广泛应用的3种典型的复杂度指标：KC复杂度、近似熵和样本熵，分别对两类受试者的多导脑电信号进行特征提取，最后使用分类器对两类受试者的特征样本进行分类，本研究的脑电信号处理基本流程如图1所示。

图1 提出方法的脑电信号处理基本流程

1 复杂度理论

本文选取3种典型复杂性测度算法，其中，KC 复杂度是把时间序列二值化为符号序列，然后对序列反复进行如下操作：每次添加一个元素构成一个检验子串，如果该子串在除去最后添加的那个元素之前所构成的序列中已经出现过，那么所构成的新序列的复杂度维持不变，并继续添加元素，直到上述情况未出现，复杂度增加1，继续添加元素并建立新的检验子串，如此反复进行，直到结束[10]。KC复杂度反映了给定序列随其长度的增长出现新模式的速率，即序列接近随机的程度。

Shannon熵理论用于复杂度刻画的理论基础即熵值越低，时间序列的自我相似性越高，反之则序列随机性越强，序列复杂度越高。样本熵与近似熵的最大区别就是无需进行自身模板匹配。本文仅对样本熵算法步骤描述如下：

1) 将信号表达为一个点的时间序列：

2) 构造一组维向量：

(2)

其中，

(4)

5) 增加维数至+1，重复上述步骤，计算：

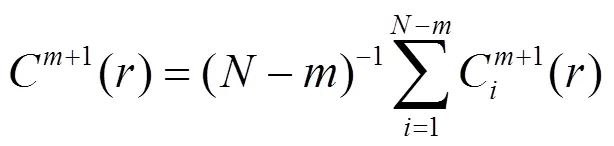
6) 样本熵定义为：

(7)

可见，样本熵的计算与参数和有关，值越大，计算量越大，耗费时间越长；值越小，噪声对结果的影响越显著，表示对序列自相似匹配程度要求越高。一般经验，对应=1 000时，可以设= 3，可以在0.1～0.25之间选择[11]。

2 实验过程与数据处理

2.1 受试者与测谎协议

受试者为30名身体健康的本科生，年龄为20～23岁，平均年龄22.3岁，右利手，无神经精神疾病及记忆障碍，视力正常。将他们随机分为无辜和说谎两组，每组各15名。标准三刺激模式作为测谎协议[12-14]，刺激信息为6张仿真珠宝图片，风格和材质相近，但颜色等细节特征存在显著差异。

实验要求说谎者“偷走”保险箱中的两个珠宝中的任意一个，作为探针刺激(Probe, P)，箱中另外一个作为靶刺激(Target, T)，其余珠宝作为无关刺激(Irrelevant, I)；诚实者认清保险箱中放入的唯一的一个珠宝，要求受试者看清该物品的细节信息，将其作为T刺激，从剩余的5个珠宝中任选一个作为P刺激，其余珠宝作为I刺激。实验过程中，屏幕上随机显示6张珠宝图片，要求受试者对看到的每张图片尽快做出反应，即要求诚实者全部“说真话”(见过该珠宝按鼠标左键，没见过该珠宝按鼠标右键)，而说谎者面对P刺激时，按右鼠标键，即回答没有见过，面对其余两类刺激时“说真话”。E-Prime2.0作为刺激软件。实验时每张图片随机出现50次，刺激间隔1.6 s，图片停留时间0.5 s。每次实验中，I、P和T刺激出现次数依次为120次、30次和30次。一次实验后休息5 min再重复上述实验5次。对行为学数据、响应时间及响应错误率，分别进行统计分析，显示两种受试者无显著差异。

2.2 数据预处理

采集电极如下：F3、Fz、F4、C3、Cz、C4、P3、Pz、P4、O1、Oz、O2，双侧乳突为参考电极，前额接地。眼电电极放在标准位置，Synamps放大器对信号进行放大，放大倍数500，通带频率为0.05～70 Hz，采样率500 Hz，各导联阻抗均小于3。

首先将采集的原始脑电用Neuroscan设备自带软件去除眼电，并去掉超过正负75 uv的信号段。然后在EEGLab工具箱[13]中对采集到的连续脑电信号进行分割，刺激前300 ms到刺激后1 300 ms作为一个Epoch。采用相干平均法，将每名受试者在各个电极上的每5个P刺激响应信号进行平均，称为少次刺激的平均ERP信号。

2.3 特征提取及统计分析

对各个导联上两类受试者的3种复杂度指标进行-test分析，以得到有显著差异的电极及对应的复杂度指标。

2.4 特征分类

对每一种复杂度指标，取出有显著差异的电极对上的两类受试者的复杂度值，组成特征向量，并送入到支持向量机[15-16]中分类。得出各个复杂度指标的测谎分类准确率。

3 实验结果与分析

3.1 预处理结果

图2为随机抽取的一名说谎者和一名诚实者在列举的6个极上的ERP波形，可以看出在这些电极上说谎者的ERP波形相对诚实者的ERP波形，P300特征都更为明显。

a. 说谎者

b. 诚实者

图2 两名受试者在6个电极上的少次平均ERP波形

3.2 统计分析

在正交试验的基础上,选择最优工艺配方对饮料品质进行验证试验,并进行感官评价,结果表明优化得到的黄刺玫果饮料配方最佳。

分别针对3种复杂度指标应用-test统计检验(由于多重检验，使用了Bonferroni校正，即< 0.01/12)，测试两类受试者在各个电极上是否存在显著差异。表1列举了12个电极上的两类受试者的3种复杂度指标的统计显著值。从表中可以看出，样本熵在更多的电极上存在显著差异。显著差异的电极有6个，分别是：P3、Pz、P4、C3、Cz、Oz。近似熵指标上达到显著差异的电极数为4个，分别是：P3、Pz、C3、C4。KC复杂度指标上达到显著差异的电极数为4个，分别是：F4、P4、C3、C4。

表1 在各个电极上的3种复杂度指标的统计分析(显著差异)

“**”代表两类受试者在该电极上的复杂度指标存在显著差异(<0.01/12)；“*”代表两类受试者在该电极上的复杂度指标存在显著差异(<0.05/12)；“○”代表受试者在该电极上的复杂度指标不存在显著差异。

针对每一种复杂度指标，构建分类模型：即将显著差异电极上的两类受试者的复杂度值取出，构成特征向量、对KC复杂度、近似熵及样本熵，3种分类模型的特征向量的维数分别为4、4及6。文中分别将3种分类模型称为KC复杂度模型、近似熵分类模型及样本熵分类模型。

对支持向量机分类器，首先取惩罚因子和RBF核函数(，Burges，1998)的参数通过下列网格=[2-5, 2-4, …, 28]和=[2-5, 2-4, …, 28](步长为2)进行训练，得到最佳参数。然后使用十则交叉验证，对每则的训练样本集进行训练，得出训练敏感度及特异度，记为：及。最后，将对应的测试样本集送入到训练好的分类器中，得出测试敏感度及特异度，记为：及，因此，通过十则交差验证，对于训练和测试，均可以得到10对敏感度及特异度，分别计算敏感度及特异度的均值及标准差(standard deviation, SD)，将它们显示在表2中。

表2可见，样本熵分类模型的训练及测试准确率均明显高于其他两种复杂度指标的分类模型(不同分类模型之间的准确率进行-test统计检验，均具有显著差异，< 0.01)；同时也发现样本熵与近似熵分类模型之间的准确率的差别较KC复杂度之间的准确率差别更小，即样本熵与近似熵分类模型的准确率更为接近；实验结果也发现KC复杂度模型相对于其他两种分类模型，标准差更大，即该复杂度指标产生的分类准确率波动性更大，推测应该是该复杂度指标相对于其他两种复杂度指标，更易受到噪声的干扰所致。通过计算，最后得到基于样本熵的分类模型的平均测试准确率为91.35%，高于基于KC复杂度模型的73.16%及近似熵分类模型的86.20%。

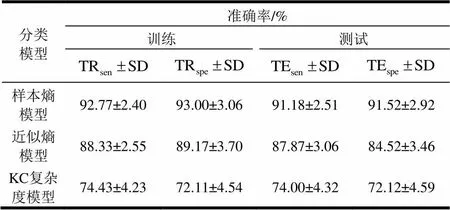
表2 3种分类模型的分类表现(准确率)

4 结束语

本文首次将非线性特征——复杂度指标用于测谎研究中，对谎言实验中的EEG信号进行复杂度分析，计算了脑电信号的KC复杂度、近似熵和样本熵3种指标值，通过统计分析，得到两类受试者具有显著差异的电极，分别建立特征向量进行分类。

样本熵是在近似熵的基础上发展起来的一种复杂度指标，样本熵拥有近似熵的抗噪、抗干扰的优点，避免了近似熵计算过程中出现的统计量不一致问题，这应该是本文中基于样本熵的测谎准确率高于近似熵的测谎准确率的原因之一。研究结果发现在3种复杂度指标中，样本熵的分类准确率最高，表明了该复杂度指标用于测谎的有效性。

研究中也尝试对单个电极的特征样本用于分类器，并将它们的最高准确率与多电极的特征联合的方式做了对比，均发现低于多电极的特征联合的准确率，此结果说明，多电极上的复杂度指标联合形成特征向量后，具有更强的分类能力，也即说明不同电极上的复杂度信息并非完全冗余，而是可以互补，可以提供更多的复杂度信息，对分类更有利，进而说明了提出方法中的多导脑电特征提取方案的优势。

由于本文研究过程中对原始脑电信号进行了5次平均进行降噪处理。因此，在实际测试过程中，可只对被试者使用约5次刺激进行测试，相对于目前广泛使用的BCD和BAD[12]等方法，本文提出的这种少次刺激的测谎方法更加简便，并降低了被测人员的疲劳程度，更有利于提高测谎准确率。

[1] Herrmann C S, Rach S, Vosskuhl J, et al. Time-frequency analysis of event-related potentials: a brief tutorial [J]. Brain Topography, 2014, 27(4): 438-450.

[2] Polich J. Attention, probability, and task demands as determinants of P300 latency from auditory stimuli[J]. Electroencephalography and clinical neurophysiology, 1986, 63(3): 251-259.

[3] Rosenfeld J P, Nasman V T, Whalen R, et al. Late vertex positivity in event-related potentials as a guilty knowledge indicator: a new method of lie detection[J]. International Journal of Neuroscience, 1987, 34(1-2): 125-129.

[4] 周亮, 杨文军, 廖四照, 等. P300用于模拟盗窃测谎的实验性研究[J]. 中国临床心理学杂志, 1999, 7(1): 31-33.

ZHOU Liang, YANG Wen-jun, LIAO Si-zhao, et al. Using P300 in the experimental study of mock criminal in lie detection[J]. Chinese Journal of Clinical Psychology, 1999, 7(1): 31-33.

[5] 徐琳, 许百华. 非线性动力学脑电信号分析方法的研究与应用[J]. 心理科学, 2005, 28(3): 761-763.

XU ling, XU Bai-hua. A research and application of the nonlinear analysis of EEG[J]. Psychological Science, 2005, 28(3): 761-763.

[6] Lempel A, Ziv J. On the complexity of finite sequences[J]. IEEE Transactions on Information Theory, 1976, 22(1): 75-81.

[7] Grandori F, Ravazzani P. Magnetic stimulation of the motor cortex--theoretical considerations[J]. IEEE Transactions on Biomedical Engineering, 1991, 38(2): 180-191.

[8] Pincus S M. Approximate entropy (ApEn) as a complexity measure[J]. Chaos, 1995, 5(1): 110-117.

[9] Richman J S, Moomaan J R. Physiological time series analysis using approximate entropy and sample entropy[J]. American Journal of Physiology: Heart & circulatory physiology, 2000, 278(61): 2039-2049.

[10] 孟丽艳, 赵晓宇, 姚力. 语言认知EEG非线性时间序列分析[J]. 北京师范大学学报(自然科学版), 2005, 41(6): 591-593.

Meng Li-yan, Zhao Xiao-yu, Yao Li. A time series analysis on language cognition EEG[J]. Journal of Beijing Normal University (natural science), 2005, 41(6): 591-593.

[11] 葛家怡, 周鹏, 赵欣, 等. 睡眠脑电时间序列的非线性样本熵研究[J]. 电子器件, 2008, 31(3): 972-975.

GE Jia-yi, ZHOU Peng, ZHAO Xin, et al. Research on sleep EEG time-series using nonlinear sample entropy[J]. Chinese journal of Electron Devices, 2008, 31(3): 972-975.

[12] ABOOTALEBI V, MORADI M H, KHALILZADEH M A. A new approach for EEG feature extraction in P300-based lie detection[J]. Computer Methods and Programs in Biomedicine, 2009, 94 (1): 48-57.

[13] Gao Jun-feng, Wang Zhao, Yang Yong, et al. A novel approach for lie detection based on F-score and extreme learning machine[J]. Plos One, 2013, 8(6): 1-12.

[14] Gao Jun-feng, Tian Hong-jun, Yang Yong, et al. A novel algorithm to enhanceP300 in single trials: Application to lie detection using F-score and SVM[J]. Plos One, 2014, 9(11): 1-15.

[15] 丁世飞, 齐丙娟, 谭红艳. 支持向量机理论与算法研究综述[J]. 电子科技大学学报, 2011, 40(1): 2-10.

DING Shi-fei, QI Bing-juan, TAN Hong-yan. An overview on theory and algorithm of support vector machines[J]. Journal of University of Electronic Science and Technology of China, 2011, 40(1): 2-10.

[16] 高军峰, 张文佳, 杨勇, 等. 基于P300和极限学习机的脑电测谎研究[J]. 电子科技大学学报, 2014(2): 301-305.

GAO Jun-feng, ZHANG Wen-jia, YANG Yong, et al. Lie detection study based on P300 and extreme learning machine[J]. Journal of University of Electronic Science and Technology of China, 2014(2): 301-305.

编 辑 蒋 晓

Study of Lie Detection Using Complexity Feature of Multichannel EEG

GAO Jun-feng1, 2, SI Hui-fang3, YU Xiao-lin2, 4, and GU Ling-yun5

(1. School of Biomedical Engineering, South-Central University for Nationalities Wuhan 430074; 2. Department of Information Engineering, Officers College of PAP Chengdu 610213; 3. Key Laboratory of Cognitive Science, State Ethnic Affairs Commission Wuhan 430074; 4. School of Life Science and Technology, University of Electronic Science and Technology of China Chengdu 610054; 5. Hubei Key Laboratory of Medical Information Analysis and Tumor Diagnosis & Treatment Wuhan 430074)

There is great significance in lie detection for the criminal investigation and psychological disease treatment. To distinguish lying, thirty subjects were divided into lying and telling-truth groups randomly and three groups of nonlinear features--complexity measures including Kolmogorov complexity, approximate entropy and sample entropy were extracted. By statistical analysis, the feature vector was constructed by using complexity on the muilti electrodes with significant difference of complexity values between the two groups of subjects. The support vector machine was used to classify and idendify feature samples. The study finds that there are more electrodes with significant difference of complexity values for the sample entropy, and the highest classification accuracy can be observed for the feature vector constructed from the sample entropy, compared with the other two featues. Experimental resutls indicate that sample entropy could be used to classify EEG signals in lying from EEG signals in telling-truth, which provides a new alternative for EEG-based lie detection method.

complexity; EEG; lie detection; nonlinear characteristics; sample entropy

R338

A

10.3969/j.issn.1001-0548.2017.04.026

2016-02-05；

2016-10-19

国家自然科学基金(81271659)；中国博士后基金(2014M552348, 2015M572465)；四川省科技厅基金(2015JY0222)；四川省教育厅项目(16ZA0449, 16ZA0452)

高军峰(1973-)，男，博士，副教授，主要从事生物医学信号处理与模式识别方面的研究.