稳定同伦群(Mζ(n,d)∧MBO＜n+1＞)挠元的计算

骆 芳

（云南师范大学数学学院，昆明 650500）

骆 芳

（云南师范大学数学学院，昆明 650500）

本文利用代数拓扑中的Adams谱序列、Thom谱以及B-配边理论等知识给出高维稳定同伦群挠元的计算，进而得出同伦群(Mζ(n,d)∧MBO＜n+1＞)的值。

高维同伦群；稳定同伦群；Adams谱序列；Thom谱、B-配边理论

1 背景介绍与预备知识

高维同伦群的计算一直是代数拓扑的难点与热点问题，1956年法国著名数学家J.P.Serre就因为球面同伦群的计算工作而获Fields奖。人们发现同伦群的自由部分可以用美国著名数学家，沃尔夫奖得主D.P. Sullivan提出的极小模型理论来解决。[1]但是挠元计算起来却极为困难。所以人们进而研究稳定同伦群来计算同伦群的挠元。起初，人们对群面稳定同伦群进行大量的研究， 在这方面我国的学者林金坤，王向军等做出了一定的贡献。[2]稳定同伦群的计算起源于代数几何中超曲面完全交的微分同肧分类问题。[3]近年来同伦群的计算在弦理论中也有着重要的应用，[4]所以同伦群的计算问题有着重要的理论与实际意义。

定义1.同伦群[5,6]：满足的所有同伦类组成的群 πn(M,x0)叫做同伦群.其中x0为拓扑空间M中固定的一个点。

由此可见，高维同伦群是基本群在高维的推广。由定义易知 (M, x)与x0的选择无关。所以为了方便起见，我们用记号πn(M)来代替 πn(M, x0)。

定义2.Thom谱[5,7]：如果复形序列计算已得到的一些结满足：＜∑Kn,Kn+1＞=＜Kn,ΩKn+1＞，则复形序列{Kn}以及由同伦等价映射所诱导的映射 (∑Kn→Kn+1)∈＜∑Kn,Kn+1＞ ，n∈称为Thom谱，Thom谱的逆向极限记为MKn。其中 ∑K=SK/(x0×[0,1]),x0∈K, SK 为K的双角锥，ΩK为K的路径空间。[4,5]

定义3.稳定同伦群[4,7]:对 于n连通的CW复形X，当i＜2n+1时，，我们把它们记为，称它为X的稳定同伦群。

下面我们将介绍Adams 谱序列,它是从计算球面稳定同伦群而产生和发展起来的工具。

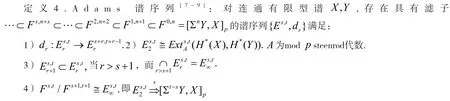
如果m维流形 M1,M2为m+1维流形W的边界，即M1M2=∂W,则称 配边于M2。所有m-维闭流形按配边等价关系组成一个群，我们称为配边群，记为:所有m维闭流形/配边关系。

定义5.B-配边：[10]如果 配边于M2，即 M1M2=∂W，且对于映射v∶W →BO以及 B→BO存在提升∶ W →B即满足下列交换图表：

则称M1B-配边于M2。满足条件的m维闭流形按B配边等价关系组成一个群，我们称为B配边群,记为Ωm(B)=:满足条件的m维闭流形/B配边关系。为以∞为底空间，以-(n+r+1)H⊕Hd1⊕…⊕ Hdr为丛空间的向量丛。其中H为P∞的典范复线丛，d1d2…dr=d。已有的结果表明无论 d1, d2,…dr怎么取 ，只要d1d2…dr=d，则是同构的，所以不失一般性，我们不妨记为ζ(n, d)。对于稳定同伦群的计算，已经有一些特殊的结果，比如的非挠元素可以由所确定，其中为空间Mζ(n, d)∧MBO＜n+1＞的第i个有理同调群[8,11]。

2 主要定理及其证明

为了得到定理1，我们首先证明一个引理

引理1：对于Mζ(n,d)∧MBO＜n +1＞的mod pAdams谱序列的滤子至少有vp(d)个，其中p为素数，d=∏pvp(d)。

证明：Mζ(n,d)∧MBO＜n+1＞的modpAdams谱序列可以写成如下形式

为了书写简便,记X=Mζ(n,d)∧MBO＜n +1＞。因为所以

结合上面的结论，下面我们证明定理1。

证明：易知Mζ(n,d)∧MBO＜n +1＞的modp谱序列有ℤ/p[ h0]-模结构。记，则E按ℤ /p[ h]-模可以写为E=TE⊕FE,其中FE为自由r0rrrr/p[ h0]-模，所以易知E∞的挠元属于TE∞。

由[14]可知，在(-1)-连通的Thom谱中，当。因为连通的Thom谱，所以结论成立。当p(p-1)≤n+1由s≥2且t-s≤2(p-1)·s-1以及上面的条件可得。所以当 p( p - 1) ＜n+ 1且的挠元为0。

3 结论

代数拓扑是一门十分活跃的数学分支。本文利用代数拓扑中的Adams谱序列、Thom谱以及B-配边理论等知识给出高维稳定同伦群挠元的计算，最后，我们得出此同伦群的挠元为0.结合

[1]D. Sullvan, Infinitesimal computations in topology, Inst. Hautes Etudes Sci. Publ. Math. 47 (1977), 269–331.

[2]J.K.Lin Detection of second periodicity families in stable homotopy of sphere, American J.of Math. (1990) 210-596.

[3]E. J. N. Looijenga, Isolated singular points on complete intersections, London Mathematical Society Lecture Note Series, 77, Cambridge: Cambridge University Press, (1984).

[4]A..Strominger, E.Witten, New Manifolds for Superstring Compactification, Commun.Math.Phys. 101 (1985) 341-361．

[5]A. Hatcher, Algebraic Topology, Cambridge University Press,(2002).

[6]诺维科夫等,潘养廉译,现代几何学:方法与应用(第二卷), 高等教育出版社,2007.

[3]林金坤,Adams谱序列与球面稳定同伦群,科学出版社,2007.

[7]R.Bott. The space of loops on a Lie group. Michigan Mathematical Journal, Vol.51958:35-61.

[8]R.M.Switzer, AlgebraicTopology—Homotopy and Homology,Classics in Mathematics, Springer,Berlin, 2002.

[9]Adams, J. Frank, On the structure and applications of the Steenrod algebra, Commentarii Mathematici Helvetici,1958:32(1): 180-214.

[10]R. E. Stong, Notes on cobordism theory, Princeton University Press, Princeton, N.J,1968.

[11]姜伯驹.同调轮.北京大学出版社,2007.

[12]W.Browder, Torsion in H-spaces, Annals of Math. 74,1961:24-51.

[13]V. Giambalvo, The mod p cohomology of BO(4k), Proc. A.M.S.20,1969:593-597.

[14]J. P. May and R. J. Milgram, The Bockstein and the Adams spectral sequences, Proc. A.M.S. 831981:128-130.

[责任编辑刘贵阳]

Abstract:In this paper, we use the knowledge of algebraic topology such as Adams spectral sequence, Thom spectrum and B-bordism theory to give the computation of torsion elements of higher homotopy group. And so we get the value of

Key words: Higher homotopy group; Stable homotopy group; Adams spectral sequence; Thom spectrum; B-bordism theory

Computation of Torsion Elements of Stable Homotopy Group(Mζ(n,d)∧MBO＜n +1＞)

LUO Fang
(Department of Mathematics ,Yunnan normal university, Kunming 650500, China)

O189.3+2

A

1008-9128（2017）05-0124-05

10.13963/j.cnki.hhuxb.2017.05.034

2016-12-27

骆芳（1987-），女，云南昭通人，硕士生，研究方向：非线性泛函分析以及代数拓扑等数学方面的研究。