锈蚀钢筋坑蚀因子概率分布模型研究

周牟瑶，魏 仁，李大望,2

(1.深圳大学 土木工程学院，广东 深圳 518060；2.深圳大学 广东省滨海土木工程耐久性重点实验室，广东 深圳 518060)

锈蚀钢筋坑蚀因子概率分布模型研究

周牟瑶1，魏 仁1，李大望1,2

(1.深圳大学 土木工程学院，广东 深圳 518060；2.深圳大学 广东省滨海土木工程耐久性重点实验室，广东 深圳 518060)

钢筋锈蚀后的形貌对于分析锈蚀钢筋力学性能退化规律及评定结构的安全性、预测其使用年限具有重要意义。锈坑作为锈蚀钢筋应力集中、延性降低的重要影响因素，其坑蚀因子概率分布是结构耐久性研究不可缺少的内容。对混凝土试块中50根通电加速锈蚀钢筋坑蚀因子的概率分布进行分析，探究不同锈蚀率、不同钢筋长度对钢筋坑蚀因子概率分布模型的影响。结果表明：混凝土中通电会引起锈蚀钢筋坑蚀因子概率分布模型服从对数正态分布，锈蚀率与钢筋长度不影响其概率分布类型，只影响坑蚀因子数值的均值和标准偏差。

锈蚀钢筋；3D扫描；坑蚀因子；概率分布

Abstract：The morphology of the corroded steel bar is of great significance to the analysis of the deterioration law of the mechanical properties of corroded rebar and the safety of the structure and the expected service life. As an important factor affecting the stress concentration and ductility reduction of corroded steel bars, the probability distribution of pitting corrosion factors is an indispensable element in the study of structural durability. In this paper, the probability distribution of 50 electric power accelerated corroded corrosion factors in concrete specimen is analyzed, and the influence of different corrosion rate and length of steel bar on the probability distribution model of the pitting corrosion factor is explored. The results show that the probability distribution model of pitting corrosion factor of corroded rebar will be caused by electric power in concrete, and the probability distribution type of corrosion rate and steel bar length are not affected, only the mean and standard deviation of pitting factor value are affected.

Keywords：corroded reinforcement; 3D scanning technology; pitting factor; probability distribution

钢筋混凝土结构在服役过程中，承载力的时变性可能受到各种因素的影响。钢筋混凝土结构受到恶劣环境侵蚀致使钢筋力学性能退化、混凝土截面开裂剥落、钢筋混凝土间黏结能力降低[1]，其中钢筋力学性能退化主要体现在钢筋截面面积减小、表面坑蚀等[2]导致的承载力降低。由于环境与混凝土材料、混凝土厚度空间分布的多相性，构件抗力衰减是个随机的过程，体现在锈蚀钢筋横截面面积分布不均匀、锈坑分布及锈坑深度不均匀等方面，可用平均锈蚀深度与最大坑蚀深度表示，前者表示了钢筋的全面锈蚀状况，后者则表示了钢筋局部锈蚀状况，建立起将全面锈蚀和局部锈蚀相联系的指标，为研究钢筋混凝土结构的可靠度及耐久性建立了基础。

坑蚀因子Rp为最大坑蚀深度Pmax与平均锈蚀深度Pav的比值[3]。现有文献对Pmax及坑蚀Rp的分布进行了研究，GAO Yanhong[4]对人工模拟环境下的锈蚀钢筋Pmax的概率分布进行研究得出Pmax服从正态分布的结论；Silvia Caprili[5]研究对象为模拟孔溶液中的锈蚀钢筋，得出结论为模拟孔溶液中Pmax服从Gamma分布；M. S. Darmawan[6]在加速锈蚀实验中获得的Pmax服从Gumbel分布。王青[7]通过对室外干湿循环下掺盐混凝土内的89根锈蚀钢筋进行分析，得Rp服从对数正态分布；马亚丽[8]通过分析混凝土板内锈蚀700 d的35根锈蚀钢筋，确定了Rp服从对数正态分布；Kashani[9]通过对混凝土试块中23根锈蚀钢筋进行研究，得出Rp服从对数正态分布的特征可以表示坑蚀沿着钢筋长度方向的非均匀性。由于环境与混凝土材料、混凝土厚度空间分布等条件的多相性，Pmax分布呈多样化，分布研究结果更加集中，大多服从对数正态分布。

既有的研究参数获取不精确致使数据源存在较大误差，或仅对数据进行了分布检验却并未探究分布的可能影响因素。传统测量方式如游标卡尺法、排水法[10]等虽能够获取Pmax及其他参数，且具有仪器操作简单、测试成本低廉等特点，但由于锈蚀钢筋形貌过于复杂，传统接触测量方法精度不高且耗费人力，仅适用于完好钢筋的形貌参数测量。3D扫描技术[11]则克服了这些缺点，其具有单次测量幅面大、测量精度高等多重优点。故采用3D扫描技术以获得锈蚀钢筋的精确参数，并建立Pmax与Pav比值Rp的分布模型，研究锈蚀率及钢筋长度对坑蚀因子概率分布类型的影响，为今后研究结构可靠度以及预期使用寿命建立了基础。

1 锈蚀试件及其坑蚀因子

1.1锈蚀试件

50根锈蚀钢筋来源于外加恒定电流的5个混凝土试块，其锈蚀过程由法拉第通电定律控制，电流密度为2.27 mA/cm2，HPB235光圆钢筋名义直径为14 mm，混凝土试件尺寸及钢筋布置方式如图1所示。为避免钢筋在通电锈蚀过程中两端发生更严重的锈蚀，故用电工胶布与环氧树脂处理端头各100 mm的区域，锈蚀区域仅为中间250 mm，见图2。达到预计通电锈蚀时长后，将试块破型并取出其内锈蚀钢筋，根据ASTM[12]进行清洗、后干燥处理直至锈蚀钢筋质量不再改变。

图1混凝土试件尺寸及钢筋布置图(单位：mm)图2钢筋端头保护示意图(单位：mm)

1.2坑蚀因子

对清洗后的锈蚀钢筋用3D扫描技术获取表观形貌模型后，利用MATLAB程序将锈蚀区段沿轴向以1 mm作为微段长度切分模型并提取所需参数。Rp计算式如式(1)所示：

Rp=Pmax/Pav

(1)

最大坑蚀深度Pmax计算方法为：

Pmax=r0-rmin

(2)

其中：r0为钢筋名义半径，rmin为锈蚀钢筋一个微段中外轮廓到形心的最小距离，如图3所示。

图3 钢筋锈蚀前后横截面轮廓示意图

平均锈蚀深度Pav计算公式为：

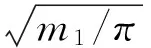
(3)

质量锈蚀率的计算式为：

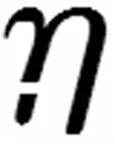
(4)

其中：m0表示未锈蚀钢筋的质量，m1表示锈蚀钢筋的平均质量。

2 坑蚀因子的概率分布

2.1假设检验

通过3D扫描技术获取的锈蚀钢筋形貌参数，经MATLAB处理后可计算坑蚀因子Rp，进而可通过假设检验来获得其分布。假设检验包括参数检验与非参数检验，非参数检验是在数据分布未知的情况下检验数据的分布情况，根据其适用范围及计算效率，可先采用Q-Q图获得Rp分布的粗略信息，然后用K-S检验来进一步完善信息。

2.1.1 Q-Q图检验

Q-Q图用于初步检验，能直观地辨别样本数据是否近似于某种特定分布[13]。绘制50根钢筋锈蚀区段长度为250 mm的Rp常见分布类型Q-Q图，如图4～图9所示。其中，图6～图9上大部分数据散点并未处在假定分布的直线上，而图4、图5数据点基本完全处于直线上，初步判断锈蚀钢筋坑蚀因子分布服从正态分布、对数正态分布。

图4正态分布Q-Q图图5对数正态分布Q-Q图图6 Weibull分布Q-Q图

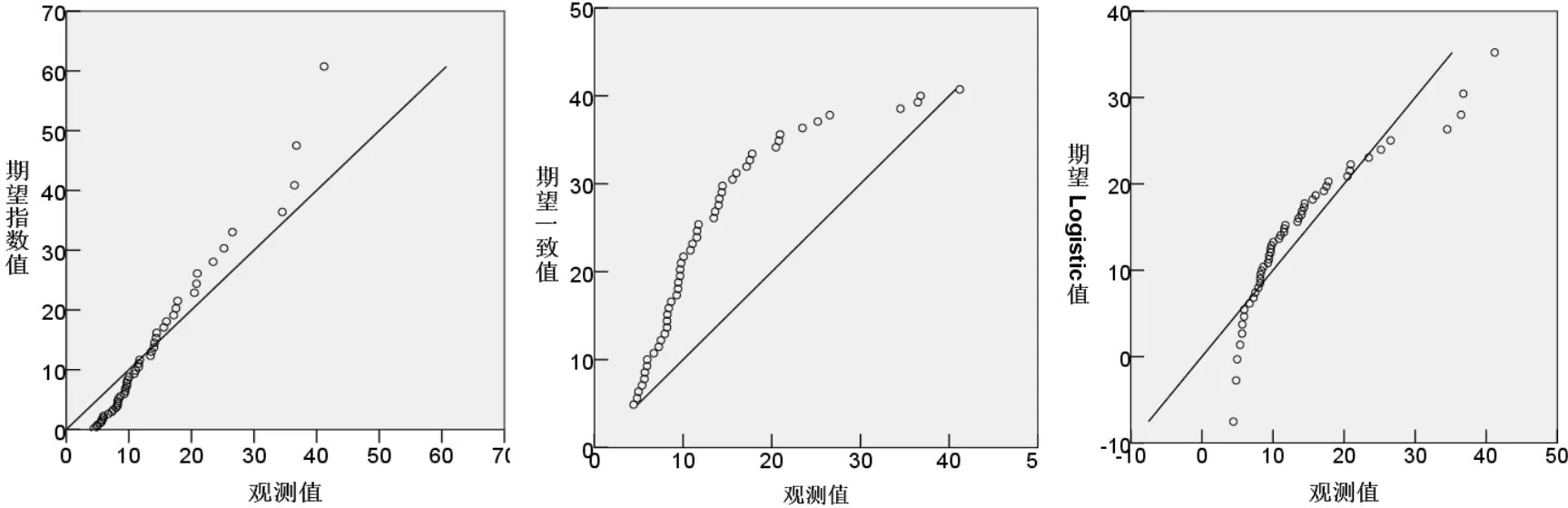
图7指数分布Q-Q图图8均匀分布Q-Q图图9 Logictic分布Q-Q图

2.1.2 K-S检验

K-S检验用于完善Q-Q图检验后的粗略信息，原假设H0：Rp总体服从正态分布，备择假设H1：Rp总体不服从正态分布，显著性水平α取0.05，D=0.174，Dcr=0.192，D0.089，故250 mm锈蚀长度的钢筋，其Rp概率分布取对数正态分布更优。

2.2锈蚀率对坑蚀因子概率分布的影响

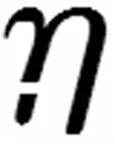
表1 不同锈蚀程度坑蚀因子概率分布表

由表1可得，锈蚀率对于Rp均值和标准偏差的影响较大，Rp服从对数正态分布的拟合度优于正态分布，钢筋的锈蚀程度与Rp分布类型无明显关系。

2.3钢筋长度对于坑蚀因子概率分布的影响

进一步考虑锈蚀钢筋长度对于Rp分布的影响，随机截取锈蚀钢筋上长度为150 mm的锈蚀区间，绘制150 mm长度与250 mm长度锈蚀钢筋Rp频率直方图，如图10、图11所示。

图10钢筋150 mm长度Rp频率直方图图11钢筋250 mm长度Rp频率直方图

K-S检验后可得150 mm长度的钢筋Rp符合对数正态分布。从统计学的角度分析，图10、图11数据的差距在于均值和标准偏差，锈蚀区段越长，Rp均值及标准偏差越大。结合锈坑沿钢筋长度方向分布位置及坑蚀深度随机性的特征可得，锈蚀钢筋局部锈蚀严重，随着锈蚀区段长度的增加，涵盖形貌参数的信息量越大，钢筋的长度值仅对于Rp均值及标准偏差有影响，对于坑蚀因子的概率分布模型并无影响，均符合对数正态分布。

3 结论

对混凝土试块中的钢筋进行通电加速锈蚀试验得到50根锈蚀钢筋，采用3D扫描技术精准获取锈蚀钢筋形貌参数，进而求得最大坑蚀深度、平均锈蚀深度及两者比值坑蚀因子Rp，并以Rp作为研究指标展开分析，探究锈蚀钢筋Rp分布及影响条件，得出以下结论：

(1) 3D扫描法作为锈蚀钢筋参数获取方法，可以快速获取钢筋高精度形貌参数，是分析锈蚀钢筋形貌特征的基础。

(2) 钢筋锈蚀程度分布不均，形貌复杂，Rp可综合表示全面锈蚀状况以及局部锈蚀状况。

(3) K-S检验方法检验不同锈蚀程度钢筋Rp的分布，在95%置信区间内，锈蚀率仅对Rp均值及标准偏差有影响，对分布并无影响，均以对数正态分布为最优分布。

(4) 采用K-S检验方法检验不同长度钢筋Rp分布，在95%置信区间内，钢筋长度仅对Rp均值及标准偏差有影响，对分布并无影响，均以对数正态分布为最优分布。

[1] 张威. 锈蚀钢筋表面特征的统计分析及其力学性能退化模型研究[D]. 西安: 西安建筑科技大学, 2013.

[3] Weiping Zhang, Binbin Zhou, Xianglin Gu. Probability distribution model for cross-sectional area of corroded reinforcing steel bars[J].Journal of Materials in Civil Engineering,2014,26(5):822-832.

[4] GAO Yanhong, WU Yaling, ZHOU Qiaoping. Study on the randomness of pitting corrosion depth of steel bar in concrete under the chlorine ion environment[J]. Journal of Natural Disasters,2014,23 (1) :221-228

[6] M.S.Darmawan. Pitting corrosion model for reinforced concrete structures in a chloride environment[J]. Magazine of Concrete Research,2010,62(2):91-101.

[7] 王青,徐港,卫军,等.混凝土中钢筋锈蚀深度比值的概率分布模型研究[J].工业建筑,2011,41(5):39-42.

[8] 马亚丽,张爱林.氯离子环境下钢筋最大腐蚀深度与平均腐蚀深度比值的概率分布研究[J].工业建筑,2005,35(12):11-14.

[9] Mohammad M.Kashani, Adam J.Crewe, Nicholas A.Alexander. Use of a 3D optical measurement technique for stochastic corrosion pattern analysis of reinforcing bars subjected to accelerated corrosion[J].Corrosion Science, 2013 , 73 (13) :208-221.

[10] 魏仁,官晓涛,李大望.卡尺法和排水法测试钢筋表观参数的有效性分析[J].河南城建学院学报,2016,25(4):1-5.

[11] 姜洪喜,任常愚,李海宝,等.光学三维形貌测量技术的分析和应用[J].黑龙江科技信息,2010(13):72-72.

[12] Standard practice for preparing, cleaning, and evaluating corrosion test Specimens[S].American Society For Testing and Materials G1-03,2004.

[13] 朱宁,赵肖肖,唐庆华.多元正态性检验三种方法的比较及SAS程序设计[J].苏州大学学报(自然科学版),2012,28(3):20-25.

[14] Linwen Yu, Raoul Francois, Vu Hiep Dang. Distribution of corrosion and pitting factor of steel in corroded RC beams[J].Construction and Building Materials,2015,95:384-392.

Studyonprobabilitydistributionmodelofpittingcorrosionfactorofcorrodedrebar

ZHOU Mu-yao1, WEI Ren1, LI Da-wang1，2

(1.SchoolofCivilEngineering,ShenzhenUniversity,Shenzhen518060,China; 2.KeylaboratoryofDurabilityofCivilEngineeringofGuangdongProvince,Shenzhen518060,China)

2017-06-11

国家自然科学基金项目(51278303)； 广东省教育厅重大项目(2014KZDXM051)

周牟瑶(1994—)，女，四川遂宁人，硕士研究生。

李大望(1963—)，男，河南洛阳人，教授，博士生导师。

1674-7046(2017)04-0019-05

10.14140/j.cnki.hncjxb.2017.04.004

TU511

A