沙粒粒径与含沙量对离心泵空化特性的影响

赵伟国，韩向东，李仁年，郑英杰，潘绪伟



沙粒粒径与含沙量对离心泵空化特性的影响

赵伟国，韩向东，李仁年，郑英杰，潘绪伟

（1. 兰州理工大学能源与动力工程学院，兰州 730050； 2. 甘肃省流体机械及系统重点实验室，兰州 730050）

为了研究沙粒粒径与含沙量对离心泵空化特性的影响，对含沙条件下与清水介质下离心泵内部空化流场进行数值计算。所采用沙粒粒径分别为0.005、0.010、0.015 mm，含沙量分别为0.5%、1.0%、1.5%。通过对清水介质外特性与平头圆柱空化流动进行数值计算并与试验结果相对比，验证算法的可靠性。计算结果表明：含沙量为1.0%时，随粒径逐渐增大，沙粒对空化的影响表现为先促进、后抑制；沙粒粒径为0.010 mm时，随含沙量不断增多，沙粒对空化的影响表现为先促进、后抑制。高压条件下，清水介质中无空化泡产生，含沙水流中均有少量空化泡产生。空化充分发展时，与清水介质相比，含沙水中空化泡分布表现为先增大、后接近、再变小。在沙粒磨蚀与空蚀的共同作用下，含沙水流条件下的扬程均低于清水介质下的扬程，且分别随粒径、含沙量的增加，逐渐减小。

离心泵；计算机仿真；模型；空化；沙粒粒径；含沙量

0 引 言

空化是液体内部由于局部压力降低而发生的汽化和液化现象，其本质是相变[1]。空化是复杂的多相流动，其发生和发展能诱发振动和噪声，使离心泵运行不稳定，严重影响整个系统的正常运行[2-6]；同时空化泡的溃灭对离心泵部件表面材料会形成巨大破坏[7-8]，导致其性能急剧下降。空化的产生与压力分布、流速等多种因素[9]相关，同时亦受介质因素[10]的影响。自然界的河流或多或少的含有悬浮泥沙与固体颗粒，以黄河干流为例，年平均输沙量达16.4亿t，多年平均含沙量为37.5 kg/m3[11]。运行在含沙水流中的离心泵,除遭受磨蚀破坏作用，由于沙粒的影响，其空化特性与清水介质下的空化特性相比，存在明显不同。

对含沙水流空化，许多学者都进行了研究。常近时等[12-15]通过试验得到实测水样中，随含沙量的增加，初生空化压力和临界空化压力均近似呈线性增加。Huang Si等[16-20]通过试验研究了固体颗粒含沙量、粒径、硬度等因素对空蚀破坏程度的影响。Poulain等[21-22]建立了空化泡与球形颗粒之间的相互作用模式。Madadnia等[23-24]研究表明：含沙水流条件下，空蚀与磨蚀的联合破坏作用均高于空蚀或磨蚀的单独作用。Bostjan等[25]通过水洞研究了不同固体颗粒含沙量对水翼空化发展的影响并得到相应工况下水动力与扭矩的变化特性。Zhao Weiguo[26]通过改变沙粒粒径与含沙量，研究了沙粒对喷嘴空化影响的规律。查阅相关文献可知，考虑粒径与含沙量对离心泵空化特性影响的研究并不多见。

本文基于数值方法，采用Mixture模型、RNG-湍流模型和-空化模型，对不同粒径与含沙量下的沙粒对离心泵空化特性的影响进行研究。依据黄河兰州段沙粒中值粒径分布特点，粒径分别取为0.005、0.010、0.015 mm；含沙量分别取0.5%、1.0%、1.5%。

1 数值算法

1.1 控制方程

含沙水空化流动中，沙粒作拟流体处理，混合相连续性方程、动量方程、体积分数输运方程如下所示。

式中u、u（，为1，2，3）为混合相速度，m/s；m为混合相密度，kg/m³，m=ll+ss+vv其中l为液相密度，kg/m³，v为汽相密度，kg/m³，s为沙粒相密度，kg/m³，l为液相体积分数，v为汽相体积分数，s为沙粒相体积分数。m为混合相黏度，kg/m·s，m=ll+vv+ss，其中l为液相黏度，kg/m·s，v为汽相黏度，kg/m·s，s为沙粒相黏度，kg/m·s；x、x（，为1，2，3）为笛卡尔坐标系坐标；为当地压力，Pa；为时间，s；+为蒸发源项；-为凝结源项。

1.2 湍流模型

采用RNG-湍流模型[27]对方程进行封闭，此模型充分考虑了旋转效应，有效提高了旋转流动的计算精度。其方程为

式中为湍动能，m2/s2；为湍流耗散率，m2/s3；t为湍动黏度，kg/m·s；k为由于平均速度梯度引起的湍动能产生项；1ε、2ε为经验常数；α，α分别为湍动能和耗散率的有效普朗特数的倒数，其值均为1.39；C为经验常数，值为0.09。

考虑空化泡的可压缩性，通过修正RNG-湍流模型[28-29]，降低空化区域湍流黏度。修正公式为

式中为常数，当取不同的值时，密度变化函数如图1所示。本文中，取值为10。

1.3 空化模型

基于-方程的均相流空化模型常用于空化流动的数值计算。含沙水流条件下，方程（3）中的源项+和-采用-空化模型[30-31]。此空化模型中不存在经验系数，系完全推导而来，是一种较为理想的空化模型。

式中b为空化泡半径，m；v为饱和蒸汽压，Pa。

2 流场数值求解

2.1 几何模型与网格划分

以设计参数为流量d=250 m3/h, 扬程d=50 m，转速=1 480 r/min的单级单吸离心泵为研究对象。其几何参数为：叶片数=6，叶轮外径2=420 mm，包角=120°，蜗壳基圆直径3=445 mm。采用Pro/E进行三维建模，整个离心泵模型由叶轮、蜗壳、进水管路、出水管路四部分组成；通过ANSYS-ICEM软件，采用适应性较强的四面体非结构化网格离散计算域，如图2所示。为了对网格无关性进行验证，采用5种不同数目的网格，通过Fluent15.0计算清水介质额定工况下离心泵的流场，计算结果如表1所示。

表1 网格无关性验证

由表1可知，随网格数增加，所得扬程相对误差控制在0.13%以内，说明所采用的网格达到收敛要求，故在后续含沙水空化流动计算中采用中等数量网格的方案3。

2.2 物性参数与边界条件

液相密度l=998.2 kg/m3，黏度l=0.001 kg/m·s，沙粒相密度s=2 650 kg/m3，黏度s=1.72×10-5kg/m·s；汽相密度v0.025 58 kg/m3，黏度v=1.26×10-6kg/m·s；汽化压力v=3 540 Pa；空化泡半径b=1.0×10-5m，空化泡数密度b=1.0×1013。温度为300 K。

边界条件设置为速度进口与压力出口，与常规的压力进口与速度出口设置相比，两者数值计算结果与试验结果差别均较小，以喷嘴空化条件下的流量系数d[32]为例进行说明。2种不同边界条件下的数值计算结果分别为0.632与0.635，文献[32]所提供试验值为0.620，三者相比，差别较小。近壁面采用标准壁面函数处理。通过SIMPLEC算法求解压力速度耦合方程组，压力项、动量项、湍动能与湍流耗散率项均采用二阶迎风格式，残差设定为1.0×10-4。

式中d为流量系数；为质量流量，kg/s；为横截面积，m2；1、2分别为喷嘴进、出口压力，Pa。

3 算法验证

3.1 离心泵外特性验证

图3为离心泵性能试验台。试验台由模型泵、进水管路、出水管路、压力表、流量计、阀门等组成。模型泵由上海凯泉泵业集团有限公司提供，型号为KQL250/400-110/4。压力表由上海自动化仪表制造厂制造，型号为XU12087105型压力表，精确度等级为2.5。流量计由天津仪表流量有限公司制造，型号为DN300型流量计，精度等级为1.0级。阀门由天津百利二通机械有限公司制造，型号为ZA2.T型阀门。基于上述三维离心泵模型，计算不同工况下清水介质的扬程与效率，如图4所示。对比表明，计算结果与试验结果吻合良好，扬程相对误差最大值为6.00%，效率相对误差最大值为5.14%，验证了算法的可靠性。同时，扬程与效率的数值计算结果均高于试验结果，原因为数值模拟过程中，采用的是未考虑口环间隙泄漏损失的非全流场。

a. 流量-扬程性能曲线

a．Head-flow rate characteristic curve

3.2 空化流动验证

通过计算平头圆柱空化流动且绘制相应的压力分布曲线，并与试验结果相对比[33]，以此验证模型及算法的合理性。圆柱直径=5 mm，长度=5，计算域高度和宽度均为10，计算域及网格如图5a所示。计算域采用速度进口与压力出口，压力由空化数确定。圆柱表面为无滑移边界，上下边界为滑移边界。基于圆柱直径的雷诺数为1.36×105，空化数为0.5。如图5b所示为圆柱表面时均压力系数分布图，相对误差为1.1%，计算结果与试验结果吻合良好，进一步验证了空化流动算法的可靠性。

a. 平头圆柱计算域及网格

a. Computational domain and grids of flat-nosed cylinder

b. 平头圆柱表面时均压力系数分布

b. Distribution of time-averaged pressure coefficient of flat-nosed cylinder

注：图5b中，雷诺数为1.36×105，空化数为0.5；为圆柱表面距圆柱头部距离；为圆柱直径。

Note: In Fig.5b, Reynolds number is 1.36×105and cavitation number is 0.5；is distance between surface with head of flat-nosed cylinder;is diameter of flat-nosed cylinder

图5 平头圆柱空化流动模型及结果

Fig.5 Model and results of cavitation flow of flat-nosed cylinder

4 计算结果及分析

4.1 沙粒粒径对离心泵空化特性的影响

通过调研得到黄河兰州段流经工农坪泵站的中值粒径为0.010 mm，因而以0.010 mm为基准，分别再选择2个粒径，为0.005与0.015 mm。以粒径分别为0.005、0.010、0.015 mm，含沙量为1.0%的沙粒为研究对象，计算了不同粒径下的含沙水空化流动。通过与清水介质下的相比较，研究粒径对离心泵空化特性的影响，图6为清水介质，含沙量为1.0%、不同粒径下的含沙水空化性能曲线。

出口压力为6.0×105Pa时，清水介质中无空化泡产生，如图7a所示；而不同粒径的含沙水流中，叶片背面靠近进口边处均有少量空化泡产生，如图7b、7c、7d所示的叶轮进口深色区域。同时由图7b、7c、7d可得，沙粒所携带的空化核子对空化泡形成具有显著影响，但由于出口压力过高，粒径的不同对空化泡产生的影响并不明显。

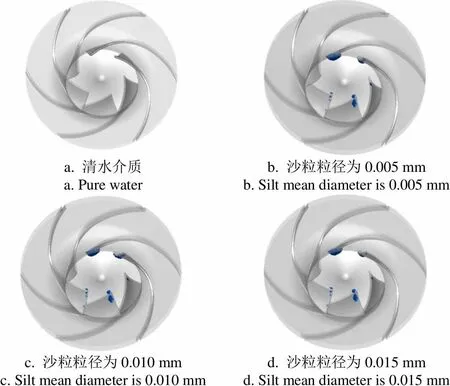
a.清水介质a. Pure waterb. 沙粒粒径为0.005 mmb. Silt mean diameter is 0.005 mm c. 沙粒粒径为0.010 mmc. Silt mean diameter is 0.010 mmd. 沙粒粒径为0.015 mmd. Silt mean diameter is 0.015 mm

离心泵扬程下降3.0%时所对应的空化余量为一临界空化余量，以NPSHc表示。清水介质下，NPSHc为3.721 4 m；粒径为0.005 mm时，NPSHc为4.952 m，表明沙粒促进了空化的提前发生。粒径为0.010 mm时，NPSHc为3.747 9 m，与清水介质下的值近似相等，相对差值为0.63%，表明粒径为0.010 mm的沙粒对空化初生的影响并不明显。粒径为0.015 mm时，NPSHc为3.638 m，小于清水条件，表明沙粒抑制了空化的提前发生。

进一步降低出口压力至5.29×105Pa时, 空化充分发展。清水介质以及粒径为0.005、0.010、0.015 mm的含沙水流所对应的空化余量分别为3.436、3.541、3.438 、3.337 m，表明随粒径的增加，沙粒对空化的影响表现为先促进、后抑制，这与临界空化时的结果相一致，空化泡分布如图8所示。清水介质下扬程为50.26 m，含沙水流下随粒径增加，扬程分别为49.97、49.94、48.69 m，由于沙粒的磨蚀与空蚀的共同作用，使得含沙条件下扬程均低于清水介质下的扬程，且随粒径增大扬程逐渐降低。

综上分析可知，粒径为0.005 mm，含沙量为1.0%的沙粒促进空化的发展，主要原因为：沙粒诱导产生更多的空化核子，从而形成更多的空化泡[34]；沙粒作为一种不被润湿的固体颗粒，具有比清水介质破裂更大的拉应力[35]；同时沙粒在虚拟质量力[36]的作用下，使得混合相具有较高的动能，从而局部压力降低，有效促进空化的发展。清水介质中，最低压力为−1.323×105Pa，粒径为0.005 mm，含沙量为1.0%的含沙水流中，最低压力为−1.33×105Pa，说明沙粒在虚拟质量力作用下，局部压力得到降低。粒径为0.005 mm，含沙量为1.0%的沙粒对流场结构破坏较清水介质下严重，如图9a、9b所示，从而加剧能量损失，致使压力降低，促进空化发展。

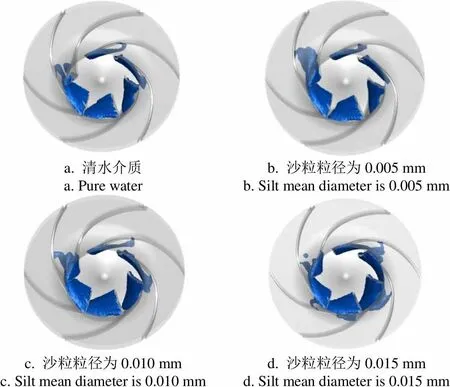
a.清水介质a. Pure waterb. 沙粒粒径为0.005 mmb. Silt mean diameter is 0.005 mm c. 沙粒粒径为0.010 mmc. Silt mean diameter is 0.010 mmd. 沙粒粒径为0.015 mmd. Silt mean diameter is 0.015 mm

粒径为0.015 mm，含沙量为1.0%的沙粒抑制空化的发展，主要原因为：一方面随粒径的增加，粘滞性的抑制作用强于沙粒的促进作用，另一方面，粒径为0.015 mm，含沙量为1.0%的沙粒对流场结构的破坏较粒径为0.005 mm，含沙量为1.0%的沙粒与清水介质下的小，如图9c所示，从而使得压力变大，高于清水介质，一定程度上抑制了空化的发展。

4.2 含沙量对离心泵空化特性的影响

以粒径为0.010 mm，含沙量分别为0.5%、1.0%、1.5%的沙粒为研究对象，计算不同含沙量下的空化流动并与清水介质进行比较，研究含沙量变化对离心泵空化特性的影响。图10为清水介质，粒径为0.010 mm、不同含沙量下的含沙水空化流动性能曲线。

出口压力为6.0×105Pa时，清水介质中无空化泡形成，如图11a所示；含沙量分别为0.5%、1.0%、1.5%时，叶片背面进口边处均出现少量空化泡，如图11b、11c、 11d所示，表明沙粒的存在促进了空化泡的产生，同时，含沙量的不同对空化泡的分布影响较小。

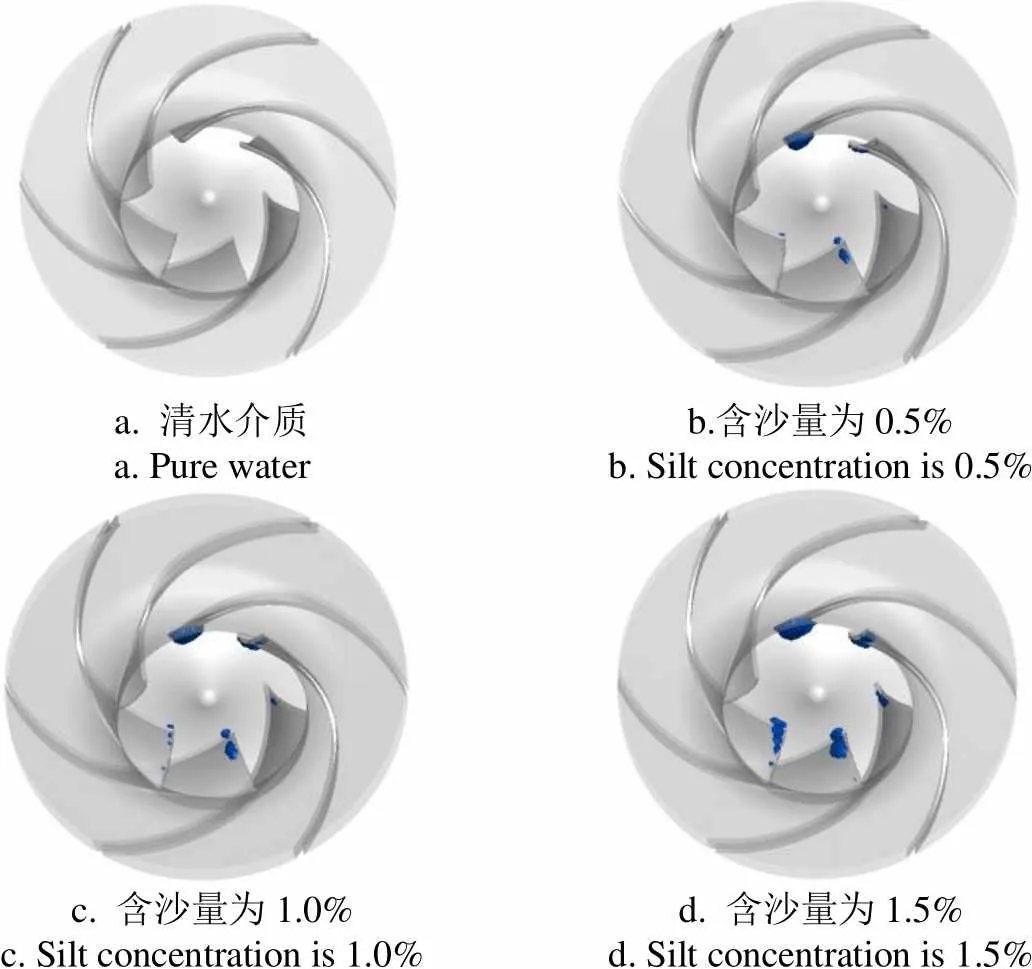
a.清水介质a. Pure waterb.含沙量为0.5%b. Silt concentration is 0.5% c. 含沙量为1.0%c. Silt concentration is 1.0%d. 含沙量为1.5%d. Silt concentration is 1.5%

清水介质中NPSHc为3.721 4 m，含沙量为0.5%时，NPSHc为4.780 1 m，表明沙粒促进空化的提前发生。含沙量为1.0%时，NPSHc为3.747 9 m，与清水介质相比，两者相对误差为0.55%，表明沙粒对空化初生的影响较小。含沙量为1.5%时，NPSHc为3.490 6 m，表明沙粒抑制空化的发展。

空化在出口压力为5.29×105Pa时得到充分发展，清水介质、含沙量分别为0.5%、1.0%、1.5%的含沙水流所对应空化余量分别为3.436、3.841、3.438、2.960 4 m，表明：随含沙量的增加，沙粒对空化发展的影响表现为先促进，后抑制。空化泡分布如图12所示，含沙水流中，空化泡分布与清水介质下的相比较，表现为先变大、再接近、后变小。清水介质下扬程为50.26 m，含沙水流下随含沙量增加，扬程分别为50.04、49.94、40.61 m，表明，由于沙粒的磨蚀作用、沙粒摩擦对能量的消耗、沙粒对流场结构破坏[37]以及空蚀的破坏，使得含沙条件下空化充分发展时的扬程均低于清水介质，且随含沙量的增加，扬程逐渐变小。

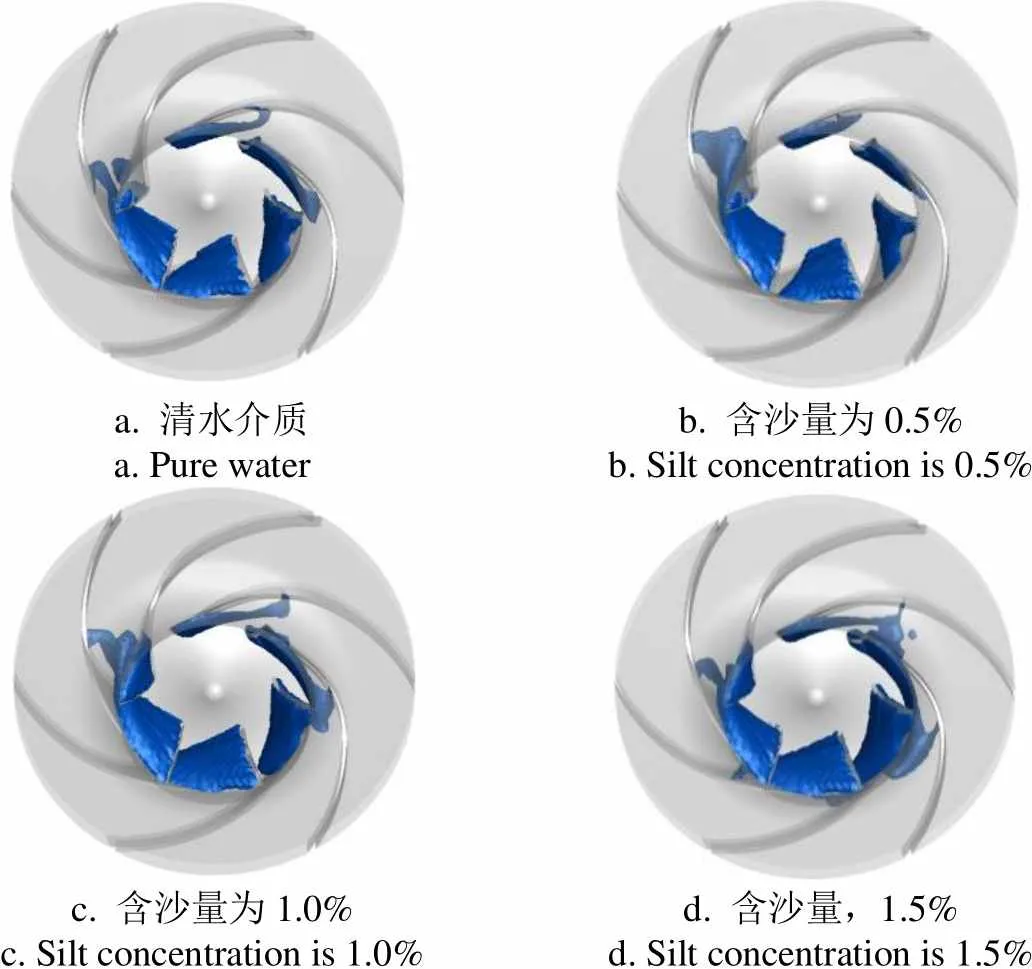
a.清水介质a. Pure waterb. 含沙量为0.5%b. Silt concentration is 0.5% c. 含沙量为1.0%c. Silt concentration is 1.0%d. 含沙量，1.5%d. Silt concentration is 1.5%

综上分析可得，粒径为0.010 mm，含沙量为0.5%的沙粒促进空化发展，主要原因为，沙粒对空化核子、拉应力与虚拟质量力的影响与粒径为0.005 mm的沙粒的促进作用相类似。同时沙粒与清水密度差的影响，当水流减速运动时，由于沙粒惯性的影响，沙粒速度高于清水介质速度，两者间的速度差，使得沙粒某处压力降低，使得该点处流场压力降低，进而促进空化的发展[38-39]。清水介质中，最低压力为−1.323×105Pa，粒径为0.010 mm，含沙量为0.5%的含沙水流中，最低压力为−1.342×105Pa，表明压力在上述因素作用下，得到有效降低。另一方面，粒径为0.010 mm，含沙量为0.5%的沙粒对流场结构破坏较清水介质下严重，如图13a、13b所示，从而加剧能量损失，致使压力降低，促进空化发展。

粒径为0.010 mm，含沙量为1.5%的沙粒抑制空化发展，主要原因为，含沙量为1.5%时，沙粒粘滞性起主导作用，即此时抑制作用强于空化核子、拉应力与虚拟质量力等的促进作用，因而此时沙粒抑制空化发展。粒径为0.010 mm，含沙量为1.5%的沙粒对流场结构的破坏较清水介质下的小，如图13a、13c所示，使得压力变大，高于清水介质，一定程度上抑制空化发展。

5 结 论

为了研究沙粒对离心泵空化特性的影响，本文通过计算不同粒径、含沙量下的含沙水空化流动，得到如下结论：

1）出口压力为6.0×105Pa，清水介质中未出现空化泡；含沙条件下，均有少量空化泡出现；表明沙粒的存在对空泡的形成具有明显的影响。

2）出口压力为含6.0×105Pa，沙量为1.0%时，清水介质中临界空化余量值为3.721 4 m，沙粒粒径分别为0.005、0.010、0.015 mm时，临界空化余量分别为4.952、3.747 9、3.638 m，表明沙粒粒径对空化的影响呈现为先促进、后抑制的变化趋势。

3）出口压力为含6.0×105Pa，粒径为0.010 mm时，清水介质中临界空化余量值为3.721 4 m，含沙量分别为0.5%、1.0%、1.5%时，临界空化余量值分别为4.780 1、3.747 9、3.490 6 m，表明含沙量对空化的影响呈现为先促进、后抑制的变化趋势。

4）出口压力为5.29×105Pa，空化充分发展时，同一含沙量、不同沙粒粒径与同一粒径、不同含沙量下，空化泡分布均呈现为先增大、再接近、后减小的变化趋势，表明此2种情况下，沙粒对空化的影响均为先促进、后抑制。

[1] 潘森森，彭晓星. 空化机理[M]. 北京：国防工业出版社，2013：5－7.

Pan Sensen, Peng Xiaoxing. Physical Mechanism of Cavitation[M]. Beijing: National Defense Industry Press, 2013: 5－7. (in Chinese with English abstract)

[2] 王勇，刘厚林，袁寿其，等.离心泵非设计工况空化振动噪声的试验测试[J]. 农业工程学报，2012,28(2)：35－38.

Wang Yong, Liu Houlin, Yuan Shouqi, et al. Experimental test on cavitation vibration and noise of centrifugal pump under off-design conditions[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(2): 35－38. (in Chinese with English abstract)

[3] 王松林，谭磊，王玉川. 离心泵瞬态空化流动及压力脉动特性[J]. 振动与冲击，2013，32(22)：168－173.

Wang Songlin, Tan Lei, Wang Yuchuan. Characteristics of transient cavitation flow and pressure fluctuation for a centrifugal pump[J]. Journal of Vibration and Shock, 2013, 32(22): 168－173. (in Chinese with English abstract)

[4] Wei Yingsan, Shen Yang, Jin Shuanbao. Scattering effect of submarine hull on propeller non-cavitation noise[J]. Journal of Sound and Vibration, 2016(370): 319－335.

[5] 司乔瑞，袁寿其，李晓俊，等. 空化条件下离心泵泵腔内不稳定流动数值分析[J]. 农业机械学报，2014，45(5)：84－90.

Si Qiaorui, Yuan Shouqi, Li Xiaojun, et al. Numerical simulation of unsteady cavitation flow in the casing of a centrifugal pump[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(5): 84－90. (in Chinese with English abstract)

[6] 卢加兴，袁寿其，任旭东，等. 离心泵小流量工况不稳定性空化特性研究[J]. 农业机械学报，2015，46(8)：54－58.

Lu Jiaxing, Yuan Shouqi, Ren Xudong, et al. Investigation of instabilities of cavitation at low flow rate of centrifugal pump[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(8): 54－58. (in Chinese with English abstract)

[7] Liu Houlin, Liu Dongxi, Wang Yong, Experimental investigation and numerical analysis of unsteady sheet cavitating flow in a centrifugal pump[J]. Journal of Hydrodynamics, 2013, 25(3): 370－378.

[8] 黎慧青. 离心泵汽蚀磨损失效分析对策措施研究[D]. 广州：华南理工大学，2011.

Li Huiqing. Studies of Cavitation and Fretting Wear of Centrifugal Pump and Counter Measures[D]. Guangzhou: South China University of Technology, 2011. (in Chinese with English abstract)

[9] 李根生，沈晓明，施立德，等. 空化和空蚀机理及其影响因素[J]. 石油大学学报，1997，21(1)：97－102.

Li Gensheng, Shen Xiaoming, Shi Lide, et al. Review of studies on cavitation and cavitation erosion[J]. Journal of the University of Petroleum, 1997, 21(1): 97－102. (in Chinese with English abstract)

[10] Zhang Yuning, Qian Zhongdong, Ji Bin. A review of microscopic interactions between cavitation bubbles and particles in silt-laden flow[J]. Renewable and Sustainable Energy Reviews, 2016, 56: 303－318.

[11] 吴玉林，唐学林，刘树红，等. 水力机械空化和固液两相流体动力学[M]. 北京：中国水利水电出版社，2007.

[12] 常近时. 水质状况对泵装置空化性能的重要影响[J]. 排灌机械，2008，26(2)：23－27.

Chang Jinshi. Important effect of state of water quality on cavitation pressure performance of pump device[J]. Drainage and Irrigation Machinery, 2008, 26(2): 23－27. (in Chinese with English abstract)

[13] 王磊，常近时. 考虑水质状况的空化流计算理论[J]. 农业机械学报，2010，41(3)：62－66.

Wang Lei, Chang Jinshi. Computational theory of cavitating flows with consideration of influence of water quality[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010, 41(3): 62－66. (in Chinese with English abstract)

[14] 常近时. 工质为浑水时水泵与水轮机的空化与空蚀[J]. 排灌机械工程学报，2010，28(2)：93－97.

Chang Jinshi. Cavitation and cavitation erosion of pump and turbine with silt-laden water as working medium[J]. Journal of Drainage and Irrigation Machinery Engineering. 2010, 28(2): 93－97. (in Chinese with English abstract)

[15] 王磊，朱茹莎，常近时. 青铜峡与八盘峡水电站水中泥沙含量对空化压力的影响[J]. 水力发电学报，2008，27(4)：45－47.

Wang Lei, Zhu Rusha, Chang Jinshi. Effect of sand concentration in water on cavitation pressure in Qingtongxia and Bapanxia hydropower stations[J]. Journal of Hydroelectric and Engineering, 2008, 27(4): 45－47. (in Chinese with English abstract)

[16] Huang Si, Ihara A, Watanabe H. Effects of solid particle properties on cavitation erosion in solid-water mixtures[J]. Journal of Fluids Engineering, 1996, 118: 749－755.

[17] Dunstan P J, Li S C. Cavitation enhancement of silt erosion: Numerical studies[J]. Wear, 2010, 268: 946－954.

[18] 铁占续，黄建德. 含沙水汽蚀对离心泵损伤的试验研究[J].化工设备与管道，2000，37(3)：42－44.

Tie Zhanxu, Huang Jiande. Damage test and research of sand and water cavitation for centrifugal pumps[J]. Process Equipments & Piping, 2000, 37(3): 42－44. (in Chinese with English abstract)

[19] 黄建德，张奎亭，陈涟. 含砂水对离心泵叶轮磨损的实验研究[J]. 工程热物理学报，1999，20(4)：448－452.

Huang Jiande, Zhang Kuiting, Chen Lian. Experimental studies on the damage of centrifugal impeller due to the sand mixed in water[J]. Journal of Engineering Thermophysics, 1999, 20(4): 448－452. (in Chinese with English abstract)

[20] Chen Haosheng, Liu Shihan, Wang Jiadao. Study on effect of microparticle’s size on cavitation erosion in solid-liquid system[J]. Journal of Applied Physics, 2007, 101(10): 1－5.

[21] Poulain S, Guenoun G, Gart S. Particle motion induced by bubble cavitation[J]. Physical Review Letters, 2015, 114(21): 1－5.

[22] Mizushimaa Y, Nagamia Y, Nakamuraa Y. Interaction between acoustic cavitation bubbles and dispersed particles in a kHz-order-ultrasound-irradiated water[J]. Chemical Engineering Science, 2013, 93: 395－400.

[23] Madadnia J, Owen I. Accelerated surface erosion by cavitating particulate-laden flows[J]. Wear, 1993, 165(1): 113－116.

[24] Madadnia J, Owen I. Erosion in conical diffusers in particulate-laden cavitating flows[J]. International Journal of Multiphase Flow, 1995, 21(6): 1253－1257.

[25] Gregorc B, Hribersek M, Predin A. The analysis of the impact of particles on cavitation flow development[J]. Journal of Fluids Engineering, 2011, 133(11): 4－11.

[26] Zhao Weiguo, Han Xiangdong, Liu Ming, et al. Numerical simulation of effects of sand grains and volume fractions on mass transferring from the water-liquid to the water-vapor[C]// The 7thInternational Conference on Pumps

and Fans. Hangzhou, China, 2015.

[27] 朱红钧，林元华，谢龙汉. Fluent 12 流体分析及工程仿真[M]. 北京：清华大学出版社，2011：88－91.

[28] Coutier-Delgosha O, Reboud J L, Delannoy Y. Numerical simulation of the unsteady behaviour of cavitating flow[J]. Int. J. Numer Meth Fluids, 2003, 42: 527－548.

[29] Coutier-Delgosha O, Stutz B, Vabre A, et al. Analysis of cavitating flow structure by experimental and numerical investigations[J]. J. Fluid Mech., 2007, 578: 171－222.

[30] Schnerr G H, Sauer J. Physical and numerical modeling of unsteady cavitation dynamics[C]//Proceedings of the 4th International Conference on Multiphase Flow, New Orleans, La, USA, 2001.

[31] Schnerr G H, Sezal I H, Schmidt S J. Numerical investigation of three-dimensional cloud cavitation with special emphasis on collapse induced shock dynamics[J]. Physics of Fluids, 2008, 20(4): 3－11.

[32] Nurick W H. Orifice cavitation and its effect on spray mixing[J]. Journal of Fluids Engineering, 1976, 98(4): 681－687.

[33] Rouse H, McNown J S. Cavitation and Pressure Distribution, Head Forms at Zero Angle of Yaw[M]. Iowa: State University of Iowa, 1948: 12－39.

[34] 朱茹莎. 含沙河流水电站水轮机吸出高度的合理确定[D]. 北京：中国农业大学，2008.

Zhu Rusha. Rational Determination of Draft Head of the Turbine in the Silt-Laden Hydropower Station[D]. Beijing: China Agricultural University, 2008. (in Chinese with English abstract)

[35] 黄继汤. 空化与空蚀的原理及应用[M]. 北京：清华大学出版社，1991：7－8.

[36] 袁亚雄，张小兵. 高温高压多相流体动力学基础[M]. 哈尔滨：哈尔滨工业大学出版社，2004：71－74.

[37] 黄思杰，邵春雷. 输送多组分介质的离心泵内部固液两相流特性[J]. 农业工程学报，2016，32(20)：77－84.

Huang Sijie, Shao Chunlei. Solid-liquid two-phase flow characteristics in centrifugal pump with multi-component medium[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(20): 77－84. (in Chinese with English abstract)

[38] 王智勇. 基于FLUENT软件的水力空化数值模拟[D]. 大连：大连理工大学，2006.

Wang Zhiyong. Numerical Simulation of Hydrodynamic Cavitation Based on FLUENT[D]. Dalian: Dalian University of Technology, 2006. (in Chinese with English abstract)

[39] 程则久，段生孝，党云平，等. 含沙河流水轮机安装高程的选定试验研究[J]. 水力发电，1996(10)：34－37.

Chen Zejiu, Duan Shengxiao, Dang Yunping, et al. Test and study on setting height of water turbine in silt-laden water[J]. Journal of Hydroelectric Engineering, 1996(10): 34－37. (in Chinese with English abstract)

Effects of silt diameter and silt concentration on cavitation flow in centrifugal pump

Zhao Weiguo, Han Xiangdong, Li Rennian, Zheng Yingjie, Pan Xuwei

(1.,,730050,; 2.,730050,)

To study the effects of sand particles on the cavitation flow in the centrifugal pump, the method of computational fluid dynamics (CFD) was employed to study the internal cavitation flow field of the centrifugal pump in the pure water and sand water respectively. Based on Fluent 15.0, Mixture model, RNG-(renormalization group) turbulence model and Schnerr-Sauercavitation model were used to research the cavitation flow. For the cavitation flow in the sand water, sand mean diameters selected were 0.005, 0.010 and 0.015 mm and sand concentrations were 0.5%, 1.0% and 1.5% respectively. Unstructured grids constructed by ANSYS-ICEM(Integrated Computer Engineering and Manufacturing), were applied to disperse the computational domain. Accuracy of numerical calculation was improved by grids independence check and the total number used was 2 817 398. Numerical results of pure water performance of the centrifugal pump and cavitation flow around the flat-nosed cylinder were compared with the experimental results to verify the reasonableness of the algorithm used in the simulations. Numerical results revealed that the algorithm designed was appropriate to simulate cavitation flow. To lower the turbulent viscosity in cavitation region, RNG-turbulence model was modified. Cavitation performance curves were built, the vapor had the volume fraction of 0.1 in different cavitation periods, and the effect of sand particles on the cavitation flow was investigated. To study the effect of sand mean diameter, sand concentration was 1.0% and sand mean diameter was increased from 0.005 to 0.015 mm gradually. When the outlet pressure was 6.0×105Pa, cavitation did not occur in the pure water of the centrifugal pump and vapor did not exist in the pure water. In the sand water, a few cavitation bubbles appeared. For the critical net positive suction head (NPSHc) which was the NPSH when the head was reduced by 3.0%. In the pure water, it was 3.721 4 m and in the sand water with sand mean diameter of 0.005, 0.010 and 0.015 mm, it was 4.952, 3.747 9 and 3.638 m respectively, and when cavitation developed fully, theNPSH was 3.436, 3.541, 3.438 and 3.337 m respectively for the pure water and the sand water with 3 different sand mean diameters, indicating that the effects of sand particles on the cavitation flow were accelerative at first, and then inhibited. When sand mean diameter was 0.010 mm, in the critical cavitation stage and cavitation full development stage, NPSH in the pure water and sand water had inconspicuous difference. Compared with cavitation occurring in the pure water, when sand mean diameter was 0.010 mm, sand particles had little effect on the development of cavitation in the sand water. To study the effect of sand concentration, sand mean diameter was 0.010 mm and sand concentration increased from 0.5% to 1.5% gradually. Under outlet pressure of 6.0×105Pa, cavitation did not occur in the pure water of the centrifugal pump and vapor did not appear in the pure water too. And a few cavitation bubbles existed in the sand water, stating clearly that sand particles had a close relation with the formation of cavitation bubbles. In the critical cavitation period, NPSHc was 3.721 4, 4.780 1, 3.747 9 and 3.490 6 m respectively for the pure water and the sand water with 3 different sand concentrations of 0.5%, 1.0% and 1.5%, and in the cavitation full development period, NPSHwas 3.436, 3.841, 3.438 and 2.960 4 m separately, explaining that effects of sand concentration on the cavitation flow were accelerative at first, and then inhibited too. When sand concentration was 1.0%, in the critical cavitation period and cavitation full development period, NPSH in the pure water and sand water had little difference, illustrating that compared with cavitation occurring in the pure water, sand particles had little effect on the development of cavitation under the 1.0% sand concentration. When sand particles promoted the development of cavitation, volume of vapor with volume fraction of 0.1 in sand water was larger than that in the pure water. During sand particles inhibiting the development of cavitation, the volume was smaller than that in the pure water. For sand particles had little effect on the evolution of cavitation, the distribution was similar. During cavitation fully evolving, interaction of abrasion and cavitation erosion made the head in sand water less than that in the pure water. With sand concentration being invariant, when sand mean diameter increased and with sand mean diameter being constant, when volume fraction increased gradually, head in sand water decreased continuously. Number of cavitation nuclei, virtual mass force, slip velocity, and so on had a close connection with sand particles promoting the development of cavitation. Viscosity, abrasion effect, and so on had a close relationship with sand particles inhibiting the evolution of cavitation.

centrifugal pumps; computer simulation; models; cavitation; silt mean diameter; silt concentration

10.11975/j.issn.1002-6819.2017.04.017

TH311

A

1002-6819(2017)-04-0117-08

2016-06-08

2017-02-07

国家自然科学基金项目资助（51269011）；甘肃省高等学校基本科研业务费。

赵伟国，男，山东东营人，博士，副教授，主要从事流体机械空化与空蚀机理研究。兰州 兰州理工大学能源与动力工程学院，730050。 Email：zhaowg@zju.edu.cn

赵伟国，韩向东，李仁年，郑英杰，潘绪伟. 沙粒粒径与含沙量对离心泵空化特性的影响[J]. 农业工程学报，2017，33(4)：117－124. doi：10.11975/j.issn.1002-6819.2017.04.017 http://www.tcsae.org

Zhao Weiguo, Han Xiangdong, Li Rennian, Zheng Yingjie, Pan Xuwei. Effects of silt diameter and silt concentration on cavitation flow in centrifugal pump[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(4): 117－124. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.04.017 http://www.tcsae.org