二分之五次方抛物线形明渠设计及提高水力特性效果

韩延成，徐征和，高学平，Said M. Easa



二分之五次方抛物线形明渠设计及提高水力特性效果

韩延成1，徐征和1，高学平2，Said M. Easa3

（1. 济南大学资源与环境学院，济南 250022； 2. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；3. Dept. of Civil Engineering, Ryerson Univ., Toronto, ON, Canada, M5B 2K3）

为提高抛物线形断面的水力特性，增加输水能力，该文提出了一种二分之五次（以下简称2.5次）方抛物线形渠道断面，推导其水力断面特性。将湿周用高斯超几何函数表示后，将水力最优断面的最优化模型转换为关于宽深比的一元方程，得到2.5次方抛物线形渠道水力最优断面的解析解，其最优宽深比为2.088 3。比较结果表明，2.5次方抛物线形断面较常规抛物线形断面具有更好的水力学特性。与平方、半立方抛物线形断面比较，在相同水深条件下，2.5次方抛物线形水力最优断面的过流能力更大。相反，在相同流量下，2.5次方抛物线形水力最优断面的过流面积、湿周、水深更小。2.5次方抛物线形水力最优断面的建造成本与其他2种断面相比是最小的。进一步地，为便于工程应用，基于高斯勒让德算法，提出2.5次方抛物线形断面的三点和四点格式近似湿周算法。结果表明，四点格式近似算法具有较高精度。研究可为明渠设计提供理论依据。

渠道；水力学；设计；明渠；二分之五次方抛物线形断面；水力最优断面；湿周

0 引 言

渠道输水断面对渠道过流能力、水深、建造成本等均有很大的影响。常见的渠道输水断面为梯形、矩形断面。随着渠道建造工艺的改进，大型衬砌机器的应用，曲线形断面的建造越来越容易，也越来越受到欢迎。例如巴基斯坦的High Level渠，西班牙Genil-Cabra渠等[1]均采用了平方抛物线形断面。学者们普遍认为曲线形断面有以下优点[2-4]：曲线形渠道断面没有或拐角点少、应力集中点少，因而由应力集中可能产生的裂缝少，渗漏量少；自然形成的河道或非衬砌渠道更多呈现曲线形断面的形状；曲线形渠道断面从渠底到渠堤边坡是渐变的，因而稳定性更好；曲线形渠道具有更好的水力学特性。

常见的抛物线形渠道断面主要包括平方抛物线形断面和半立方抛物线形断面。学者们对常规的抛物线形断面已经进行了大量研究，不仅研究了平方抛物线形渠道的水力最优断面[2,5]、经济断面[6]，也研究了具有抛物线形底和三角形边坡的复合断面[7]，平底的平方抛物线形断面[3-4]，以及平底的半立方抛物线形断面[8]等。为方便工程应用，张新燕等[9]进行了抛物线形断面渠道正常水深的显式计算研究，文辉等[10]进行了平底的马蹄形断面的水力计算，王正中等[11]进行了收缩断面的显式计算研究，文辉等[12]进一步开展了抛物线形渠道恒定渐变流水面线的计算方法的研究。然而，在宽度和深度相同的情况下，平方抛物线形和半立方抛物线形断面的底部较尖，可能仍然会影响过流能力。为提高抛物线形断面的水力学特性，提高输水能力，本文提出了一种二分之五次（以下简称2.5次）方抛物线形断面，并对该抛物线形的水力断面特性、最优断面的解析解、近似湿周算法等进行研究，以便于工程应用。

1 2.5次方抛物线形渠道断面及其特性

1.1 断面形状

2.5次抛物线形断面形状如图1所示。与平方抛物线和半立方抛物线相比较，2.5次抛物线形断面具有更加平坦的底部，这有利于施工、底部压实及增加过流能力。

以抛物线断面底部中心为原点建立-坐标系，2.5次抛物线形断面可表示为

式中为形状系数。

由图1可知，当为水面宽度的1/2（=/2）时，存在=（为水深），可用和表示为

由式（2），可用和表示为

1.2 面积与湿周

2.5次方抛物线渠道过水断面的面积可用积分方法得到，为

2.5次方抛物线渠道的湿周可用弧长法求得，为

式中为湿周，m。

1.3 湿周的显式近似解

式（5）中的湿周为积分形式，需要用数值方法求得。为便于工程应用，求解简单的显式求解算法是必要的。本文经过推导，将式（5）用高斯勒让德三点格式表示为[13]

利用式（2），也可用和表示为

用同样的方法，得到基于高斯勒让德四点格式的湿周表达式为

以为0.3为例，比较三点法和四点法计算2.5次方抛物线形渠道为1.0～3.5 m时湿周的精度。将=0.3和值代入式（3）得到，然后代入式（5），用数值积分法求得湿周理论值P。同样，将和分别代入式（6）和式（8）得到基于三点和四点高斯勒让德的湿周近似值3和4（表1）。表中绝对误差为近似值与理论值差值的绝对值。由表1可知，三点法计算的湿周的最大绝对误差为0.004 01 m，四点法湿周的最大绝对误差0.000 97 m。可以看出，四点高斯勒让德近似算法具有较高的精度，更接近理论值。

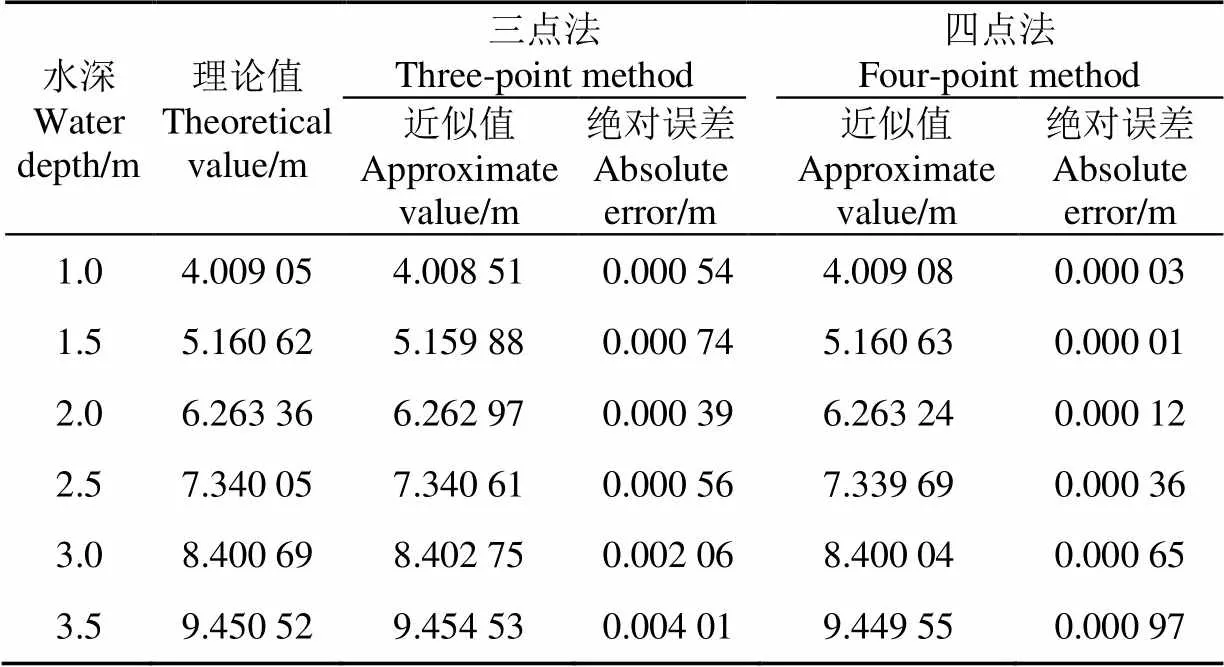
表1 基于高斯勒让德近似算法的湿周值

2 2.5次方抛物线形水力最优断面的解析解

2.1 明渠均匀流

渠道设计流量可按谢才公式表示为[10,13-15]

式中为设计流量，m3/s；为渠底纵坡；为水力半径，m；C为谢才系数。根据曼宁公式[13,16-19]，（为糙率）。因此式（9）可以表示为

2.2 水力最优断面求解模型

水力最优断面是面积一定的情况下，使过流能力最大的断面，或过流能力一定的情况下，使过流面积最小的断面[17, 20-23]。两者得到的最终结果是相同的。因此，求解水力最优断面的模型表示为

目标函数：

约束条件：

式中为等式约束函数。

上式用拉格朗日乘子法可表示为

式中为拉格朗日乘子。

将式（14）代入式（13），消去，并化简后可得到

式（15）即求解2.5次方抛物线形渠道最优水力断面的微分方程。

2.3 水力最优断面的解析解

由式（4）得到对和的偏导数

式（5）中湿周是一个积分形式，难以求导。式（6）或式（8）是近似算法，不适合求解水力最优断面的理论解。此处可以用高斯超几何函数表示为[24-25]

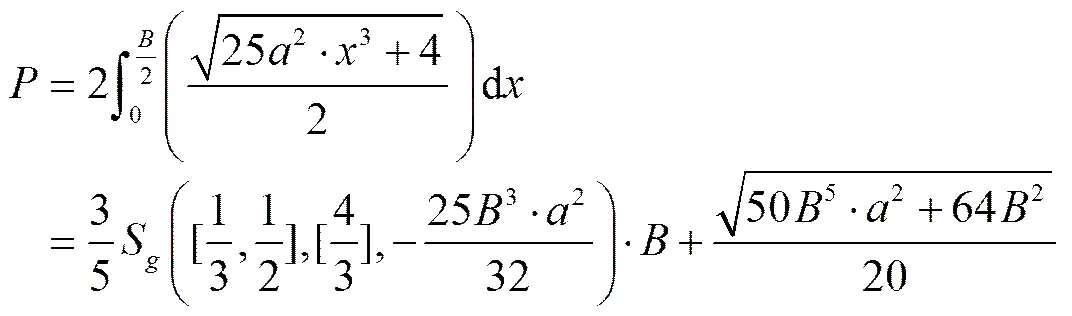
其中S=Hypergeom([1,2],3,4) ，为高斯超几何函数，14为高斯超几何函数的参数。

由式（10），可以求得对和的偏导数分别为

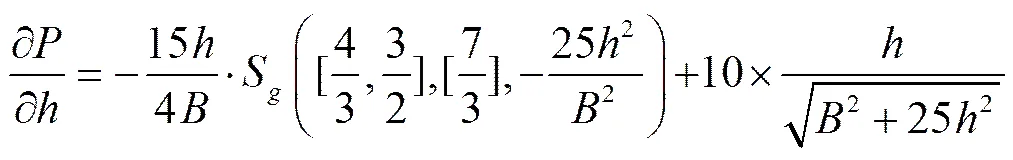
将式（16）、（17）、（20）、（21）代入式（15），简化后得到

（22）

设无量纲参数=/，并将其代入式（22），经过进一步简化可以得到

式（23）只有一个变量，用数值方法求解式（23），可以得到唯一的可行解

因此，2.5次方抛物线形最优断面的宽深比（水面宽与水深比）是一个常数，/=2.088 3。由可以得到其他参数，将代入式（2）可以得到最优断面的形状系数

将/=2.088 3和式（25）代入式（4）可以得到水力最优断面的过流面积的直接计算公式为

=1.491 62（26）

将/=2.088 3和式（25）代入式（18）可以得到水力最优断面的湿周的直接计算公式为

=3.096 33（27）

2.4 水深、水面宽度、过流面积、湿周与流量的关系

将式（26）、（27）代入式（10），可以得到流量的显式计算公式

对上述方程求解，可以得到依据流量直接计算的显式公式

将式（29）代入式（24）～式（27），可以得到

2.5 正常水深和临界水深的计算

正常水深和临界水深是明渠水力学计算的重要参数[26-29]。显然式（29）也是最优断面条件下正常水深的计算公式。

临界水深的通用计算公式为

式中为能量修正系数；为重力加速度，m/s2。

将/=2.088 3和式（26）代入式（35），可以得到临界水深h的显式表达式

2.6 案例分析

2.6.1案例描述

一个2.5次方抛物线形渠道，流量=25 m3/s，=0.014，=1/12 000，=1。要求：1）按2.5次方最优抛物线形断面设计渠道。2）验证最优断面宽深比为2.088 3。

2.6.2结果与分析

1）最优断面设计

将已知条件代入式（29）可得到水深4.055 5 m，代入式（25）得最优形状系数0.109 91。由/=2.088 3得到=8.469 1 m。代入式（36）得临界水深h=2.092 2 m。代入式（26）～（27）或式（32）～（33）得24.533 m2、=12.557 m。

2）最优断面宽深比验证

取=24.533 m2，取0.5～10 m内步长0.000 5 m的不同值，根据式（4）计算得到，将和代入式（2）得到。利用式（5）得到，式（10）得到，绘制/与的关系曲线。如图2所示，面积一定时，=2.09时最大，其结果与式（24）（2.088 3）近似。

3 2.5次方和常规抛物线形最优断面的比较

3.1 过流能力的比较

与平方抛物线形的比较。对于平方抛物线形断面的水力最优断面，、、和分别为

2.055 5，=1.370 32，=2.998，=0.946 7-1（37）

将式（37）代入式（10），可以得到平方抛物线形断面流量的显式计算公式为

求解上式，可以得到平方抛物线形断面正常水深关于的表达式为

比较式（38）和式（28）可知，相同水深情况下，2.5次方抛物线形最优水力断面的流量大于平方抛物线形最优断面的流量；比较式（39）与式（34）也可以得到，相同流量情况下，2.5次方抛物线形最优水力断面的水深小于平方抛物线形最优断面的水深。

将式（39）的代入式（37），可以得到平方抛物线形断面的，和的显式计算公式

用同样的方法，可以得到半立方抛物线形的特性参数如表2。2.5次方抛物线形最优水力断面的过流面积、湿周较半立方抛物线形、平方抛物线形断面的小。

3.2 建设成本比较

渠道的主要建设成本包括土方、衬砌和征地费用。忽略超高的影响后，通用的单位渠长上建造成本可表示为

=W·+W·+W·（43）

式中为单位渠长上建造成本，元；W为单位渠长上，沿横断面上单位面积挖土方成本，元/m2；W为单位渠长上，沿横断面单位长度衬砌成本，元/m；W为单位渠长上，单位渠宽的征地费，元/m。

表2 不同抛物线形渠道水力最优断面的水力特性

注：，为流量，为糙度，为渠底纵坡。

Note:,is discharge,is roughness,is slope of canal base。

对2.5次方抛物线形断面，如果不考虑安全超高的影响，将式（31）～式（33）代入式（43），可以得到2.5次方抛物线形断面单位长度渠道造价为

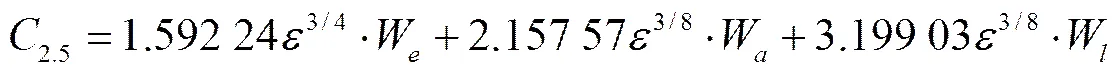
式中2.5为2.5次方抛物线形最优断面单位渠长建造成本，元；。

同样，将式（40）～式（42）代入式（43），可以得到单位渠长平方抛物线形最优断面的建造成本

式中2为平方抛物线形断面单位渠长建造成本，元。

根据表2和式（43），也可以得到半立方抛物线形断面建造成本（单位渠长）

式中1.5为半立方抛物线形断面单位渠长建造成本，元。

比较式（44）～式（46），可以得到

因此，2.5次方抛物线形最优断面的造价是最低的。

实际上，考虑安全超高后，用类似的方法，可得到2.5次方抛物线形最优断面的建造成本小于平方抛物线和半立方抛物线形断面。推导过程不再赘述。

4 结论与讨论

断面设计是输水渠道设计的最重要内容之一，其对渠道输水效率、成本均有显著影响。本文提出了一种二分之五次（以下简称2.5次）方抛物线形明渠输水断面，并对其水力特性、水力最优断面等进行了研究。

2.5次方抛物线形明渠输水断面具有较平坦的渠底，具有良好的水力特性。推导了2.5次方抛物线形渠道水力断面特性。为便于工程应用，提出了基于高斯勒让德算法的三点和四点近似湿周算法，结果表明，四点近似算法具有很高的精度。

建立了2.5次方抛物线形断面的水力最优断面模型，用拉格朗日法推导了最优断面的微分方程。将湿周用高斯超几何函数表示后，将水力最优断面模型转化成了关于宽深比的方程，并最终求得了2.5次方抛物线形断面的水力最优断面。结果表明其最佳宽深比为2.088 3。

利用水力最佳宽深比，进一步得到了水力最优断面条件下的正常水深、临界水深、水面宽、过流面积、湿周的显式计算公式。对比结果表明，水深相同的情况下，2.5次方抛物线形最优水力断面的流量较半立方抛物线形、常规（平方）抛物线形断面的大；相反，在流量相同的情况下，2.5次方抛物线形最优水力断面的过流面积、湿周较半立方抛物线形、平方抛物线形断面的小。建造成本对比结果表明，相同情况下，2.5次方抛物线形最优水力断面的建造成本较半立方抛物线形、平方抛物线形断面的小。

到目前为止，包括梯形、矩形、抛物线形、半圆形、蛋形等在内的多种断面已被应用于渠道或排水管道。这使设计者可以根据地质条件、输水规模、渗漏、经济条件等选择最合适的断面形式。本文提出的2.5次方抛物线形断面为工程提供了一种新的选择。但在实际工程中，仍然需要根据过流能力、水深、地质条件、经济性等选择平方抛物线形断面还是2.5次方抛物线形断面或其他抛物线形断面。不同次方的抛物线形断面均有不同的水力学特点和适宜条件。

本文选择2.5次方抛物线形而不是更高次抛物线形，主要是其相对于平方抛物线形断面，其水力条件有改善，但边坡等方面变化不是很大，因此有较好的实用性，其更多性质及与其他抛物线形断面的比较需要进一步研究。

[1] Anwar A A, de Vries T T. Hydraulically efficient power-law channels[J]. Journal of Irrigation and Drainage Engineering, 2003, 129(1): 18－26.

[2] Mironenko A P, Willardson L S, Jenab S A J. Parabolic canal design and analysis[J]. Journal of Irrigation and Drainage Engineering, 1984, 110(2): 241－246.

[3] Das J A. Optimal design of channel having horizontal bottom and parabolic sides[J]. Journal of Irrigation and Drainage Engineering, 2007; 133(2): 192－197.

[4] Easa S M. Improved channel cross section with two-segment parabolic sides and horizontal bottom[J]. Journal of Irrigation and Drainage Engineering, 2009, 135(3): 357－365.

[5] Loganathan G V. Optimal design of parabolic canals[J]. Journal of Irrigation and Drainage Engineering, 1991, 117(5): 716－735.

[6] Chahar J, Bhagu R. Optimal design of a special class of curvilinear bottomed channel section[J]. Journal of Hydraulic Engineering, 2007, 133(5): 571－576.

[7] Babaeyan-Koopaei K, Valentine E M, Swailes, D C J. Optimal design of parabolic-bottomed triangle canals[J]. Journal of Irrigation and Drainage Engineering, 2000,126 (6): 408－411.

[8] Han Yancheng. Horizontal bottomed semi-cubic parabolic channel and best hydraulic section[J]. Flow Measurement and Instrumentation, 2015, 45: 56－61.

[9] 张新燕，吕宏兴. 抛物线形断面渠道正常水深的显式计算[J]. 农业工程学报，2012，28(21)：121－125. Zhang Xinyan, Lü Hongxing. Explicit solution for normal depth in parabolic-shape channel[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(21): 121－125. (in Chinese with English abstracts)

[10] 文辉，李风玲. 平底马蹄形断面的水力计算[J]. 农业工程学报，2013，29(10)：130－135.Wen Hui, Li Fengling. Hydraulic calculation of horseshoe cross-section with flat-bottom[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(10): 130－135. (in Chinese with English abstract)

[11] 王正中，王羿，赵延风，等. 抛物线形断面河渠收缩水深的直接计算公式[J]. 武汉大学学报：工学版，2011，44(2)：175－177，191. Wang Zhengzhong, Wang Yi, Zhao Yanfeng, et al. Formula for direct calculation of contracted depth of parabola shaped canal[J]. Engineering Journal of Wuhan University, 2011, 44(2): 175－177, 191. (in Chinese with English abstracts)

[12] 文辉，李风玲. 数值积分法计算抛物线形渠道恒定渐变流水面线[J]，农业工程学报，2014，30(24)：82－86. Wen Hui, Li Fengling. Numerical integration method for calculating water surface profile of gradually varied steady flow in parabola shaped channel[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(24): 82－86. (in Chinese with English abstracts)

[13] Chow V T. Open Channel Hydraulics[M]. New York, N Y, United States: McGraw-Hill, 1959.

[14] Chanson H. The Hydraulics of Open Channel Flow: An Introduction[M]. London, UK: Edward Arnold, 1999.

[15] Easa S M. Versatile general elliptic open channel cross section[J]. KSCE Journal of Civil Engineering, 2016, 20(4): 1572－1581.

[16] Easa S M. New and improved channel cross section with piece-wise linear or smooth sides[J]. Canadian Journal of Civil Engineering, 2011, 38(6): 690－697.

[17] Flynn Lawrence E, Marino Miguel A. Canal design: Optimal

cross sections[J]. Journal of Irrigation and Drainage Engineering, 1987, 113(3): 335－355.

[18] Hussein A S. Simplified design of hydraulically efficient power-law channels with freeboard[J]. Journal of Irrigation and Drainage Engineering, 2008, 134(3): 380－386.

[19] Bhattacharjya R K, Satish M G. Optimal design of a stable trapezoidal cross section using hybrid optimization techniques[J]. Journal of Irrigation and Drainage Engineering, 2007, 133(4): 323－329.

[20] Aksoy B, Altan-Sakarya A. Optimal lined channel design[J]. Canadian Journal of Civil Engineering, 2006, 33(5): 535－545.

[21] Guo C, Hughes W. Optimal channel cross section with freeboard[J]. Journal of Irrigation and Drainage Engineering, 1984,110(3): 304－314.

[22] Han Yancheng, Said M Easa. Superior cubic channel section and analytical solution of best hydraulic properties[J]. Flow Measurement and Instrumentation, 2015, 50:169－177.

[23] Abdulrahman A. Best hydraulic section of a composite channel[J]. Journal of Hydraulic Engineering, 2007, 133(6): 695－697.

[24] Abramowitz M, Stegun I A. Handbook of Mathematical Functions[M]. New York: Dover Publications, 1964.

[25] 裘松良. Gauss超几何函数的导数和广义Legendre关系[J]. 杭州电子科技大学学报，1998，18(2)：1－8. Qiu Songliang. Derivatives and generalized Legend’s relation of the Gaussian hypergeometric function[J]. Journal of the Hanzhou Institute of Electronic Engineering, 1998, 18(2): 1－8. (in Chinese with English abstract)

[26] Vatankhaha Ali R, Said M Easa. Explicit solutions for critica and normal depths in channels with different shapes[J]. Flow Measurement and Instrumentation, 2011, 22: 43－49.

[27] 张宽地，吕宏兴，赵延风. 明流条件下圆形隧洞正常水深与临界水深的直接计算[J], 农业工程学报，2009，25(3)：1－5. Zhang Kuandi, Lü Hongxing, Zhao Yanfeng. Direct calculation for normal depth and critical depth of circular section tunnel under free flow[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(3): 1－5. (in Chinese with English abstract)

[28] 张新燕，吕宏兴，朱德兰. U 形渠道正常水深的直接水力计算公式[J]. 农业工程学报，2013，29(14)：115－119. Zhang Xinyan, Lü Hongxing, Zhu Delan. Direct calculation formula for normal depth of U-shaped channel[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(14): 115－119. (in Chinese with English abstract)

[29] Raikar R V, Reddy M S S, Vishwanadh G K. Normal and critical depth computations for egg-shaped conduit sections[J]. Flow Measurement and Instrumentation, 2010, 21(3): 367－372.

Design of two and a half parabola-shaped canal and its effect in improving hydraulic property

Han Yancheng1, Xu Zhenghe1, Gao Xueping2, Said M. Easa3

(1.250022,; 2.300072,; 3.)

Shapes of canal cross sections affect their discharge capacity, water depth and construction cost. Researches have shown that the curve-shaped canal such as quadratic parabolic and semi-cubic parabolic shape has good hydraulic property. However, the less smooth base of the quadratic parabolic and semi-cubic parabolic shape canal can affect the discharge capacity. To improve the hydraulic property and increase the discharge of the quadratic parabolic sections of canals, a section with two and a half parabola shape was proposed in this paper. Formulas for flow area, shape factor and water surface width for this new section were derived. The theoretical formula for the wetted perimeter was deduced using Gauss super-geometric functions. A model of the optimum hydraulic section that minimized the flow area for a given discharge was developed based on the Manning formula. The partial differential equation for the optimum hydraulic section was deduced using Lagrange’s multiplier method. After substituting the derivatives of wetted perimeter and flow area with respect to water depth and water surface width into this partial differential equation, the optimum model was successfully converted into an equation about the water surface width-depth ratio. Various explicit formulas to compute the characteristic’s parameters such as wetted perimeter, shape factor, flow area, normal water depth and critical water depth for the best hydraulic section were obtained. Using these formulas, the hydraulic design could be achieved easily. The results showed that the best ratio of water surface width-depth ratio for the optimum hydraulic section of the two and a half parabola-shaped canal was a constant (2.0 883). The two and a half parabola-shaped canal had better hydraulic properties than that with quadratic or semi-cubic parabolic sections. Comparisons with quadratic and semi-cubic parabolic sections showed that the flow discharge of the two and a half parabola-shaped section was the largest under the same water depth, which means it is an economical section. Under the same discharge, the water depth of the two and a half parabola-shaped section was smaller than the quadratic parabolic and semi-cubic parabolic sections. The flow area, wetted perimeter and water surface width of the two and a half parabola-shaped section was the least under the same discharge among the three sections. Minimum wetted perimeter and flow area implied that the cost of construction (excavation and lining cost) was minimized. In theory, the comparisons with quadratic and semi-cubic parabolic sections also showed that the construction cost of the proposed best hydraulic section was the lowest under the same discharge. To aid practical use, the 3- point and 4-point method of Gauss-Legendre approximate algorithm were presented for the wetted perimeter calculation. The application example with the water depth of 1.0-3.5 m showed that the approximate algorithm was highly accurate. The 3-point approximate format formula could meet the practical use and design with the maximum absolute error of 0.004 01 m. The results from the 4-point format formula almost equaled to those of the theoretical results with the maximum absolute error of 0.000 97 m. This research provides a theoretical basis for the design of the two and a half parabola-shaped canals with improved hydraulic properties.

canals; hydraulics; design; open canal; two and a half parabola-shaped section; optimum hydraulic section; wetted perimeter

10.11975/j.issn.1002-6819.2017.04.019

TV131.4

A

1002-6819(2017)-04-0131-06

2016-04-27

2016-09-10

国家“十二五”科技支撑计划（2015BAB07B02-6）；山东省重点研发计划（2016GSF117038）；南市科技发展计划（201302052）。

韩延成，男，甘肃武威人，副教授，博士，硕士生导师，主要从事水力学及河流动力学方面的研究。济南 济南大学资源与环境学院，250022。Email：stu_hanyc@ujn.edu.cn

韩延成，徐征和，高学平，Said M. Easa. 二分之五次方抛物线形明渠设计及提高水力特性效果[J]. 农业工程学报，2017，33(4)：131－136. doi：10.11975/j.issn.1002-6819.2017.04.019 http://www.tcsae.org

Han Yancheng, Xu Zhenghe, Gao Xueping, Said M. Easa. Design of two and a half parabola-shaped canal and its effect in improving hydraulic property[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(4): 131－136. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.04.019 http://www.tcsae.org