用PIV和LBM法检验灌水器设计中连续介质假设的适用性

马胜利，魏正英，张育斌，陈雪丽，马 超



用PIV和LBM法检验灌水器设计中连续介质假设的适用性

马胜利，魏正英※，张育斌，陈雪丽，马 超

（西安交通大学机械工程学院机械制造系统国家重点实验室，西安 710049）

灌水器由于其流道特征尺寸微小，因而在其流道内的流动特性分析中，基于连续性介质假设的Navier-Stokes（NS）方程是否适用一直存在争议。该文从微观角度采用格子Boltzmann方法（lattice Boltzmann method，LBM）研究灌水器的流动特性。首先进行LBM的网格无关性分析，其次将LBM的数值计算结果、传统的基于连续性介质假设下的有限体积法的计算流体动力学（computational fluid dynamics，CFD）计算结果以及粒子图像测速（particle image velocimetry，PIV）试验结果进行对比，分析LBM计算结果与基于CFD结果偏离PIV试验值的相对偏差的算术平均值。结果表明，CFD偏离PIV试验结果的相对偏差的算术平均值为0.139%，而LBM偏离PIV试验的相对偏差的算术平均值为0.115%，两者偏离PIV试验结果的相对偏差的算术平均值比较接近。因此，针对流道特征尺寸为1 mm的灌水器，采用基于连续性介质假设下的流体动力学计算方法来研究是适用的。

CFD；Boltzmann方程；流速；PIV；连续介质假设；LBM；灌水器

0 引 言

灌水器是滴灌系统的一个核心部件，具有迷宫式的流道结构，这使得其内部流场特性复杂，因此在灌水器设计中，研究灌水器流道内流体的流动特性至关重要[1-3]。在微观流动中，由于流体的特征尺寸小，流体分子的平均自由程与流体的特征尺寸之间的比值相对较大，因而流体的流动规律和物理特性等与宏观流动存在许多差异。灌水器流道的特征尺度较小，其宽度通常在几百到1 000m左右。工程中一般把大于1 mm的尺度称为宏观尺度，介于1～1 000m的尺度称为微尺度。因而灌水器的流道的特征尺度属于微尺度范畴。目前灌水器流道分析过程中存在的不足之处是：所有学者均采用基于连续介质假设方法进行研究[4-8]。但对于描述宏观流体的纳维-斯托克斯方程（Navier-Stokes equations，NS）是否适用于微尺度下灌水器流场的分析一直存在争议，同时从微尺度角度分析灌水器流场特性的相关文献鲜见。李云开等[9-10]认为，灌水器内部为临界尺度流体流动问题，基于宏观尺度研究方法的计算流体动力学（computational fluid dynamics，CFD）在灌水器内部流动分析中应用的可行性还有待于依靠试验测试进行论证。张俊认为[11]，对灌水器流道相关基础理论的研究非常少，采用细尺度研究方法更助于了解灌水器内的复杂流动。

针对微尺度与宏观尺度下流体的流动问题，许多学者做了相关研究，大多认为2种尺度下流体的流动特性是不同。Mala等[12-13]认为微尺度与宏观尺度下流体的流动机理存很大差异；Eringen[14]认为描述微流道内流体流动的方程应不同于常规尺度下流体的流动方程，同时提出了一种简单的微小流体理论的概念，即微连续理论，并指出采用经典的NS方程来描述微流道内的流动存在很大的偏差；Ariman等[15]对微连续流体力学的发展进行了综述，表明微流体的流动已经偏离了宏观流体力学的理论，一些宏观尺度下可忽略的因素在微流体中反而起主导作用；Tuckermann等[16]通过微流动试验发现，微流动过程中出现了许多不同于宏观尺度的物理现象；Harley等[17-19]研究了特征尺度在40m左右的微流道，发现微流道内的摩擦因子一般要小于常规尺度的流道内摩擦因子；Rahman等[20]试验研究发现，流道的高宽比也影响着微流道内的摩擦因子，而这种现象在宏观尺度的流道中不存在；Peng等[21-23]通过试验研究了微流道中临界雷诺数问题，研究发现微流道中层流向湍流转捩的临界雷诺数为200～700，同时临界雷诺数随着微流道的特征尺寸的减小而降低。在近十几年对微流体的研究方法中，格子Boltzmann方法（lattice Boltzmann method，LBM）已成为一种描述流体流动的有前景的数值计算方法。该方法由McNamara等[24]于1988年首次提出，LBM方法可看作是对早期的格子气动机的推广，同时又可看作是对连续Boltzmann方程的一种离散。常规的CFD方法是对NS方程的离散，而LBM方法以统计物理为基础，并采用非常简单的碰撞行为来描述粒子的微观运动，但在宏观层面上却能正确表征流体的流动规律。LBM计算方法简单、容易并行处理，具有能够处理具有复杂边界形状的流道的优势，已成功用于许多领域中数值问题求解[25-31]。本文主要是基于LBM方法，从微尺度角度研究灌水器的流场特性，同时进行粒子图像测速（particle image velocimetry，PIV）试验，验证基于连续介质假设的传统CFD方法模拟灌水器流场特性的可行性。

1 材料与方法

1.1 灌水器

本研究的对象为本课题组设计开发的分流式灌水器[32]。此灌水器的特点是迷宫流道利用了流道的转折，因此将渐缩、渐扩以及分流用到新型灌水器流道设计中，增大流道的消能能力；在抗堵性能方面，流道分流形成双通道，降低了流道完全堵塞的概率，流道的拐角处设计成圆弧过渡形式，减小了固体颗粒在壁面附近的运移阻力。此结构的灌水器其50 kPa下流量为1.6 L/h，其流态指数为0.492。考虑到灌水器中流场的分布是影响灌水器水力性能的关键因素，同时考虑结合PIV试验验证分析，本文对灌水器内流场以及灌水器单元内流速变化剧烈的位置进行了定量分析和对比。

1.2 灌水器流速模拟方法

1.2.1 LBM方法

LBM方法是以分子动理论为基础，因而具有明确的物理背景。此方法在宏观上是离散的，在微观上是连续的，因而属于一种介观的数值计算方法。通常在介观和微观层面下，假设流体依然为连续介质已经不再成立。在LBM方法中，流体被离散为一系列的流体粒子（微团），从粒子尺寸角度而言，这些粒子的尺寸要远大于分子级别，但在宏观层面上又属于无限小；从粒子的质量角度而言，这些流体粒子的质量比起常规的计算流体力学方法中的有限体积法中的控制体的质量要小很多。从统计层面上，单个流体粒子的运动细节并不会影响流体的宏观特性，因而通过构造一定的流体粒子的物理规律的演化机制，让这些流体粒子进行一定的演化计算，从而获得与宏观物理现象完全一致的数值结果。图1绘制了各种流体动力学计算方法的适用范围[33]。从图1可看出，基于连续性假设适用于宏观尺度范围，而LBM方法可延伸至微观尺度流场的计算分析。

LBM可以被离散为单松弛因子下的BGK（Bhatnagar-Gross-Krook）假设，其公式如下：

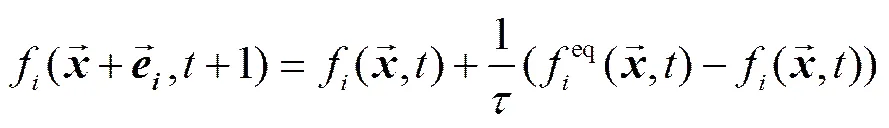
式中是i方向的速度矢量；为格点空间位置矢量；代表着平衡态分布函数；为松弛时间；t为迁移时间。

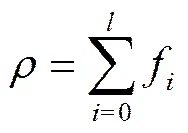
（3）

平衡态分布函数为

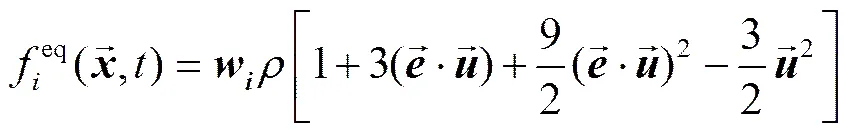
式中w代表方向的权重。LBM的BGK模型针对不可压缩流，即应用在低马赫数时，引入了状态方程和运动学黏附系数，其中为压力；c为与网格相关的声速，在三维的LBM模型D3Q27中，其大小为。

在针对三维流场问题的三维LBM模型如D3Q15, D3Q19和D3Q27中，D3Q27模型具有高度对称性，如图2所示，也因此具有更高的数值稳定性和更高的精度。针对平衡态分布函数，D3Q27的速度矢量以及相对应的权重如下

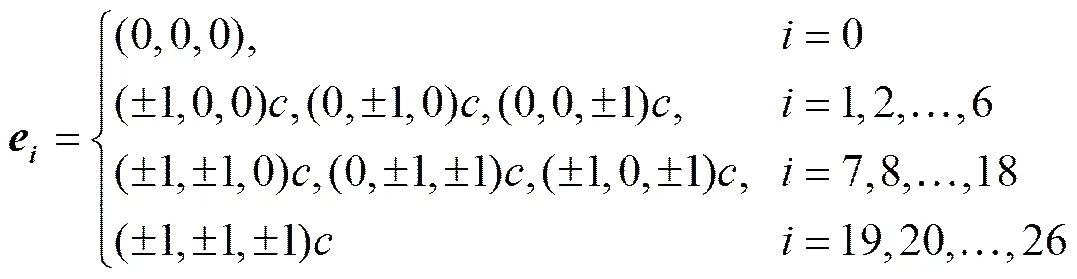
（6）

1.2.2 LBM方法设定

在采用LBM计算之前，需要在三维模型软件中导出模型的STL格式，并在LBM程序中对整个STL模型进行体素化，将STL网格转换为六面体网格。从CVMLCPP库，可以得到任意精度的三维六面体网格。通过布尔运算进行标识，标识位为1的代表区域为流体域，标识位为0则代表为非流体区域。因此，可通过简单的布尔运算迅速扑捉到边界。LBM计算区域的尺寸如表1所示。

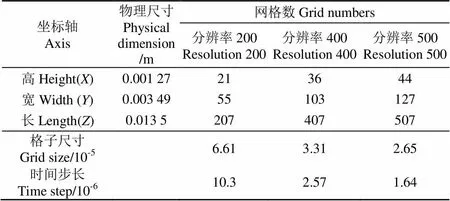
表1 物理尺寸和不同分辨率下的格子尺寸以及对应的时间歩长

LBM采用笛卡尔网格，通过调整体素化参数获得网格的分辨率。采用Fortran语言编译程序，用D3Q27模型计算三维流动。入口边界设置为速度入口，流速为1.5 m/s；出口边界设置为压力边界条件，大小为1 013 kPa。壁面边界条件采用反弹边界条件，即设置为无滑移。流体设置为牛顿流体，属性与CFD以及PIV试验中相同：运动黏度为1.7×10-6m2/s，流体密度为1 140 kg/m3。LBM中数与运动学黏度之间的关系为。其中，δ为特征长度方向上的单位格子尺寸；δ为运动单位格子尺寸所需的时间；为LBM中的运动学黏度系数。分辨率为400时的网格尺寸为3.31×10-5，为了获得与CFD相同的数并考虑到收敛速度，松弛时间设置为0.512（此时松弛频率为2.0）。因此，LBM中的运动学黏度需设置为0.004且时间步长对应为2.6×10-6。格子速度则相应为12.9。格子声速则为7.4。为了获得与CFD相同的入口速度边界条件，最大格子速度的幅值通过（其中u为无量纲系统速度）公式计算出为0.1。相应的得到表征流体可压缩程度的无量纲参数，即马赫数（其中max为最大格子速度）为0.02，远小于0.3，满足低马赫数要求。

1.2.3 CFD方法设定

CFD模拟通过采用基于有限体积法的商业软件FLUENT15.0。采用三维双精度模型，网格划分采用软件Gambit2.4.6。划分后的网格为非结构化网格，网格数量为43 000个。CFD的时间步长设置为0.000 1 s，各速度分量的残差为1×10-5m/s。入口边界条件为速度边界条件，大小为1.5 m/s，出口边界条件为大气压。模型为湍流模型K-epsilon模型，考虑到与LBM计算结果对比，选择非稳态计算。模型由6个单元组成，如图3所示，第3个单元用来作为与LBM计算结果，以及和PIV试验结果对比的单元。为定量化对比和分析，选择此单元空间线上的流速进行对比，线的位置如图4a所示。本文的数据曲线后处理软件为OriginPro2016，数据图后处理软件为ParaView5.1.2。

1.3 PIV测试

本试验的试验件材料为有机玻璃，加工方法为精雕刻，其流道尺寸按1∶1加工。试验测量的单元为图3结构中从左向右第3个单元。测量平面为图4a所示的水平截面，截面位于流道深度中间层。标号1为入口，标号2为出口，其特征尺度为1 mm。测量线为线，线长为1 mm，距离入口1的距离为0.7 mm。测量线位于水平截面上。图4b为分流式灌水器的关键尺寸，收缩段宽为0.8 mm，喉部宽为0.7 mm，倾斜角为60°，分流段宽为0.65 mm。流道入口出口宽度为1 mm，流道深度为0.8 mm。

试验采用PIV进行可视化试验。可视化试验台包括以下组成部分：1）被测的透明的灌水器试验件和用于固定试验件的固定台；2）调节拍摄区域的固定支座；3）照亮被测区域的光源系统，一般为脉冲激光；4）由CCD（charge coupled device）相机，CCD镜头以及光学镜头过滤器组成的图像采集系统；5）用于提供额定压力供水的水泵。同时需要1台安装有合适的图像分析软件的计算机。流速分布可视化试验台及其组成结构如图5所示。

速度分布可视化系统采用荧光粒子作为示踪粒子，其密度约为0.95～1.05 g/cm3，粒径为2～10m，与试验用的普通水密度相近，粒子的材料为聚苯乙烯；光源系统为Dual Power高能量双腔的激光器，满足试验激发荧光示踪粒子的要求；采用DANTEC公司的14位的Flow Sense EO 4M CCD相机作为图像采集系统，跨帧时间可以为200 ns，可以更好获得速度矢量分布；图像处理与分析软件采用Dynamic Studio图像系统平台，使用adaptive correlation算法分析流场，获得速度分布。

2 结果与分析

2.1 LBM网格无关性分析

LBM模拟结构的整体尺寸以及不同网格分辨率下对应的格子尺寸如表1所示。与有限体积法求解器中不同的是，LBM高网格分辨率对应着细小的格子尺寸，但同时也必须通过调整松弛时间来减小时间步长。

按照不同网格分辨率，对测量线上的流速进行了计算和对比，如图6所示。由图6a可以看出，网格分辨率为200的流速曲线明显与网格分辨率为400和500时存在明显的差异，表明网格分辨率太低可造成较大的误差。图6b和图6c进一步分别对比了不同网格分辨率下的方向与方向流速分量，可以得出，网格分辨率为400与500情况下的流速曲线趋向于吻合。又考虑计算的时间效率，确定分辨率为400。

2.2 LBM和CFD与PIV试验结果的对比分析

图7为0.82 s时基于LBM 计算的流速迹线图，图中在分流口处存在明显的流速变化，此处的流速值相比其他地方较大。图8对比了PIV与LBM以及CFD的云图结果，图中显示的结果为图4中所示的截面所在层的流场的速度云图。由图8可以看出，LBM计算的结果与PIV以及CFD计算的结果相对吻合：在双通流道中的第1个拐角处，流速梯度明显增大，最大值为1.037 m/s。同时在尾部出口，都有1个缓慢增长的流速，同时在双通道中的下通道中，明显存在低速区，便于水沙分流。

图9为测量线上PIV试验与仿真结果的对比曲线。对比结果可以得出，LBM与CFD流场曲线具有一致的方向，尽管在流速最大处，CFD的计算结果略高于LBM计算结果，但两者具有相同的位置点。同时，CFD与LBM在曲线末端有更好的一致性。与PIV试验结果对比，在起始和末尾处，CFD与PIV试验结果更接近，但在中间阶段，CFD的计算结果与PIV的结果存在正负变化的偏差。距离0.482 mm处，PIV测试结果为1.09 m/s，CFD达到最大流速1.176 m/s，LBM也达到最大流速1.06 m/s。在0.482 mm处，与PIV结果相比，CFD的相对误差为7.8%，明显大于LBM的相对误差2.7%。

对数据点进行了多项式拟合，拟合曲线方程为=Intercept+1·1+2·2+3·3+4·4+5·5+6·6+7·7+8·8+9·9（为距离，mm；为流速，m/s），其拟合方程的各参数值如表2所示。不同方法拟合曲线的2均大于0.99。从拟合相对误差（原始数据值与拟合值的差值除以原始值，如图10a所示）分布看，最大相对误差均小于5%，可见多项式拟合结果能较好地描述流速随距离的变化。

分别求LBM与CFD拟合曲线偏离PIV拟合曲线的相对偏差，如图10b所示。采用相对误差的算术平均值（图10b中灰色面积与黑色面积分别除以统计点的个数）定量评价2种数值计算结果偏离PIV试验结果的程度，如表3所示。

表2 拟合方程的系数值

由表3可以看出，LBM偏离试验的相对偏差的算术平均值（0.115%）略低于CFD偏离试验的相对偏差的算术平均值（0.139%）。但两者都在同一个数量级上，并且相差很小。由以上结果可以看出，尽管采用基于连续性介质假设下的CFD方法计算的结果整体比LBM计算结果偏大，但两者相对PIV试验结果的相对偏差的算术平均值基本相同，因而针对流道尺度范围在几百到1 000m的灌水器，采用基于连续性介质假设下的CFD计算方法是适用的。

3 结论与讨论

常规的灌水器研究手段通常是直接采用连续性介质假设下的宏观方法进行研究，而对宏观方法在灌水器这种微流道研究中的适用性未进行论证。本文采用介观的研究方法—格子Boltzmann方法（Lattice Boltzmannmethod, LBM）检验基于连续性假设下的数值计算方法在灌水器流道设计中的适用性。首先通过网格无关性分析确认了计算网格，从而保证计算结果的数值精度；然后通过对比指定截面上的流场云图，定性地对比了LBM与CFD以及PIV试验的结果，最后通过对比流速波动显著位置处的流速值定量分析了LBM与CFD分别与PIV试验结果。结论表明，CFD偏离PIV试验的相对偏差的算术平均值为0.139%，而LBM偏离PIV试验的相对偏差的算术平均值为0.115%。两者偏离PIV试验的相对偏差的算术平均值比较接近。因此，针对流道特征尺寸为1mm的灌水器，采用基于连续性介质假设下的流体动力学计算方法来研究是适用的。

目前大量关于灌水器的数值研究手段主要是通过直接采用基于连续介质假设下的宏观流体力学方法来进行流场分析，尽管已有学者提出这种方法在灌水器微流道设计中的适用性疑问，但未曾有人做过研究。随着低能耗小流量滴灌的发展，灌水器流道的特征尺寸也越来越小，因而传统的设计方法是否适用，更需要进一步验证。本文通过采用微流体研究方法—格子Boltzmann方法验证了流道特征尺度为1mm时，基于连续介质假设下的宏观流体力学方法依然适用。本文的不足之处是未对压力场、涡量场等进行试验和对比分析。目前，国内滴灌灌水器设计理论研究急需解决的问题为建立灌水器流道内部微流体流动机理的系统的研究方法，对比分析与宏观流动中流体特性以及影响流动特性的因素的变化，提供微流道内流场的系统的研究方案。

[1] 黄兴法，李光永. 地下滴灌技术的研究现状与发展[J]. 农业工程学报，2002，18(2)：176－181.

Huang Xingfa, Li Guangyong. Present situation and development of subsurface drip irrigation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2002, 18(1): 176－181. (in Chinese with English abstract)

[2] 金文，张鸿雁. 灌水器内流道流场Micro-PIV试验分析[J]. 农业工程学报，2010，26(2)：12－17.

Jin Wen, Zhang Hongyan. Micro-PIV analysis of flow fields in flow channel of emitter[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(2): 12－17. (in Chinese with English abstract)

[3] 魏正英，赵万华，唐一平，等. 滴灌灌水器迷宫流道主航道抗堵设计方法研究[J]. 农业工程学报，2005，21(6)：1－7.

Wei Zhengying, Zhao Wanhua, Tang Yiping, et al. Anti-clogging design method for the labyrinth channels of drip irrigation emitters[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2005, 21(6): 1－7. (in Chinese with English abstract)

[4] 田济扬，白丹，于福亮，等. 基于Fluent软件的滴灌双向流流道灌水器水力性能数值模拟[J]. 农业工程学报，2014，30(20)：65－71.

Tian Jiyang, Bai Dan, Yu Fuliang, et al. Numerical simulation of hydraulic performance on bidirectional flow channel of drip irrigation emitter using Fluent[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(20): 65－71. (in Chinese with English abstract)

[5] 田济扬，白丹，任长江，等. 滴灌双向流流道灌水器水力特性分析[J]. 农业工程学报，2013，29(20)：89－94.

Tian Jiyang, Bai Dan, Ren Changjiang, et al. Analysis on hydraulic performance of bidirectional flow channel of drip irrigation emitter[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(20): 89－94. (in Chinese with English abstract)

[6] 魏正英，唐一平，温聚英，等. 灌水器微细流道水沙两相流分析和微PIV及抗堵实验研究[J]. 农业工程学报，2008，

24(6)：1－9.

Wei Zhengying, Tang Yiping, Wen Juying, et al. Two-phase flow analysis and experimental investigation of micro-PIV and anti-clogging for micro-channels of emitter[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2008, 24(6): 1－9. (in Chinese with English abstract)

[7] 张俊，赵万华，粟晓玲，等. 微灌长流道灌水器结构特性的研究综述[J]. 农业工程学报，2005，21(1)：182－185.

Zhang Jun, Zhao Wanhua, Su Xiaoling, et al. Review of structural characteristics analysis of the long-path emitter s for micro irrigation [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2005, 21(1): 182－185. (in Chinese with English abstract)

[8] 郭霖，白丹，王新端，等. 双向对冲流滴灌灌水器水力性能与消能效果[J]. 农业工程学报，2016，32(17)：77－82.

Guo Lin, Bai Dan, Wang Xinduan, et al. Hydraulic performance and energy dissipation effect of two-ways mixed flow emitter in drip irrigation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(17): 77－82. (in Chinese with English abstract)

[9] 李云开，杨培岭，任树梅. 滴灌灌水器流道设计理论研究若干问题的综述[J]. 农业机械学报，2006，37(2)：145－149.

Li Yunkai, Yang Peiling, Ren Shumei. General review on several fundamental points of design theory about flow path in drip irrigation emitters[J]. Transactions of the Chinese Society for Agricultural Machinery, 2006, 37(2): 145－149. (in Chinese with English abstract)

[10] 李云开，冯吉. 滴灌灌水器内部水动力学特性测试研究进展[J]. 排灌机械工程学报，2014，32(1)：86－92.

Li Yunkai, Feng Ji. Progress in measurement of hydrodynamic characteristics in drip irrigation emitters[J]. Journal of Drainage and Irrigation Machinery Engineering. 2014, 32(1): 86－92. (in Chinese with English abstract)

[11] 张俊. 迷宫流道灌水器水力与抗堵性能评价及结构优化研究[D]. 西安：西安交通大学，2009.

Zhang Jun. Evaluation of Hydraulic and Anti-clogging Performances and Structural Optimization of Labyrinth-Channel Emitters[D]. Xi’an: Xi'an Jiaotong University, 2009. (in Chinese with English abstract)

[12] Mala G M, Li Dongqing. Flow characteristics of water in microtubes[J]. International Journal of Heat and Mass Transfer, 1999, 20(2): 142－148.

[13] Qu Weilin, Mala G M, Li Dongqing. Pressure-driven water flows in trapezoidal silicon microchannels[J]. International Journal of Heat and Mass Transfer, 2000, 43(3): 353－364.

[14] Eringen C A. Simple micro-fluids[J]. Engineering Science, 1964, 2: 205－217.

[15] Ariman T, Turk M A, Sylvester N D. Microcontinuum field mechanics: A review[J]. Engineering Science, 1973, 11(8): 905－930.

[16] Tuckermann D B, Pease R F. Optimized convective cooling using micromachined structures[J]. Journal of Electrochemiecal Society, 1981, 129(3): 98－100

[17] Harley J, Bau H, Zemel J, et al. Fluid flow in micron and submicron size channels[J]. Micro Electro Mechanical Systems, 1989, 12(3): 25－28.

[18] Choi S B，Barron R F and Warrington R O. Fluid flow and heat transfer in microtubes[J].ASME Proceedings, 1991(1), 32:123－134.

[19] Pfahler J N. Liquid Transport in Micro and Submicron Channels [D]. PA: University of Pennsylvania, 1992.

[20] Rahman M M, Gui F. Experimental measurements of fluid flow and heat transfer in microchannel cooling passagages in a drip substrate[J]. Advances in Electronic Packaging, 1993, 4(2): 685－692.

[21] Peng X F. Friction flow characteristics of water flowing through rectangular microchannels[J]. Exp Heat Transfer, 1994, 7(4): 249－264

[22] Peng X F, Peterson G P, Wang B X. Heat Transfer characteristics of water flowing through microchannel[J]. Experimental Heat Transfer, 1994, 7(4): 265－283.

[23] Peng X F, Peterson G P. Forced convection heat transfer of single phase binary mixtures through microchannels[J]. Experimental Thermal and Fluid Science, 1996, 12(1): 98－104

[24] McNamara G, Zanetti G. Use of the Boltzmann equation to simulate lattice-gas automata[J]. Physics Review letters, 1988, 61(20): 2332－2335.

[25] Qian Y H, D’Humières D, Lallemand P. Lattice BGK models for Navier-Stokes equation[J]. Europhysics Letters, 1992, 17(6): 479－486.

[26] Chen S Y, Doolen G D. Lattice Boltzmann method for fluid flows[J]. Annual Review of Fluid Mechanics, 1988, 30(1): 329－364.

[27] Succi S. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond[D]. Oxford: Oxford University Press, 2001.

[28] Nie Xiaobo, Doolen G D, Chen Shiyi. Lattice Boltzmann simulation of fluid flows in MEMS[J]. Journal of Statistical Physics, 2002, 107(1/2): 279－289.

[29] Chen Shiyi, Doolen G. Lattice Boltzmann method for fluid flows[J]. Annual Review of Fluid Mechanics, 2003, 30(1): 329－364.

[30] Aidun C K, Clausen J R. Lattice-Boltzmann method for complex flows[J]. Annual Review of Fluid Mechanics, 2010, 42(1): 439－472.

[31] Bhatnagar P L, Gross E P, Krook M. A model for collision processes in gases.I. Small amplitude processes in charged and neutral one-component systems[J]. Physics Review, 1954, 94(3): 511－525.

[32] 苑伟静，魏正英，楚华丽，等. 分流式灌水器结构优化设计与试验[J]. 农业工程学报，2014，30(17)：117－124.

Yuan Weijing, Wei Zhengying, Chu Huali, et al. Optimal design and experiment for divided-flow emitter in drip irrigation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(17): 117－124. (in Chinese with English abstract)

[33] Raabe D. Overview of the lattice Boltzmann method for nano- and microscale fluid dynamics in materials science and engineering[J]. Modelling and Simulation in Materials Science and Engineering, 2004, 12(3): 13－46.

Applicability on continuous medium hypothesis in design of emitter using PIV and LBM method

Ma Shengli, Wei Zhengying※, Zhang Yubin, Chen Xueli, Ma Chao

(710049,)

The characteristics of microfluidic devices are different from those of ordinary fluid devices. One of the most important features of microfluidic devices is the decrease of their characteristic scale. This feature leads to a lot of differences in microfluidic device. Two major differences are included. There are the flow law of the fluid and the physical properties of fluid. The flow law of the fluid in a microfluidic device is different from that in an ordinary fluid device. The physical properties of the fluid in a microfluidic device also differ from that in an ordinary fluid device. The emitter channel is small in size from the point view of its width. As a result, the emitter belongs to the microfluidic device. Therefore, the applicability of Navier-Stokes (NS) equations has been controversial in the analysis of the flow characteristics in the emitter channel. In order to verify the suitability of the continuity medium hypothesis in design of the emitter, the lattice Boltzmann method (LBM) was used to study the flow characteristics of the emitter in this paper. The flow rate field on a specific plane obtained by different numerical methods was analyzed. The numerical methods were LBM and the computational fluid dynamics (CFD) method which was based on the finite volume method. The flow rate field obtained by using the two numerical methods was also compared with the experimental results. The flow rate with larger flow rate gradient of the straight line on the specific plane was also compared and analyzed. Firstly, the mesh independent analysis was made in order to guarantee the numerical accuracy of numerical results. Secondly, the numerical results were compared with those obtained by the finite volume method (FVM) based on the assumption of continuous medium. The numerical results were also made a comparison with the particle image velocimetry (PIV) experimental results. The average relative deviations of the results of the LBM calculation from the experimental values of PIV were analyzed. In addition, the average relative errors of the results of the FVM calculation from the experimental values of the PIV were also analyzed. By comparing flow rate contours, the results showed that the overall flow rate field calculated by the LBM in the specified cross section was in good agreement with the flow rate field measurement by the experiment, and the results also showed that the flow rate field calculated by the CFD method in the specified cross section was in good agreement with the flow rate field measurement by the experiment. The flow rate contour which was calculated by the LBM or CFD showed a large flow rate gradient at the corner of the contraction section. Comparing the flow rate on the specified measurement line, CFD reached its maximum flow rate on the measurement line where the distance was 0.482 mm, and the flow rate obtained by using the computational fluid dynamics method which was based on the finite volume method was 1.176 m/s. The flow rate of PIV experimental results was 1.09 m/s. The flow rate obtained by using the LBM reached its maximum value, and the result of the flow rate obtained by using the LBM was 1.06 m/s. Therefore, the relative error of flow rate obtained by using the CFD from the experimental result at 0.482 mm was 7.8%, which was larger than that of LBM which had the relative error of 2.7%. In view of the arithmetic mean of the relative deviation, the results showed that the arithmetic mean of the relative deviation of the CFD deviation from the PIV experiment was 0.139%, while the arithmetic mean of the relative deviation of LBM deviation was 0.115%. The results were very close. Therefore, the computational fluid dynamics method based on the assumption of continuous medium is applicable for analysis of the flow field in the emitter which has the characteristic size of 1 mm.

computational fluid dynamics; Boltzmann equation; flow rate; particle image velocimetry; continuous medium hypothesis; LBM; emitter

10.11975/j.issn.1002-6819.2017.09.012

S275.6

A

1002-6819(2017)-09-0092-07

2016-09-13

2017-04-06

国家科技支撑计划项目（2015BAD24B01）；国家重点研发计划项目（2016YFC0400201）

马胜利，男，陕西西安人，博士，主要从事灌水器研究。西安 西安交通大学机械工程学院，710049。Email：mashengli1987@163.com

魏正英，女，陕西西安人，教授，博士生导师，主要从事微细产品结构设计和快速制造技术研究。西安 西安交通大学机械工程学院，710049。Email：zywei@mail.xjtu.edu.cn

马胜利，魏正英，张育斌，陈雪丽，马 超. 用PIV和LBM法检验灌水器设计中连续介质假设的适用性[J]. 农业工程学报，2017，33(9)：92－98. doi：10.11975/j.issn.1002-6819.2017.09.012 http://www.tcsae.org

Ma Shengli, Wei Zhengying, Zhang Yubin, Chen Xueli, Ma Chao. Applicability on continuous medium hypothesis in design of emitter using PIV and LBM method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(9): 92－98. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.09.012 http://www.tcsae.org