考虑灌溉参数空间变异的区域畦灌模拟与验证
董勤各,许 迪,章少辉,白美健,李益农
考虑灌溉参数空间变异的区域畦灌模拟与验证
董勤各1,2,许 迪3※,章少辉3,白美健3,李益农3
(1. 西北农林科技大学水土保持研究所,杨凌 712100;2. 中国科学院水利部水土保持研究所,杨凌 712100;3. 中国水利水电科学研究院流域水循环国家重点实验室,北京 100038)
精确评估区域畦田灌水质量有助于提高农田灌水管理水平,而具有空间变异性的灌溉参数如何有效表征是影响区域畦田灌水质量精确模拟评价的关键因素。为此,该研究的目的在于借助Monte-Carlo抽样,建立考虑畦灌参数空间变异性的区域畦灌模拟方法。采用Monte-Carlo抽样将具有空间变异性的区域灌溉参数(如入畦单宽流量、土壤砂粒含量、黏粒含量、土壤容重等)离散表征为若干个灌溉参数样本,依次输入田块尺度畦灌地表水流-土壤水动力学耦合模型,以模拟评价区域畦灌过程。基于3次区域畦灌试验的实测数据和1个对比的确定性畦灌模拟方法,验证建立的模型的模拟效果。结果表明,所建模拟方法与确定性模拟方法模拟计算的灌水效率和灌水均匀具一定差异,所建模型的模拟值与实测值间的灌溉定额和田间水利用系数相对误差分别为9.95%~12.23%和8.39%~10.21%,而基于现有模型的相对误差则分别为14.15%~16.78%和13.87%~15.88%,畦田平均土壤含水率实测值与所建模型模拟值的累积分布趋势表现出良好的一致性。上述指标表明所建模拟方法有效缩小了区域灌溉参数空间均化处理所带来的模拟误差范围较大等问题,为区域畦田灌溉优化设计和管理提供了技术支撑。
灌溉;Monte-Carlo方法;土壤; 参数;空间变异;灌水质量;数值模拟
0 引 言
畦田灌溉运行管理简单、省时节力成本低,占据着中国农业灌溉方式的主导地位[1]。精确模拟评价畦田灌水质量,对提高农业用水管理水平、促进灌溉农业的可持续发展具有重要意义。基于物理机制的畦灌模拟模型(如WinSRFR与B2B等)已在畦灌过程模拟与灌水质量评价方面得到广泛应用[2-3]。这些畦灌模拟模型多用于模拟单个田块灌溉过程[4-7],难以描述区域畦灌参数空间变异下的灌溉水流动态变化规律,致使畦灌模拟评价往往存在难以解释的误差。针对土壤特性、入畦单宽流量、田面糙率、田面微地形等灌溉参数区域空间变异性的处理方式,区域农田水文过程模拟模型可分为3类:1)确定性模拟模型。该类模型主要将灌溉参数在区域尺度上均化处理,得到1组确定性灌溉参数值,输入田块尺度农田水文模拟模型进行模拟计算[8-9];2)分布式模拟模型。该类模型将模拟区域划分为若干子区域,对子区域内灌溉参数加权平均,并依次将所得灌溉参数值输入给田块尺度农田水文模型,然后对上述模拟数据依据子区域面积进行加权计算,实现对区域农田水文过程的有效模拟[10-12];3)空间随机模拟模型。该类模型借助参数随机抽样方法,充分表征灌溉参数的区域空间变异性,然后将抽取的灌溉参数值依次输入给田块尺度农田水文模型,对模拟数据进行同系数加权计算,以模拟区域农田水文过程[13]。确定性模拟与分布式模拟均难以精确描述灌溉参数空间变异性对区域灌溉过程及灌水质量的影响,且分布式模拟易导致子区域灌溉参数值被过高或过低估计[8-12],严重影响模拟精度;参数随机模拟能有效避免上述问题,然而鲜见其用于区域畦灌过程模拟方面的报道。
Monte-Carlo抽样是一种以概率统计理论为主要理论基础的参数随机模拟方法,能够避开研究对象复杂内部特性描述及其在系统行为上的困难,直接以系统运用过程模拟替代系统分析,便于解决那些由于计算过于复杂而难以得到解析解或者根本没有解析解的问题[14-17]。因此,针对现有灌溉模型参数过于受到人为因素干扰,而未能很好表征区域畦灌参数的空间变异性,从而影响模拟精度等问题,本文以已有的畦灌地表水流-土壤水动力 学耦合模拟模型为工具[7-8],借助Monte-Carlo抽样,建立考虑畦灌参数空间变异性的区域畦灌模拟方法(stochastic parameter irrigation model,SRM)。基于在山东麻湾灌区开展的3次区域畦田灌溉试验,对模型的模拟效果进行验证,以期为区域畦田灌溉优化设计和管理提供技术支撑。
1 考虑灌溉参数空间变异的区域畦灌模拟
1.1 模型假设
本文建立的考虑灌溉参数空间变异性的区域畦灌模拟方法主要包括2个部分,即畦灌地表水流-土壤水动力学耦合模拟与灌溉参数的Monte-Carlo抽样。为简化区域畦灌模拟过程,特假设如下:1)单个田块内土壤质地均匀,考虑到区域内农田耕作与管理措施相同,坡度可视为一致;2)畦田长宽比较大,地表水流横向运动过程远远小于沿畦长方向的纵向运动过程,一般将畦灌地表水流为沿畦长方向的一维运动过程;3)由于土壤沿畦长方向的水平入渗速率远远低于地表水流运动速度,导致土壤垂向入渗占主导地位,故只模拟土壤垂向入渗过程;4)只模拟田块内畦灌水流过程,不涉及渠系水流过程,且田块间水流通量忽略不计。
1.2 畦灌地表水流-土壤水动力学耦合模拟
本文采用一维畦灌地表水流运动模型模拟畦灌地表水流运动过程、一维土壤水动力学模型模拟灌溉水流入渗过程及土壤水再分布过程。一维畦灌地表水流运动模型采用基于有限差分法、有限体积法与有限单元法建立的混合数值方法解算,一维土壤水动力学模型采用高精度有限体积法与有限差分格式解算,具体解算过程详见文献[7,18]。
1.2.1 控制方程
单个田块的畦灌地表-土壤水流运动过程可采用由一维地表水流运动模型和一维土壤水动力学模型耦合构建的田块尺度畦灌数值模型描述[7-8]。在假设单个畦田的土壤质地均匀分布基础上,畦灌一维地表水流运动控制方程的矢量形式可表达如下
U+F=1+2+3(1)
式中U是因变量矢量;F是物理通量;1是畦面糙率;2和3分别是地形项和入渗项,分别用于描述畦田微地形状况及土壤特性对畦灌水流运动的影响。
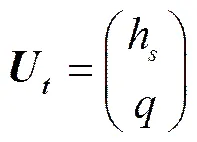
,,(3)
式中h为地表水深,m;为单宽流量,m3/(s·m);为入渗率,可通过式(4)计算土壤水分单位时间变化量获得,m/s;为重力加速度,m/s2;为水流推进距离,m;z为地面高程,m;为时间,s;为曼宁糙率系数,m1/6;为垂直平均流速,m/s。
畦灌时地表水流沿畦长方向运动速度远大于地表水流入渗后形成的土壤水流水平运动速度,且地表水流沿畦长方向推进的同时还垂向入渗土壤,故畦灌时土壤水流沿畦长方向运移的湿润锋位置取决于地表水流的推进锋位置,则土壤水平入渗过程可忽略,仅考虑垂向入渗过程[4,7]。同时,根据试验观测发现,单个田块畦灌过程约为0.5~1.5 h,一次区域畦灌过程约为3 d。可见,灌溉过程持续时间短、灌溉水流入渗及再分布过程在此期间受冬小麦根系吸水过程影响小,可忽略不计。因此,可将畦灌土壤水运移简化成不考虑作物吸水过程的一维非饱和土壤水动力学问题。
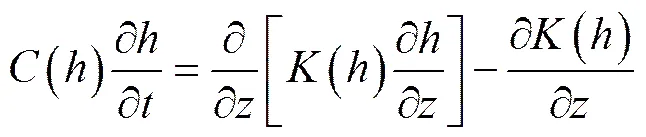
式中为土壤压力水头,入渗模拟时可用h代替,cm;为垂向距离,向下为正,cm;()为土壤非饱和导水率,cm/min;()为比水容量;为时间,min。
式(4)中的()和()可分别表示如下
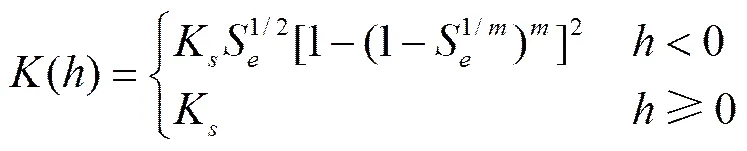
(6)
(7)
式中K为土壤饱和导水率,cm/min;S为土壤有效饱和度[7];、和均为土壤水分特征曲线参数,=1−1/;θ和θ分别为土壤残余及饱和含水率,cm3/cm3;为压力水头,cm;()为土壤含水率,cm3/cm3,其与关系采用van Genuchten模型[4](VG模型)表达如下

1.2.2 初始与边界条件
地表水流初始条件为畦田内地表水深和平均均为0,即h=0和=0。边界条件为:当畦首处于入流状态时,给定单宽流量=0(0为灌溉开始后的入畦单宽流量);灌水停止后,畦首单宽流量=0,由于灌溉地表水流始终处于亚临界流状态,故畦首水深值由畦内水深值插值获得。此外,当畦尾处于封口状态时,=0;若畦尾处于敞口状态,则依据灌溉水流始终处于亚临界流状态的物理事实[19],采用畦内单宽流量和水深值插值获得畦尾单宽流量和水深h值。
土壤水流初始条件为
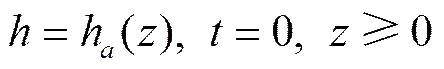
式中h()为土壤初始负压水头分布。
边界条件包括上边界条件与下边界条件。当畦灌强度(单位面积单位时间上畦田灌溉水深)大于土壤入渗能力时,产生地表积水或径流,此时上边界条件为
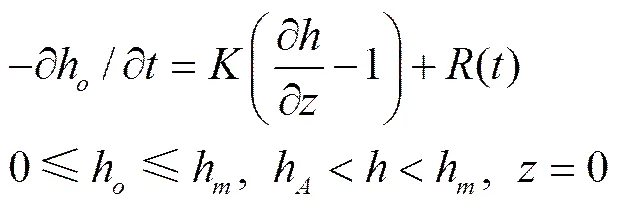
式中h为地表积水深度,其值为100h,cm;()为时刻的地表蒸发强度与畦灌强度之差,cm/min;h为地表最大积水深度,cm;h为土壤表层初始压力水头,cm;其他符号物理意义同上。
当地下水位较深时,下边界可采用自由排水条件
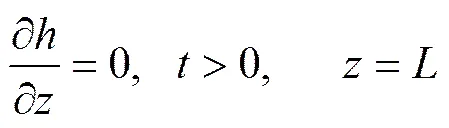
式中为下边界深度,cm。冬小麦根系主要集中在0~100 cm土层内,故取值为100 cm。
1.3 考虑空间变异性的畦灌参数随机模拟
1.3.1 区域畦灌参数的统计分析
在上述一维畦灌地表水流-土壤水动力学耦合模型中,将畦田长度、入畦单宽流量、土壤水力特性、畦田微地形状况作为初始与边界条件输入模型。由于土壤水力特性与土壤特性(如土壤砂粒、黏粒含量和有机质含量)呈非线性函数关系,故可由土壤砂粒、粉粒、黏粒和有机质含量耦合表达。在评价区域畦田灌水质量过程中,由于土壤特性、入畦单宽流量、田块规格等均具有空间不确定性特征,诸多学者常采用正态分布或对数正态分布描述其分布规律[13,20-22]。区域尺度上,畦田长度、畦田宽度、入畦单宽流量、土壤砂粒、粉粒、黏粒和有机质含量均呈现近似正态分布特征[20]。正态分布的概率分布函数为
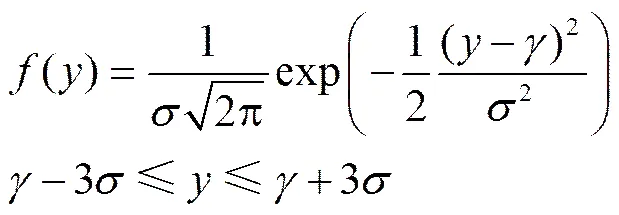
式中为随机变量;为随机变量的均值;为随机变量的标准差。利用Monte-Carlo随机生成的任意1组灌溉参数样本的值域范围通常在[–∞,+∞]之间,但由于农田生产活动和灌溉管理的要求,灌溉参数值域范围是有限的,而且与参数的标准偏差值密切相关。为了真实反映灌溉参数的变化幅度范围,需对随机生成的参数值域范围进行必要的限制。从实际意义和数学角度考虑,区域畦灌灌溉参数的值域范围可限制在[–3,+3]之间[23],这是由于该范围为置信水平为95%以上的置信区域。
畦田微地形状况包括畦田微地形起伏幅度及起伏位置空间分布[22]。由于相同耕作措施下的区域畦田微地形起伏幅度具有相似性,故量化畦田微地形起伏幅度的田面相对高程标准差可近似相同。然而,相同标准差下的畦田微地形起伏位置空间分布并非唯一,其差异性对灌水质量存在影响,需考虑多个畦田微地形起伏位置空间分布状况表征区域尺度上的畦田微地形状况[22]。用于表征畦田微地形状况的田面相对高程呈现近似正态分布特征[12]。
1.3.2 Monte-Carlo模拟
Monte-Carlo模拟以概率统计理论为基础[23],可用来分析各种不确定性问题。它假定随机变量的概率分布函数是已知的,通过随机抽样方法得到随机变量的若干个离散样本,通过数值模拟得到相应的输出结果,通过对输出结果的统计,得到均值、方差等估计量,并拟合其输出结果的概率分布特征。畦田灌水质量受畦田长度、入畦单宽流量、土壤特性、畦田微地形状况等灌溉参数约束。
本文假定区域畦田内的坡度、田面糙率与微地形标准差为常值,土壤特性、畦田长度、入畦单宽流量、畦田微地形状况的空间变异性是影响灌水质量优劣的重要因素。具体模拟流程如下:1)根据拟合统计得到的畦田长度、入畦单宽流量概率分布函数进行随机抽样,获得表征两者空间变异性的区域离散样本;2)根据拟合统计得到的土壤粉粒、黏粒及容重的概率分布函数,对上述变量进行随机抽样,并将随机抽取的样本输入Rosetta人工神经网络模型[24-25],转换为模型所需的土壤水力特性参数(饱和含水率θ、残余含水率θ、饱和导水率K、参数、);3)通过畦田长度、宽度及田块尺度畦灌模型地表单元格长度,计算田面相对高程数量,借助田面微地形随机模拟模型[22],获得田面相对高程序列,并对其沿畦宽方向做均化处理与统计特征修正,作为一个畦田微地形状况样本输入给田块尺度畦灌数值模型;4)重复上述步骤,获得由畦田长度、入畦单宽流量、土壤水力特性及畦田微地形状况组成的样本,依次输入畦灌地表水流-土壤水动力学耦合模型进行模拟;5)基于上述模拟结果,计算灌水质量评价指标,评价区域畦田灌水质量。区域畦灌随机模拟模型的构建流程如图1所示。
1.3.3 灌水质量评价指标
本文采用灌水效率与灌水均匀度作为灌水质量评价指标[26-27]。灌水效率通常是指1次灌水存储在作物根区的平均水深和畦田平均灌水深度之比。灌水均匀度是反映灌水沿畦田长度方向的入渗分布均匀程度。灌水均匀度越大,田块内各点土壤储存水分的均匀性就越好。
灌水效率E的计算公式如下[27]:
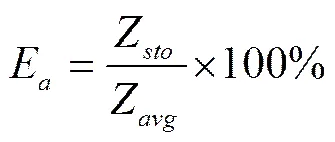
(14)
式中Z为灌溉后储存在作物根区的平均水深,cm;Z为单个田块平均灌水深度,cm;θ和θ分别为灌前和灌后计划湿润层内平均土壤体积含水率,cm3/cm3;R为作物根区深度,依据实测情况取值为100 cm。
灌水均匀度C的计算公式如下[27]
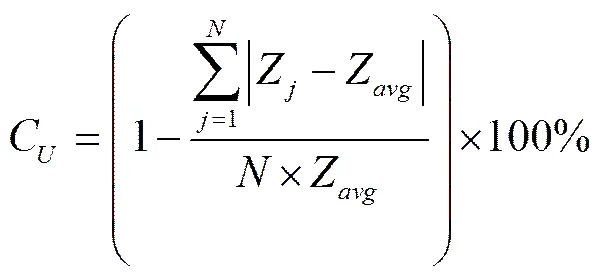
式中C为灌水均匀度,%;Z为第个测点灌水深度,cm;为单个畦田沿畦长方向的测点数。
1.3.4 数据分析与处理
通过Monte-Carlo抽样与畦灌地表水流-土壤水动力学耦合模型的模拟计算,针对抽样得到的每组输入值,统计分析模拟输出数据,计算灌水质量评价指标。由于一维畦灌地表水流-土壤水动力学耦合模型的输出为单个田块的畦灌过程数据,而输入不确定性为具有空间随机性的土壤特性、畦田长度、入畦单宽流量与畦田微地形等灌溉参数。因此,为表征区域尺度畦灌参数不确定性的影响,本文采用累积概率分布及经典统计方法,验证考虑畦灌参数随机模拟的区域畦灌模拟方法。
2 区域畦灌试验与模型参数选取及样本量确定
2.1 区域畦灌试验
2.1.1 试验区与观测指标
田间试验在山东东营市麻湾灌区开展(118°22′E,37°12′N),试验区面积76 hm2,包括272块畦田。麻湾灌区地处黄河下游滨海地区,属暖温带季风型大陆性气候,多年平均降水量为537.4 mm。试验区内0~100 cm土层以黏壤土为主。主要种植作物为冬小麦和夏玉米。该灌区主要在冬小麦越冬期前(11月)、返青-拔节期(3月)和抽穗-灌浆期(5月)进行灌溉,补充作物所需水分。一般采用条畦灌溉方式,水源为黄河引水。由于冬小麦灌浆期植株过高过密,不利于精确观测水流推进过程和畦面微地形状况,因此,分别选在2012年3月(T1),2012年11月(T2),2013年3月(T3)开展3次冬小麦区域畦灌试验,以验证所建区域畦灌模拟方法的准确性。
畦灌前,采用工程测量绳测定272块畦田的长度与宽度;利用自动对焦水准仪(苏州一光仪器有限公司,±1.0 mm)观测选取的100块畦田的相对高程。畦灌时,观测100块畦田的水流推进过程和入畦流量,水流推进到畦尾后关闭进水口,便携式自动流量计(上海安钧电子科技有限公司,±1%)测定入畦流量。灌前1 d与灌后2 d,在随机选取的100块畦田的畦首、畦中与畦尾处,均沿地面垂向分4层(0~20 cm、>20~40 cm、>40~70 cm及>70~100 cm)采集土样测定土壤含水率,其中采用畦田中部前3层土样测定土壤颗粒组成、容重和有机质含量。采用比重计法测定土壤颗粒组成,重铬酸钾法测定土壤有机质含量,烘干法测定土壤容重和土壤含水率[28]。
2.1.2 区域畦灌参数统计特征
畦田灌水质量主要受畦田长度、田面微地形状况、土壤特性与入畦单宽流量等灌溉参数影响。根据研究区内畦田分布与耕作管理特性,畦田长度表现出相对稳定的特征,其概率分布特征如图2a所示。拟合统计可以看出,研究区内畦田长度基本呈现正态分布特征,其概率密度函数可采用正态分布函数来拟合,拟合分布模型如式(12)所示。畦田长度正态拟合的参数有2个:均值120 m,标准差33.6 m。研究区内畦田宽度具有一定的空间随机性(图2b),呈现近似正态分布统计特征,其拟合分布模型如式(12)所示,对研究区内畦田宽度拟合,均值9 m,标准差1.98 m。考虑到模型模拟时采用的是入畦单宽流量,基于观测的入畦流量以及畦田宽度数据,计算每块畦田的入畦单宽流量。表1给出入畦单宽流量的统计特征和K-S检验结果,可以看出,3次试验的入畦单宽流量平均值的变化很小,但相应的标准差变化幅度较大;经Kolomogorov-Smirnov方法(K-S)检验[29],入畦单宽流量呈现明显的正态分布统计特征。

表1 麻湾灌区试验区土壤容重和有机质及单宽流量的统计特征及K-S检验结果
注:N为正态分布,下同。
Note: N is normal distribution, the same as below.
研究区采用相似的农田耕作管理方式,随机选取的100块畦田的田面相对高程的标准差比较一致。3次试验的田面相对高程标准差的均值及其标准差分别为4.06、4.23、4.17 cm与0.12、0.15、0.14 cm,畦面坡度均近似为0.6‰,田面相对高程空间变异特征参数均值如表2所示,可用于模拟田面微地形。由于畦灌地表水流-土壤水动力学耦合模型为沿畦长方向的一维数值模拟,因此需要对通过田面微地形随机模拟模型[22]生成的田面相对高程数据沿畦宽方向做均化处理。
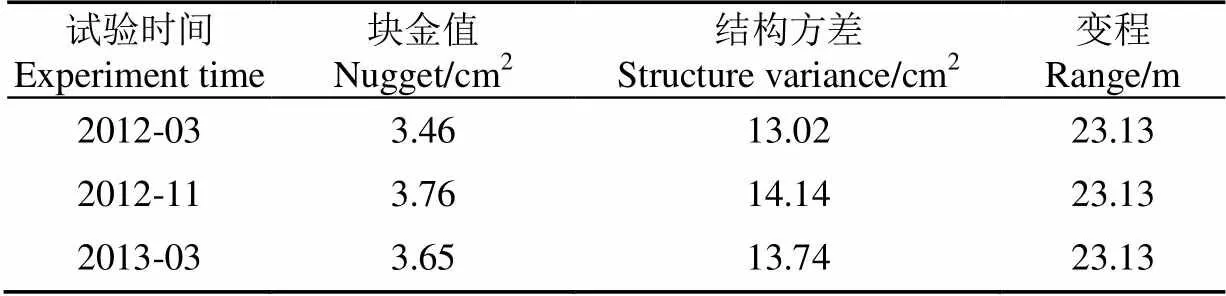
表2 麻湾灌区田面相对高程空间变异特征参数
土壤特性主要包括土壤质地、容重及有机质含量。根据测定的土壤质地、容重与有机质含量数据,分别统计其概率分布特征。经K-S检验,试验区内每层土壤的砂粒、粉粒、黏粒含量均呈现明显的正态分布统计特征,分布模型如式(12)所示。3次试验测定发现,土壤质地统计特征值基本一致,故本文采用2012年3月试验的数据统计指标(表3)随机抽取土壤质地样本。3次试验的土壤容重均呈现明显的正态分布统计特征,主要参数如表1所示。3次试验的土壤有机质含量均值与标准差比较一致,均呈现正态分布特征(表1)。

表3 麻弯灌区土壤颗粒组成的统计特征及K-S检验结果
依据美国农业干旱研究中心研究成果,畦灌过程中田面糙率系数一般可参照作物长势获得[30-31],故通过参考其提供的基于冬小麦生育期长势确定的田面糙率系数数据库,将麻湾灌区3次试验的田面糙率系数分别设为0.13、0.09和0.14。
2.2 畦灌参数选取及参数样本量确定方法
模型的输入参数包括畦长、田面微地形状况、入畦单宽流量、灌水时间、地表糙率系数和由土壤特性参数推求的VG模型参数(θ、θ、K、、)。畦长取实测值均值作为模型输入参数;入畦单宽流量通过Monte-Carlo抽样获得;土壤水力特性参数由Monte-Carlo抽取土壤砂粒、粉粒及容重样本后经Rosetta模型转换获得;田面微地形状况由修正的田面微地形随机模拟模型生成并修正后获得;3次试验的地表糙率系数,依据美国农业干旱研究中心研究成果分别设为0.13、0.09和0.14;依据当地农田灌水实际,水流推进到畦田尾部时关闭入水口。
采用Monte-Carlo抽样研究区域灌溉参数空间变异性时,需依据各参数的概率分布函数,随机抽取与研究区灌溉参数分布特征相一致的参数样本量。将抽取的随机样本作为畦灌地表水流-土壤水动力学耦合模型的输入条件。当随机抽取一定数量的随机参数组合样本后,需要解决的问题是,针对给定模型输入参数特征值,运行田块尺度畦灌耦合模型评价区域畦田灌水质量时,模拟多少组随机参数样本组合才能较真实表征实际区域畦灌过程、合理评价区域畦田灌水质量,这需要设定科学严谨的判断标准。在其他条件相同的情况下,给定的随机参数样本组合对应唯一的灌水效率E和灌水均匀度C。因此,从随机参数分布总体中抽取一定数量的样本作为代表,利用畦灌耦合模型进行畦灌模拟试验,借助式(16)、(17)与(18)统计分析若干参数样本条件下得到的区域畦田灌水质量评价指标,并得出可以反映随机参数分布总体对灌水质量影响的最小个体数量。当模拟次数达到一定数量后,畦田灌水质量评价指标值均值M和标准差R将趋于稳定。如果以连续6个数据点的M<0.5%和R<5%作为均值和标准差达到稳定状态的判别指标,则可确定灌水质量评价指标值均值及相应标准差。M和R的计算公式分别如下
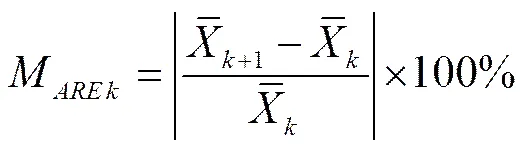
(17)
(18)
式中M为第+1个灌水质量评价指标值均值与第个的相对误差;R为+1个灌水质量评价指标值的标准差与个的相对误差;X+1为基于第+ 1个参数样本模拟计算的灌水质量评价指标值;为基于第1~个参数样本模拟计算的灌水质量评价指标值的均值;S为个灌水质量评价指标值的标准差;为灌水质量评价指标均值收敛时的模拟计算次数。
3 考虑灌溉参数空间变异的区域畦灌模型验证
3.1 对比的灌溉模拟方法
采用确定性模拟方法作为对比的灌溉模拟方法(deterministic parameter irrigation model,FIM),该方法是将模型输入参数在区域尺度上进行平均处理,其值输入给模型以进行模拟,并输出单一灌溉过程数据,仅能描述区域整体的静态灌溉特征。对现有模拟方法的改进,主要体现在模型输入参数值如何精确描述区域灌溉参数空间变异性的差异上。对比的确定性模拟方法的输入参数值如下:基于3次区域畦灌试验确定的畦田长度均为120 m;糙率系数分别为0.13、0.09、0.14;入畦单宽流量分别为3.12、3.24、3.16 L/(s×m);田面相对高程标准差的均值分别为4.06、4.23、4.17 cm(对应的空间特征变异参数见表2);VG模型参数θ分别为0.428、0.442、0.421 cm3/cm3,θ分别为0.071、0.073、0.070 cm3/cm3,K分别为0.013 3、0.018 0、0.011 5 cm/min,分别为0.005 3、0.005 1、0.005 4,分别为1.658、1.667、1.651;依据当地农田灌水实际,水流推进到畦田尾部时关闭入水口。模拟每个畦灌过程时,畦长方向和土壤垂向的空间离散步长分别取为2.0和0.01 m,土壤与地表水流时间离散步长均取值为1 s。
3.2 验证指标
选取灌溉定额、根系层土壤含水率均值与田间水利用系数作为验证区域畦灌模型模拟精度的评价指标。灌溉定额是指进入到试验区域畦田内的灌水量之和。田间水利用系数是指根系层内实际灌入的水量与进入毛渠水量的比值。
采用式(19)与(20)分别计算试验区灌溉定额模拟值V及其与实测值间的相对误差RE

(20)
式中V为灌溉定额模拟值,m3;V为灌溉定额实测值,m3;V为模拟的任意畦田的灌水量,m3;为试验田总面积,m2;L为模拟的畦田长度,m;为模拟的田块数量。
采用式(21)与(22)分别计算基于实测值与模拟值的单个田块根系层的土壤平均含水率,
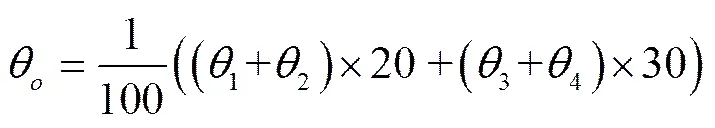
(22)
式中θ为基于实测值的根系层土壤平均质量含水率,%;θ为基于模拟值的计划湿润层土壤平均质量含水率,%;θ为模拟的0~100 cm范围内以1 cm为空间步长的各层土壤质量含水率,%;1、2、3、4为实测的各层土壤质量含水率,%。土壤根系层设为100 cm。
采用式(23)与(24)分别计算基于实测值或模拟值的田间水利用系数及两者间的相对误差RE:
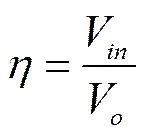
(24)
式中V为灌溉后试验区土壤根系层增加的总水量,m3;η为基于实测值计算的田间水利用系数;η为基于模拟值计算的田间水利用系数。
3.3 模型验证
基于上述模型参数,畦长方向和土壤垂向的空间离散步长分别取值2.0和0.01 m、土壤与地表水流时间离散步长均取值1 s时,采用由畦灌地表水流-土壤水动力学耦合模型于Monte-Carlo抽样建立的区域畦灌模拟方法,对3次试验方案下区域畦灌过程进行模拟。对3次典型区域畦灌实例而言,基于确定性模拟方法FIM的灌水效率分别为68.78%、65.23%、67.17%,灌水均匀度分别为63.45%、62.14%、63.87%,基于所建随机模拟方法SRM的灌水效率均值(标准差)分别为66.84%(8.45%)、67.23%(10.63%)、67.59%(9.21%)和63.23%(7.89%),灌水均匀度分别为61.58%(8.69%)、62.72%(8.36%)。可以看出,FIM与SRM之间的灌水效率和灌水均匀度之间存在一定的差异,而SRM通过标准差等指标可以有效描述区域畦田灌水质量的内在变异情况,FIM仅能采用固定指标值描述区域灌水质量。
表4给出了不同模拟方法下灌溉定额模拟值与实测值之间的相对误差与田间水利用系数模拟值与实测值间的相对误差。可以看出,SRM的灌溉定额最小相对误差为9.95%,最大相对误差为12.23%,而已有模拟方法FIM的灌溉定额最小相对误差为14.15%,最大相对误差为16.78%。这表明构建的模型具备优良的模拟区域畦灌过程的能力。2类模拟方法的灌溉定额模拟值与实测值间的误差,源于对土壤特性、畦田规格和地表糙率等灌溉参数区域空间变异性的捕捉精度有所差异。
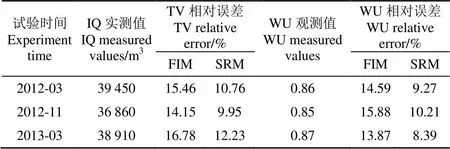
表4 基于模拟与实测的灌溉定额及田间水利用系数相对误差
注:FIM为确定性灌溉模型;SRM为随机参数灌溉模型。
Note: FIM is deterministic parameter irrigation model, SRM is stochastic parameter irrigation model.
SRM模拟情况下3个实例的田间水利用系数相对误差范围为8.39%~10.21%,而FIM的田间水利用系数相对误差范围为13.87%~15.88%。这表明考虑畦灌参数空间变异性的畦灌随机模拟方法能够更好地评估区域畦田灌水质量。2类模拟方法的模拟值与实测值间的误差,可能是因为模拟时将田块土壤特性空间变异性平均化处理,导致土壤水力特性参数值被过高或过低估计,或将田面微地形标准差及糙率系数概化处理,导致田面微地形和糙率系与实际情况有所偏差,从而影响对田间水利用系数的精确计算。
图3给出了灌溉后畦田根系层的土壤含水率模拟(SRM)与实测均值在空间上的累积概率分布情况。可以看出,虽然实测田块土壤平均含水率累积速度迟滞于模拟的土壤平均含水率累积速度,但模拟值与实测值的概率分布趋势具有良好的一致性。土壤平均含水率模拟值与实测值累计概率曲线间存在的误差,可能是因为模拟时对畦田微地形状况、田面糙率系数、土壤水力特性空间变异、入渗维数及作物吸水等因素概化所导致的。
基于区域农田耕作措施和种植作物相同,将量化田面微地形状况的田面相对高程标准差视为一致,并将作物生长状况等因素不以田块尺度加以区分,视当次模拟试验的田面糙率系数作为常数,但实际上各个田块的田面相对高程标准差存在差异,田面糙率系数因为作物长势客观存在的差异及田面相对高程空间分布的差异而存在不同。土壤水力特性空间变异性在单个田块及区域尺度上客观存在,但模型模拟时,这种空间变异性采用离散后分配给各个虚拟田块的方式加以表达,未能精确反映实际上单个田块土壤水力特性空间变异性对地表水流推进过程及入渗过程的影响。另外,数值模拟时畦灌地表水流推进过程可视为从畦首到畦尾的一维地表水流运动过程,且单个田块内土壤入渗参数在点尺度上处处相等,但实际畦灌时地表水流运动间或存在着沿畦宽方向的曲线或漩涡运动过程,导致地表水流推进锋不能同时到达相同畦田长度处。而作物根系通过影响土壤结构和直接吸收水分2种形式改变土壤水分运移路径,但模拟灌溉过程时忽略作物短期内的吸水过程。因此,模拟与实测土壤平均含水率累积概率分布之间的误差,是必然存在的。这种误差只能在建立模拟方法时,通过合理简化区域畦灌过程,建立精确合理的水流运动方程加以降低,在数值模拟时,通过输入切合区域畦灌实际环境的参数值加以缩小,但由于灌溉过程及参数的概化,并不能完全消除。
通过对灌水效率、灌水均匀度、灌溉定额、灌后土壤平均含水率累积概率分布及田间水利用系数的模拟与实测值间的对比分析,发现所建的区域畦灌数值模拟方法具有精确的模拟能力,但由于对土壤特性、田面糙率系数、畦田微地形状况、土壤入渗维数问题及作物吸水过程的概化,模型模拟结果与实测结果之间存在一定的误差。这需要在下一步研究中加以改进和完善。
4 结 论
采用Monte-Carlo抽样将具有空间变异性的区域灌溉参数离散表征为若干灌溉参数样本,分别输入给畦灌地表水流-土壤水动力学耦合模型,以模拟区域畦灌过程、评价区域畦田灌水质量。该模拟方法有助于降低区域畦灌参数空间变异性的精确捕捉受到人为因素干扰的程度。基于3次区域畦灌试验的实测数据和2个对比的区域畦灌数值模拟方法,验证了上述所建模拟方法的模拟效果。结果表明,区域畦田长度、入畦单宽流量、土壤砂粒、粉粒、黏粒、土壤容重、土壤有机质含量均服从正态分布。确定性模拟方法与所建方法模拟的灌水效率和灌水均匀度具一定差异。与对比的模拟方法相比,所建模拟方法的模拟值与实测值间的灌溉定额和田间水利用系数相对误差均较小,分别为9.95%~12.23%和8.39%~10.21%,而对比的确定性模拟方法下的模拟值与实测值间的灌溉定额和田间水利用系数相对误差则分别为14.15%~16.78%和13.87%~15.88%,畦田土壤平均含水率累积趋势表现出良好的一致性。所建模拟方法有效缩小了区域灌溉参数空间变异性未能很好描述所带来的模拟误差范围较大等问题,为区域畦田灌溉过程及灌水质量的精确评估、区域畦田灌溉优化设计和管理提供了技术指导。但由于所建模拟方法对土壤特性、田面糙率系数、畦田微地形状况、土壤入渗维数问题及作物吸水过程的概化,模拟与实测值之间存在一定的误差,这需要在下一步研究工作中加以改进和完善。
[1] Furman A. Modeling coupled surface-subsurface flow processes: A review[J]. Soil Science Society of America, 2008, 7(2): 741-756.
[2] Abbasi F, Feyen J, Roth R L, et al. Water flow and solute transport in furrow-irrigated fields[J]. Irrigation Science, 2003, 22(2): 57-65.
[3] Abbasi F, Šimůnek J, van Genuchten M Th, et al. Overland water flow and solute transport: Model development and field-data analysis[J]. Journal of Irrigation and Drainage Engineering, 2003, 129(2): 71-81.
[4] Zerihun D, Furman A, Warrick A W. Coupled surface-subsurface flow model for improved basin irrigation management[J]. Journal of Irrigation and Drainage Engineering, 2005, 131(2): 111-128.
[5] Bautista E, Zerihun D, Clemmens A J. Iterative coupling strategy for surface-subsurface flow calculations in surface irrigation[J]. Journal of Irrigation and Drainage Engineering, 2010, 136(10): 692-703.
[6] Banti M, Zissis Th, Anastasiadou-Partheniou E. Furrow irrigation advance simulation using a surface-subsurface Intera- ction model[J]. Journal of Irrigation and Drainage Engineering, 2011, 137(5): 304-314.
[7] 董勤各,许迪,章少辉,等. 一维畦灌地表水流-土壤水动力学耦合模型Ⅰ:建模[J]. 水利学报,2013,44(5):570-577.
Dong Qin’ge, Xu Di, Zhang Shaohui, et al. Coupled surface-subsurface hydrodynamic model for border irrigationⅠ: Model development[J]. Journal of Hydraulic Engineering, 2013, 44(5): 570-577. (in Chinese with English abstract)
[8] 董勤各,许迪,章少辉,等. 一维畦灌地表水流-土壤水动力学耦合模型II:验证[J]. 水利学报,2013,44(6):726-733.
Dong Qin’ge, Xu Di, Zhang Shaohui, et al. Coupled surface-subsurface hydrodynamic model for border irrigation Ⅱ. Validation [J]. Journal of Hydraulic Engineering, 2013, 44(6): 726-733. (in Chinese with English abstract)
[9] 章少辉,许迪,李益农. 基于混合数值解法的二维畦灌地表水流运动模拟I:模型建立[J]. 水利学报,2011,42(2):180-186.
Zhang Shaohui, Xu Di, Li Yinong. A 2D surface water flow simulation of basin irrigation based on a hybrid numerical method I. Establishment of model[J]. Journal of Hydraulic Engineering, 2011, 42(2): 180-186. (in Chinese with English abstract)
[10] Playan E, Slatni A, Castillo R, et al. A case study for irrigation modernization: II Scenario analysis[J]. Agricultural Water Management, 2000(42): 335-354.
[11] Paydar Z, Gallant J. A catchment framework for 1-D models introducing FLUSH and its application[J]. Hydrol Process, 2008, 22(13): 2094-2104.
[12] Awan U K, Tischbein B, Martius C. Combining hydrological modeling and GIS approaches to determine the spatial distribution of groundwater recharge in an arid irrigation scheme[J]. Irrigation Science, 2013, 31(4): 793-806.
[13] Skonard C J. A Field-scale Furrow Irrigation Model[D]. Nebraska: University of Nebraska, 2002.
[14] Minasny B, Mcbratney A. A conditioned Latin hypercube method for sampling in the presence of ancillary information[J].Computers & Geosciences, 2006, 32(9): 1378-1388.
[15] Rad M R P, Toomanian N, Khormali F, et al. Updating soil survey maps using random forest and conditioned Latin hypercube sampling in the loess derived soils of northern Iran[J]. Geoderma,2014, 232/234(12): 97-106.
[16] Shields M D, Zhang Jiaxin. The generalization of Latin hypercube sampling[J]. Reliability Engineering and System Safety, 2016, 148(12): 96-108.
[17] Goda T, Sato K. History matching with iterative Latin hypercube samplings and parameterization of reservoir heterogeneity[J]. Journal of Petroleum Science and Engineering, 2014, 114(2): 61-73.
[18] 章少辉,许迪,李益农. 基于混合数值解法的一维全水动力学模型[J]. 农业工程学报,2009,25(9):7-14.
Zhang Shaohui, Xu Di, Li Yinong. One-dimensional complete hydrodynamic model for border irrigation based on hybrid numerical method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(9): 7-14. (in Chinese with English abstract)
[19] García-Navarro P, Playán E, Zapata N. Solute transport modeling in overland flow applied to fertigation[J]. Journal of Irrigation and Drainage Engineering, 2000, 126(1): 33-40.
[20] Strelkoff T S, Clemmens A J, Bautista E. Field properties in surface irrigation management and design[J]. Hournal of Irrigation and Drainage Engineering, 2009, 135(5): 525-536.
[21] Mulder V L, de Bruin S, Schaepman M E. Representing major soil variability at regional scale by constrained Latin Hypercubeampling of remote sensing data[J]. Journal of Petroleum Science and Engineering, 2013, 21(1): 301-310.
[22] Bai Meijian, Xu Di, Li Yinong, et al. Stochastic modeling of basins microtopography: Analysis of spatialvariability and model testing[J]. Irrigation Science, 2010, 28(2): 157-172.
[23] 盛骤,谢式千. 概率论与数理统计[M]. 北京:高等教育出版社,1993.
[24] Schaap M G, Leij F J, van Genuchten M T. ROSETTA: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions[J]. Journal of Hydrology, 2001, 251(3/4): 163-176.
[25] Saxton K E, Rawls W J. Soil water characteristic estimates by texture and organic matter for hydrologic solutions[J]. Soil Science Society of America Journal, 2006, 70(5): 1569-1578.
[26] 白美健,李益农,涂淑芳,等. 畦灌关口时间优化改善灌水质量分析[J]. 农业工程学报,2016,32(2):105-110.
Bai Meijian, Li Yinong, Tu Shufang, et al. Analysis on cutoff time optimization of border irrigation to improve irrigated water quality[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(2): 105-110. (in Chinese with English abstract)
[27] 白美健,许迪,李益农. 微地形分布差异对畦灌过程及性能的影响模拟[J]. 农业工程学报,2008,24(11):1-6.
Bai Meijian, Xu Di, Li Yinong. Simulating effects of microtopography distribution difference on basin irrigation process and performances[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2008, 24(11): 1-6. (in Chinese with English abstract)
[28] 鲍士旦. 土壤农化分析[M]. 北京:中国农业出版社,1999.
[29] Lilliefors H W. On the Kolmogorov-Smirnov test for normality with mean and variance unknown[J]. Journal of the American Statistical Association, 1967, 62(318): 399-402.
[30] Bautista E, Clemmens A J, Strelkoff T S, et al. Modern analysis of surface irrigation systems with WinSRFR[J]. Agricultural Water Management, 2009a, 96(7): 1146-1154.
[31] Bautista E, Clemmens A J, Strelkoff T S, et al. Analysis of surface irrigation systems with WinSRFR: Example application[J]. Agricultural Water Management, 2009b, 96(7): 1162-1169.
Simulation and validation for regional border irrigation considering spatial variability of irrigation parameters
Dong Qin’ge1,2, Xu Di3※, Zhang Shaohui3, Bai Meijian3, Li Yinong3
(1.,712100,; 2.712100; 3.100038,)
The performance evaluation of regional scale border irrigation plays an important role in the improvement of surface irrigation management level, but the existing models present the shortcomings such as less accurately capturing the spatial variability of regional scale irrigation parameters. So the exiting models cannot be effectively applied to analyze the performance of regional scale border irrigation system. To solve this problem, the border surface-subsurface flow model was applied to describe the surface and subsurface water flow. The conservative complete hydrodynamic equation and the Richards equation were applied to describe the surface water flow and subsurface water flow in border irrigation, respectively. The finite-volume approach was applied to spatially discretize these governing equations to obtain good mass conservation ability. The Picard iteration approach was introduced to obtain the linearization of this nonlinear algebraic system. The mass conservation component of surface flow model and subsurface flow model were iteratively coupled at the same time step to obtain the convergence value of surface flow depth, and then the momentum conservation component of surface flow model was externally coupled based on the convergence value of both the surface flow depth and infiltration rate to update the surface flow velocity. Solutions were numerically computed using an improved hybrid numerical method for surface flow model and a proposed numerical solution method with high-order accuracy for subsurface flow model. Monte-Carlo sampling method was used to accurately capture the spatial variability of regional scale irrigation parameters and generate a large number of border irrigation parameters samples, which were input to border surface-subsurface model, respectively. Consequently, the border surface-subsurface water flow processes of regional scale could be accurately simulated.Three times border irrigation experiments at regional scale were performed to validate the proposed model in Mawan Irrigation District, located in Dongying City, Shandong Province. Soil samples were collected at 4 depths from the top, middle, and bottom of the border field to analyze soil bulk density, soil particle size distribution, and soil moisture. The soil hydraulic parameters were transformed from the abovementioned soil properties using the Rosetta model. The relative elevation values of the border bottom were observed using a water level gauge. The surface flow depth was measured using water depth measuring devices, which were placed at every observation point before the irrigation was initiated. The surface flow depth was used to estimate Manning’s roughness coefficient. And unit discharge, border length, and border width were observed in March 2012, November 2012, and March 2013. The validation results showed that the proposed model could well simulate regional scale border irrigation processes, and presented very good modeling accuracy. Specifically, the relative errors between the measured and simulated values by the proposed stochastic parameter irrigation model were 9.95%-12.23% and 8.39%-10.21% for irrigation quota and field water utilization coefficient, respectively. By contrast, the relative errors of irrigation quota and field water utilization coefficient based on the existing deterministic parameter irrigation models were 14.15%-16.78% and 13.87%-15.88%, respectively. Additionally, the cumulative probability distribution trends of average soil moisture after irrigation between the measured and simulated values present the satisfactory performance. Thus, the proposed model overcomes the shortcomings of existing models and provides a useful numerical analysis tool for the management and design of regional scale border irrigation system.
irrigation; Monte-Carlo method; soils; parameters; spatial variability; irrigation performance; numerical simulation
10.11975/j.issn.1002-6819.2017.09.001
S275.3; O212.2
A
1002-6819(2017)-09-0001-09
2016-07-22
2017-03-10
国家自然科学基金项目(51609237);中科院“西部之光”项目(XAB2015B04);国家863计划项目(2013AA102904);中央高校基本科研业务费专项资金项目(2452016104)
董勤各,男,河南南阳人,助理研究员,博士,主要从事畦沟灌节水技术、土壤水盐运移模拟研究。杨凌 西北农林科技大学水土保持研究所,712100。Email:qgdong2011@163.com
许迪,男,北京人,教授级高工,博士,主要从事灌溉技术理论与方法研究。北京 中国水利水电科学研究院,100038。 Email:xudi@iwhr.com
董勤各,许 迪,章少辉,白美健,李益农. 考虑灌溉参数空间变异的区域畦灌模拟与验证[J]. 农业工程学报,2017,33(9):1-9. doi:10.11975/j.issn.1002-6819.2017.09.001 http://www.tcsae.org
Dong Qin’ge, Xu Di, Zhang Shaohui, Bai Meijian, Li Yinong. Simulation and validation for regional border irrigation considering spatial variability of irrigation parameters[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(9): 1-9. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2017.09.001 http://www.tcsae.org

