雨强和糙度对坡面薄层流水动力学特性的影响

王俊杰，张宽地，杨 苗，范 典，龚家国



雨强和糙度对坡面薄层流水动力学特性的影响

王俊杰，张宽地※，杨 苗，范 典，龚家国

（1. 陕西省土地工程建设集团有限责任公司黄河西岸土地整治分公司，西安 710000； 2. 西北农林科技大学水利与建筑工程学院，杨凌 712100； 3. 西北农林科技大学黄土高原土壤侵蚀与旱地农业国家重点实验室，杨凌 712100； 4. 中国水利科学研究院流域水循环模拟与调控国家重点实验室，北京 100038）

基于流体力学和水力学基本理论，通过6个糙度、5个流量和5种雨强组合条件下的放水冲刷和模拟降雨试验，研究雨强和糙度对坡面流水动力学特性的影响。结果表明：在坡面薄层水流中，床面糙度对坡面流阻力有“增阻”效应，但在粗糙尺度为1.77 mm时产生拐点；降雨条件下，坡面流自由表面失稳的动态演化过程显著，其波动临界条件为黏深比0.382 4、0.599 3，在整个动态过程中阻力系数都随着降雨强度增加而减小；结合黏滞阻力、雨强阻力构建层流过渡区阻力计算公式，决定系数为0.92（<0.05），可以较好地为坡面流模型的建立提供参考依据。研究成果有助于从泥沙运动力学的角度揭示坡面流层流失稳的本质，为坡面流理论的发展奠定基础。

降雨；水动力学；糙度测定；雨强；坡面流；滚波

0 引 言

坡面流是由降雨或融雪在扣除地面填洼、截留以及下渗等损失后在重力作用下沿着坡面运动的浅层明流，它是坡面侵蚀的初始动力，同时也是造成土壤及母质破坏、搬运、沉积的关键因素[1-2]。坡面流一般水深只有几个毫米，沿程流向不稳定，且不断有质量源、动量源汇入[2-4]，并且易受下垫面条件、降雨强度、地表覆盖度[5-7]和试验坡度等条件影响，使得其相关研究更加复杂，有待进一步深入探讨。

目前，坡面流的研究主要集中在流态分析和阻力分析方面。关于坡面流流态方面， Horton[8]将坡面流流态定义为介于层流和紊流之间的混合流态；Emmett[9]通过试验分析将坡面流定义为不同于层流、过渡流和紊流的“扰动流”；吴淑芳等[10]通过野外放水冲刷试验将水流流态定义为与流量和下垫面相关的一种流态；沙际德等[11]通过理论推导与试验相结合的方法将坡面流流态定义为介于层流和紊流之间的过渡流；张光辉[12]通过变坡水槽试验将水流流态定义为与水深密切相关的过渡流与紊流；张宽地等[13]通过加糙床面的放水试验定义流态指数，提出“层流失稳”的概念。在坡面流阻力方面，其影响要素主要集中在下垫面条件与雨强2个方面。施明新等[14-15]通过模拟糙度的定床冲刷试验，认为阻力随糙度（糙度是反应下垫面粗糙情况的常用指标）增加而增大；而蒋昌波等[16]认为颗粒阻力与形态阻力最本质的区别在于粗糙单元如何与水相互作用，在糙度不断增大的过程中，2种阻力形式会发生转变，故不应单纯认为阻力系数随糙度的增加而增大。又如：陈国祥等[17]通过模拟降雨试验表明降雨具有增加坡面流阻力的作用；张宽地等[18-20]通过相关领域不同方面的试验研究认为阻力系数跟雨强成反比例关系；而潘成忠等[21]通过研究表明雨强对阻力系数无影响；但是，张小娜等[22]通过室内模拟试验得出了阻力系数随着雨强增大呈现先增加后减小的趋势，结论与前者的存在差异。由此可见，对坡面流的研究成果虽然已经有诸多问世，但是存疑颇多，而且只有极少数研究[23]涉及滚波，对滚波的影响有待进一步研究。

本文通过模拟降雨同放水冲刷相结合的方法，对不同雨强、糙度条件下坡面薄层水流的水动力学特性做系统性的研究，阐明雨强、糙度对坡面流水动力特性的影响，并给出考虑雨强、糙度作用的坡面流阻力计算公式，旨在促进坡面薄层流理论的发展。此外，本研究将有助于从泥沙运动学的角度探究坡面层流失稳的本质，为构建坡面流侵蚀模型奠定理论基础。

1 材料与方法

1.1 试验设计与方法

本模拟降雨试验在中科院水利部水土保持研究所的人工降雨大厅中进行，采用QYJY-503固定式人工模拟降雨系统，该系统主要分为4大部分：供水系统、降雨系统、控制系统、显示系统。该降雨大厅分为4个相互独立的降雨区，降雨高度均为16 m，降雨均匀度大于0.80，雨滴大小的调控范围是0.4～5 mm，雨强的连续变化范围是30～300 mm/h。

综合坡面薄层水流自身的复杂性和测量数据的准确性2方面因素，确定了如下几项试验设计要点：

1）本试验采用可调坡度的钢架水槽，并在底部铺设3 cm厚的硅酸盐玻璃，以此保证槽底的水平。坡度调节采用单个油压升降立柱并配合双刚性支架来实现，试验所用钢槽长6.00 m、宽0.50 m、深0.25 m，试验坡度为15.0°。

2）为保证落在钢槽底板上的雨滴动量相近，还原自然降雨条件下坡面流的情况，本试验降雨高度均控制在16 m。考虑黄土高原临界侵蚀雨强为30.0～36.0 mm/h，而最大峰值雨强为144.0 mm/h[24]，本试验雨强共设置5个梯度：0、60.0、90.0、120.0、150.0 mm/h。每场模拟降雨开始前，都需要通过雨量筒对雨强进行率定，调整为设计雨强。

3）考虑到黄土高原地区多年平均降水量（550 mm）及最大暴雨强度（144.0 mm/h[24]），并结合预试验获得的坡面流失稳的可能单宽流量范围0.210～0.952 L/(min·m)，钢槽上游放水单宽流量确定为0.176、0.331、0.481、0.658、0.991 L/(min·m)，共5个处理。考虑到光面条件下坡面流特殊水力现象（即光面条件下，坡面流失稳流量变化范围太大）的研究，去掉雨强150.0 mm/h，同时单宽流量增加了3个处理，分别为1.322、1.655、2.488 L/(min·m)。钢槽的尾部设置有漏斗形的集水装置，每个流量工况开始前，都需通过体积法测流量3次，取其平均值作为本试验流量。

4）为模拟天然下垫面的糙度，试验共计6种模拟糙度，包括硅酸盐玻璃光面（糙度近似为0），另外5种是通过粘贴水纱布与砂子结合的方法来实现，粘贴的水纱布分别为240、120、240目，按照国标换算后的粒径分别为0.061、0.12、0.70 mm，粘贴的砂子换算后的粒径分别为1.77、3.68 mm。本文采用了尼库拉兹在20世纪30年代提出的床面糙度表示方法，糙度尺寸用粗糙度系数k表示，其值代表粘贴砂砾的平均直径[13]。

5）沿钢槽设纵向设置5个观测断面，即以溢流板为原点向槽身下端0.5、1.5、2.5、3.5、4.5 m共设计5个观测断面。其中，每个观测断面的横向均选取-15、0、+15 cm（相对于水槽纵轴）3个测点，采用潍坊金水华禹生产的SLZ60型水位测针（精度0.1 mm）测量水深，取3次测量值的平均值，然后减去本试验工况中粘贴砂粒直径的1/2，所得结果为该工况的断面平均水深。

6）本试验采用4个可调式流量供水器来实现供水流量，4个流量供水器的流量调节范围分别为0～12、5～15、5～20、10～40 L/min。当流量较小的时候用第1个可调式流量供水器，其余的情况的都是通过这4个供水器的排列组合提供。在钢槽的来流端配置了1套试验稳流装置，包括稳流箱、溢流板、稳流栅、稳流板4个部分。通过这4部分的配合，可以将水流平顺的过渡到槽面，消除进口扰动，减小试验误差。

1.2 水力参数计算

断面平均流速。平均流速是坡面薄层水动力学要素中一个非常重要的指标，是衡量水流强度的主要指标。依据水力学中水流连续性方程，断面垂线平均流速可采用实测断面平均水深来求解，其计算公式[24]为

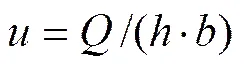
式中为断面平均流速，m/s；为试验流量，m3/s；为实测断面平均水深，m；为水槽宽度，m，本实验取0.5 m。

水流雷诺数。水力学二元流雷诺数[18]可表示为

式中为水力半径，m，采用水深近似代替；ν为水流运动黏性系数，cm²/s，采用泊谡叶公式计算

（3）

式中为水温，℃。

Darcy-Weisbach阻力系数[24]为：

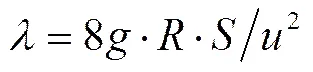
式中为水力坡度，近似取水槽坡度；为重力加速度，取9.81 m/s2。

摩阻流速[18]为：

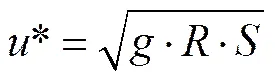
式中为摩阻流速，m/s。

黏性底层厚度[18]为：

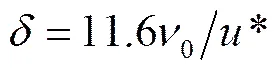
式中为黏性底层厚度，m。

绕流雷诺数R[11]为：

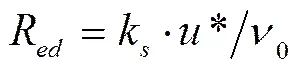
式中k为粗糙度系数，m。

水流佛汝德数。明渠水流理论[24]计算公式为

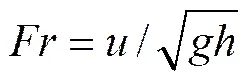
临界水深h

（9）

式中为综合修正系数，它与流速的分布密切相关，流速分布越均匀综合修正系数越大，通常h的取值范围1.4~1.6，考虑坡面流流速分布均匀的特点，这里将坡面流简化为宽浅水流[11]，取综合修正系数1.5，则临界水深的计算公式

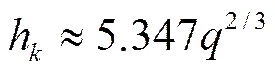
式中h为临界水深，mm；为单宽流量，L/(s·m)。

2 结果与分析

2.1 粗糙度和雨强对阻力的影响

对于人工加糙条件下坡面流水动力特性的研究已屡见不鲜[23-25]，而糙度对坡面薄层水流阻力特性的影响，目前没有明确的定论。为了更加明晰糙度对坡面流阻力特性的影响，将本试验的数据同敬向锋等[7]、张宽地等[2]的部分试验数据点绘于图1。文献[2,7]的试验数据均是在无降雨条件下，坡度为15.0°时，采用粘贴砂粒及水纱布加糙的方法获得的。

由图1可以看出，当糙度k≤1.77 mm时，随着糙度的不断增加，坡面流阻力系数的数据点离层流线=96/[24]和紊流线=0.316 4/0.25[24]的距离愈来愈远，即阻力系数愈来愈大；当k>1.77 mm时，随着糙度的增加，阻力系数随着雷诺数的增加呈现震荡稳定趋势。究其原因，从坡面薄层水流的阻力分割的角度分析，坡面流阻力是由颗粒阻力、形态阻力、波阻力、降雨阻力组成，阻力的最终表现是这4种阻力相互耦合、影响的结果。考虑到本组试验是在定床、无降雨条件下完成的，故暂且不考虑波阻力和雨强阻力的影响。当糙度k≤1.77 mm时，水流漫过颗粒的最上端，阻力形式以颗粒阻力为主，随着粒径的增大，绝对糙度增大，阻力系数变大；当糙度k>1.77 mm时，水流绕过颗粒运动，颗粒阻力与形态阻力此消彼长，随着粒径的增大，绕流阻力基本保持相对稳定。此外，水流漫过颗粒产生的是横轴涡旋，横轴涡旋的向上扩散会产生竖向脉动，横轴涡旋受颗粒大小的影响比较大；而水流绕过大颗粒将会产生竖轴涡旋，水流内部结构会变得更加紊乱，受颗粒大小的影响不太显著。

雨强对坡面薄层水流的增阻与减阻问题，一直颇受争议。梅欣佩[26]曾通过水槽试验和土槽试验相对比的方法，表明试验下垫面条件对坡面流的影响既可能是增阻作用也可能是减阻作用。为了更进一步研究雨强和垫面情况对坡面流阻力的影响，故将光面试验条件和人工加糙条件的试验数据点绘在如图2所示的双对数坐标系中。

a.k≈0

b.k=0.061 mm

图2 雨强对薄层水流增阻的影响

Fig.2 Influence of rainfall intensity on water added resistance of thin layer

由图2分析可知，光面上，阻力系数都随着雨强增大而减小，即降雨强度对坡面流具有“减阻”效应，同时糙度越大（k=0～1.77 mm）时，阻力系数的数据点距离层流线、紊流线的距离越远，数据点越集中。其中的原因可能要归为雨滴动量分量的影响，坡度一定时，沿坡面方向的分量与垂直坡面的分量一定。雨强越大，水流获得动量越大，速度越大，阻力系数越小。小糙度（k=0.061 mm）相对于光面（k≈0）时坡面流阻力是增大的（图1），此时雨滴动量沿坡面方向分量对流速的增量减小，故阻力系数的变化不大，数据点较为集中。

2.2 黏性底层的影响

在明渠相关理论中，黏性底层被定义为紧靠流动边界并且未受到或很少受到到紊动作用影响的一种极薄的层流层。黏性底层受到水流雷诺数的影响很大，受流速和水深的综合影响较为显著。同时，坡面薄层水流以其水深小、流速复杂而成为研究界的热点，并且也因此区别于明渠水流。为了进一步地研究坡面薄层水流的相关性质，将黏性底层厚度同平均水深的数据点绘在图3。

试验现象中可以发现，无论雨强和糙度如何变化，坡面薄层流中总有水流以滚雪球的形式沿着坡面向下运动，将其称为滚波流。目前对于滚波流的研究多集中在理论分析[27]，很少涉及试验研究[28]。滚波流作为一种波流耦合流，既具有孤波波动的性质，同时又结合着冲击波的特点。当雨强和糙度较小时，坡面流就会以滚波的形式运行，随着糙度和雨强的逐渐增大，达到一定的临界水力条件，滚波逐渐消失。然而，继续改变糙度和雨强，达到另一个新的临界水力条件时，这种波动的滚波流会重现，此时的滚波形态较前者会有一定的变化。

图3给出了各种工况下，滚波流形态转变临界条件关系图。滚波流是坡面流中惯性力同黏滞力相互作用的又一个新的平衡状态，这种状态是通过牺牲局部流体质点来达到水流整体的光滑运动。本试验中的水力临界条件沿用了黏深比/这一参数，由于k=3.68 mm下滚波失稳现象更明显，转捩临界点更易判断，具有代表性，故采用糙度k=3.68 mm时滚波产生、消失、再产生时黏深比（0.599 3和0.382 4）作为临界黏深比。当/<0.382 4时，此时坡面流进入了滚波区（层流失稳区），水流以滚波的形式下泄；当0.599 30.599 3时，坡面流进入滚波I区。由图3还可以看出，两临界点间/的差值约0.24，这可能与滚波演化规律有关。由于本文试验条件的限制，后续的研究将会对此做更近一步的探讨。

2.3 贴壁绕流

绕流雷诺数与雷诺数为作为流态判别的依据，绕流雷诺数用于泥沙运动中，而雷诺数则大都用在明渠流中。在泥沙运动学中，绕流雷诺数下临界值取值范围是0.2～0.5，这里取为0.35；上临界值的取值范围是800～1 000，这里取为900[7]。考虑到本试验是人工贴沙的条件下进行的，采用泥沙运动学理论，更为客观，故用绕流雷诺数更加合理。因此，将阻力系数与扰流雷诺数点绘在如图4所示的双对数坐标系中。由图4可以看出，在相同糙度、雨强条件下，Darcy-Weisbach阻力系数随绕流雷诺数R的增加而减小；相同糙度条件下，阻力系数随着雨强增大而减小，并且不同雨强的趋势线相距很近，甚至会相交；不同糙度条件下，随着糙度的增大阻力系数的变化区间分别为1.25～2.6、1.3～2.7、1.8～3.0、1.8～3.15、1.8～3.15，总体上表现出先增大后稳定的现象。

由坡面薄层水流的相关研究可知，坡面薄层流阻力中颗粒阻力起主要作用时，阻力系数会随着雷诺数的增加而减小，以形态阻力为主时，阻力系数随着雷诺数的增加而增大。在本试验中由于黏砂粒径较小，颗粒阻力占主导作用，故阻力系数会随绕流雷诺数的增加呈现幂函数减小的趋势[24]。在相同糙度条件下，雨强对坡面具有“减阻”效应，同时考虑到可能由于雨强间隔较小，阻力系数随雨强的增大而减小，同时两条或不同雨强趋势线会很接近，甚至相交。阻力系数和绕流雷诺数之所以会随着糙度的增加而增大，是因为坡面薄层水流水深浅，床面状况对水流的内部结构（尤其是流速分布）影响剧烈，进而影响水流流态、阻力状况。而最终能达到稳定状态，可能与横轴涡旋向竖轴涡旋的转变有关，竖轴涡旋条件下水流更加紊乱，阻力系数趋于稳定，同时绕流雷诺数增大。

由图4进一步分析可知，本试验绕流雷诺数的取值范围是0.35～36.1，参照绕流雷诺数过渡流范围0.35～900[7]，本试验研究中的所有工况均处于过渡流的状态。然而，若按照传统明渠雷诺数的判别标准，本试验将处于过渡流与层流都有的状态。可见判别标准依然需要进一步的研究探讨，和更多的理论来支持。

2.4 临界水深

在明渠相关理论中，流型的判别方法共有4种：弗汝德数判别法、微波流速法、临界水深判别法、临界底坡判别法。根据流型的判别标准，当>1时，明渠流处于急流状态，当<1时，明渠流处于缓流状态，当=1时，明渠流处于临界流状态。不同流型时比动能的差距很大，因此，流型的判别在坡面流侵蚀机理的研究中发挥着重要作用。

坡面薄层水流时常会受到表面张力、流速分布结构等因素的影响，因此，明渠弗汝德数判别法和微波流速法在坡面流流型判别领域中尚存在缺陷。考虑到急缓流还可以通过临界水深h来进行判别，且临界水深受断面形状影响大，受表面张力、流速结构因素影响较小，故这里采用h作为流型判别的标准。当>h时，坡面流处于缓流区；当<h时，坡面流处于急流区；当=h时，坡面流处于临界流。

为了更清晰地描述坡面薄层流的流型，让急流区、缓流区更加直观的表现出来，将试验数据点绘在图5中。由图5分析可知，坡面薄层水流在本试验条件下，大部分均处在急流区，只有少部分处于缓流区。同时，随着糙度增加，坡面流会从急流区向缓流区转捩。

本试验的试验坡度设定在15°，比梁志权等[29]认为的临界坡度10°（即=0.173 6）大因而坡面流大部分处于急流状态。考虑到随着坡面糙度逐渐增大，水流的阻力逐渐增加，在宏观上的表现就是水位雍高，水深增加。当水深逐渐增加，超过临界水深时，水流从急流区转捩到缓流区。

2.5 阻力系数的通式

关于坡面流阻力的计算公式，已有不少前辈做了相关的研究，并取得了一定的成果。例如：沙际德等[11]曾根据理论推导给出了坡面流阻力系数的计算通式，张宽地等[18]又通过模拟降雨试验给出了沙黄土坡面流阻力计算公式。但两者都是在没有考虑雨强作用的影响下给出的计算公式。在自然界中的坡面流侵蚀过程往往伴随着降雨，可见雨强对坡面流阻力的影响是不可忽视的，应该进一步的讨论和研究。

根据阻力分割的思想，坡面薄层水流的阻力分为黏滞阻力、绕流阻力、降雨阻力[30]、波阻力[31]4部分。本试验采用模拟定床加糙试验，试验中床面形态不发生变化，不考虑波阻力的影响。因此，综合考虑黏滞阻力、绕流阻力以及降雨阻力的计算形式，并结合本试验的试验特点，运用多元回归分析的方法，将降雨条件下坡面阻力的计算通式总结如式（11）。

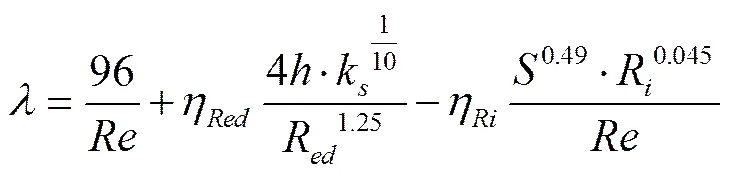
式中η为绕流阻力修正系数，采用雨强为0、90、150 mm/h时的试验数据进行多元回归分析，多元回归结果η为182.24；k为粗糙度系数，mm；η为雨强阻力修正系数；R为雨强，mm/h。

由式（11）和（12）可以看出，η为正值，式（11）的第三项为负值，对于阻力系数而言，雨强增大，公式（11）第3项越小，阻力系数值减小，这也就验证了前面降雨对坡面具有减阻作用的结论。为了探讨式（11）的合理性，将雨强为60、120 mm/h时的阻力系数计算值与阻力系数实测值绘制在直角坐标系中，如图6。

由图6可以看出，阻力系数的计算值与实测值都在1:1线附近，2=0.92（<0.01），但也有个别试验点偏离直线较远，这可能是由于相同雨强下不同糙度的相互影响作用，同时试验测量过程滚波现象的产生在一定程度上影响着测量的精度。可见，要想更加细致地研究坡面的相关性质，有必要在测量手段以及测量精度方面下更多的功夫。

3 讨 论

本文通过模拟降雨与人工加糙相结合的方法，同时研究了雨强、下垫面糙度对坡面流阻力特性的影响，意在揭示雨强、糙度作用下坡面流“增阻”现象的本质。

通过将本试验数据同敬向锋等[7]结合分析后发现，坡面流阻力会随着糙度的增大逐渐增大，当到达临界值后，糙度的增加反而会使坡面流阻力减小。坡面流的“增阻”产生的条件也有待进一步研究。同时文章给出了不同雨强条件下坡面薄层水流阻力规律，意在揭示降雨对坡面薄层水流的“减阻”效应。在文章的后面又给出了阻力计算新公式，相对于沙际德的阻力公式，该公式加入了绕流阻力的作用，相对于张宽地等[18]，该公式又加入了雨强阻力的因素。该阻力计算新公式更加符合实际，计入公式的因素更多，对于坡面流阻力计算会产生一定的积极作用。

坡面流水深较小，受雨强、下垫面条件影响剧烈。虽然本文给出了雨强、定床加糙下垫面对坡面流阻力特性的影响，但对于坡面流失稳机理的探讨以及失稳规律的研究，尚显不足。另外，对于下垫面条件的研究也仅限于定床加糙，这里忽略了植被分布、形态等因素的影响。本文仅在坡度为15°的条件下进行研究。若要更进一步的说明降雨的减阻作用，应该从多坡度的角度考虑。本文的研究仅是对坡面薄层水流阻力规律的初步探索，对于今后更进一步的研究，仍需要进行更深层次的试验。

4 结 论

本文通过6个糙度、5个流量和5种雨强组合条件下的放水冲刷和模拟降雨试验，系统研究了雨强和糙度对坡面流水动力学特性的影响，结果表明：

1）从泥沙运动力学与紊流力学的角度来看，坡面薄层水流下垫面糙度的尺寸效应，影响着横轴涡旋与纵轴涡旋的比例，进而影响坡面流增阻的一致性，产生增阻变化的拐点。

2）降雨条件下，坡面薄层水流坡面形态处于自由表面失稳而又不断发育的波动状态，其临界值用黏深比表示为0.3824、0.5993，在整个过程中阻力系数随着降雨强度的增加而减小。

3）本试验将泥沙运动力学的绕流雷诺数、绕流阻力引入到坡面薄层流理论中，与传统雷诺数结果相比，采用绕流雷诺数分析的流区分布更贴切试验现象。本文将绕流阻力、降雨阻力引入阻力计算，给出降雨条件下层流过渡区的阻力计算公式，通过本文实测资料与理论计算值的对比，其2=0.92（<0.05）。

[1] 施明新，吴发启，田国成. 地表糙率对坡面流流速影响的试验研究[J]. 水力发电学报，2015，34(6)：117－123.

Shi Mingxin, Wu Faqi, Tian Guocheng. Experimental study on effect of surface roughness on overland flow velocity[J]. Journal of Hydroelectric Engineering, 2015, 34(6): 117－123. (in Chinese with English abstract)

[2] 张宽地，王光谦，孙晓敏，等. 坡面薄层水流水动力学特性试验[J]. 农业工程学报，2014，30(15)：182－189.

Zhang Kuandi, Wang Guangqian, Sun Xiaomin, et al. Experiment on hydraulic characteristics of shallow open channel flow on slope [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(15): 182－189. (in Chinese with English abstract)

[3] Dunkerley D. Flow threads in surface runoff: Implications for the assessment of flow properties and friction coefficients in soil erosion and hydraulics investigations [J]. Earth Surface Processes and Landforms, 2004, 29(8): 1012－1026.

[4] Ali M, Sterk G, Seeger M. Effect of flow discharge and median grain size on mean flow velocity under overland flow[J]. Journal of Hydrology, 2012, 337(453): 150－160.

[5] 肖培青，姚文艺，申震洲，等. 草被减流减沙效应及其力学机制分析[J]. 中国水土保持科学，2010，8(2)：15－19.

Xiao Peiqing, Yao Wenyi, Shen Zhenzhou, et al. Reduction effects of grass on runoff and sediment and its mechanical mechanism[J]. Science of Soil and Water Conservation, 2010, 8(2): 15－19. (in Chinese with English abstract)

[6] 杨帆，张宽地，马小玲，等. 植被覆盖度对坡面流相对水

动力学特性的影响[J]. 水力发电学报，2017，36(2)：29－39.

Yang Fan, Zhang Kuandi, Ma Xiaoling, et al. Effect of vegetation coverage on relative hydrodynamics of overland flows[J]. Journal of Hydroelectric Engineering, 2017, 36(2): 29－39. (in Chinese with English abstract)

[7] 敬向锋，吕宏兴，潘成忠，等. 坡面薄层水流流态判定方法的初步探讨[J]. 农业工程学报，2007，23(5)：56－61.

Jing Xiangfeng, Lü Hongxing, Pan Chengzhong, et al. Preliminary study on flow pattern determinant method of shallow flow on slope surface[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2007, 23(5): 56－61. (in Chinese with English abstract)

[8] Horton R E. Erosional development of streams and their drainage basins: Hydrophysical approach to quantitative morphology[J]. Geological Society of America Bulletin, 1945, 56: 275－370.

[9] Emmett W W. Overland flow [M]//Kirkby M J. Hillslope Hydrology. New York: John Wiley & Sons, 1978: 145－176.

[10] 吴淑芳，吴普特，原立峰. 坡面径流调控薄层水流水力学特性试验[J]. 农业工程学报，2010，26(3)：14－19.

Wu Shufang, Wu Pute, Yuan Lifeng. Hydraulic characteristics of sheet flow with slope runoff regulation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(3): 14－19. (in Chinese with English abstract)

[11] 沙际德，蒋允静. 试论初生态侵蚀性坡面薄层水流的基本动力特性[J]. 水土保持学报，1995，9(4)：29－35.

Sha Jide, Jiang Yunjing. Attempt for expounding basic dynamic characteristics of very shallow flow on preliminary eco-erosion slopes[J]. Journal of Soil and Water Conservation, 1995, 9(4): 29－35. (in Chinese with English abstract)

[12] 张光辉. 坡面薄层流水动力学特性的实验研究[J]. 水科学进展，2002，13(2)：159－165.

Zhang Guanghui. Study on hydraulic properties of shallow flow[J]. Advances in Water Science, 2002, 13(2): 159－165. (in Chinese with English abstract)

[13] 张宽地，王光谦，王占礼，等. 人工加糙床面薄层滚波流水力特性试验[J]. 农业工程学报，2011，27(4)：28－34.

Zhang Kuandi, Wang Guangqian, Wang Zhanli, et al. Experiments on hydraulic characteristics of roll wave for sheet flow with artificial rough bed[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2011, 27(4): 28－34. (in Chinese with English abstract)

[14] 施明新，吴发启，田国成，等. 地表粗糙度对坡面流水动力学参数的影响[J]. 灌溉排水学报，2015，34(7)：83－87. Shi Mingxin, Wu Faqi, Tian Guocheng, et al. Influence of surface roughness on hydrodynamic parameters of overland flow[J]. Journal of Irrigation and Drainage, 2015, 34(7): 83－87. (in Chinese with English abstract)

[15] 翟艳宾，吴发启，张一，等. 人工模拟粗糙度对坡面流阻力的影响[J]. 灌溉排水学报，2014，33(1)：93－95. Zhai Yanbin, Wu Faqi, Zhang Yi, et al. Impact of simulated surface roughness on resistance coefficient of overland flow[J]. Journal of Irrigation and Drainage, 2014, 33(1): 93－95. (in Chinese with English abstract)

[16] 蒋昌波，隆院男，胡世雄，等. 坡面流阻力研究进展[J]. 水利学报，2012，43(2)：189－196. Jiang Changbo, Long Yuannan, Hu Shixiong, et al. Recent progress in studies of overland flow resistance[J]. Journal of Hydraulic Engineering, 2012, 43(2): 189－196. (in Chinese with English abstract)

[17] 陈国祥，姚文艺. 降雨对浅层水流阻力的影响[J]. 水科学进展，1996，7(1)：42－46.

Chen Guoxiang, Yao Wenyi. Effect of rainfall on hydraulic resistance of shallow flow[J]. Advances in Water Science, 1996, 7(1): 42－46. (in Chinese with English abstract)

[18] 张宽地，王光谦，吕宏兴，等. 模拟降雨条件下坡面水流水动力学特性试验研究[J]. 水科学进展，2012，23(2)：229－235.

Zhang Kuandi, Wang Guangqian, Lü Hongxing, et al. Experimental study of shallow flow hydraulics on a hillslope under artificial rainfall conditions[J]. Advances in Water Science, 2012, 23(2): 229－235. (in Chinese with English abstract)

[19] 肖培青，郑粉莉，姚文艺. 坡沟系统坡面径流流态及水力学参数特征研究[J]. 水科学进展，2009，20(2)：236－240.

Xiao Peiqing, Zheng Fenli, Yao Wenyi. Flow pattern and hydraulic parameter characteristics in hillslope-gully slope system[J]. Advances in Water Science, 2009, 20(2): 236－240. (in Chinese with English abstract)

[20] 刘刚，郑世清，田风霞，等. 坡度与降雨强度对植物路路面侵蚀动力参数的影响[J]. 水土保持学报，2009，23(4)：44－49.

Liu Gang, Zheng Shiqing, Tian Fengxia, et al. Influence of slope and rainfall intensity on runoff and erosion hydraulic characteristics on grassed roadways[J]. Journal of Soil and Water Conservation, 2009, 23(4): 44－49. (in Chinese with English abstract)

[21] 潘成忠，上官周平. 降雨和坡度对坡面流水动力学参数的影响[J]. 应用基础与工程科学学报，2009，17(6)：843－851.

Pan Chengzhong, Shangguan Zhouping. Experimental study on influence of rainfall and slope gradient on overland shallow flow hydraulics[J]. Journal of Basic Science and Engineering, 2009, 17(6): 843－851. (in Chinese with English abstract)

[22] 张小娜，冯杰，张超，等. 不同雨强下土壤大孔隙对坡面流水动力学参数的影响[J]. 河海大学学报，2012，40(3)：264－269.

Zhang Xiaona, Feng Jie, Zhang Chao, et al. Influence of soil macropore on hydrodynamic parameters of overland flow with different rainfall intensities[J]. Journal of Hohai University, 2012, 40(3): 264－269. (in Chinese with English abstract)

[23] 杨苗，张宽地，龚家国，等. 坡面薄层水流滚波演变规律试验研究[J]. 农业机械学报，2016，47(10)：156－163.

Yang Miao, Zhang Kuandi, Gong Jiaguo, et al. Experiment on evolution law of thin layer rolling flow on slope surface[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(10): 156－163. (in Chinese with English abstract)

[24] 张宽地，王光谦，吕宏兴，等. 坡面浅层明流流态界定方法之商榷[J]. 实验流体力学，2011，25(4)：67－73.

Zhang Kuandi, Wang Guangqian, Lü Hongxing, et al. Discussion on flow pattern determination method of shallow flow on slope surface[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(4): 67－73. (in Chinese with English abstract)

[25] 赵春红，高建恩，王飞，等. 阻力形式对坡面流流速修正系数的影响[J]. 农业机械学报，2013，44( 10)：130-135.

Zhao Chunhong, Gao Jian'en, Wang Fei, et al. Effects of resistance forms on velocity correction factor of overland flow [J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(10): 130-135. (in Chinese with English abstract)

[26] 梅欣佩. 降雨条件下坡面薄层水流水动力学特性试验研究[D]. 西安：西安理工大学，2004.

Mei Xinpei. Experimental Study on Hydrodynamic Characteristics of Sheet Flow on Slope under Rain[D]. Xi’an: Xi’an University of Technology, 2004. (in Chinese with English abstract)

[27] Richard G L, Gavrilyuk S L. A new model of roll waves: Comparison with Brock’s experiments[J]. Journal of Fluid Mechanics, 2012, 698: 374－405.

[28] Zanuttigh B, Lamberti A. Roll waves simulations using shallow water equations and weighted average flux method[J]. Journal of Hydraulic Research, 2002, 40(5): 610－622.

[29] 梁志权，卓慕宁，郭太龙，等. 不同雨强及坡度下坡面流的水动力特性[J]. 生态环境学报，2015，24(4)：638－642.

Liang Zhiquan, Zhuo Muning, Guo Tailong, et al. Effects of rainfall intensity and slope gradient on hydrodynamic characterics of overland flow[J]. Ecology and Environmental Science, 2015, 24(4): 638－642. (in Chinese with English abstract)

[30] Savat J. The hydraulics of sheet flow on a smooth surface and the effect of simulated rainfall[J]. Earth Surface Processes and Landforms, 1977(2): 125－140.

[31] Abrahams A D, Parsons A J, Hirsch P J. Field and laboratory studies of resistance to inter rill overland flow on semiarid hillslopes, Southern Arizona[C]//Overland Flow: Hydraulics and Erosion Mechanics. London: UCL, 1992: 1－24.

Influence of rainfall and roughness on hydrodynamic characteristics of overland flow

Wang Junjie, Zhang Kuandi※, Yang Miao, Fan Dian, Gong Jiaguo

(1.,710000; 2.,,712100,; 3.,,712100,; 4.,,100038,)

Overland flow is the initial motivation of slope surface erosion and the key reason for soil degradation. In order to study the influence of rainfall intensity and roughness on slope surface water dynamic characteristic, the artificial simulated rainfall experiments were carried in the Soil and Water Conservation Engineering Laboratory in Northwest A&F University. Based on the basic theory of fluid mechanics and hydraulics, the influence of rainfall intensity and roughness on hydrodynamic characteristics of overland flow was meticulously investigated. The experiment included 6 roughness, 5 flow discharges and 5 rainfall intensity. The theory of friction velocity and viscous sublayer in sediment movement mechanics were also applied in this study. Results showed that under the stage of overland flow, the data points of flow resistance coefficient was far from the laminar flow line and turbulent flow line with the continuous increase of roughness when the roughness was smaller than or equaled to 1.77 mm, indicating that the bed surface roughness of slope surface had an effect of resistance increase to flow resistance. However, the resistance coefficient fluctuated to being relative stable when the roughness was greater than 1.77 mm. Under the rainfall condition, the resistance coefficient decreased with the increase of rainfall intensity when roughness was closer to 0. In addition, the resistance coefficient was concentrated when the roughness increased. Under the stage of different rainfall intensity and roughness, the overland flow was accompanied by production and disappearance of roll wave. The phenomenon could be expressed by the ratio of viscous sublayer thickness and mean water depth. By observation, the ratio at roughness of 3.68 mm when the roll wave was obvious was calculated. When the ratio was between 0.382 4 and 0.599 3 (the difference was 0.24), the overland flow was in transition zone, otherwise, in roll wave zones. On the conditions of same roughness and rainfall intensity, Darcy-Weisbach resistance coefficient would decrease with the increase of turbulent flow Reynolds number. Under the condition of the same roughness, the resistance coefficient decreased with the increase of rainfall intensity. The resistance coefficient was 1.25-2.6, 1.3-2.7, 1.8-3.0, 1.8-3.15, 1.8-3.15, showing a trend of increase than being stable with increase of resistance coefficient. The turbulent flow Reynolds number was 0.35-36.1, belonging to transitional flow zone (0.35-900) according to turbulent flow Reynolds number standard but belonging to transitional and laminar flow zone according to traditional Reynolds number standard. It indicated that the standard for overland flow deserved further study. Based on the critical water depth, the overland flow was in rapid zone mostly. As the roughness increased, the flow transferred from rapid zone to slack zone. In addition, this study provided an overland flow resistance calculation formula by comprehensively considering viscous resistance, circle resistance and rainfall resistance. By validation, the formula had a high accuracy with2of 0.92 (<0.05). The results are helpful to understand hydraulic flow erosion mechanism of slope surface, and provide data support for building soil erosion model.

precipitation; hydrodynamics; roughness measurement; rainfall intensity; overland flow; roll wave

10.11975/j.issn.1002-6819.2017.09.019

S157.1

A

1002-6819(2017)-09-0147-08

2016-04-29

2016-10-10

国家自然科学基金项目（51579214、51209222、41001159）；国家973计划课题（2015CB452701）；流域水循环模拟与调控国家重点实验室开放基金（IWHR-SKL-2014）；黄土高原土壤侵蚀与旱地农业国家重点实验室主任基金（A314021402-1619）

王俊杰，男，新疆博乐人，主要从事工程水力学及坡面流侵蚀研究。咸阳市西北农林科技大学水利与建筑工程学院，712100。 Email：wangjunjie091@163.com

张宽地，男，宁夏隆德人，副教授，博士，主要从事水工水力学及坡面水流研究。咸阳市西北农林科技大学水利与建筑工程学院，712100。Email：zhangkuandi428@163.com

王俊杰，张宽地，杨 苗，范 典，龚家国. 雨强和糙度对坡面薄层流水动力学特性的影响[J]. 农业工程学报，2017，33(9)：147－154. doi：10.11975/j.issn.1002-6819.2017.09.019 http://www.tcsae.org

Wang Junjie, Zhang Kuandi, Yang Miao, Fan Dian, Gong Jiaguo. Influence of rainfall and roughness on hydrodynamic characteristics of overland flow[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(9): 147－154. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.09.019 http://www.tcsae.org