基于DEM-FEM的AZ31B板材软模成形极限预测
曹秒艳,李建超,苑亚宁,赵长财,董国疆
基于DEM-FEM的AZ31B板材软模成形极限预测
曹秒艳1,李建超2,苑亚宁2,赵长财2,董国疆3
(1. 燕山大学国家冷轧板带装备及工艺工程技术研究中心,秦皇岛 066004;2. 燕山大学先进锻压成形技术与科学教育部重点实验室(燕山大学),秦皇岛 066004;3. 燕山大学车辆与能源学院,秦皇岛 066004)
针对金属板材固体颗粒介质成形工艺中散体颗粒的离散性能和板材连续变形特点,提出并构建离散元−有限元耦合仿真模型。通过试验和数值模拟相结合的方法,建立镁合金板材温热成形韧性破裂准则,并验证该准则的有效性。最后结合韧性断裂准则对AZ31B镁合金固体颗粒介质筒形件温热拉深进行离散元−有限元耦合模拟,对其成形极限进行预测分析,并展开相应条件下的拉深成形试验。结果表明:基于韧性断裂准则的离散元−有限元耦合分析方法可以有效预测镁合金板固体颗粒介质温热拉深成形极限。
离散元;有限元;镁合金;固体颗粒介质;成形极限
镁合金具有密度低、比强度高、弹性模量大、减震性好、承受冲击能力强、耐有机物和碱的腐蚀性能良好等特点,成为航空器、航天器和火箭导弹等制造工业中最有前途、最轻的金属结构材料[1−2]。由于密排六方结构,镁合金在室温下塑性变形能力较差,经常出现断裂破坏并阻碍了板材的进一步成形。如何提高镁合金的塑性成形能力以适应结构件的使用要求并且准确预测工件内部和表面裂纹发生的时间和位置对镁合金板材塑性成形过程的工艺制定和模具设计具有重要的意义[3]。
成形极限的理论预测是利用屈服准则和塑性本构关系,通过板料拉伸成形过程中发生颈缩与断裂进而计算得到成形极限的方法[4],目前预测材料成形极限的方法有4种,即成形极限图(FLD)、应力成形极限图(FLSD),最大减薄率和韧性断裂准则。成形极限图能够定量地评价不同加载路径下的成形极限,其应用较广,但该法基于比例加载条件下建立,对于试样的非平面变形区域以及非线性应变加载等情况,FLD准则均不适用,此外,获得材料FLD参数的实验也相对复杂[5]。成形极限应力图认为当拉力大于材料的极限应力时,材料便会发生断裂。由于材料的极限应力无法简单地直接测量得到,而且极限应力大小会随着应力状态的变化而改变。故用这种方法来预测成形极限存在很大的误差[6]。最大变薄率是板料断裂时的最大厚度变薄率。然而这种方法难以预测易脆断材料的断裂[7]。因此,不少学者提出多种应用韧性断裂准则预测板材成形极限,该方向已成为当前研究热点[8−12]。这些准则大多建立在宏观连续介质力学和热力学的基础上,通过引入损伤的概念来描述大变形过程中材料内部的微孔洞和微裂纹的发展演化。这种预测方法不因应变路径的改变而发生变化,且考虑成形过程中的应变速率、温度等参数,具有很强的适用性[12]。不过目前韧性断裂准则的研究尚处于起步阶段,并未出现一个大家公认的适用于所有成形条件下的统一规范。这些准则中应用比较广泛的是Cockcroft-Latham准 则[8]和OYANE等[9]提出的韧性破裂准则。Cockcroft- Latham准则认为,对于给定的材料,在一定的温度及应变速率下,导致材料破坏的主要因素是成形过程中的最大拉应力,即拉应力达到某一阈值时,材料发生破坏。Oyane准则考虑了静水应力作用,使得该准则不仅能够定量表示瞬时的损伤状况,更体现了加载过程中整个应力及应变历史对材料的劣化效应。TAKUDA等[10]将Oyane准则应用到板料的圆筒件拉伸和内孔翻边成形工艺分析来预测成形极限,并与试验结果对比,得到了很好的一致性。
固体颗粒介质成形(Solid granules medium forming,SGMF)工艺是采用固体颗粒代替刚性凸模(或凹模)的作用,对金属板材进行拉深、胀形的工艺,在提高金属管板材成形极限和零件表面质量,简化模具结构,尤其是复杂零件精密成形、难加工材料成形、温热成形等方面体现了独特的优势,目前已引起国内外关注和应用[13−15]。
当前,分析颗粒物质特性强有力工具是自20世纪70年代开始出现并发展起来的离散元法(Discrete element method, DEM),诸多学者运用这一工具对颗粒体系的多尺度结构展开了深入研究[16−17]。离散元法在揭示颗粒物质内部力链结构、颗粒相互接触变形及传力特性等细观特征方面具有其它方法无法比拟的优点;而有限元法(Finite element method, FEM)可以有效模拟金属板材在承受压力下的成形过程。为了充分利用上述两种分析方法的优点,提出颗粒介质和金属板材分别采用离散元和有限元分别计算,然后通过力与位移边界数据实时交互建立耦合平台对金属板材SGMF工艺进行模拟分析。DEM-FEM耦合分析已应用于分析轮胎和沙地接触作用问题[18]、岩石开凿[19]、三体摩擦界面中接触行为[20]等。但上述方法中采用有限元分析的对象仅限于弹性变形问题,对于SGMF工艺中颗粒散体与塑性变形体耦合变形过程的分析仍有待研究。
本文作者通过实验和数值模拟相结合的方法,建立镁合金板材温热成形韧性破裂准则,并基于该准则对镁合金板材固体颗粒介质热拉深成形进行DEM- FEM耦合仿真分析,对成形极限进行预测。通过实验验证预测结果的准确性,从而验证了该方法的适用性。
1 DEM-FEM耦合模型建立
固体颗粒介质DEM-FEM分体耦合仿真分析的思路是将连续成形过程离散化。应用离散元法分析颗粒介质传压规律,应用有限元法分析板材变形特征,并将分析结果与加载条件相互转换传输,运用颗粒介质加载和变形迭代运算的控制方式,实现DEM-FEM分体耦合仿真。本研究中采用DEM-FEM双向耦合方法,实现颗粒的运动与金属板材变形实时影响和相互作用,即在考虑了金属板材对颗粒运动影响的同时,也考虑了颗粒对金属板材变形量的影响。
1.1 离散元基本原理
本研究中颗粒介质主要为近似均匀的球形颗粒,因此,采用圆球单元作为研究对象,分析颗粒介质成形的颗粒传力特性。球体运动学模型[21]主要采用牛顿第二定律,在时步下,颗粒的线运动方程为
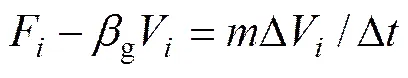
式中:=1,2,3,分别为、、坐标;F为不平衡力矩分量;V为线速度分量;为质量;g为整体阻尼系数。颗粒的转动方程如下:
(2)
式中:M为不平衡力矩分量;为旋转角速度分量;为转动惯量。求解式(1)和(2)可得各速度分量。然后确定增量线位移与增量角位移进而得到颗粒新的位置和。由各颗粒新位置坐标决定相邻颗粒是否接触或是原接触点是否脱离。相互接触的球会产生假性重叠量,再由接触模型公式分别求出接触力和,返归式(1)和(2)迭代。
其接触模型如图1所示。本研究中采用线性接触刚度模型,每个接触由法向和切向两个线性弹簧组成法向刚度因数n和切向刚度系数s。在切线方向存在以摩擦因数为m的滑动。颗粒之间允许重叠,其重叠量与弹簧刚度组合后即可计算接触力值。法向力和切向力可分别由以下两式给出:
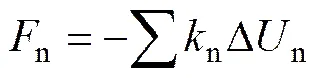
(4)
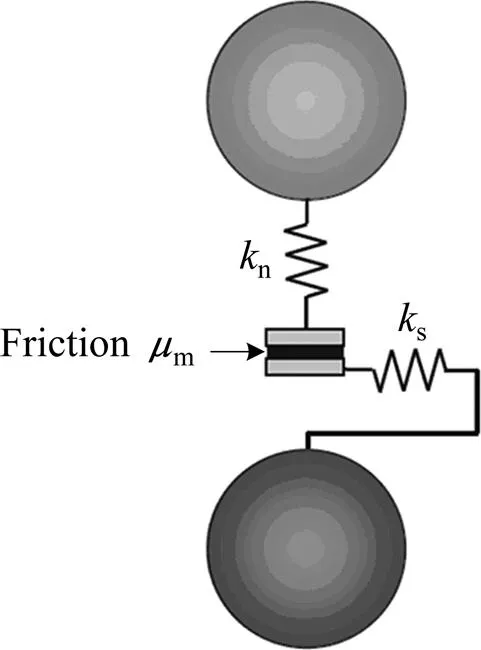
图1 离散元接触模型
1.2 板材颗粒介质成形DEM-FEM分体耦合原理
金属板材颗粒介质成形DEM-FEM分体耦合技术策略如图2所示。其研究方法如下:基于颗粒DEM模型得到介质与边界(板材)之间的接触压力,将该接触压力作为板材FEM模型的压力输入条件,进而得到新的板材变形几何形状;再将该几何形状作为颗粒DEM模型新的几何边界,同时加载新压力()进行迭代循环运算,直至目标产品成形;最后基于板材成形性能试验实测数据,建立误差评估和运算成本评估策略,对模型进行修正,最终建立合理的DEM-FEM分体耦合仿真模型。基于该仿真模型,对镁合金目标工件成形进行模拟分析。引入破裂准则,预测破裂产生的过程和特点,获得目标工件成形的最佳控制方法及工艺参数匹配策略。

图2 颗粒介质成形DEM-FEM分体耦合技术流程图
本研究中的颗粒介质由粒径为0.12~0.14 mm的球形颗粒组成。运用离散元软件PFC2D对颗粒介质进行研究。通过颗粒介质单轴压缩试验确定该介质法向刚度系数n、切向刚度系数s及颗粒间摩擦因数、颗粒与墙体摩擦因数等参数[22],具体模拟参数值见表1。
颗粒介质DEM分析中,压头采用单排球体颗粒簇组成,以伺服力的方式对颗粒介质施加预设压力,如图3所示。上侧位置插图为球体颗粒簇构成的压头通过力链的形式将压力传递至下方接触的颗粒介质,然后经颗粒介质将压力以接触力链的形式传递至板材内表面,见右侧插图,图中的数字为板材单元编号。

表1 颗粒介质DEM模拟参数

图3 颗粒介质DEM分析模型
从DEM分析中得到颗粒介质与其底部边界的接触压力,再将该接触压力调入至基于商用软件ABAQUS的板材FEM模型中,作为压力施载的边界条件,如图4所示。

图4 金属板材FEM分析模型
在金属板材颗粒介质成形DEM-FEM分体耦合技术策略中,颗粒介质与板材之间的接触压力和位移边界数据实时交互是其关键一环。从离散元软件中导出的数据结果包含了板材所有单元或节点的载荷信息,这些信息需作为载荷条件输入到有限元软件中;另外,有限元分析处理后板材变形所更新的单元位置坐标数据将作为离散元中板材墙体新的位置边界条件。为了有效完成上述过程中产生巨大数据量处理,利用Visual Basic语言编程开发,建立耦合仿真数据交互传输程序模块。
在金属板材颗粒介质成形工艺中,不论是室温成形还是温热成形,均可应用DEM-FEM分体耦合技术策略建立其成形仿真模型。由于镁合金室温塑性较差,因此,这里主要讨论温热条件下基于DEM-FEM镁合金板材成形极限预测。
2 镁合金板材成形韧性破裂准则
由于镁合金室温条件下塑性低,成形性能差,而提高其成形温度可以有效提高其成形性能,因此镁合金板材成形一般均在温热条件下进行。虽然诸多学者在预测板材成形极限时提出了多种韧性断裂准则,这些准则主要针对板材冷成形工艺,对适合考虑温度场的热力耦合问题的板材温热成形的韧性断裂准则的研究则较少。
2.1 镁合金温热成形韧性破裂准则的建立
为考虑温度及应变速率对镁合金变形力学性能的影响,苌群峰等[23]在Oyane损伤模型的基础上提出考虑温度效应的韧性破裂准则如下:

式中:为积分值;σ为静水应力,MPa;为变形温度,℃;为破裂时的等效应变;为应变速率,s−1;为等效应变。式(5)表示为、、的泛函。当=1时,即可判断破裂。在一定的变形温度和应变速率的条件下,关于、的函数和的取值可分别表示为材料参数、。则式(5)可表示为
(6)
2.2 镁合金温热成形韧性破裂准则中材料参数的确定方法
一般情况下,确定温热成形韧性破裂准则中的材料参数需要在不同温度和应变速率进行系列平面应力和平面应变试验,工作量巨大。故在本研究中采用试验结合有限元模拟的方法确定材料参数。其确定步骤如下:
1) 由单向拉伸实验得出的实际伸长率作为模拟中的位移边界条件;
5) 由基于SGMF工艺镁合金板材极限拉深试验得出数值模拟的位移边界条件;
7) 综合步骤4)和6)即可得到某一指定温度和应变速率下的材料参数。
按照上述方法,确定基于SGMF工艺的镁合金板材韧性破裂准则中的材料参数,详细过程如下。
2.2.1 通过单向拉伸实验及模拟获取材料参数关系
单向拉伸实验选用厚度为1.0 mm商用AZ31B镁合金板材。拉伸实验在InspektTable100电子万能试验机上进行。得到不同应变速率及温度条件下的真实应力应变曲线如图5所示。
2.2.2 通过极限拉深试验及模拟获取材料参数关系
基于SGMF工艺的AZ31B镁合金筒形件拉深成形示意图及试验装置如图7所示。由图7可知,成形试验时,板材放置于凹模上,压边圈对板材施加压边力;压头与板材之间充满固体颗粒介质。法兰及凹模环向均匀分布有若干加热棒对板材及颗粒介质进行加热,并设置有热电偶对板材温度进行监控,当温度达到指定值时,压头以速度匀速下行压缩固体颗粒介质迫使工件变形。本研究中凹模直径为80 mm,其圆角半径d8 mm。
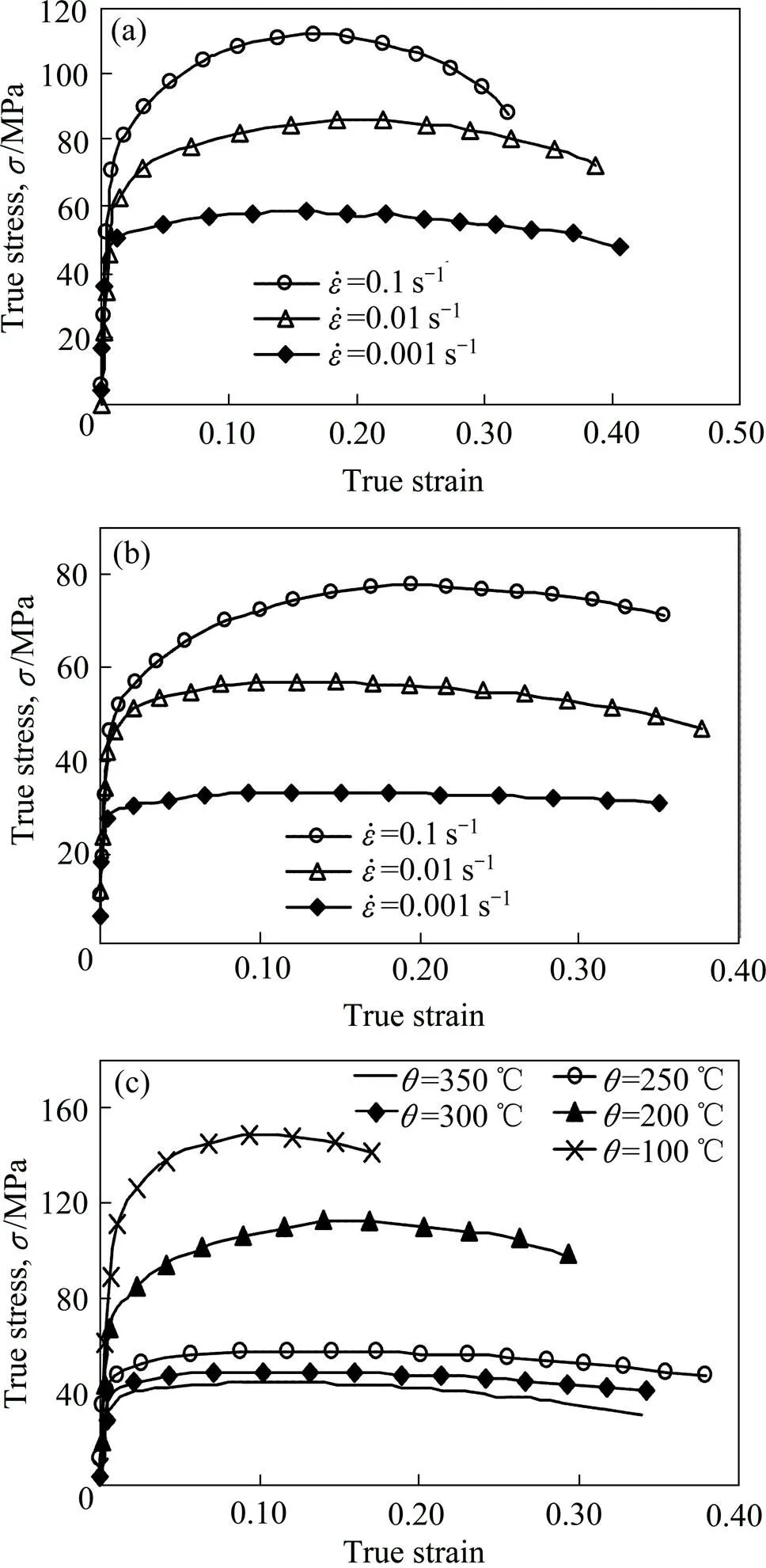
图5 AZ31B镁合金不同条件下的真实应力应变曲线
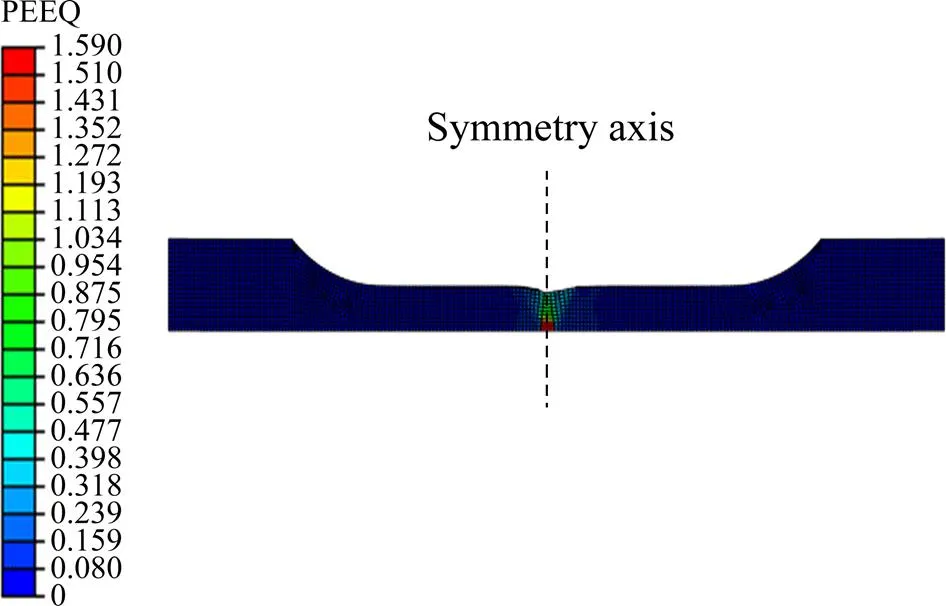
图6 试样单向拉伸断裂时等效应变云图

图7 镁合金板材颗粒介质拉深成形原理及试验装置图
为获得镁合金拉深极限,将工件压边力施加足够大,保证在拉深过程中法兰不变形。板材与介质加热至指定的温度后,压头下行实施工件拉胀成形,直至工件破裂。
厚度为1 mm,直径为150 mm的AZ31B镁合金板坯,在成形温度为200 ℃、应变速率0.1 s−1的条件下进行极限拉深试验。压头行程为23.8mm时工件破裂。将半径为0的原始坯料在径向上分成若干等份,标出测量点距离中心轴的初始位置,如图8所示,待工件成形后,根据这些测量点进行积分值的计算。
基于DEM-FEM耦合进行极限拉深模拟时,板材性能曲线采用单向拉伸实验测定的成形温度为200℃、应变速率0.1 s−1的真实应力应变曲线(见图5)。该拉深成形为等温成形,故不考虑温度场的影响。板材单元类型仍为S4R;由DEM分析得到的固体颗粒介质接触压力,按照相应的位置坐标点施加于板材单元上。由表1所列颗粒介质DEM模拟参数可知,DEM分析中已经考虑了板材边界与颗粒介质之间的摩擦,因此该接触压力为颗粒介质与板材之间法向力和切向摩擦力的合力。这种介质对板材主动摩擦力施加的特点正是SGMF工艺区别于充液成形等软模成形工艺的特点。板材与压边圈、板材与凹模之间摩擦条件设置为库伦摩擦,其摩擦因数为0.08。本数值模型中,除了板材与颗粒介质为变形体外,其余各部件均定义为刚体。参考极限拉深试验建立相应的数值模型,按照试验中的位移边界条件,得到压头位移为23.8mm时的工件等效应变云图如图9所示。选取破裂单元,获取该单元的主应力,通过计算得到静水应力,结合该单元的等效应变、等效应力,代入式(6),得到材料常数关系式
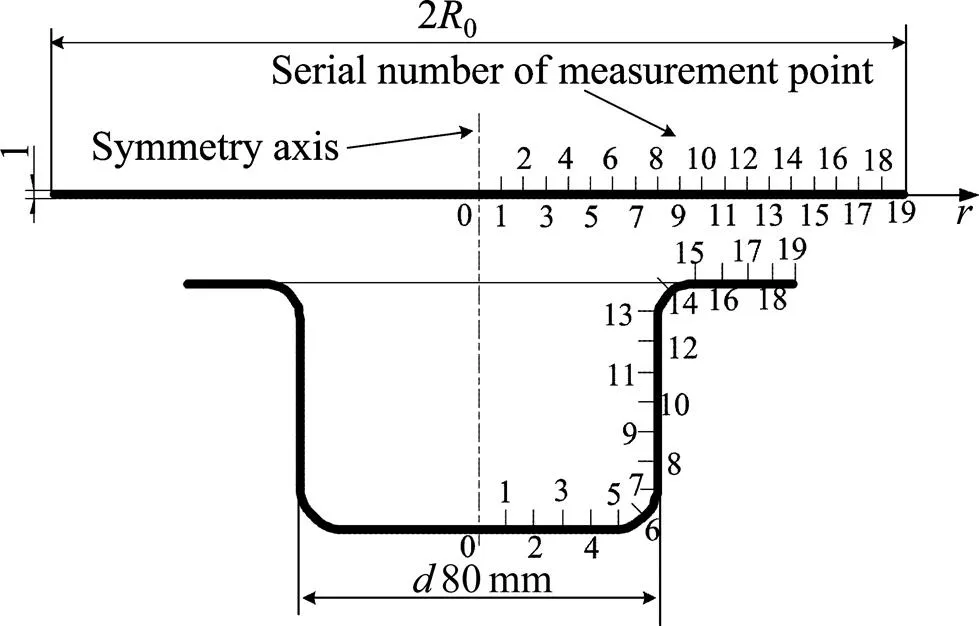
图8 镁合金板材拉深筒形件示意图

图9 AZ31B板材DEM-FEM耦合极限拉深等效应变云图
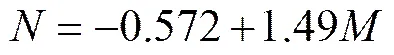
同理,按上述方法可求得不同温度,不同应变速率下的材料参数、的值。对于其余应变速率和温度的值则可以插值得到。由此,可得到不同温度和应变速率下,考虑温热效应的镁合金韧性破裂准则。
3 基于DEM-FEM的镁合金板颗粒介质成形极限预测
3.1 镁合金温热成形韧性破裂准则验证
为了验证考虑温度的镁合金韧性判断准则的有效性,分别将单向拉伸实验和颗粒介质极限拉深试验结果与根据韧性判断准则得出的结果进行比较。图10所示为温度200 ℃,应变速率0.1 s−1条件下单向拉伸位移为16.1 mm时的准则积分值分布图。从图10中可以看出:拉伸试件单元积分值自中轴线附近向夹持端逐渐降低,中轴线处的单元积分值为1.3,已经超过临界值1,出现破裂,这与试验拉伸试件首先在中间位置发生颈缩然后直至从中间断裂的结果是一致的。
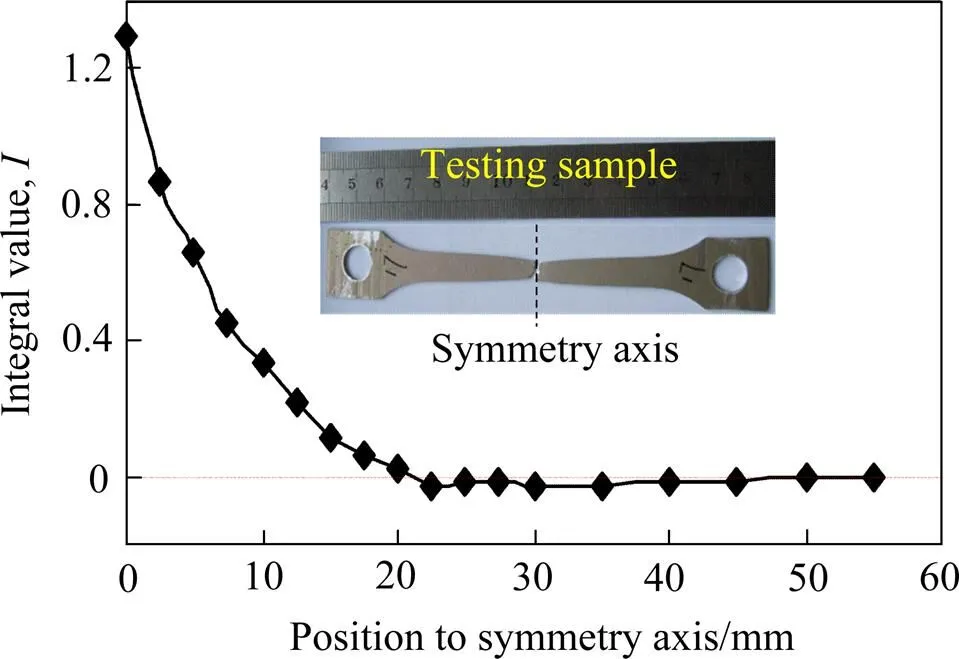
图10 AZ31B单向拉伸实验积分值I曲线
图11所示为基于DEM-FEM分体耦合模拟极限拉深,压头位移分别为17.5 mm、23.8 mm和25.2 mm时,根据韧性破裂准则得到的积分值沿拉深工件径向分布曲线。由图11可知,当压头位移为17.5 mm时,工件底部中心处积分值达到最高为0.522,整个底部值均在0.5以上,可见整个底部处于胀形状态;当压头行程为23.8 mm时(见图6),距离中心轴25 mm位置的单元=1,正好达到破裂状态,底部其余位置接近1;当压头位移达到25.2 mm时,底部所有单元积分值均超过1,并且仍以距离中心轴25 mm位置的单元积分值最高。从图11也可以看出,随着压头的下行,最危险区域由底部中心处逐渐向底部圆角处移动,并最终在该处破裂,该结果与极限拉深试验工件的实际情况相吻合,如图11中插图所示。由此可见,在考虑温热效应韧性破裂准则的基础上运用DEM-FEM耦合仿真对镁合金SGMF工艺成形极限的预测具有较好的可靠性。
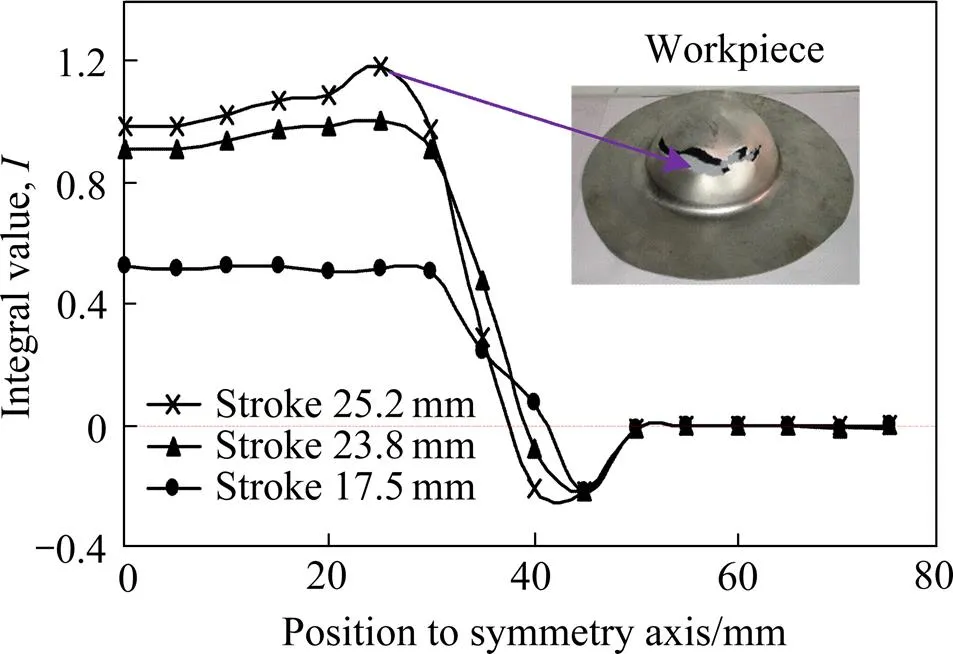
图11 镁合金板材极限拉深试验的积分值I曲线
3.2 镁合金板材颗粒介质温热成形极限预测
金属板材颗粒介质软模拉深成形有限元数值模拟中,一般采用将颗粒介质近似为连续体的处理方法,然后通过分析工件壁厚模拟值对板材拉深破裂做出定性判断。但由于无法充分考虑颗粒的离散特性,使得该方法在实现对破裂发生在某一位置单元和拉深高度进行定量判断时不甚准确。借助于考虑温度的镁合金韧性判断准则并运用DEM-FEM耦合技术为上述问题的解决提供了新的方法。
图12所示为板材厚度为1 mm,固定压边间隙为1.4 mm,成形温度为300 ℃,压头速度为2 mm/s时,板材不同拉深阶段时的断裂准则积分值变化曲线。结合图12对应的等效应变云图可以看出,拉深初始(压头位移为30 mm)时,底部区域为积分值相对较高部位,随着拉深的进行迅速过渡至与底部圆角相连的传力部位。由于自由变形时,底部形状为近似球冠形,因此,软凸模圆角处的高应变区(危险区)并不明显。板材各处积分值均小于0.3,处于安全状态;当工件筒形直壁形成后,该传力区成为了积分值的最高区域,并最终在该处出现破裂。当压头位移70 mm时,该处的积分值为1.45,说明该处已经破裂。产生破裂的原因在于压边间隙过大,法兰起皱严重,阻碍了板材向凹模内流动。进一步研究发现,当压头位移为66 mm时,该处积分值为1,即此时为临界状态。通过进行上述条件下的颗粒介质成形试验,得到其拉深试验工件,见图12插图,与积分值分析结果一致。由此可见,镁合金板材颗粒介质拉深成形中,直壁传力区为最容易破裂区,并且采用考虑温度的韧性破裂准则并运用DEM-FEM耦合仿真分析可以对该破裂失稳的具体位置和发生时刻进行准确判断。
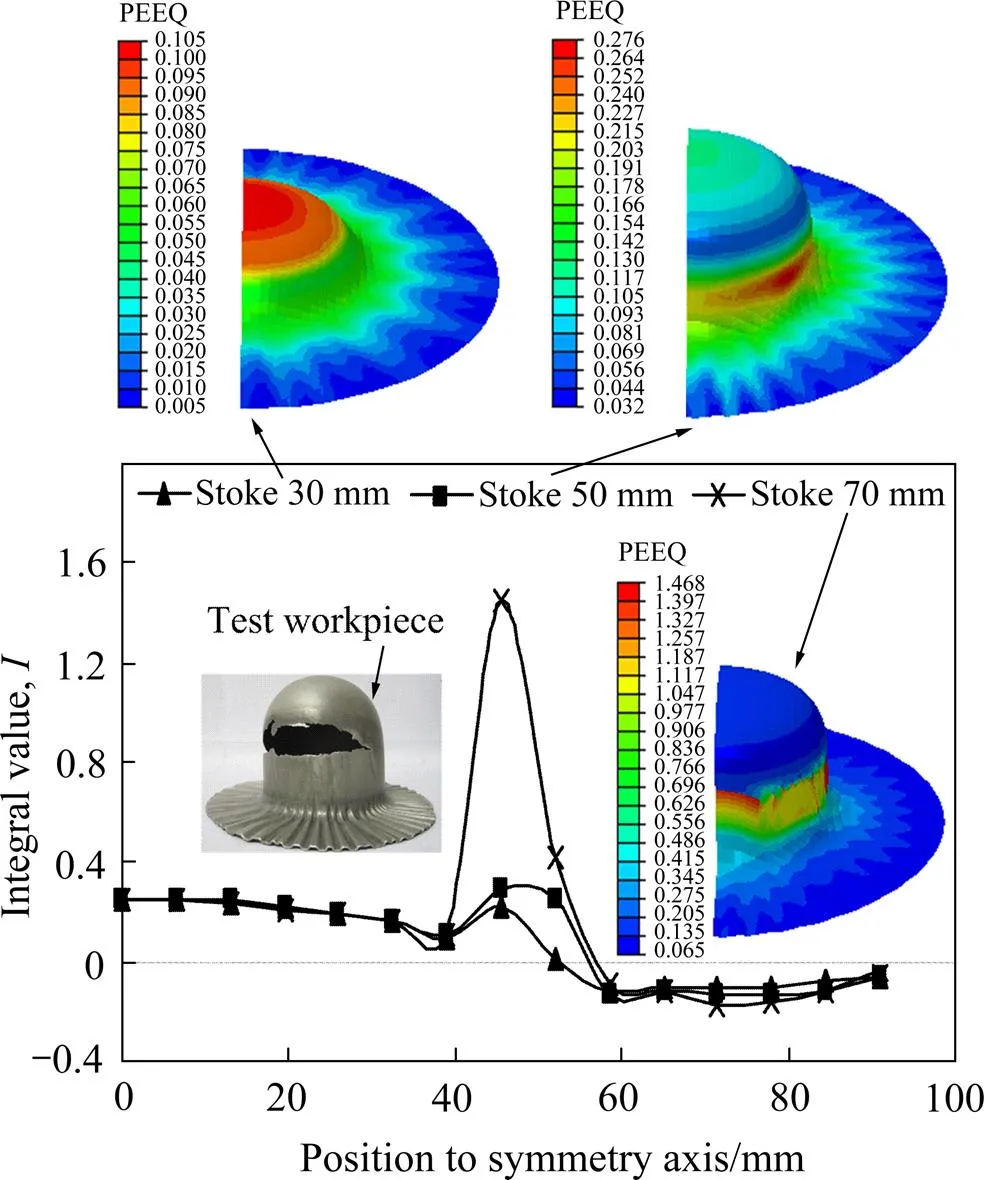
图12 不同拉深阶段的积分值曲线及等效应变云图
4 结论
1) 采用DEM-FEM分体耦合技术充分展示了SGMF工艺区别于其他软模成形工艺的特点。DEM分析可以体现颗粒介质离散特性,同时也考虑了颗粒介质对板材切向摩擦力的主动施加,FEM分析则体现了金属板材连续变形特点。
2) 采用DEM-FEM分体耦合数值模拟,并以考虑温度的韧性破裂准则作为考核板材破裂的依据,更能准确预测基于SGMF工艺的镁合金拉深成形极限。这可以为该软模拉深工艺开发提供依据,实现工艺参数的量化和优化设计。
3) 通过对镁合金板材颗粒介质温热拉深成形极限预测和成形试验的对比,验证了预测结果和试验的结果一致性,证明了运用韧性破裂准则并结合DEM-FEM分体耦合技术对镁合金板材颗粒介质温热拉深成形极限预测的准确性。
[1] 余 琨, 黎文献, 王日初, 马正青. 变形镁合金的研究、开发及应用[J]. 中国有色金属学报, 2003, 13(2): 277−288.YU Kun, LI Wen-xian, WANG Ri-chu, MA Zheng-qing. Research, development and application of wrought magnesium alloys[J]. The Chinese Journal of Nonferrous Metals, 2003, 13(2): 277−288.
[2] 宁俊生, 范亚夫, 彭秀峰.镁合金在大变形和高应变速率下塑性变形研究进展[J]. 材料工程, 2007(9): 67−73. NING Jun-sheng, FAN Ya-fu, PENG Xiu-feng. Research and progress of plastic deformation of magnesium alloys at high strain rate and large deformation[J]. Engineering of Material, 2007(9): 67−73.
[3] 陈振华, 刘俊伟, 陈 鼎, 严红革. 镁合金超塑性的变形机理、研究现状及发展趋势[J]. 中国有色金属学报, 2008, 18(2): 193−202.CHEN Zhen-hua, LIU Jun-wei, CHEN Ding, YAN Hong-ge. Deformation mechanisms, current status and development direction of superplastic magnesium alloys[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(2): 193−202.
[4] 马高山, 万 敏, 吴向东. 基于M-K模型的铝锂合金热态下成形极限预测[J]. 中国有色金属学报, 2008, 18(6): 980−984. MA Gao-shan, WAN Min, WU Xiang-dong. Theoretical prediction of FLDs for Al-Li alloy at elevated temperature based on M-K model[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(6): 980−984.
[5] 谢延敏, 于沪平, 陈 军, 阮雪榆. 韧性断裂准则在板料成形中应用研究进展[J]. 哈尔滨工业大学学报, 2009, 41(1): 169−173. XIE Yan-min, YU Hu-ping, CHEN Jun, RUAN Xue-yu. Recent research advance of application of ductile fracture criteria in sheet metal forming process[J]. Journal of Harbin Institute of Technology, 2009, 41(1): 169−173.
[6] 李 磊, 周晚林, HUSSAIN G. 金属板料单点渐进成形极限的数值模拟预测[J]. 机械工程学报, 2010, 46(18): 102−107. LI Lei, ZHOU Wan-lin, HUSSAIN G. Prediction of single point incremental forming limit[J]. Journal of Mechanical Engineering, 2010, 46(18): 102−107.
[7] 黄晓忠, 陈劼实, 陈 军. 板料冲压成形破坏判断准则的研究进展[J]. 机械工程学报. 2011, 47(4): 23−31. HUANG Xiao-zhong CHEN Jie-shi CHEN Jun. Review on fracture criterion of sheet metal forming[J]. Journal of Mechanical Engineering, 2011, 47(4): 23−31.
[8] WANG K, WIERZBICKI T. Experimental and numerical study on the plane-strain blanking process on an AHSS sheet[J]. International Journal of Fracture, 2015, 194(1): 19−36.
[9] Oyane M, Sato T, OKIMOTO K, SHIMA S. Criteria for ductile fracture and their applications[J]. Journal of Mechanical Working and Technology, 1980, 4(1): 65−81.
[10] Takuda H, Mori K, FUJIMOTO H, HATTA N. Prediction of forming limit in bore-expending of sheet metals using ductile fracture criterion[J]. Journal of Material Processing Technology, 1999, 92/93: 433−438.
[11] 叶 拓, 王 冠, 姚再起, 李落星. 汽车用 6xxx系铝合金薄壁件的韧性断裂行为. 中国有色金属学报, 2014, 24(4): 878−887. YE Tuo, WANG Guan, YAO Zai-qi, LI Luo-xing. Ductile fracture behavior of 6xxx aluminum alloy thin-walled components of automobile[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(4): 878−887.
[12] 虞 松, 冯维明, 王 戎. 金属韧性断裂准则的实验研究[J]. 锻压技术, 2010, 35(1): 121−124. YU Song, FENG Wei-ming, WANG Rong. Research on ductile fracture criterion in plastic deformation processes[J]. Forging & Stamping Technology, 2010, 35(1): 121−124.
[13] Dong G J, Zhao C C, Cao M Y. Flexible-die forming process with solid granule medium on sheet metal[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(9): 2666−2677.
[14] 曹秒艳, 赵长财, 董国疆, 郝海滨. 基于固体颗粒介质成形工艺筒形件拉深力学分析[J]. 机械工程学报, 2013, 49(2): 42−48. CAO Miao-yan, ZHAO Chang-cai, DONG Guo-jiang, HAO Hai-bin. Mechanical analysis of deep drawing of cylinder based on solid granules medium forming technology[J]. Journal of Mechanical Engineering, 2013, 49(2): 42−48.
[15] Grüner M, Merklein M. Numerical simulation of hydro forming at elevated temperatures with granular material used as medium compared to the real part geometry[J]. International Journal of Material Forming, 2010, 3(1): 279−282.
[16] Ng T T, Zhou W. DEM simulations of bi-disperse ellipsoids of different particle sizes[J]. Comptes Rendus Mecanique, 2014, 342(3): 141−150.
[17] 孙其诚, 金 峰, 王光谦. 密集颗粒物质的多尺度结构[J]. 力学与实践, 2010, 32(1): 10−15. SUN Qi-cheng, JIN Feng, WANG Guang-qian. Dense particulate matter multi-scale structure[J]. Mechanics and Practice, 2010, 32(1) : 10−15.
[18] 赵春来, 臧孟炎. 基于FEM/DEM的轮胎-沙地相互作用的仿真[J].华南理工大学学报, 2015, 43(8): 75−81. ZHAO Chun-lai, ZANG Meng-yan. Simulation of tire-sand interactions based on FEM/DEM[J]. Journal of South China University of Technology (Natural Science Edition), 2015, 43(8): 75−81.
[19] Onate E, Rojek J. Combination of discrete element and finite element methods for dynamic analysis of geomechanics problems[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(27/29): 3087−3128.
[20] 朱桂庆,王 伟,刘 焜. 基于 FEM-DEM 的三体摩擦界面中接触行为与应力的多尺度分析[J]. 应用力学学报, 2013, 30(3): 316−322. ZHU Gui-qing, WANG Wei, LIU Kun. The multi-scale analysis of contact behavior and stress in the three-bodies tribological interface based on FEM-DEM[J]. Chinese Journal of Applied Mechanics, 2013, 30(3): 316−322.
[21] Savkoor A R, Briggs G A D. The effect of tangential force on the contact of elastic solids in adhesion[J]. Proceedings of the Royal Society of London A: Mathematical Physical & Engineering Sciences, 1977, 356: 103−114.
[22] 曹秒艳, 董国疆, 赵长财. 基于离散元法的固体颗粒介质传力特性研究[J]. 机械工程学报, 2011, 47(14): 62−69. CAO Miao-yan, DONG Guo-jiang, ZHAO Chang-cai. Research on pressure-transfer characteristics in the solid granule medium forming based on the discrete element method[J]. Journal of Mechanical Engineering, 2011, 47(14): 62−69.
[23] 苌群峰, 彭颖红, 杜朝辉.镁合金板材温热成形韧性破裂准则[J]. 机械工程学报, 2009, 45(10): 294−299. CHANG Qun-feng, PENG Ying-hong, DU Zhao-hui. Ductile fracture criterion for warm deep drawing of magnesium alloy sheet[J]. Journal of Mechanical Engineering, 2009, 45(10): 294−299.
(编辑 何学锋)
Forming limit prediction in flexible die forming of AZ31B sheet based on combination of DEM-FEM
CAO Miao-yan1, LI Jiang-chao2, YUAN Ya-ning2, ZHAO Chang-cai2, DONG Guo-jiang3
(1. National Engineering Research Center for Equipment and Technology of Cold Strip Rolling, Yanshan University, Qinhuangdao 066004, China;2. Key Laboratory of Advanced Forging & Stamping Technology and Science (Yanshan University),Ministry of Education, Qinhuangdao 066004, China;3. College of Vehicles and Energy, Yanshan University, Qinhuangdao 066004, China)
For discrete property of solid granules and continuous deformation of sheet metal in the solid granule medium forming (SGMF) process, a simulation model combination of discrete element method and finite element method (DEM-FEM) was proposed and established. Ductile fracture criteria of magnesium alloy sheet warm forming was also established, and its validity was verified combining experiment with finite element simulation. Furthermore, the cylindrical part of AZ31B magnesium alloy with SGMF process was simulated based on DEM-FEM and the experiment was carried out. The results show that, the analysis method of DEM-FEM based on ductile fracture criteria can effectively predict the forming limit of magnesium alloy sheet warm forming with the solid granule medium.
discrete element; finite element; magnesium alloy; solid granule medium; forming limit
Projects(51305385, 51305386) supported by the National Natural Science Foundation of China; Project(QN20131080) supported by the Science Research Youth Foundation of Hebei Province Universities, China
2016-01-25; Accepted date:2016-06-06
ZHAO Chang-cai; Tel: +86-13633333873; E-mail: zhao1964@ysu.edu.cn
10.19476/j.ysxb.1004.0609.2017.04.001
1004-0609(2017)-04-0675-09
TG386.43
A
国家自然科学基金资助项目(51305385,51305386);河北省高等学校科学技术研究青年基金项目(QN20131080)
2016-01-25;
2016-06-06
赵长财,教授,博士;电话:13633333873;E-mail: zhao1964@ysu.edu.cn

