基于双原子库稀疏分解的力学式纸浆浓度传感器测量值补偿研究

周 强 王亚波，* 王 莹 吴 祎

(1.陕西科技大学电气与信息工程学院，陕西西安，710021；2.陕西科技大学材料科学与工程学院，陕西西安，710021)

基于双原子库稀疏分解的力学式纸浆浓度传感器测量值补偿研究

周 强1王亚波1，*王 莹2吴 祎1

(1.陕西科技大学电气与信息工程学院，陕西西安，710021；2.陕西科技大学材料科学与工程学院，陕西西安，710021)

针对目前广泛使用的力学式纸浆浓度传感器测量精度较低的问题，通过研究纸浆纤维结构和力学式纸浆浓度传感器测量原理，发现了这种传感器测量精度较低的原因：第一，纸浆浓度测量信号中噪声信号难以滤除；第二，纸浆流速对纸浆浓度测量影响较大。为此，在研究纸浆浓度测量信号中噪声信号及其性质并建立纸浆浓度传感器测量模型的基础上，提出了利用稀疏分解消除纸浆浓度测量信号中各种噪声信号，同时利用纸浆浓度传感器测量模型对纸浆浓度测量值进行流速补偿。结果表明，该方法能够显著提高纸浆浓度传感器的测量精度。

纸浆浓度测量精度；噪声信号；稀疏分解；流速补偿

在造纸过程中，纸浆流量和纸浆浓度是检测最频繁的2个重要指标[1-2]。纸浆流量的实时、精确测量不仅是流量控制和绝干纸浆纤维计量的先决条件，而且对于提高洗浆、打配浆、抄纸、流送等环节的生产效果[3]，保障成纸质量，提高制浆和抄纸工段的工作效率等影响显著[4]。

目前，用于造纸生产线上的纸浆浓度测量方法有γ射线法、电容法、超声波法、光学法和力学法等[5]。其中，γ射线法、电容法、超声波法的测量精度较高，但γ射线法成本很高，电容法测量范围小，超声波法的测量结果易受到气泡的干扰。因此，对于2%～6%的中浓纸浆，当前广泛使用的浓度测量方法还是力学方法。力学法可分为外旋式、内旋式、静刀式和动刀式4种方法，其中静刀式浓度传感器的使用范围最广，但该浓度传感器在测量过程中会受到纸浆流速变化的影响[6]，同时浓度传感器产生的浓度噪声信号也会对纸浆浓度测量产生一定影响，使得力学式浓度传感器测量精度的提高缓慢甚至趋于停滞不前。

笔者在研究力学式纸浆浓度传感器测量原理的基础上，建立这类传感器的测量模型，并结合纸浆纤维结构特点，获得纸浆浓度信号组成成分及各成分的数学模型和特性。利用以上研究结果对纸浆浓度测量值进行补偿。首先，根据纸浆浓度信号中不同噪声的特性，建立具有尺度特性和无尺度特性的2个原子库，利用这2个原子库中的原子对纸浆浓度信号分别进行稀疏分解和稀疏表示，分离并消除纸浆浓度信号中的噪声信号，最后根据力学式浓度传感器测量模型对纸浆浓度测量值进行流速补偿，从而提高纸浆浓度传感器测量精度。

1 纸浆浓度测量误差的研究

在一定体积的纸浆纤维、水以及气泡的三相混合液中，纸浆纤维的质量百分比，即为纸浆浓度，计算见式(1)：

(1)

因此，纸浆纤维的质量决定了纸浆浓度的大小，且纤维结构会影响纸浆浓度的分布。

1.1纸浆纤维结构特点

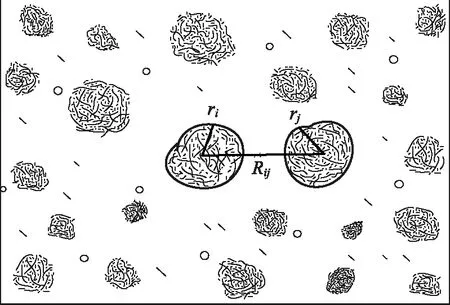
图1 纸浆纤维结构示意图

纸浆是由纸浆纤维、气泡和水组成的三相流体，由于纸浆纤维和气泡在纸浆中的分布具有随机性，造成了纸浆纤维和气泡在纸浆中的分布不均匀。图1反映了纸浆中的纤维(游离纤维与纤维团)及气泡的具体分布情况。纸浆纤维最主要的一个特点就是其在纸浆中会聚集成为纤维团，而纤维团则在纸浆中自由移动、随机分布。有研究表明[7]，纸浆状态的改变会引起纸浆纤维形态的变化。

纤维团的半径r与纤维团的中心间距R是服从一定分布规律的随机变量，能够反映纸浆纤维的形态和结构。据此，建立以下关于纸浆纤维团半径和纤维团中心间距的数学分布模型：

(2)

(3)

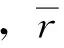
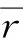
1.2力学式纸浆浓度传感器测量原理

力学式纸浆浓度传感器由敏感元件、机械位移系统和位移测量装置等几部分组成，根据力学平衡原理工作。

纸浆作为一种非牛顿流体中的宾汉流体，其在直管道中流动时会在静置于管道中的敏感元件表面形成层流并产生切向的剪应力f，f由杠杆传递到位移测量装置上，引起位移测量装置的位移Δx，最终产生传感器输出信号s，即纸浆浓度测量值。

一方面，f与纸浆动力黏度μ、纸浆密度ρ和纸浆流速v具有如下关系：

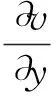
(4)

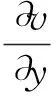
另一方面，传感器输出信号s与Δx及f之间均呈线性关系：

s∝f∝Δx

(5)

当纸浆这种非牛顿流体流动时，会表现出像牛顿流体一样的线性特性[8]。因此，结合式(4)和式(5)得到浓度测量值s与纸浆黏度、密度和流速的关系式：

(6)

式中，K为常数。

由于在一定的纸浆浓度范围内，纸浆黏度μ和纸浆浓度c具有近似的线性关系：

μ=ac+ac0

(7)

式中，c0为纸浆浓度的截距；a为比例系数。

将式(7)代入 式(6) ，且由于纸浆密度ρ基本恒定，因此有：

(8)

其中：

(9)

由式(8)可知，力学式纸浆浓度传感器测量值s与纸浆浓度c直接相关。

1.3纸浆浓度测量误差分析

力学式纸浆浓度传感器测量纸浆浓度的误差是由两个原因造成的，一是纸浆流速变化对纸浆浓度测量的影响；另一个是由于纸浆浓度信号中噪声信号较为复杂且幅度较大，噪声信号与纸浆浓度真实值耦合在一起，影响了纸浆浓度的测量，为此必须研究纸浆浓度信号组成。

1.3.1纸浆浓度信号组成

纸浆浓度信号中含有两种噪声信号。一种是固有噪声信号α(t)，由纸浆纤维结构特点可知：纸浆纤维是以团聚方式存在于纸浆中，使得纸浆浓度分布不均匀，在纸浆纤维团聚处纸浆浓度大，而游离纤维、水和气泡处的纸浆浓度较小，从而造成了纸浆浓度的波动，从信号的角度看就是噪声，称之为固有噪声信号，这种噪声信号是对纸浆物质分布不均匀的真实反映；另一种噪声信号是量测噪声信号β(t)，它是由于浓度传感器机械部分的振动、电路部分电子元件热噪声等因素造成的，与纸浆自身性质无关。

由于浓度真实值是一个变量，称之为浓度趋势项，因此，浓度传感器产生的浓度信号由趋势项c(t)、固有噪声信号α(t)和量测噪声信号β(t)组成。其组成方式并不简单，有研究表明，纸浆浓度的2种噪声信号以线性和非线性方式相互耦合，并以加性方式与趋势项耦合[5]，纸浆浓度信号的数学模型为：

s(t)=c(t)+α(t)+β(t)+γα(t)β(t)

(10)

其中，γ是纸浆浓度固有噪声信号和量测噪声信号的非线性耦合系数。

一般来说，α(t)幅度较大，其幅值完全决定于纸浆浓度自身的性质，而β(t)只取决于浓度传感器的性能，通常精度等级越高的传感器，β(t)越小，但不可能完全消除。正是由于这2种噪声信号的存在，纸浆浓度真实值难以获得。

1.3.2纸浆流速误差

由式(8)可知，纸浆浓度的测量值与纸浆流速v直接相关，传统的浓度测量方法中都是将纸浆流速v看作定值。但实际生产过程中，纸浆流速难以保持恒定。理论计算可知，1%的流速波动会引起1.5%的纸浆浓度测量误差，因此纸浆流速变化对纸浆浓度测量的影响不容忽视。

2 纸浆浓度测量误差补偿

2.1基于稀疏分解的纸浆浓度信号消噪

2.1.1纸浆浓度固有噪声信号和量测噪声信号的性质

由于固有噪声信号α(t)和量测噪声信号β(t)的性质并不相同，传统的消噪方法，在未知纸浆浓度中噪声性质的情况下，盲目地采用低通滤波的方法消除纸浆浓度噪声信号，滤波效果较差[9]。因此，需要研究纸浆浓度信号中噪声信号的性质。

(1)噪声信号的高斯性。噪声信号的高斯性是确定噪声处理方法的前提条件，信号分析领域的大多数噪声处理方法对于非高斯噪声都无效[10]。

通过对固有噪声信号和量测噪声信号的4阶统计量峰度和3阶统计量偏度的计算得知，固有噪声信号呈高斯分布，而量测噪声信号呈非高斯分布。因此，以常规方法来假设传感器量测噪声是高斯噪声必然会造成浓度信号处理的较大误差。

(2)噪声信号的平稳随机性。平稳随机性就是随机过程的统计时不变的特性。由于数学模型是时变的，因此固有噪声和量测噪声都不具有平稳随机性，但从噪声模型的时变速度来看，两者还是有差别的。固有噪声是一种模型惯性较大的有色噪声，模型变化速度缓慢，在较短的时间内，可近似为平稳随机过程；而量测噪声因为模型惯性小、变化快，更接近于非平稳白噪声，其非平稳性较强。

(3)噪声信号的尺度特性。固有噪声信号是纸浆纤维结构分布不均匀的反映，随着外界条件的变化，噪声曲线会发生整体的伸缩变化，即具有尺度特性；而量测噪声信号与纸浆特性无关，无尺度特性。正是由于纸浆浓度固有噪声信号和量测噪声信号在高斯性、平稳随机性和尺度特性上的差别，不能使用相同的方法将其与浓度趋势项分离。

本研究利用稀疏分解能够根据对象不同而灵活构建基函数的特性[11]，针对两种噪声的不同性质，特别是尺度特性的差别，分别构建具有尺度特性和无尺度特性的过完备原子库，并在这2个原子库上分解2种噪声，将这2种噪声从浓度信号中有效分离。

2.1.2建立具有尺度特性和无尺度特性的2个过完备原子库

纸浆浓度信号中2种噪声由于来源不同，特性上的最大差别在于是否具有尺度特性，据此构建具有尺度特性的原子库M1和非尺度特性的原子库M2。M1原子库中的原子主要包括：Gauss函数、Morlet函数、Haar函数等具有尺度特性的基函数；M2原子库中的原子主要包括：冲击函数、Daubechies函数等无尺度特性的函数。

2.1.3噪声信号的稀疏分解

(1)纸浆浓度固有噪声信号的稀疏表示。由于纸浆浓度固有噪声信号α(t)具有一定的尺度特性，本研究采用尺度特性原子库M1对其进行稀疏分解，具体过程如下。

算法初始化时，设纸浆浓度信号s(t)=R1，基于具有尺度特性的原子进行稀疏分解，稀疏分解序号j=1。

(11)

(12)

(13)

(14)

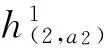
(15)

稀疏分解的终止条件是：

(16)

RJ+1s≈c(t)+Δd(v)+β(t)+λα(t)β(t)

(17)

(2)纸浆浓度量测噪声信号的稀疏表示。利用非尺度特性的原子库M2中的原子对RJ+1s进行稀疏分解。

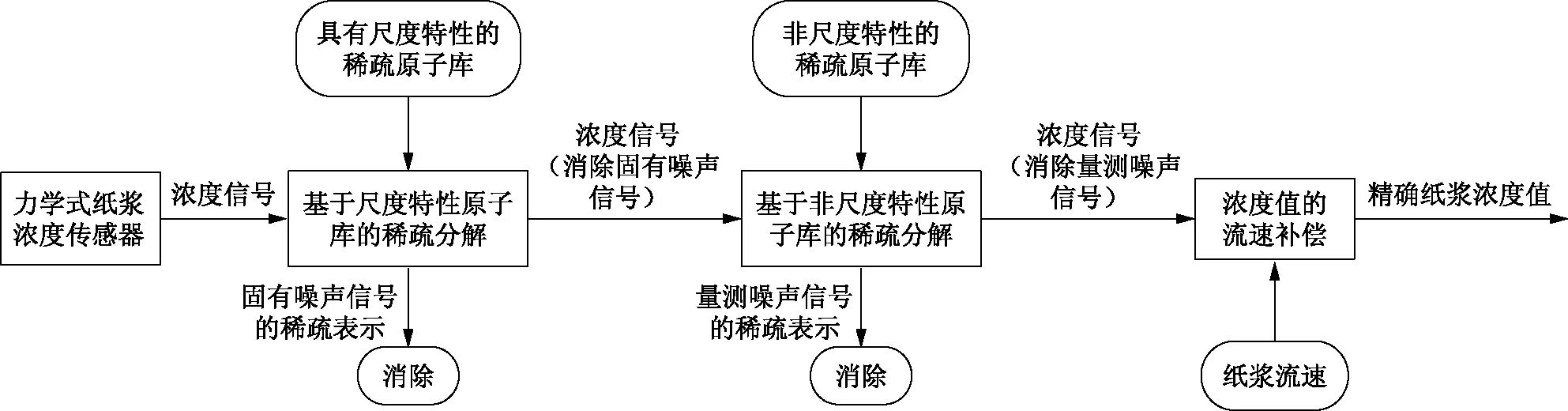
图2 力学式纸浆浓度传感器浓度信号处理过程

首先，稀疏分解序号i=1，

|〈RJ+1s，y1〉|=sup|〈RJ+1s，yi〉|

(18)

该过程选中的第一个原子是y1，

RJ+1s=〈R0s′，y1〉y1+R1s′

(19)

其中，R1s′是用最佳原子y1对RJ+1s进行最佳匹配后的残余部分，对其继续进行稀疏分解，直至：

〈RJ+1s′，yi〉≤const2

(20)

获得稀疏表示：

(21)

RIs′≈c(t)+Δd(v)

(22)

2.2纸浆流速补偿

根据式(8)对纸浆流速变化进行补偿，补偿过程为：

(1)纸浆浓度标定。已知浓度传感器的纸浆浓度截距c0和比例系数a，在纸浆流速恒定的条件下，记录纸浆浓度测量值s、浓度真实值c以及纸浆流量传感器测量的流量值v0(纸浆的标定流量)，将其作为v，代入式(8)中，计算出K′。

(2)纸浆流速补偿。将当前纸浆流速v带入式(8)，就可以获得经过流速补偿的纸浆浓度sb：

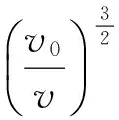
(23)

其中，s为补偿前的纸浆浓度测量值。

2.3纸浆浓度测量补偿流程

本研究提出的对力学式纸浆浓度传感器输出信号的处理过程如图2所示。处理过程包括：①基于尺度特性原子库的稀疏分解、稀疏表示并消除固有噪声信号；②基于非尺度特性原子库的稀疏分解、稀疏表示并消除量测噪声信号；③纸浆流速补偿。

3 浓度测量实验

在实验室条件下以1.2%～3.0%浓度的化学浆为测量对象，用于纸浆浓度测量的是SBT-2400型智能定刀式纸浆浓度传感器，真实值为实验室化验值。

浓度传感器输出的纸浆浓度测量值见图3。由图3可知，原始浓度信号含有浓度趋势项、浓度固有噪声信号和量测噪声信号。

3.1基于低通滤波和小波分解的纸浆浓度处理过程和效果

纸浆浓度处理方法包括传统的低通滤波和目前研究较多的小波分解及本质模态分离(EMD)法等。低通滤波方法的处理结果如图4所示。由图4可见，该方法难以全部消除纸浆浓度信号中的噪声信号。

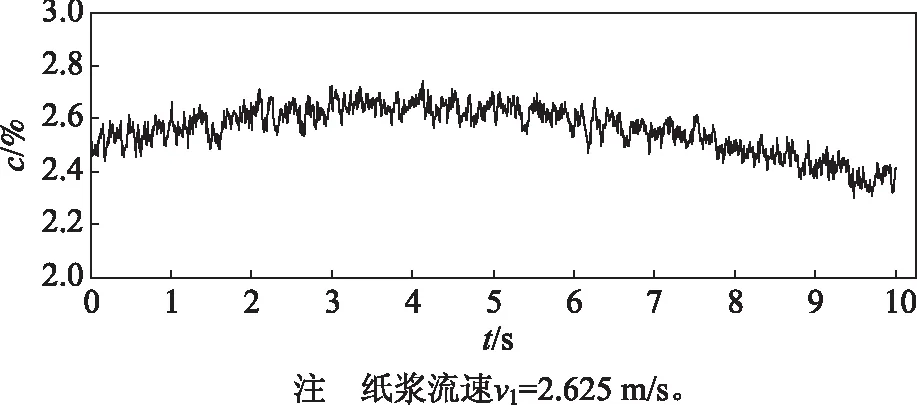
图3 纸浆浓度测量值

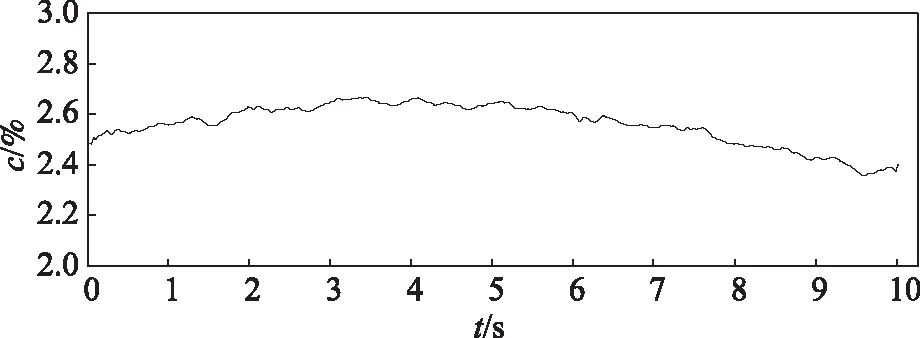
图4 经低通滤波处理后的纸浆浓度曲线

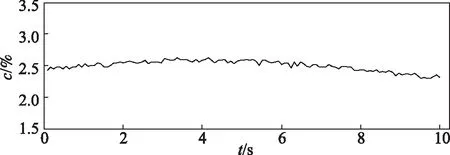
图5 经小波分解处理后的纸浆浓度曲线

图5是经过4层Symlet小波分解处理后的纸浆浓度曲线图。实验表明，4层以上的小波分解去除噪声信号的效果趋于饱和，但由于选择母小波函数的盲目性以及母小波函数的单一性，该方法还是难以完全消除纸浆浓度信号中的噪声信号。

3.2基于双原子库稀疏分解和流速补偿的纸浆浓度噪声信号分离过程和效果

首先，利用具有尺度特性的原子库M1中的原子对纸浆浓度信号进行稀疏分解和稀疏表示并消除其中固有噪声信号，处理过程见图6(a)～图6(d)；然后，利用非尺度特性的原子库M2中的原子对纸浆浓度信号进行稀疏分解和稀疏表示并消除其中量测噪声信号，处理过程见图6(e)～图6(f)；最后根据纸浆流速采用式(23)对纸浆流速进行补偿，获得消除噪声信号后的纸浆浓度曲线，见图6(g)。

3.3实验结果

各纸浆浓度信号处理方法的处理效果比较如表1所示。由表1可知，基于双原子库稀疏分解的力学式纸浆浓度传感器测量值补偿方法可以将纸浆浓度的绝对测量误差减小到0.01%以下，相对误差减小到0.4%以下，绝对误差和相对误差均低于传统的低通滤波消噪方法和小波分解处理方法。

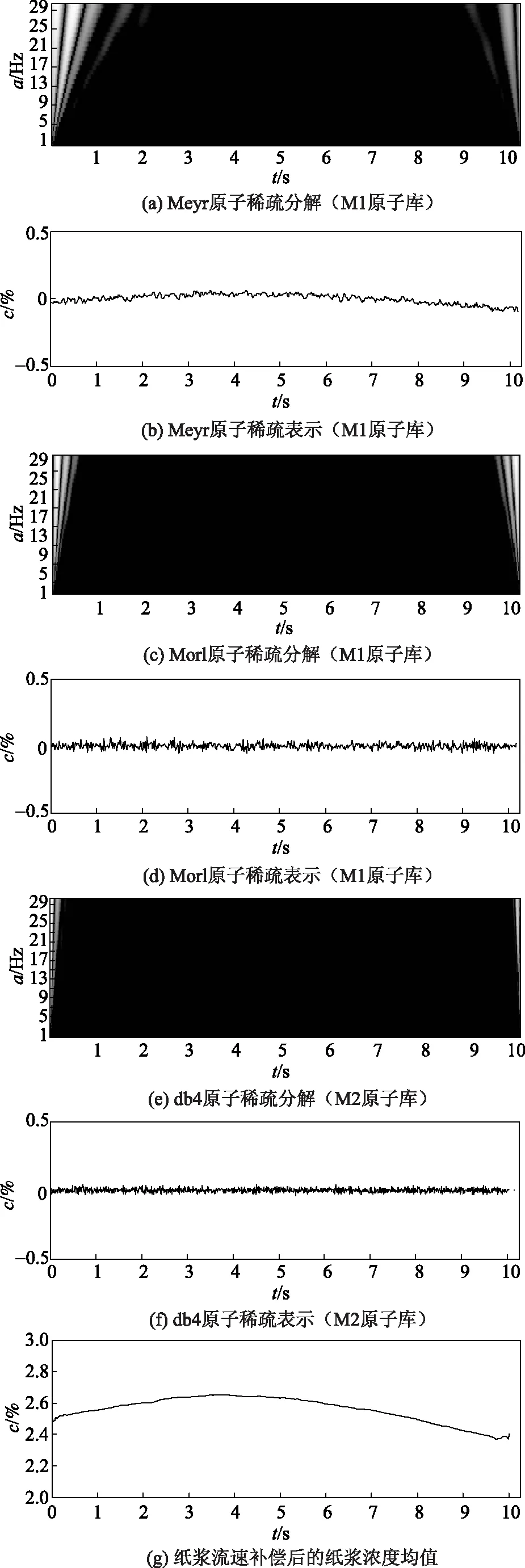
图6 基于双原子库稀疏分解的纸浆浓度测量值补偿

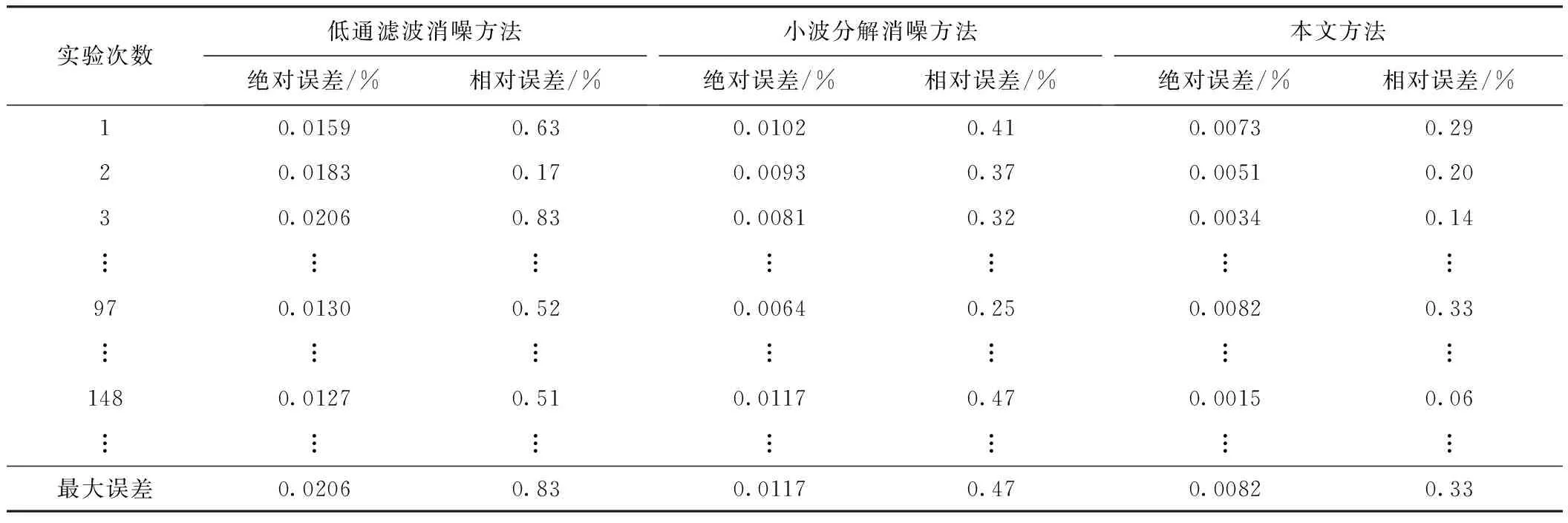
表1 纸浆浓度信号处理效果比较

4 结 论

在研究纸浆浓度信号成分及噪声信号特性的基础上，提出了利用双原子库的稀疏分解方法消除纸浆浓度信号中的各种噪声信号，同时通过纸浆流速补偿，解决当前力学式纸浆浓度传感器测量精度低的问题。文中具体讲述了不同噪声信号在其原子库下的稀疏分解和表示过程及纸浆流速补偿过程，并通过浓度测量实验表明在未增加硬件的前提下，本文方法能够有效分离纸浆浓度信号中的噪声信号，精确补偿纸浆浓度流速误差，从而使得力学式浓度传感器达到较高的测量精度。

[1] 叶道星,李 红.中浓度纸浆流态化特征[J].江苏大学学报,2015,36(3):276．

[2] 黄亚南,张爱娟,胡慕伊.基于单神经元PSD的纸浆浓度控制算法研究[J].中国造纸,2016,35(5):46.

[3] Richard J.Kerekes.Quantifying the Pulp Refining Process[J].Paper and Biomaterials,2016,1(1):38．

[4] Goncharenko I A,Konoiko A I,Polikanin A M.Liquid concentration sensor based on slot waveguide microresonators[J].Measurement Techniques,2010,34(8):535．

[5] 石春鹤,陈冠魁,韩晓微.外旋式纸浆浓度变送器的改进与应用[J].中国造纸学报,2014,29(4):40．

[6] 赵 冲.静刀式纸浆浓度变送器流速补偿的研究[J].计算机与数字工程,2012,40(3):115．

[7] 周 强,韩九强.提高力学法测量纸浆浓度精度的研究[J].中国造纸学报,2008,23(2):100．

[8] 叶道星,李 红,邹晨海.中浓度纸浆流态化特征[J].江苏大学学报:自然科学版,2015(3):276．

[9] Zhou Qiang.Soft measurement of pulp suspension flow velocity based on wavelet transform[J].Can J Chem Eng,2010,88(1):879．

[10] Bakrim M,Aboutajdine D.Higher-order statistics based blind estimation of non-Gaussian bidimensional moving average models[J].Signal Processing,2006,86(10):3031．

[11] Zhao Yuanjun,Wu Zhilu.A novel signal sparse decomposition based on modulation correlation partition[J].Neurocomputing,2016,171(7):171．

Abstract：To solve the problem of low measuring precision in the mechanical consistency sensor widely used for pulp at present,by studying the pulp fiber structure and mechanical consistency sensor measuring principle,reasons of effecting the sensors measurement precision were found.First,the noise signal was difficult to filter out from the measurement signal of the pulp consistency.Second,the pulp flow velocity had a great effect on the pulp consistency measurement.Based on the study of noise signal and its nature and the establishment of consistency sensor measurement model,sparse decomposition was used to eliminate all kinds of noise from the pulp consistency signal.At the same time,consistency sensor measurement model was used to compensate the effect of pulp flow rate on the measured consistency value.Experiment results showed that this method could significantly improve the pulp consistency measuring accuracy.

Keywords：pulp consistency measuring accuracy; noise signal; sparse decomposition; flow velocity compensation

(责任编辑：陈丽卿)

MeasuredValueCompensationofMechanicalConsistencySensorUsedforPulpBasedonDoubleAtomLibrarySparseDecomposition

ZHOU Qiang1WANG Ya-bo1,*WANG Ying2WU Yi1

(1.InstituteofElectricalandInformationEngineering,ShaanxiUniversityofScience&Teacnology,Xi’an,ShaanxiProvince,710021; 2.MaterialScienceandEngineeringInstitute,ShaanxiUniversityofScience&Technology,Xi’an,ShaanxiProvince,710021)(*E-mail:1123594885@qq.com)

TS73

A

1000-6842(2017)03-0052-06

2016-08-04

陕西省教育厅专项科技项目(16JK1105)；陕西省科技攻关项目(2016GY-005)。

周 强，男，1969年生；博士，教授；主要研究方向：智能信息处理技术。

*通信联系人：王亚波，E-mail：1123594885@qq.com。