基于“边界层”理论的纸张干燥动力学模型及其数值仿真

陈晓彬 董云渊 郑启富 余建刚 李继庚 刘焕彬

(1.衢州学院化学与材料工程学院，浙江衢州，324000；2.华南理工大学制浆造纸工程国家重点实验室，广东广州，510640)

基于“边界层”理论的纸张干燥动力学模型及其数值仿真

陈晓彬1董云渊1郑启富1余建刚1李继庚2刘焕彬2

(1.衢州学院化学与材料工程学院，浙江衢州，324000；2.华南理工大学制浆造纸工程国家重点实验室，广东广州，510640)

利用“边界层”理论推导出纸张表面水分蒸发动力学模型，建立了纸张干燥过程物料与能量衡算模型，并采用数值分析方法，模拟某一瓦楞纸机的干燥过程，得到纸张在干燥过程中的温湿度变化曲线以及水分蒸发速率变化曲线，并定量分析了该干燥过程纸张干燥的3个阶段：升温干燥阶段(1#～4#烘缸)、恒速干燥阶段(5#～39#烘缸)、减速干燥阶段(40#～48#烘缸)。当纸张湿含量下降到0.22 kg/kg时，进入减速干燥阶段。在线测量结果与模型仿真结果的对比分析表明，模拟结果和实际在线测量结果非常接近，验证了基于“边界层”理论推导的纸张干燥动力学模型的准确性。

纸张干燥；水分蒸发速率；数值仿真

造纸过程的本质是一个脱水过程，该过程主要通过纸机的3部分完成：成形部、压榨部和干燥部[1]。成形部主要借助重力作用将湿纸幅的干度提升至15%～25%；压榨部通过机械作用进一步将湿纸幅干度提升至33%～55%；干燥部通过消耗热能的蒸发作用脱除纸张内水分，使成品纸达到干度要求，约90%～95%[2]。干燥部脱水量约为上网浆料总含水量的1%，是纸机脱水量最少的工段，但其脱水成本最高[3]。以长网纸机为例，干燥部的质量约占纸机总质量的60%～70%，其长度约占纸机总长度的60%，投资成本约占整个纸机投资成本的40%[1]。据IPST(Institute of Paper Science and Technology，造纸科学与技术研究所)的研究[4]，干燥部的能耗约占纸机总能耗的61.9%。因此，无论从干燥部的质量、长度、投资成本还是能耗水平考虑，干燥部均是纸机最关键的部位。

目前，工业界和学术界常采用2种动力学模型来确定纸张干燥过程中的水分蒸发速率：一种是工艺计算手册提供的经验公式(见式(1))[5]，另一种是基于扩散理论的Fick定律(见式(2))[6-9]。

(1)

式中，Vevap表示蒸发速率，kg/(m2·h)；K表示总传热系数，kJ/(m2·h·℃)；Ts表示烘缸内加热蒸汽的温度，℃；Tp表示纸张温度，℃；r表示蒸发水分的热焓，kJ/kg；Kn表示自由表面蒸发系数，Kn=0.0229+0.174v，v表示蒸发表面的空气流速，m/s；PS表示蒸发温度下饱和蒸汽压，Pa；PD表示外界空气的水蒸气分压，Pa；P表示外界大气压，Pa。

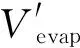
(2)

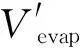
经验公式忽略了传热和传质相互耦合的影响以及减速干燥阶段吸附热的影响等问题，简化了模型，有助于解决一些大尺度的设计问题，但要模拟某一生产过程，其精度是不够的。Fick定律是基于扩散介质相对静止的假设条件获得的，这显然和实际生产过程中纸张的高速运动相差较大。因此，建立一个能够真实描述纸张干燥过程水分蒸发速率的动力学模型已成为造纸科技工作者的研究热点。

为解决上述问题，笔者利用“边界层”理论，从纸张干燥过程的传热传质机理出发，推导出基于“边界层”理论的纸张表面水分蒸发动力学模型，基于该模型构建纸张干燥过程物料与能量衡算模型，并采用数值分析方法模拟纸张干燥过程的温湿度变化以及水分蒸发速率的变化。“边界层”理论是德国物理学家Ludwig Prandtl于1904年提出的，主要用于研究水和空气等黏度很小的流体在大雷诺数下绕物体流动过程中的传热传质问题。笔者通过理论计算发现，在空气温度60℃、相对湿度60%、烘缸直径1.8 m条件下，纸机车速只要大于304.57 m/min时(取特征长度为烘缸直径)，纸张表面附近雷诺数大于105，处于湍流状态，正符合“边界层”理论的研究范围。

1 纸张干燥过程

1799年，法国人Louis Rrobert发明了连续抄纸机后，但直到1816年连续抄纸机才装配有烘缸，实现了连续生产干的纸产品的生产工艺[10]。经多年发展，涌现了一批新的干燥工艺，如OptiDry干燥工艺、HiDryer干燥工艺、Yankee干燥工艺、红外干燥工艺、冲击干燥工艺等，但除了卫生纸采用Yankee干燥工艺干燥、涂布纸采用冲击干燥或红外干燥工艺干燥外，目前行业内采用最多的干燥工艺仍是传统的多烘缸干燥工艺。该干燥工艺中，纸张有2种干燥方式(见图1)，即对流干燥(AB段)和接触干燥(BC段)，干燥区长度LAB和LBC可通过式(3)计算得到[11]。

(3)

式中，LAB表示对流干燥区长度，m；LBC表示接触干燥区长度，m；D表示烘缸直径，m；L1表示同排相邻两烘缸中心水平距离，m；L2表示上下两排烘缸中心垂直距离，m。

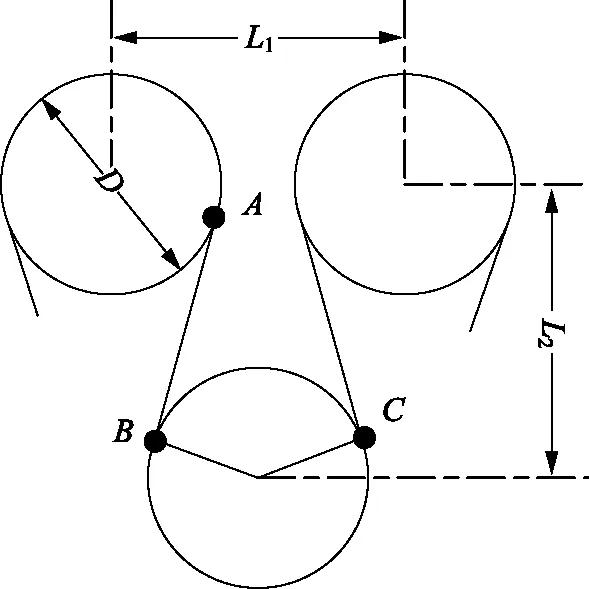
图1 多烘缸干燥工艺烘缸排布结构

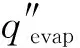
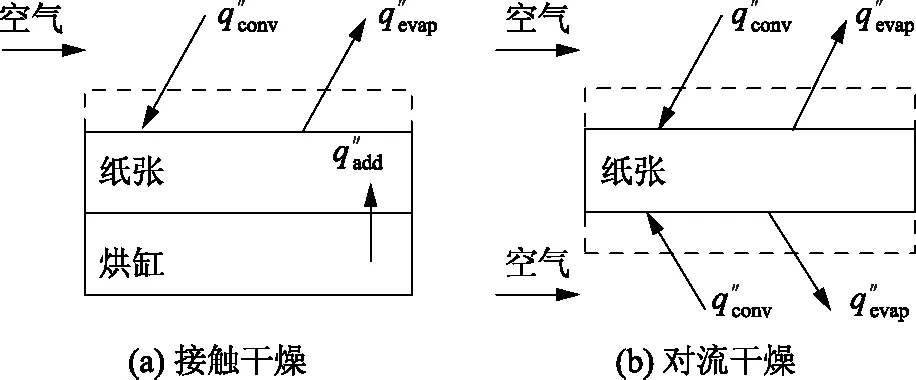
图2 蒸发过程能流分析

2 纸张表面水分蒸发动力学模型的推导

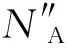
(4)

(5)

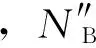
根据守恒定律，则总物料的摩尔流密度N″为：

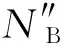
(6)

式中，N″表示总物料的摩尔流密度，mol/(m2·s)；C表示总物料的摩尔浓度，mol/m3；v表示总物料的平均速度，m/s。

总物料的平均速度v为：

v=xA·vA+xB·vB

(7)

式中，xA和xB分别表示水分和空气的摩尔分数。

则，水分相对总物料平均速度的摩尔流密度，即扩散摩尔流密度jA为：

jA=CA·(vA-v)

(8)

式中，jA表示水分相对总物料平均速度的摩尔流密度，mol/(m2·s)。

由式(4)和式(8)可得：

(9)

根据Fick定律：

jA=-C·DAB·xA

(10)

式中，DAB表示扩散系数，m2/s；xA表示摩尔分数梯度，m-1。

将式(10)和式(7)代入式(9)中，得：

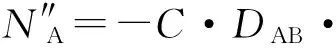
(11)

式(11)指出了影响纸张表面水分蒸发动力的2种因素：①扩散的影响，即由于水分子相对于总物料平均运动的运动；②平行流动的影响，水分随着总物料平均运动一起的运动。

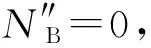
(12)

则：

(13)

纸张表面水分迁移示意图如图3所示，图3中δ表示边界层的厚度，m；xA，0和xA，δ分别表示边界层上下边界上水分的摩尔分数；Δz表示任取的积分微元；z和z+Δz分别表示积分微元的上下界面；Pa表示空气中水蒸气分压，Pa；Pp表示纸张表面水蒸气分压，Pa。任取一个积分段Δz，定常态物料守恒表明，水分进入平面z的量等于离开平面(z+Δz)的量。

(14)

式(14)两边除以Δz，并取Δz→0的极限，得：

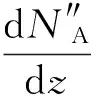
(15)

将式(13)代入式(15)：

(16)

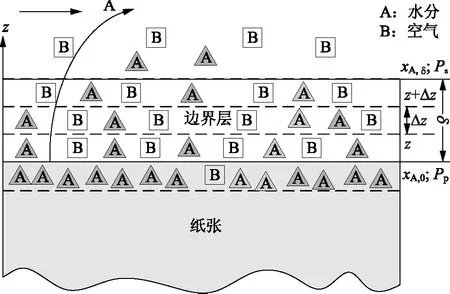
图3 纸张表面水分迁移示意图

根据克拉伯龙方程C=Ptot/RT(Ptot表示总压，Pa；R表示气体常数，R=8.31 J/(mol·K)；T表示温度，K)，而在计算积分的微元空间内，可以认为Ptot和T是不变的，则可近似认为总摩尔浓度C是恒定的。DAB与组分浓度无关，也可近似为常量。简化积分计算过程，式(16)是一个以水分摩尔分数表示浓度梯度的二阶微分方程。

利用边界条件：xA(0)=xA，0，xA(δ)=xA，δ。对z积分求解可以得到：

(17)

根据道尔顿分压定律xA，δ=Pa/Ptot，xA，δ=Pp/Ptot，则，式(17)还可以表示为：

(18)

令DAB/δ=K，即传质系数，则纸张表面水分蒸发动力学模型可表示为：

(19)

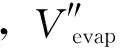
3 纸张干燥过程物料与能量衡算模型的建立

3.1接触干燥

取绝干定量G的纸张为研究对象。如图2所示，接触干燥区有热源且单面自由蒸发。

根据质量守恒：

(20)

式中，G表示纸张绝干定量，kg/m2；u表示纸张湿含量，kg/kg；t表示时间，s。

根据能量守恒：

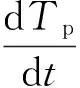
(21)

式中，qadd表示烘缸传给纸张的热量，J/(m2·s)；qconv表示纸张与空气间的对流传热量，J/(m2·s)；qevap表示水分蒸发带走的热量，J/(m2·s)；CF表示绝干纤维比热，取CF=1400 J/(kg·℃)；CW表示水的比热，取CW=4200 J/(kg·℃)。

烘缸传给纸张的热量：

qadd=hcyl-p(Tcyl-Tp)

(22)

纸张与空气间的对流传热：

qconv=hp-a(Tp-Ta)

(23)

蒸发带走的热量：

(24)

式中，ΔHevap表示纸张干燥蒸发热，J/kg。

则接触干燥物料与能量衡算模型为：

(25)

3.2对流干燥

如图2所示，对流干燥区无热源且双面自由蒸发，即qadd=0，根据物料与能量守恒原则，同理可得对流干燥物料与能量衡算模型如式(26)所示。

(26)

4 某瓦楞纸机干燥曲线数值仿真与验证分析

4.1某瓦楞纸机干燥工艺

以某一多烘缸、半密闭气罩的瓦楞纸机干燥部为例，采用数值分析方法，模拟纸张在干燥过程中温度和湿含量的动态变化。该干燥部基本参数如表1所示。

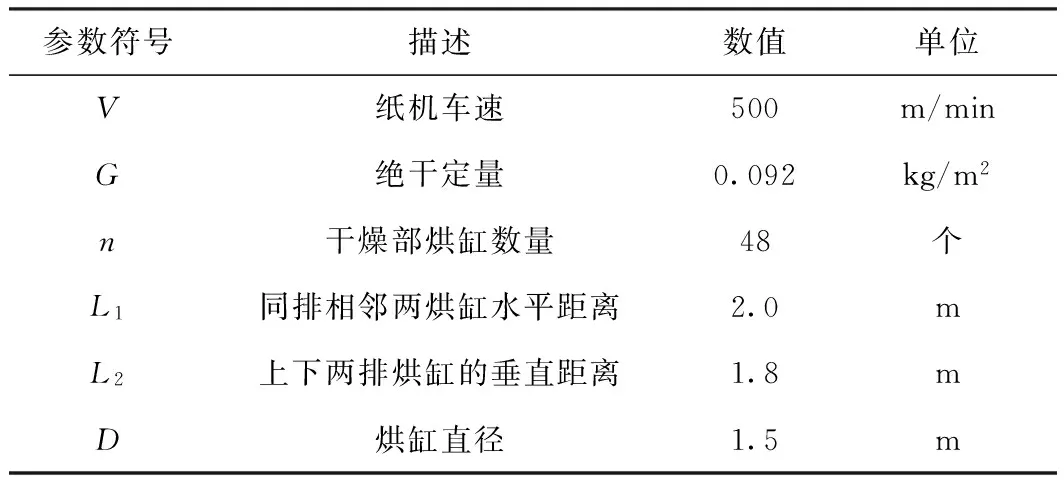
表1 纸机基本参数

采用Swema公司的Temp 20测量该干燥部烘缸表面温度，采用Testo公司的Testo400测量袋区空气的温湿度，测量结果如图4所示。

图4 烘缸表面温度与袋区空气温湿度测量结果

4.2模型求解的初值和边界条件

经过工艺调研，纸张进入干燥部的干度为45%，即湿含量u(0)=1.22 kg/kg；温度为30℃，即Tp(0)=30℃。

纸张是一种吸湿性材料，其表面水蒸气分压(Pp)是纸张温度和湿含量的函数[12]：

Pp=Psat(Tp)·φ(u，Tp)

(27)

饱和水蒸气压力Psat与纸张温度Tp的关系，可用Antoine方程表示：

(28)

φ(u，Tp)是等温吸附曲线，本研究采用Heikkilä[12]提出的计算模型：

φ(u，Tp)=1-exp(-47.58u1.87-0.10085Tpu1.0585)

(29)

纸张中水分的蒸发热ΔHevap由2部分构成：汽化潜热ΔHlat和吸附热ΔHs。

ΔHevap=ΔHlat+ΔHs

(30)

水的汽化潜热跟温度和压力有关，纸张干燥可近似常压，则汽化潜热与温度的关系可通过查表数据回归得到：

ΔHlat=(2504.7-2.4789Tp)×103

(31)

吸附热可用Clausius-Clapeyron方程求解，可得：

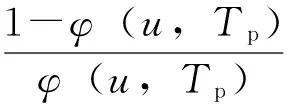
(32)

式中，Rv表示水蒸气常数，Rv=461.52 J/(kg·K)。

4.3仿真结果与验证分析

纸张干燥过程是一个传热与传质相互耦合的复杂过程，建立的物料与能量衡算模型是一个二元常微分方程组，采用Runge-Kutta四阶方法数值求解方程组，各传热传质系数的取值参考文献[8]和文献[10]，如表2所示。数值仿真结果如图5和图6所示。

表2 各传热传质系数

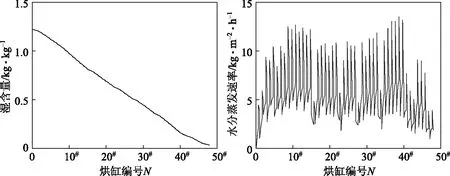
图5 纸张在干燥过程中的温湿度变化曲线及水分蒸发速率曲线

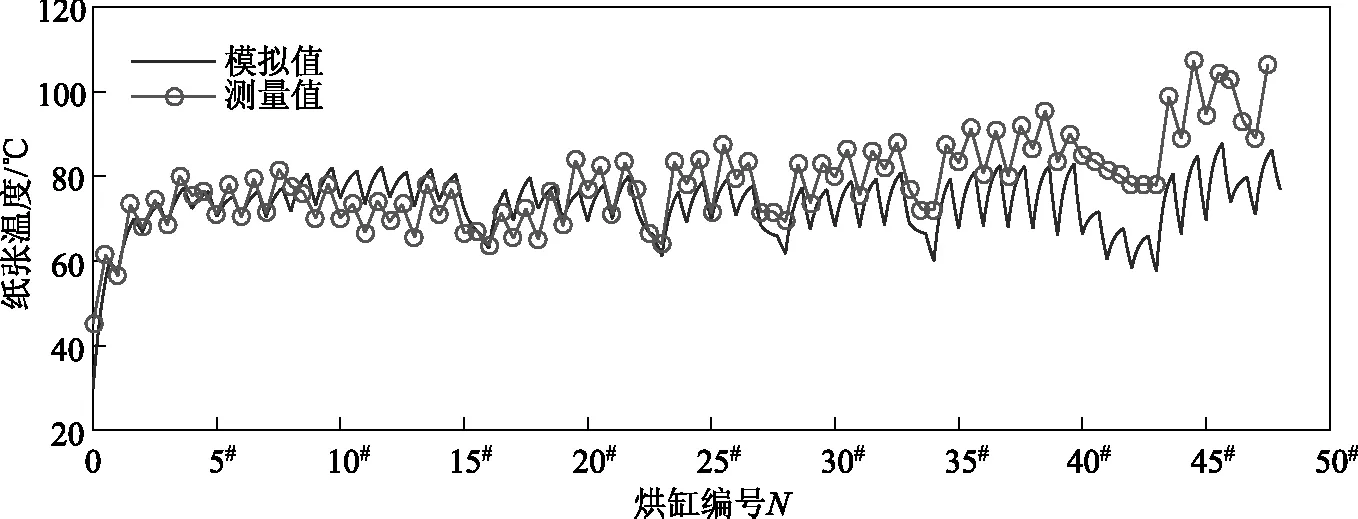
图6 纸张温度模拟值与测量值比较分析

利用基于“边界层”理论的纸张干燥动力学模型模拟得到干燥过程中纸张湿度变化曲线和水分蒸发速率曲线，结果如图5所示。从图5可看出，沿纸机MD方向纸张湿含量的变化趋势大致可分为3个阶段：升温干燥阶段、恒速干燥阶段、减速干燥阶段。从水分蒸发速率变化曲线可以看出，5#～39#烘缸位置属于恒速干燥阶段，1#～4#烘缸位置为升温阶段干燥，40#～48#烘缸位置为减速干燥阶段。40#烘缸位置处的纸张湿含量为0.22 kg/kg(干度约为81.9%)，可知对于该干燥过程，当纸张干度大于81.9%时，纸张进入减速干燥阶段。

采用Fluke公司的IR 574点温仪对纸张温度进行在线测量，以验证仿真结果的准确性。纸张温度模拟值与测量值对比分析如图6所示。由图6可见，模拟结果和实际在线测量结果非常接近，表明基于“边界层”理论推导的纸张干燥动力学模型能够较好地描述纸张干燥过程。

5 结语及展望

利用“边界层”理论，推导了纸张干燥动力学模型，该模型充分考虑了纸张干燥过程传热传质相互耦合的影响，并综合考虑了影响纸张表面水分蒸发动力的2种因素，即①扩散的影响，即水分子相对于总物料平均运动的运动；②平行流动的影响，即水分随着总物料平均运动一起的运动。该模型优于忽略了传热传质耦合影响的经验模型，也优于忽略了平行流动影响的Fick定律模型。

针对2种不同的纸张干燥形式，即有热源的接触干燥和没有热源的对流干燥，依据传热传质基本定律建立了纸张干燥过程物料与能量衡算模型，即一个二元常微分方程组。利用Runge-Kutta四阶方法求解方程组，数值仿真了某一瓦楞纸机干燥过程，获得了纸张在该干燥过程中的温湿度变化曲线以及水分蒸发速率曲线，并定量分析了该干燥过程纸张干燥的3个阶段：升温干燥阶段(1#～4#烘缸)、恒速干燥阶段(5#～39#烘缸)和减速干燥阶段(40#～48#烘缸)。该干燥过程纸张湿含量下降到0.22 kg/kg时，纸张进入减速干燥阶段，此时的纸张湿含量也被称为临界含湿量(CMC，Critical Moisture Content)。纸张干燥经过升温阶段以后，在临界湿含量之前，蒸发动力基本恒定，纸张从环境获得的热量(包括烘缸表面的接触传热和周围空气的对流传热)和水分蒸发消耗的蒸发潜热基本维持动态平衡，纸张温度基本恒定；当纸张达到临界湿含量，纸张表面水分蒸发动力下降，水分蒸发消耗的蒸发潜热和环境给予的热量不能平衡，纸张温度呈上升趋势。在线测量纸张温度与模型仿真结果的对比分析表明，模拟结果和实际在线测量结果非常接近，验证了基于“边界层”理论推导的纸张干燥动力学模型的准确性。

基于“边界层”理论推导的纸张干燥动力学模型能够较好地描述纸张干燥过程，但在建立纸张干燥过程物料与能量衡算模型时仍存在一些不足。衡算模型是以烘缸表面和袋区空气为边界建立的，只能模拟纸张在干燥部的状态变化，不能模拟蒸汽-冷凝水系统、通风与余热回收系统等干燥部子系统，并且模型求解时需要已知烘缸表面温度与袋区空气温湿度的值。而实际生产过程中，纸机一般都没有安装测量烘缸表面温度与袋区空气温湿度的传感器，这使得模型在应用于在线模拟场景时受到很大限制。因此，仍需要开发能够模拟整个纸机干燥部系统的数学模型，并且要选择能够在线测量的变量作为模型的输入变量，这也将是笔者接下来做进一步深入研究的重点。

[1] 卢谦和.造纸原理与工程[M].北京:中国轻工业出版社,2007．

[2] Ghosh A K.Fundamentals of Paper Drying-Theory and Application from Industrial Perspective[M].Croatia:INTECH Open Access Publisher,2011．

[3] 孔令波,刘焕彬,李继庚,等.基于工艺流程的纸机干燥部建模与模拟[J].中国造纸学报,2015,34(4):44．

[4] JACOBS,IPST.Report for pulp and paper industry energy band width study [R].USA:American Institute of Chemical Engineers,2006．

[5] 王忠厚,许志晔,吴毓琳.制浆造纸工艺计算手册[M].北京:中国轻工业出版社,2011．

[6] 卢 涛,沈胜强,李素芬.纸张干燥过程的数值模拟与参数分析[J].中国造纸学报,2003,18(1):124．

[7] 林治作,李继庚,周艳明.双干网多烘缸纸机纸张干燥过程建模研究 [J].造纸科学与技术,2012(3):78．

[8] 孔令波.纸张干燥过程传热传质数学模型的研究[D].广州:华南理工大学,2013．

[9] 周艳明,刘焕彬,李继庚.集成物流、 能流和流分析的纸机干燥部建模[J].中国造纸学报,2014,29(1):33．

[10] 陈克复.制浆造纸机械与设备(下)[M].北京:中国轻工业出版社,2003．

[11] 林治作.纸张干燥过程建模研究[D].广州：华南理工大学,2012．

[12] Heikkilä P.A Study on the Drying Process of Pigment Coated Webs[D].Finland:Åbo Akademi University,1993．

Abstract：A kinetic model of water evaporation on the surface of paper was derived based on the boundary layer theory in the current study.In addition,the mass and energy balance model was established for paper drying process.Using numerical analysis method,a paper drying process of corrugated paper machine was simulated,and the paper temperature,paper moisture,and the drying rate during paper drying process were calculated,three stages during paper drying process were analyzed quantitatively:the temperature-rising drying stage (1#～4#cylinder),the drying at constant rate (5#～39#cylinder) and decelerating drying stage (40#～48#cylinder).When paper moisture dropped to 0.22 kg/kg,the paper entered into the decelerating drying stage.

Keywords：paper drying; evaporation rate; numerical simulation

(责任编辑：陈丽卿)

KineticModelandNumericalSimulationofPaperDryingProcessBaseonBoundaryLayerTheory

CHEN Xiao-bin1,*DONG Yun-yuan1ZHENG Qi-fu1YU Jian-gang1LI Ji-geng2LIU Huan-bin2

(1.CollegeofChemicalandMaterialEngineering,QuzhouUniversity,Quzhou,ZhejiangProvince,324000; 2.StateKeyLabofPulpandPaperEngineering,SouthChinaUniversityofTechnology,Guangzhou,GuangdongProvince,510640)(*E-mail:xbchen24264@163.com)

TS755

A

1000-6842(2017)03-0037-06

2017-04-06

陈晓彬，男，1988年生；讲师；主要从事制浆造纸过程节能与过程优化研究。 E-mail:xbchen24264@163.com