例谈高中数学函数解题思路多元化的方法
⌾韩欣键
例谈高中数学函数解题思路多元化的方法
⌾韩欣键
数学函数知识是高考命题的热点,学生们掌握了函数知识,就相当于掌握了高中数学的半壁江山。基于此,本文分析了高中数学函数知识的重点与难点,并分别从利用发散思维以及创新思维求解数学函数两方面,提出解题思路多元化的方法,提高学生的解题效率,进而提高学生的数学成绩。
高中数学;解题方法;解题思路
前言:升入高中之后,笔者首次接触到了函数知识,在学习函数知识的初期,觉得函数知识并没有教师所说的那么困难,自己也能很快的接受新知识,但是直到亲自动手解决实际的函数问题时,才意识到函数知识并没有想象的那样简单,在解答函数问题时,总会漏掉题目中的隐含关系,致使得出错误的答案,数学成绩也明显下滑。因此,在学习高中数学函数知识的过程中,学生需要熟练掌握函数的解题方法,来提升自身学习数学的能力。
一、高中数学函数知识的重点与难点
1.高中数学函数知识的重点 在学习高中数学函数知识时,要想灵活运用函数知识解决其他数学问题,需要准确把握函数解题的重点知识。学生在函数解题的过程中,需要掌握的重点知识有:函数的概念、函数的性质以及函数图像,其中,定义域与函数解析式求解,是高考考试中的热点问题。函数的三要素之一便是定义域,它在考试中常以选择题或者是填空的形式出现,难度不是很大,但是在实际解决函数的综合问题时,由于定义域具有隐蔽性,很多学生会忽略定义域的限制,得出错误的结果。解析法属于函数表达式的一种,它可以清楚的将各个变量之间的关系呈现出来,通过研究历年的高考题,笔者发现函数解析式求解是历年高考题的常考考点,函数解析式的求解方法多种多样,在求解的过程中,学生应当采用划归、转化以及分类讨论的方法,轻松搞定函数解析式问题。
2.高中数学函数知识的难点 高中数学函数知识的难点主要体现在两个方面,一方面是函数的周期性问题,另一方面是函数的凸性。在高中数学教材中,探讨函数的周期性问题需要结合三角函数的性质,学生对具体的周期性函数,如正弦函数、余弦函数等的周期性及判断比较熟悉,但当遇到表达式不明确,具有极强抽象性的函数问题时,需要学生根据已知条件,挖掘隐蔽的关系,这恰恰就是函数周期性问题的难点所在。函数的凸性是函数单调性的一种补充,它可以用来构造证明函数不等式,虽然函数的凸性属于高等数学知识,但近年来,它频频在高考试卷上出现,而教材上该知识点的内容相对较少,许多学生在面对函数凸性问题时都会感到束手无策[1]。
二、高中数学函数的解题方法
1.利用发散思维求解数学函数 在日常学习数学函数的过程中笔者发现,学生的发散思维占据着重要位置,要想切实提高高中生解决数学函数问题的能力,需要从多个角度分析数学函数问题,牢牢掌握多元化的函数解题方法。学生需要在学习数学函数知识时,需要努力培养自身的发散思维,采用“一题多解”的学习方法,从而加深学生对所学数学函数知识的了解,
例如:高中函数值域求解是高中数学函数的主要教学内容,在求解函数值域时,通常可采用四种方法,分别为:直接观察法、配方法、辨别式法以及利用函数有界性求解函数的值域。
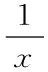
第二,配方法。在求解高中二次函数值域的过程中,最常用的解题方法为配方法,这种解题方法通过对一个式子的某一部分或者整个式子,进行恒等变形处理,使原方程式转化为完全平方式,或者是几个完全平方式的和,被广泛应用于式子的恒等变形处理过程中,可以挖掘出题目中的隐含条件,有利于学生在短时间内,准确求解函数值域。
第三,判别式法。判别式法主要应用于函数中的分式函数以及二次函数的求解过程中,也可以采用公式化简法,此种方法并非仅适用于判别不等式的形式,比如:y=b/(x2+k)这种形式的函数方程,学生可以利用不等式直接对该函数方程进行判定,而在函数方程y=bx/(x2+ex+n)中,学生首先需要对该方程式进行化简,然后利用判别式,求解此函数的值域。
第四,利用函数有界性。在高中数学函数解题方法中,此种解题方法常在求解函数值域存在困难的情况下使用,利用函数的有界性,求解函数方程的值域[2]。
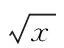
2.利用创新思维求解数学函数 在学习高中数学函数知识的过程中,仅拥有发散思维远远不够,还应具备创新思维,需要我们从多个角度分析数学函数问题,用不同的思维方式去解答函数题目,有利于培养自身的多元化思维与创新思维,在激发自身学习兴趣的同时,提高我们的数学水平。
在学习函数不等式的时候,就分别从不同的角度进行学习,觉得此种学习方法可有效提高学习效率。例如:在计算不等式2<|2x-1|<6中x的取值范围时,从三个角度对此方程式进行了解答。



由此可以看出,高中生在解答数学函数的过程中,要注重培养自身的解题思路和解题思维,建立多元化的解题思维模式,以此来提高自身的函数解题效率,锻炼学生的创新思维能力,掌握多种解题技巧,全面提高学生的数学能力。与此同时,学生在培养高中函数解题思路的过程中,要结合自身实际情况,注重引导解答数学函数题目的思维,将自身能力提升与函数知识紧密联系在一起,选择适合自己的解题方式,形成科学的思维方式,掌握科学的解题方法,以此来提高学生学习函数知识的效率,促进我们的全面发展。
总结:综上所述,高中生若想提高函数解题能力,需要培养自身的发散思维与创新思维。在学习高中数学函数知识的过程中,学生需要不断更新学习方法,逐渐形成多元化的解题思路,从多个角度分析数学函数问题,用不同的思维方式去解答函数题目,在激发学习兴趣的同时,牢牢掌握多元化的函数解题方法,提高自身的学习效率。因此,学生在学习高中函数知识的过程中,要充分考虑上述高中数学函数的解题方法,进而全面掌握函数知识。
[1]许诺.关于高中数学函数解题思路多元化的方法举例探索[J].科学大众(科学教育),2016,02:25.[2017-08-22].
[2]旷昕宇.关于高中数学函数解题思路多元化的方法举例探讨[J].科学大众(科学教育),2016,03:27.[2017-08-22].
[3]孙家正.关于高中数学函数解题思路多元化的方法举例探索[J].中国新通信,2017,1902:135.[2017-08-22].
湖南省怀化市第三中学 高三15班 418000)

