基于Kalman滤波的力矩电机直驱转台系统数字滑模控制
刘建林,施大发,罗德荣
基于Kalman滤波的力矩电机直驱转台系统数字滑模控制
刘建林1, 2,施大发2,罗德荣1
(1. 湖南大学电气与信息工程学院,湖南长沙,410082;2.湖南机电职业技术学院电气工程学院,湖南长沙,410151)
针对含有测量噪声和过程噪声的力矩电机直驱转台伺服系统,提出一种基于卡尔曼滤波器的数字滑模控制策略。首先,考虑到现有控制多采用计算机进行离散数字控制,首先将力矩电机伺服系统的数学模型进行数字离散化;其次,对离散化系统设计基于指数趋近率的软切换滑模控制器;最后,将设计的滑模控制器信号和带噪声的输出通过Kalman滤波器,得到系统最终输出信号。仿真实验结果表明:所设计的控制器对系统的噪声具有很强的鲁棒性和跟踪性能。
力矩电机;直驱转台;数字滑模;Kalman滤波器
随着数控机床向高速高精度方向发展,数控转台作为数控机床中的最重要部件,传统的由蜗轮蜗杆或齿轮副传动方式已经难以适应现有机床的高速高精度要求[1−2],这是由于蜗轮蜗杆传动,其启动和制动速度及其加速度低,且在启动、加速、反转和制动过程中存在的摩擦、弹性形变及反向间隙等会降低系统的响应能力和精度。力矩电机直驱转台直接由力矩电机通过联轴器驱动数控转台,省去了中间的传动环节,提高了系统的动态性能。然而,将力矩电机直接与数控转台相连接,外部负载、噪声等将直接通过数控转台作用于力矩电机,使其对外部的干扰尤为敏感,这在一定程度上增加了系统控制的难度[3−4]。孙宜标等[5−7]进行了系统的鲁棒控制和滑模控制研究,取得了较好的控制效果。滑模控制由于具有结构简单、易于实现等优点,在电机、机器人、飞机等领域的控制得到广泛应用[8−11]。王燕等[12]提出了一种基于趋近率的终端滑模,实现了力矩电机的精密位置跟踪。谢道成等[13]将该方法用于再入飞行器的导引律控制。席雷平等[14]针对具有不确定性的机械臂系统,提出了一种变指数趋近率的滑模控制策略。由于实际的系统均是由计算机进行数字采样控制,因此,有必要对连续的系统进行离散化,进而进行数字化设计。离散滑模控制已被广泛应用于四旋翼飞行器、风机、混沌系统、伺服系统等的控制[15−18]。HUN等[19]采用离散滑模控制实现了直流电机的变采样时间速度跟踪控制。BOBAN等[20]将离散滑模控制用于异步感应电机的高精密位置跟踪控制,并设计了干扰观测器来进一步提高系统的性能。本文作者首先根据力矩电机的伺服系统数学模型,通过采样将其进行数字离散化,得到离散系统的状态空间模型;其次,根据离散滑模控制理论,设计出离散滑模控制器,针对实际的系统中存在的过程误差和测量误差,设计了Kalman滤波器;最后,通过仿真对本方案进行验证。
1 力矩电机伺服系统的离散模型
忽略磁路饱和,仅考虑基波分量时,力矩电机伺服系统在转子坐标系下的模型,采用d=0的控制方式,力矩电机的运动动态方程可表示为
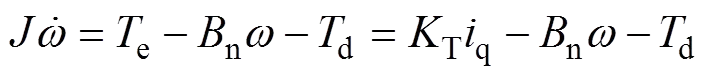
式中:为转台系统的转动惯量;n为电机的黏性摩擦因数;d为系统的扰动(包括负载扰动、摩擦及推力波动等);e为电磁转矩;T为电磁转矩系数;为电机的机械旋转角速度;q为轴电流适量;转子角位置。
对式(1)进行Laplace变换,求得对应的电流到位置的传递函数为
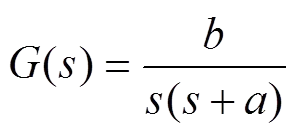
将式(2)表示为状态方程形式:
(3)
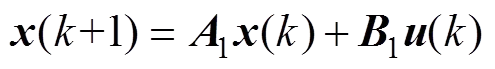
考虑系统存在的过程误差和测量误差,系统的模型可表示为:
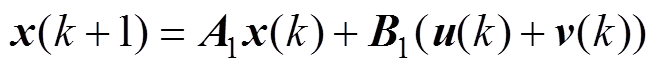
(6)
2 基于Kalman滤波器的力矩电机伺服系统数字离散滑模控制器设计
2.1 数字离散滑模控制器设计
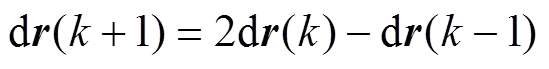
取离散滑模切换函数为
,(8)
力矩电机伺服系统数字滑模控制的目标是设计离散滑模控制(),使闭环系统(5)渐进稳定。
针对力矩电机伺服系统(5),采用式(9)所示控制率,闭环系统是渐进稳定的。
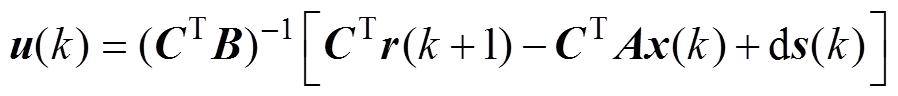
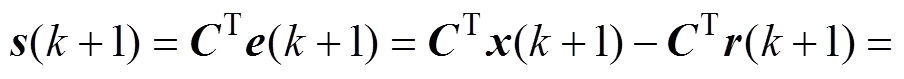
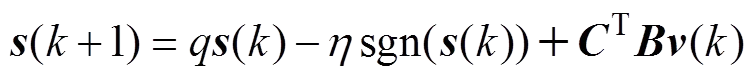
<<,<<,
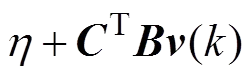
>,<0。
下面分4种情形进行分析。
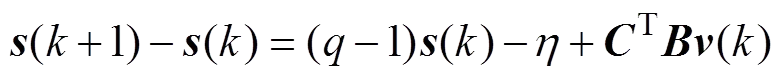
≥
>0,
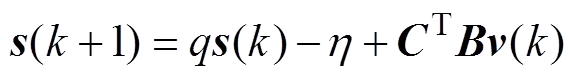
<
>
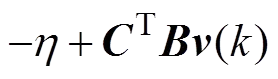
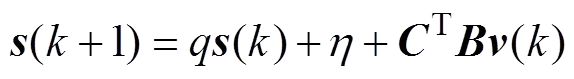
<
<,
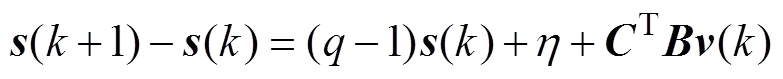
<
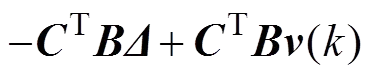
综上所述,可得:
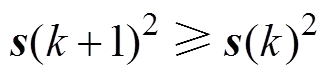
<(12)
2.2 数字滤波器设计
图1所示为包含测量误差和过程误差的系统控制结构图。
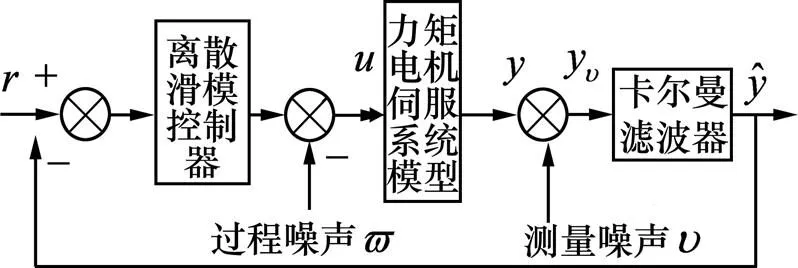
图1 含噪声的力矩电机伺服系统控制系统
由图1可知:由于系统测试中难免存在各种噪声,影响系统输出精度,因此,本文利用Kalman滤波器对输出的结果进行滤波,再将其进行反馈和输出,以提高系统性能。
针对系统(5)和(6),滤波器设计主要步骤如下。
1) 初始化方差矩阵(0),(0)和输出值0:
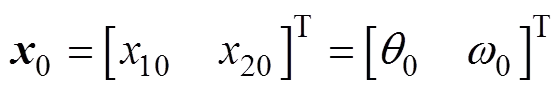
2) 根据−1时刻的(),预估时刻的,并计算误差协方差矩阵预估值:
(13)
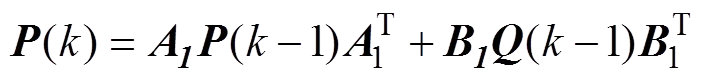
(15)
4) 预估值校正:
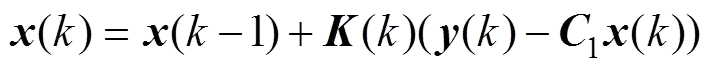
5) 误差方差矩阵校正:
(17)
3 数值仿真实验
为了验证本文所提出方案的正确性,以RM410/100力矩电机为对象,对其组成的控制系统进行仿真验证。
力矩电机的主要参数如下:额定转速N= 79 r/min;额定转矩N=856 N·m;转矩系数T= 85 N·m/A,转动惯量=5.2 kg·m2;黏性摩擦因数n= 12 N·m·s/rad;电感系数d=q=220.4 mH;电阻s=10 Ω。
根据上述电机参数,可求得其传递函数为
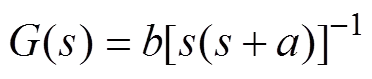
将其离散化后,可求得
,,。
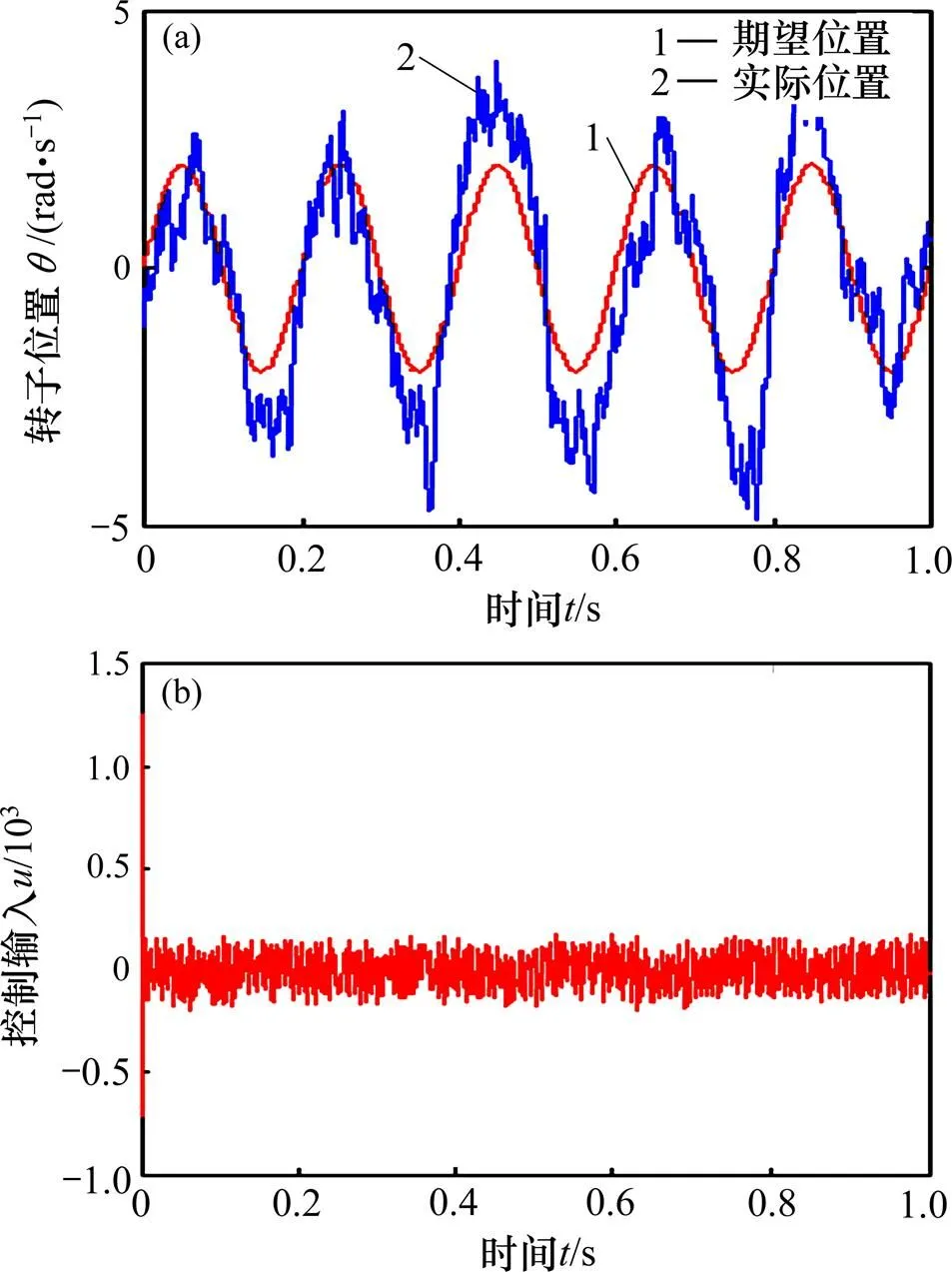
从图2可见:未进行滤波时,力矩电机直驱转台系统的输出信号能够跟踪输入转子位置信号,但输出信号存在很大的波动,不能精确地跟踪转子的指令信号,这是系统中存在各种噪声所致;另一方面,控制输入的等效电流上下波动值范围达到±200 N/A,不能达到很好的控制效果。
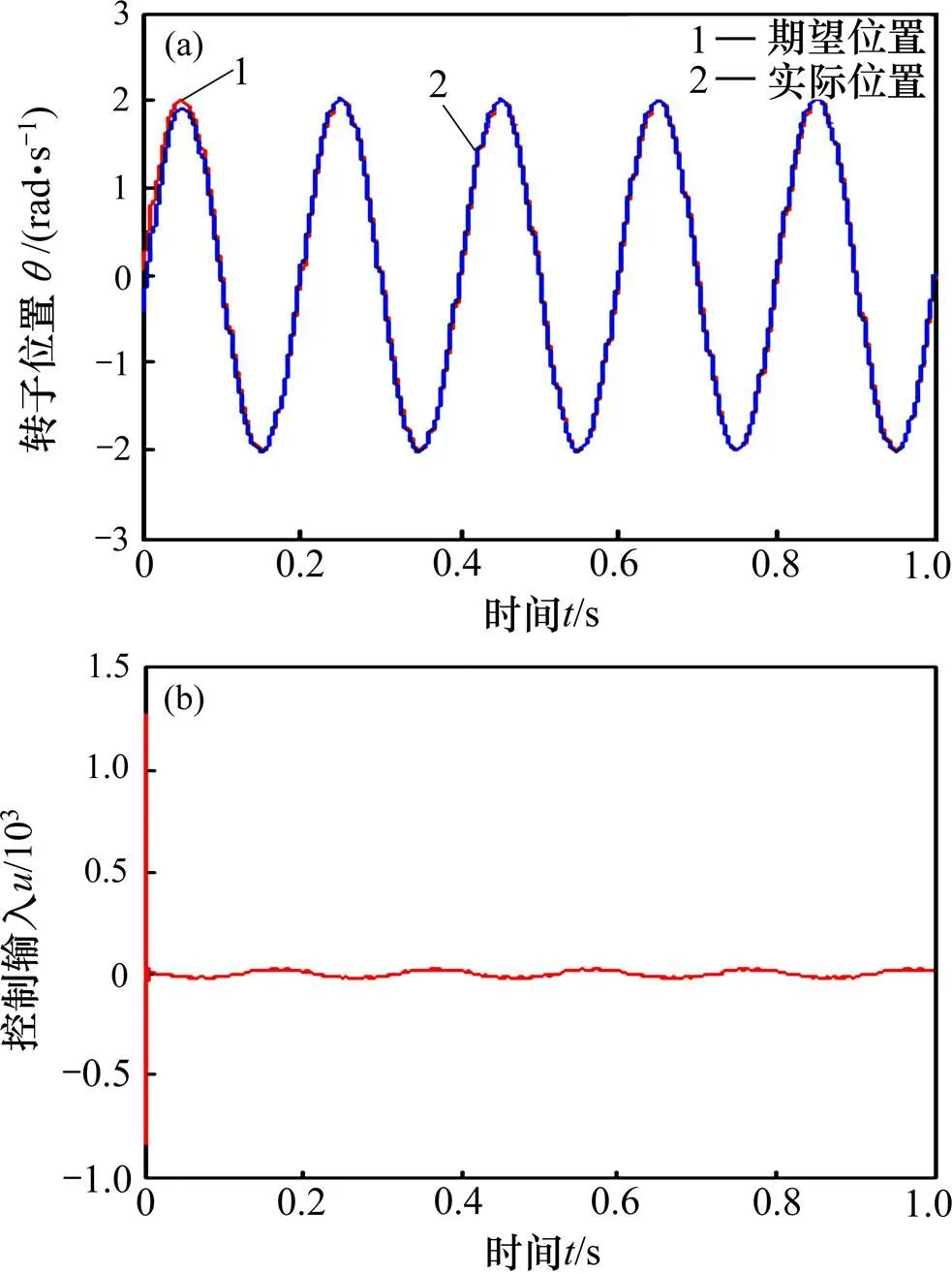
图3所示为本文提出的进行数字Kalman滤波后的响应曲线。
比较图3与图2可以看出:滤波后的转子位置很快能精确跟踪转子的位置,稳态位置跟踪误差在5%以内;控制输入的等效电流是幅值较理想的正弦波。
图4所示为加入滤波器后力矩电机直驱转台控制系统相轨迹曲线。从图4可以看出:采用本文方法其相轨迹(位置误差及其变化率的理想轨迹)能很快进入滑模面并沿滑模面趋近于零点附近,也就是说,所提出的方案控制系统能够快速稳定到期望速度,实现转子位置的快速跟踪。
2) 对外部负载的抗扰动能力。在=500(即=0.5 s)时加入d/=0.5的外部负载,力矩电机直驱转台系统的响应曲线如图5所示。
(a) 转子位置跟踪曲线;(b) 控制输入曲线
(a) 转子位置的跟踪曲线;(b) 控制输入曲线
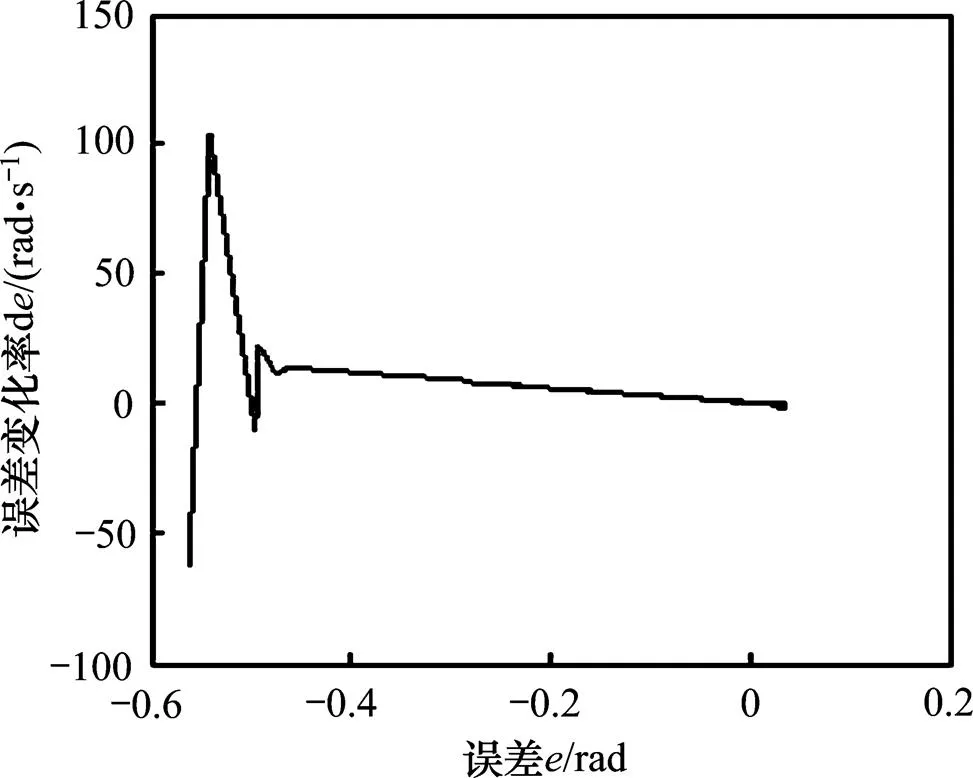
图4滤波后力矩电机直驱转台控制系统相轨迹曲线
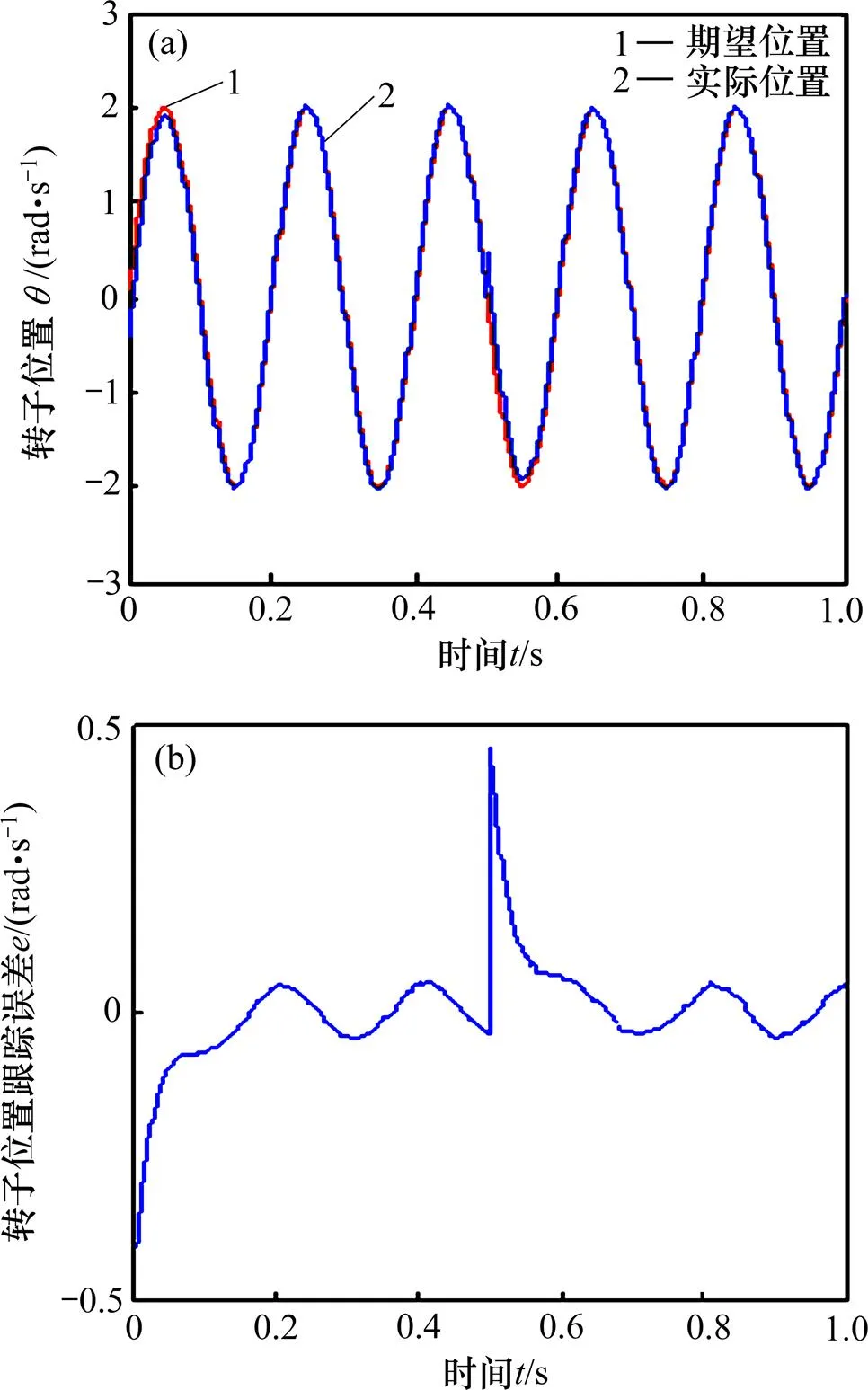
(a) 转子位置跟踪曲线;(b) 转子位置误差曲线
从图5可以看出:采用数字滑模控制时,即使在=0.5 s时有外部负载扰动,仍能够很好地跟踪转子位置,只是在突加负载时会有较大的波动,但经历0.06 s即能很快恢复其跟踪性能,具有良好的控制效果。
从图2~5可以得出:采用本文方法,通过数字Kalman滤波能够有效抑制噪声干扰对系统性能的影响,通过数字滑模可以实现对系统外部扰动的有效抑制,实现系统位置的精确跟踪。
4 结论
针对含有噪声和外部扰动的力矩电机直驱转台伺服系统,提出一种具有鲁棒性的数字离散滑模控制器。该控制器具有以下性能:
1) 能够有效地抑制各种噪声对系统位置跟踪精度的影响。
2) 能够在突变负载扰动时仍能快速实现转子位置的跟踪。
3) 设计的控制器结构简单,易于实现。
[1] 唐传胜, 戴跃洪, 孙华. 直驱转台伺服系统的优化神经网络滑模位置控制研究[J]. 机床与液压, 2012, 40(1): 13−15, 57. TANG Chuansheng, DAI Yuehong, SUN Hua. Optimal neuro-sliding mode position control for direct-drive rotary table servo system[J]. Machine Tool & Hydraulics, 2012, 40(1): 13−15, 57.
[2] 孙宜标, 金石, 王成元. 数控转台回转送进系统伺服刚度的鲁棒控制[J]. 中国机械工程, 2007, 18(16): 1966−1969, 1973. SUN Yibiao, JIN Shi, WANG Chengyuan. Robust control for servo stiffness of NC rotary table rotary feeding system[J]. China Mechanical Engineering, 2007, 18(16): 1966−1969, 1973.
[3] 叶道鑫, 洪荣晶, 吴承云. 力矩电机直驱静压数控转台动态性能研究[J]. 组合机床与自动化加工技术, 2015, 56(10): 15−18. YE Daoxin, HONG Rongjing, WU Chengyun. Dynamic performance research for torque motor direct drive hydrostatic NC rotary table[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2015, 56(10): 15−18.
[4] 赵宏安, 张然, 董建军, 等. 直驱转台技术在立式车铣复合加工中心上的应用[J]. 制造技术与机床, 2011, 61(4): 37−39. ZHAO Hongan, ZHANG Ran, DONG Jianjun, et al. The application research of direct drive rotary table in vertical turning-milling compound machining center[J]. Manufacturing Technology & Machine Tool, 2011, 61(4): 37−39.
[5] 孙宜标, 金石, 王成元. 基于线性矩阵不等式的环形永磁力矩电机的H2/H∞静态输出反馈控制[J]. 中国电机工程学报, 2007, 27(15): 8−14. SUN Yibiao, JIN Shi, WANG Chengyuan. LMI-based H2/H∞output feedback control for ring permanent magnet torque motor[J]. Proceedings of The Chinese Society for Electrical Engineering, 2007, 27(15): 8−14.
[6] 孙宜标, 金石, 王成元. 数控转台直接驱动回转送进系统的鲁棒2自由度∞控制[J]. 机械工程学报, 2008, 44(2): 152−156. SUN Yibiao, JIN Shi, WANG Chengyuan. Robust 2 degree-of-freedom∞control for NC rotary table direct drive rotary feeding system[J]. Chinese Journal of Mechanical Engineering, 2008, 44(2): 152−156.
[7] 孙宜标, 孙晓雨, 夏加宽, 等. 基于奇异摄动环形永磁力矩电机的二阶滑模控制[J]. 沈阳工业大学学报, 2008, 30(2): 148−153. SUN Yibiao, SUN Xiaoyu, XIA Jiakuan, et al. Second order sliding mode control of ring permanent magnet torque motor based on singular perturbation[J]. Journal of Shenyang University of Technology, 2008, 30(2): 148−153.
[8] 薛昭武, 张海光, 翁俊峰. 交流伺服系统的智能滑模控制[J]. 福州大学学报(自然科学版), 2004, 32(5): 572−577. XUE Zhaowu, ZHANG Haiguang, WENG Junfeng. Intelligent sliding-mode controller in PMSM AC servo system[J]. Journal of Fuzhou University (Natural Science Edition), 2004, 32(5): 572−577.
[9] 陈硕, 林小武. 基于非奇异终端滑模的永磁同步电机无速度传感器直接转矩控制[J]. 福州大学学报(自然科学版), 2013, 41(5): 875−881. CHEN Shuo, LIN Xiaowu. Research on sensorless DTC of PMSM based on nonsingular terminal-sliding-mode[J]. Journal of Fuzhou University (Natural Science Edition), 2013, 41(5): 875−881.
[10] ROSSOMANDO F G, SORIA C M. Adaptive neural sliding mode control in discrete time for a SCARA robot arm[J]. IEEE Latin America Transactions, 2016, 14(6): 2556−2564.
[11] WANG F J, LIANG C M, TIAN Y L, et al. Design and control of a compliant microgripper with a large amplification ratio for high-speed micro manipulation[J]. IEEE/ASME Transaction on Mechatronics, 2016, 21(3): 1262−1271.
[12] 王燕, 芦逸云, 葛运旺. 基于趋近率的力矩电机终端滑模轨迹跟踪控制[J]. 华中科技大学学报, 2013, 41(4): 83−87. WANG Yan, LU Yiyun, GE Yunwang. Terminal sliding mode control of trajectory tracking of torque motors using reaching law[J]. Journal of Huazhong University of Science and Technology (Nature Science Edition), 2013, 41(4): 83−87.
[13] 谢道成, 胡亚忠, 张宏强. 带末端角度和速度约束的再入飞行器滑模变结构导引律[J]. 电光与控制, 2014, 21(11): 46−50. XIE Daocheng, HU Yazhong, ZHANG Hongqiang. A sliding mode guidance law for reentry vehhicles with impact angle and terminal velocity constraints[J]. Electronics Optics & Control, 2014, 21(11): 46−50.
[14] 席雷平, 陈自力, 李小民. 机械臂变指数趋近率滑模控制律设计[J]. 电光与控制, 2012, 19(4): 47−49, 54. XI Leiping, CHEN Zili, LI Xiaomin. Design of a sliding mode control scheme based on improved exponent trending law for robotic manipulators[J]. Electronics Optics & Control, 2012, 19(4): 47−49, 54.
[15] XIONG Jingjing, ZHANG Guobao. Discrete-time sliding mode control for a quadrotor UAV[J]. International Journal for Light and Electron Optics, 2016, 49(17): 332−337.
[16] TORCHANI B, SELLAMI A, GARCIA G. Variable speed wind turbine control by discrete-time sliding mode approach[J]. ISA Transactions, 2016, 62: 81−86.
[17] YANA J J, CHENA C Y, TSAI J S. Hybrid chaos control of continuous unified chaotic systems using discrete rippling sliding mode control[J]. Nonlinear Analysis: Hybrid Systems, 2016, 22(6): 276−283.
[18] BARATIERI C L, PINHEIRO H. New variable gain super-twisting sliding mode observer for sensorless vector control of nonsinusoidal back-EMF PMSM[J]. Control Engineering Practice, 2016, 52: 59−69.
[19] HUN C W, LIN C T, LIU C W, YEN J Y. A variable-sampling controller for brushless DC motor drives with low-resolution position sensors[J]. IEEE Transaction on Industrial Electronics, 2007, 54(5): 2846−2852.
[20] BOBAN V, BRANISLAVA P D, CEDOMIR M. High- performance position control of induction motor using discrete- time sliding-mode control[J]. IEEE Transactions on Industrial Electronics, 2008, 55(11): 3089−3817.
(编辑 陈灿华)
Digital sliding mode control of direct drive rotary table servo systems of torque motor based on Kalman filter
LIU Jianlin1, 2, SHI Dafa2, LUO Derong1
(1. College of Electrical and Information Engineering, Hunan University, Changsha 410082, China;2. Department of Electrical Engineering, Hunan Mechanical & Electrical Polytechnic, Changsha 410151, China)
Focused on the problems of measurement noise and process noise existing in the servo system of torque motor direct drive rotary table, Kalman filter based digital sliding mode control strategy was presented. Firstly, considering that computers were used in most of the control method for servo systems, the mathematical model of the torque motor servo system was discretized. Then, soft switch sliding mode control with exponential reaching law was designed. Finally, the output signals of the designed controller and system with noises were passed through the Kalman filter, and the final output signal was obtained. The simulation results show that the proposed system with the proposed method has strong robustness with noise and high tracking performance.
torque motor; direct drive rotary table; digital sliding mode; Kalman filter
10.11817/j.issn.1672-7207.2017.09.016
TM301.2
A
1672−7207(2017)09−2370−06
2016−10−07;
2016−12−26
国家自然科学基金资助项目(51577052);湖南省教育厅科技项目(16C0571) (Project(51577052) supported by the National Natural Science Foundation of China; Project(16C0571) supported by Education Department of Science and Technology Project of Hunan Province)
刘建林,副教授,从事电机技术、智能控制技术研究;E-mail: tikolin@126.com

