残差灰色预测模型在汽车保险杆涂层自然老化研究中的应用

王剑，潘晓涛，张晓东，曾文波，揭敢新,*，钟少基

（1.广东工业大学材料与能源学院，广东 广州 510006；2.中国电器科学研究院有限公司工业产品环境适应性国家重点实验室，广东 广州 510663）

残差灰色预测模型在汽车保险杆涂层自然老化研究中的应用

王剑1,2，潘晓涛1，张晓东2，曾文波2，揭敢新2,*，钟少基1

（1.广东工业大学材料与能源学院，广东 广州 510006；2.中国电器科学研究院有限公司工业产品环境适应性国家重点实验室，广东 广州 510663）

构建了残差灰色预测模型，对湿热环境自然曝晒下汽车保险杆涂层的色差变化情况进行预测。结果表明：该模型的色差模拟值与实测值的最大相对误差为4.1400%，优于灰色GM(1,1)预测模型的预测结果(最大相对误差为17.0769%)，可以用于汽车保险杠涂层老化行为的预测。

汽车保险杠；涂层；湿热环境；自然老化；预测；灰色理论；残差；模拟

Abstract:A grey residual error model was established for predicting the variation of color difference of automobile bumper coating exposed in damp heat environment.The results showed that the maximum relative error of its simulation value with respect to the measured value is 4.1400%, which is better than that (17.0769%) of the grey GM(1,1) prediction model.It is proved that the grey residual error model can be used to predict the aging behavior of automobile bumper coating.

Keywords:automobile bumper; coating; damp heat environment; natural aging; prediction; grey theory; residual error;modeling

First-author’s address:School of Materials and Energy, Guangdong University of Technology, Guangzhou 510006, China

汽车涂层具有防护和装饰双重效果，耐老化是其重要的性能之一。传统上是通过自然曝晒老化试验来考察汽车涂层的耐老化性能，但是该试验花费时间很长，至少需要一年，有的甚至长达数十年[1-2]，比较难跟上材料的更新速度。以这种方法来确定汽车涂层使用寿命的效率太低，而加速老化试验又无法完全模拟汽车涂层的实际使用环境。近年来已有不少学者利用数学模型对涂层或其他材料的老化行为进行研究[3-6]。

灰色系统理论由邓聚龙教授创立以来，迅速受到相关领域学者的高度重视，并且得到国际学术界的充分肯定。传统灰色GM(1,1)预测模型适用于只知部分信息的不确定系统，可利用少量数据建立预测模型来确定系统未来的变化趋势[7]。但对于随机非平稳变化的系统，它的预测精度不高，阻碍了其应用发展。不少学者结合其他数学模型对灰色GM(1,1)预测模型进行研究以提高其预测精度，残差修正模型便是其中之一[8]。本文利用某车型汽车涂层自然曝晒试验的色差数据建立灰色残差预测模型，研究了其在汽车涂层自然老化行为试验中的适用性。

1 灰色模型的建立

1.1 灰色GM(1,1)预测模型

灰色 GM(1,1)预测模型通过对原始数据生成开发，提取有价值的信息，从而预测未来趋势。灰色GM(1,1)预测模型是由一个包含单变量的一阶微分方程构成的模型，其原始形式实质上是一个差分方程。建模步骤如下：

(1) 根据原始数据构建原始序列 X(0)。

(2) 对原始数据累加处理，生成一次累加(1-AGO)序列 X(1)，再根据 X(1)生成紧邻值序列 Z(1)。

(3) 计算模型参数，得到灰色GM(1,1)预测模型。

灰色GM(1,1)预测模型的灰色微分方程如式(3)所示：

灰色GM(1,1)预测模型的最小二乘估计参数列满足式(4)。

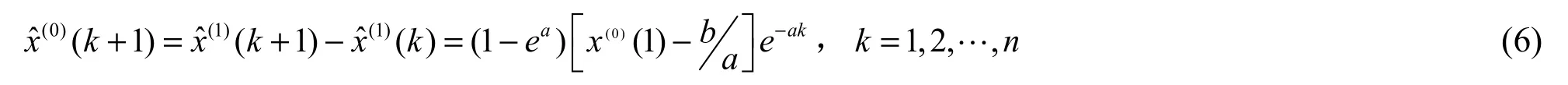
1.2 残差灰色预测模型

其中，εa和εb分别是残差灰色预测模型的发展系数和灰色作用量，其求法与灰色GM(1,1)预测模型的a、b求法类似。残差修正值通过式(10)做累减还原得到。

1.3 模型误差检验

误差检验一般采用后验差和残差检验，后验差检验针对的是残差分布，是残差统计特征的检验；残差检验是逐点检验的方法[7]。后验差检验方法主要依靠后验差比值C和小误差概率P来验证。

初始数据与模拟数据之差简称为残差ε(k)。

按式(17)计算相对误差kεΔ

表1 灰色模型的精度等级判别[10]Table 1 Precision rating of a grey model[10]

2 实验

2.1 汽车的自然曝晒试验

参照QC/T 728–2005《汽车整车大气暴露试验方法》，将某品牌汽车整车置于工业产品环境适应性国家重点实验室海南琼海湿热自然暴露试验场内进行静态暴露试验。试验车的前挡风玻璃朝向赤道方向，放置情况如图1所示。每2个月遵循GB/T 3979–2008《物体色的测量方法》，使用日本柯尼卡美能达公司的CM-2300D型分光测色计测量前保险杠涂层的色差，使用D65标准光源，10°观测角。每次测量随机选5个点，取平均值。试验时间为2年[1]。

图1 自然环境下整车曝晒试验照片Figure 1 Photo showing the exposure test of a whole vehicle under natural environment

2.2 建模

试验车曝晒1年后，涂层受到太阳光辐射、热、湿气、污染物等环境因素影响而逐渐老化，使用性能降低。汽车前保险杆涂层的色差随时间变化的情况见表2。以涂层色差变化数据进行灰色GM(1,1)预测模型建模。由表2可知原始序列 X(0)为{0.28，0.48，0.39，0.50，0.56，0.68}，根据式(1)对原始序列进行一次累加得到 X(1)为{0.2000，0.6800，1.0700，1.5700，2.1300，0.8100}，根据式(2)对 X(1)进行紧邻值处理得到 Z(1)为{0.4400，0.8750，1.3200，1.8500，2.4700}。根据 X(0)和Z(1)序列可以得到Y和B中具体的数值，再由公式(4)得到 aˆ= [a,b]T=[0.1167,0.3597]T，即a = 0.1167，b = 0.3597。根据式(5)和式(6)进一步得到灰色GM(1,1)预测模型的微分方程的时间响应函数的还原值函数如式(18)所示。

表2 2种模型预测的汽车前保险杠涂层色差Table 2 Color differences of automobile bumper coating predicted by two models, respectively

灰色GM(1,1)预测模型对汽车前保险杠涂层色差预测结果也列于表2。可见模拟值和实测值的相对误差比较大，最大相对误差为17.0769%。这说明该模型不够准确。因此建立残差灰色预测模型予以修正。取表2中灰色GM(1,1)预测模型残差序列(k )，即{0.0737，−0.0666，−0.0131，−0.0165，0.0321}，根据式(8)对序列进行非负处理，得ε(0)(k)，即{0.2069，0.0666，0.1201，0.1167，0.1653}，据此得到残差灰色预测模型的残差修正模型为：

经计算，灰色GM(1,1)预测模型和残差灰色预测模型对保险杠涂层色差预测对比情况见表2。两者的精度对照情况见表3。灰色GM(1,1)与残差灰色预测模型的精度均为一级，但后者的预测误差比前者的预测误差小，说明后者预测的结果更加贴合实际情况。

表3 2种模型的精度对照Table 3 Comparison between precision of the two models

利用残差灰色预测模型对涂层的色差进行第二年的预测，k取 6、7、8、9、10和 11，分别得到第14、16、18、20、22和24月的预测值，并与第二年试验测得的涂层色差比较，结果见表4。

表4 用残差灰色模型所得汽车保险杠涂层色差预测值和实测值的对比Table 4 Comparison between the color difference values of an automobile bumper coating predicted by grey residual error model and those measured actually

可见残差灰色预测模型对涂层的色差预测与实际情况比较吻合。综合GB/T 1766–2008《色漆和清漆涂层老化的评级方法》和各车企的标准，色差值大于1.5判定为很轻微失色，小于1.5判定为无失色。色差预测值和测量值在第22月后都超过了1.5，属于很轻微失色的情况。

3 结论

自然环境下，涂层老化行为变化情况受较多的环境因素影响，很难通过实际试验来确定。针对这一状况，根据灰色理论建立了灰色GM(1,1)预测模型和残差灰色预测模型对汽车保险杠涂层在海南琼海湿热自然环境下老化行为的变化进行预测。对于随机非稳定序列，由于残差灰色模型对序列首端附近的误差进行了修正，预测结果相对于灰色GM(1,1)预测模型的预测结果更符合实际情况，精度等级更高，为汽车保险杠涂层老化的研究提供一条新的途径。

[1]马坚, 揭敢新, 刘强, 等.汽车气候老化应用技术[M].广州: 华南理工大学出版社, 2013: 9-10.

[2]张晓东, 王俊, 揭敢新, 等.干热环境下的汽车耐候性试验结果分析[J].汽车工艺与材料, 2015 (10): 36-38.

[3]尚建丽, 王健.GM(1,1)模型在外饰面涂层耐久性预测中的应用[J].涂料工业, 2010, 40 (8): 13-15.

[4]黄伟, 仇君.塑料自然老化力学性能的灰色预测[J].广西大学学报(自然科学版), 2001, 26 (4): 275-277, 282.

[5]ARNAUD R, ROMAIN L, STÉPHANE C, et al.Modeling of hydrothermal aging of short flax fiber reinforced composites [J].Composites Part A: Applied Science and Manufacturing, 2016, 90: 559-566.

[6]MARINE J, RAFAEL G, DANIEL H, et al.PEMFC aging modeling for prognostics and health assessment [J].IFAC-PapersOnLine, 2015, 48 (21): 790-795.

[7]邓聚龙.灰色系统基本方法[M].2版.武汉: 华中科技大学出版社, 2005: 209-211.

[8]刘思峰, 党耀国, 方志耕, 等.灰色系统理论及其应用[M].3版.北京: 科学出版社, 2004: 447-448.

[9]张天云, 陈奎, 胡玉霞, 等.残差灰色预测模型在塑料老化行为预测中的应用[J].现代化工, 2013, 33 (5): 119-121, 123.

[10]王鹏, 黄显峰, 崔延松.灰色残差模型在城市工业需水量预测中的运用[J].机械制造与自动化, 2014, 43 (5): 135-138.

[ 编辑：杜娟娟 ]

《电镀与涂饰》杂志微信号(ddyts1982)实施签到积分奖励计划

点击自定义菜单“行业互动→签到奖励”即可进入会员中心进行签到，签到前需先绑定会员。

微信自动绑定仅限于首次关注，非首次关注需手动绑定会员。

积分兑换计划已经开始，微信签到积分和表面处理领航网(www.sfceo.net)积分已经合并。

网站兑换网址：http://www.sfceo.net/gift/。

微信签到及兑换方式如下：

Application of grey residual error prediction model in study of natural aging of automobile bumper coating

WANG Jian, PAN Xiao-tao, ZHANG Xiao-dong, ZENG Wen-bo, JIE Gan-xin*, ZHONG Shao-ji

TQ638

B

1004 – 227X (2017) 18 – 1000 – 05

2017–05–18

2017–08–26

广州市科学研究专项支持项目（201504010020）。

王剑（1990–），男，广西玉林人，在读硕士研究生，工程师，研究方向为工业产品环境。

揭敢新，教授级高级工程师，(E-mail) 871540963@qq.com。

10.19289/j.1004-227x.2017.18.010