地铁车站对临近场地地震反应谱影响分析

张亚辉，宋玉香，郭唯伟，刘 勇

（石家庄铁道大学，河北 石家庄 050043）

地铁车站对临近场地地震反应谱影响分析

张亚辉，宋玉香，郭唯伟，刘 勇

（石家庄铁道大学，河北 石家庄 050043）

考虑土—结构相互作用影响，分析在不同的地震波作用下不同结构形式地铁车站对临近场地地震动响应的影响规律。经过两次反演得到地铁车站所在深度的EL-Centro波，将此波形与生成的人工波分别作用于自由场地与包含地铁车站的两种地层结构，将得到的场地反应谱特性与自由场地表反应谱进行对比。由对比结果可知：在短周期部分地铁车站的存在使得地表加速度反应谱谱值变大，而在长周期部分，地表加速度反应谱谱值变化相对而言较小，即地铁车站的存在对地表加速度反应谱的长周期部分基本不影响；在不同地震波作用下，不同地铁车站结构对临近场地土反应谱的变化影响度因子曲线均呈倒“S”型，有唯一拐点；地铁车站结构的跨度与高度越大，其对周围场地土反应谱带来的影响越大。

土—结构相互原理；反应谱；动力响应；频谱特性

0 引言

目前国内外学者对于土—地下结构动力相互作用体系[1]的地震动反应做了很多分析和研究讨论，此类文献也较多，而对于地铁车站等地下工程开挖后对场地土层以及临近建筑物的地震反应的影响的研究还比较少。对该问题的研究，目前主要采用解析法和数值法。解析法在问题本质分析方面有着重要的作用，但是由于波动问题的复杂性，解析法仅可适用于一些简单的工况，且多针对于平面SH型波，如半圆形河谷场地的散射椭圆孔对SH波的散射及圆弧形凹陷地形等特殊情况[2]，而对于平面P波和SV波入射情况由于它们在散射时的波型转换，比SH波要复杂得多，要获得解析解有些困难。梁建文等[3]采用波函数展开法，给出了平面P波和SV波人射下均匀半空间中洞室群对地面运动影响问题的一个级数解答，对于均匀地质的理想情况提供了参考。地铁地下结构地震反应分析属于典型的土—结构动力相互作用问题，场地土条件对地铁结构的抗震性能有着重要的影响，地下结构对自由场地地震响应分析是反应谱理论领域重要的研究内容。

本文考虑土—结构相互作用影响，通过输入不同的地震波，分析不同结构形式地铁车站对临近场地地震动响应的影响规律。

1 模型建立

1.1 土体破坏准则

1952年Drucker和Prager首先把不考虑中间主应力2σ影响的Coulomb屈服准则与不考虑净水压力影响的Mises准则联系在一起，提出广义理想塑性模型，即D-P模型。D-P模型的屈服面方程为：

D-P屈服函数所表示的屈服面在π平面上是一个圆，更适合数值计算。由于D-P准则常作为近似计算，因此该模型被广泛应用于岩土工程的土体计算中。

在分析软件ANSYS中能用于岩土材料的模型只有D-P模型。

D-P模型（Drucker-Prager准则）是理想弹塑性模型，理想弹塑性即应力达到屈服极限以后，应力不再增大，但是应变会一直增大。

ANSYS中设定D-P模型需要输入三个参数：粘聚力、内摩擦角、计算摩擦角，其中的膨胀角是用来控制体积膨胀的大小的。在岩土工程中，一般密实的砂土和超强固结土在发生剪切的时候由于颗粒的重新排列导致出现了体积膨胀；而一般的砂土或者正常固结的土体，只会发生剪缩。

1.2 计算模型

选取典型的单层双跨地铁车站为对象进行分析。为简化计算，在ANSYS中设定岩土体为弹塑性模型，将实际的三维问题简化为二维平面应变问题来计算。车站结构混凝土为C35，主筋为Ⅱ级钢筋，箍筋为Ⅰ级钢筋。利用大型有限元分析软件ANSYS中的Plane42单元类型来模拟土体，采用Beam3单元模拟主体衬砌结构，结构与土体接触面采用接触单元。通过命令“TB,DP,1”将土体单元类型1定义为D-P材料模型，“TBDATA,,20e3,31,29”分别定义土体的粘聚力20kPa、内摩擦角31o、计算摩擦角29o。

土体有限元模型宽度取5倍于结构宽度，埋深取4.8m。有限元网格划分根据土体分层和计算精度需要进行划分。模型两侧边界采用粘弹性人工边界，地表自由边界，模型底部X与Y方向均施加约束。由基岩底部输入地震波，其计算模型如图1所示，土—结构模型网格化分如图2所示。

图1 计算模型图Fig.1 Calculation model

图2 计算模型以及监测控制点编号Fig.2 Calculation model & number of the control points

车站所处地区场地土采用北京地区实测场地土，土层参数如表1所示。

1.3 地震波的选择与输入

选取EL-Centro以及人工生成波（峰值是36cm/s2）。在计算中为了缩短计算时间，同时达到说明问题的效果，对各波形选取了加速度值较大的时段：0～16s，并且对地震波形进行基线修正，修正后可得到如下图3-4所示的地震波。由于由基岩底部输入地震波，对地表一些点的加速度变化进行监测，以反映地铁车站存在对场地地表地震动的影响。假定地下车站的中柱正上方地表处为原点，各研究控制点编号如图2所示。选取离原点水平距离为10m、20m、30m和40m处的点为对象进行分析。

由于EL地震波记录的是地震地面运动加速度，而在实际工程中，地震波是由基岩位置处传播到地面而后作用于建筑结构。加之基岩的深度不是一成不变的，不同深度基岩采用相同的基岩地震加速度曲线也是不合理的。

一般的，地震动的输入是将地震波作用到基岩上，但场地基岩埋深也许会非常深，数值模型不可能取到基岩面，所以反演过程应该是将地表记录波反演到基岩深度处，然后再将基岩深度处得到的反演波继续反演到数值模型底部的地层深度。

通过有限元法经两次反演得到的EL地震波加速度时程曲线如图5所示。

表1 两套仪器月均值数据

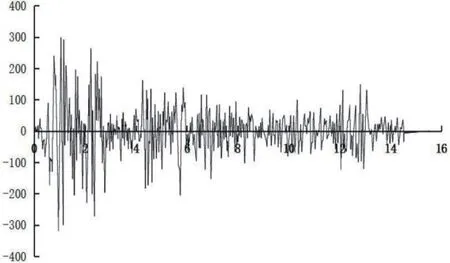
图3 EL-centro波加速度时程Fig.3 EL-centro wave acceleration curve

图4 人工生成地震波加速度时程Fig.4 Artificial wave acceleration curve

图5 反演后EL地震波加速度时程Fig.5 EL-Wave acceleration curve after inversion

2 场地地震反应谱

2.1 加速度以及反应谱变化

图6 EL-centro波作用下各测点β谱曲线Fig.6 β-spectrum curve under the action El-centro wave

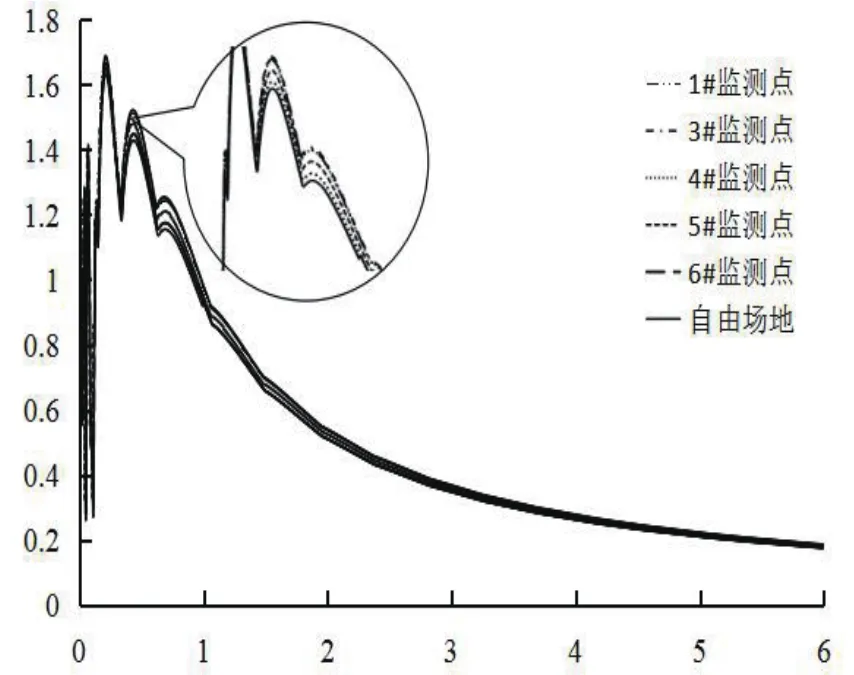
图7 人工波作用下各测点β谱曲线Fig7β-spectrum curve under the action artificial wave

由图6—7可知：在地震波作用下，地表加速度反应谱谱值与自由场相比均略有增大，离中心点越近，增幅越大，在距离中心点40m处的6#测点位置，反应谱几乎与自由场反应谱重合，即此处已经不再受地下结构的影响。在0.5～1s周期内，6个测点处的反应谱与自由场反应谱相差较大，随着周期的拉长，可以看出1s之后反应谱基本上与自由场反应谱重合。这说明，地下结构在短周期范围内对自由场地反应谱影响较大，长周期几乎没有影响。而对于加速度峰值大的EL-centro波作用下得到的反应谱幅值明显大于人工波作用下的反应谱幅值，而且引起的地表反应谱变化也较人工波条件下的明显。

地表各点峰值加速度和自由场地峰值如表2所示。场地反应谱的影响程度（存在地下结构与自由场地反应谱幅值的比值）如表3所示。

表2 地面各点峰值加速度以及变化幅值表

表3 地面各点反应谱影响度

由表2—3可知，地铁车站对场地地表加速度反应峰值影响非常明显。随着与车站中心上方地表距离的减小，地表加速度反应峰值与自由场地相应位置的值相比越来越小。洞顶正上方（原点处）的加速度反应峰值与自由场对应值相比，减小幅度为：当El-centro波激励时约为28.4%；当人工波激励时约为22.1%。

2.2 影响度因子曲线

（1）不同地震波形式影响度因子曲线

通过输入加利福尼亚大学数据处理中心的地震记录数据库管理系统中的53条地震波，定量分析地铁车站结构的存在对场地反应谱的变化影响度因子的变化规律。以1#测点为原点，离1#测点距离为横轴，影响度因子η为纵轴，得到影响度因子变化如图8所示。

由图8可以看出，影响度因子随着距离的增大逐渐向1逼近，将点连成曲线后这些曲线都有共同特征：曲线均呈倒“S”型，有唯一拐点，且拐点位置均在5～6m范围内；曲线幅值在1.2～1.35之间变化，幅值大小与地震波的频谱特性有关。将图8中的η进行平均处理得到图9中的曲线，曲线的最大值为1.328。

图8 地震波激励下影响度因子平均曲线图Fig.8 Average curve of the effect factors on seismic excitation

图9 影响度因子计算值与实测值曲线对比图Fig.9 Compared curve graph of effect factor calculated value and the measured

对曲线进行拟合，拟合曲线与实际值曲线如图9所示，得到η-r的相关方程：

函数中的绝对值是为了强调左右两侧的对称性而设的。

（2）不同结构形式车站影响因子曲线

为了分析不同结构形式对影响度因子的影响规律，选取双层双跨、双层三跨、三层三跨结构进行分析，各结构的尺寸如表4所示。

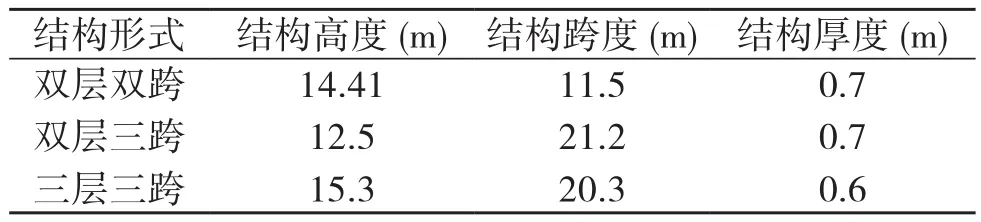
表4 结构尺寸

通过改变结构形式，对模型输入地震波，分析场地反应谱影响度因子的变化规律，并进行拟合，各结构形式车站对应的η-r方程分别为：

双层双跨时：

双层三跨时：

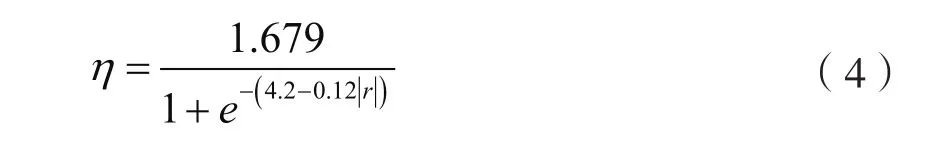
三层三跨时：

由式（2）—（5）可知，各结构形式对场地土反应谱曲线均呈倒“S”型，有唯一一个拐点；跨度与高度越大，则结构对周围场地土反应谱带来的影响越大。

3 结论

考虑土—结构相互作用影响，对典型的单层双跨地铁车站，建立土—地下车站结构模型，分析地铁车站对临近场地地震动响应的影响规律，通过分析得到的主要结论：

（1）地铁车站对临近场地地表加速度的影响程度取决于与输入地震波的频谱特性。在EL-Centro波和人工波分别作用下，与自由场地表反应谱相比，在短周期部分，地铁车站的存在使得地表加速度反应谱谱值变大，在长周期部分使得地表加速度反应谱谱值变化较小。

（2）地铁车站结构对临近场地地震动的影响，与输入的地震波形式和结构形式有密切关系。通过输入多条地震波、选取不同的结构形式，分析地铁车站结构的存在对场地反应谱的变化影响度因子的变化规律可知，各结构形式、在不同地震波作用下对临近场地土反应谱曲线均呈倒“S”型，有唯一一个拐点；跨度与高度越大，则结构对周围场地土反应谱带来的影响越大。

（3）对于地铁车站埋深的对自由场地震动响应影响规律有待进一步深入研究。

[1] 陈国兴, 庄海洋, 徐烨. 软弱地基浅埋隧洞对场地设计地展动的影响[J]. 岩土工程学报，2004，（6） : 739-744.

[2] 林利民, 陈健云. 软土中浅埋地铁车站结构的抗震性能分析[J]. 防灾减灾工程学报， 2006. 26，（3）：268-273.

[3] Wolf 1. Soil-structure Interaction Analysis in Time Domain[M].Prenthall, 1987.

[4] Trifunac M D. Scattering of plane SH waves by a semiylindrical canyon[J]. Earthquake Engineering and Structural Dynamics，1973，1：267-281.

[5] 陈志刚, 刘殿魁. 椭回孔对SH波散射的远场解[J]. 哈尔滨工程大学学报，2003，24 （3） : 334-338.

[6] 袁晓铭, 廖振鹏. 圆弧形凹陷地形对平面SH波散射问题的级数解答[J]. 地震工程与工程振动，1993，13（2）: 1-11.

[7] 蒋楚生, 李庆海, 曹新文. 高烈度地震区高路堤桩板墙的动力响应研究[J]. 铁道工程学，2015，32 （3）.

[8] Lee V W, Karl J. Diffraction of SV Waves by Underground,circular, cylindrical cavities[J]. soil Dynamics and Earthquake Engineering, 1992, 11: 445-56.

[9] Davis C A, Lee V W , Bardet J P. Transverse response of underground cavities to incident SV waves[J]. Earth quake Engineering and Structural Dynamics，2001，30（3）：383-10.

Abstract:Considering the influence of soil structure interaction, the ground motion responsein different seismic waves and different structure influence of subway station was analysed. And the influence of surface acceleration was determined by the frequency spectrum characteristics of the input seismic waves.Compared to in El-Centro wave and artificial wave respectively under the action, and the free field surface reaction spectrum, in a short period, some subway station made of ground surface acceleration response spectrum value becomes larger,and in the long period, the surface acceleration response spectrum value were almost same.Under the different seismic waves and different structure of subway station near the ground response spectrum changes influence degree coefficient curve was inverted "S" type, with only a turning point; and the larger the span and height , the more influencewhich structure of surrounding soil to site response spectrum.

Key words：soil structure interaction; response spectrum; dynamic response; spectral characteristics

Influence Analysis of the Subway Station to the Site Based on the Earthquake Response Spectrum Effect

ZHANG Ya-hui，SONG Yu-xiang，GUO Wei-wei，LIU Yong
（School of Civil Engineering, Shijiazhuang Tiedao University, Hebei Shijiazhuang 050043，China）

P315.9；U452.21

A

10.13693/j.cnki.cn21-1573.2017.03.08

1674-8565（2017）03-0043-06

铁道部科技研究开发项目（2012G014-D）；河北省高等学校科学研究项目（ZH2012037）

2017-02-05

2017-04-16

张亚辉(1989-)，男，山西省长治市人，毕业于石家庄铁道大学，硕士，助理工程师，现主要从事地下工程抗震等方面的教学和科研工作。E-mail：zhangyahui19891020@163.com