基于双匀速轨迹的自动泊车路径规划研究

李 攀,黄 江,杨 浩,韩中海

(重庆理工大学 车辆工程学院，重庆 400054)

基于双匀速轨迹的自动泊车路径规划研究

李 攀,黄 江,杨 浩,韩中海

(重庆理工大学 车辆工程学院，重庆 400054)

针对自动泊车过程中由于路径曲率不连续而常常出现的停车原地转向的问题，提出了一种基于车辆速度和方向盘转动角速度的泊车路径生成方法。分析了在车速和方向盘转速为恒值时的车辆轨迹特点即“双匀速”轨迹特点。引入了“过渡半径”和“切入半径”的概念，将双圆弧泊车路径与“双匀速”轨迹有机地结合起来，使泊车路径生成算法以及避障算法更为简便，泊车路径的相关参数以及泊车可行域都可以用车辆速度、方向盘转动角速度和车身几何尺寸计算得到。基于预瞄理论建立倒车驾驶员模型，在Carsim里对生成的“双匀速”泊车路径进行可行性验证，结果显示：这条由车辆“双匀速”轨迹计算得到的路径在车辆非匀速泊车过程中同样有较好效果。由此可知：基于“双匀速”的泊车路径生成方法有效地解决了泊车过程中的避障问题，同时满足了路径曲率连续性的要求，从而避免了泊车过程中停车转向的问题。

汽车工程；双匀速泊车路径；避障；路径规划；自动泊车

Abstract: In order to solve the problem of shutting down to steer the wheel in parking process because of the discontinuity of path curvature, this paper proposed a path planning algorithm based on vehicle speed and steering wheel angular velocity. The characteristics of vehicle trajectory are analyzed when the vehicle speed and steering wheel speed are constant, that is, the characteristics of the “double constant velocity” trajectory. It combines the double circular trajectory with the double constant speed trajectory by introducing the concept of “transition radius” and “tangency radius”, makes path planning algorithm and collision-free algorithm more convenient. The parameters of the parking path and the feasible parking area can be calculated by the vehicle speed, the steering wheel angular speed and the body geometry. The reversing driver model was built on preview theory. The double constant speed trajectory was verified in Carsim by reversing driver model. Simulation results show good performance in the verification of double constant speed trajectory under non-uniform vehicle speed case. It is proved that the approach proposed can find a collision-free path and meet the key point of continuous trajectory curvature, so the problem of shutting down to steer the wheel in parking process is avoided.

Keywords: automotive engineering; double constant speed trajectory; collision-free; path planning; automatic parking

近年来，随着智能驾驶技术的不断发展，作为智能驾驶技术的重要组成部分——自动泊车系统(auto-parking system)也得到了汽车行业的关注。另外，由于城市汽车保有量急剧增加，停车空间越来越小，这样对驾驶员的操作水平要求越来越高，这对于新手来说更是让人头疼的问题。这些因素促使国内外学者对自动泊车技术开展了深入研究。目前，对于泊车外部环境的探测建模技术已经比较成熟，国内外学者的研究重点主要集中于泊车路径的规划与跟踪控制上。本文主要从泊车路径规划角度进行深入研究。文献[1-2]采用了两段相切的圆弧规划路径，这种方法虽然简单易行，但是存在曲率跳变点;文献[3]提出了圆弧直线路径，但是仍未解决路径不连续的问题；文献[4]采用贝塞尔曲线来规划泊车路径，解决了泊车过程中曲率不连续的问题;文献[5-6]采用B样条曲线，在考虑多约束的情况下规划出一条连续曲率的泊车路径；文献[7]将双圆弧路径与贝塞尔曲线相结合，但是仍然存在曲率不连续点；文献[8]创新性地提出一种多圆弧泊车路径生成方法;文献[9-10]采用回旋曲线连接圆弧路径保证了路径的连续性，同时计算量也没有大量增加;文献[11-12]基于车辆参数计算出连续的多段式泊车路径，但是由于没有统一的理论造成计算量稍大。本文在以上研究成果的基础上提出一种更加全面的泊车轨迹生成方法，并对轨迹生成的影响要素进行深入分析。

1 车辆双匀速运动轨迹

泊车运动中由于车辆速度比较低，根据文献[13]，可以不计轮胎的侧向滑动以及车辆的动态响应。同时由于车辆后轮为非转向轮，即后轴的运动方向与车身运动方向相同，因此可以用车辆后轴中心点的轨迹来表示车辆泊车的轨迹。本文的泊车路径生成方法可以总结为：① 泊车轨迹是假设车辆从泊车位无碰撞地移动至预备停车位的后轴中心点行驶轨迹；② 为了简化泊车路径算法方程，假设车辆后轴中心点速度和方向盘转速均为匀速。依据车辆的几何模型和转向特性即可计算出一条较为理想的泊车轨迹，本文称之为“车辆双匀速泊车轨迹”。

以下具体讨论“车辆双匀速运动行驶轨迹”的特点。设车辆后轴中心点速度为Vb，方向盘转动最大角速度为φmax，轴距为L，前轴中心点等效转角与方向盘转角之比为k，则前轴中心点等效转角转动最大角速度ω=kφmax。后轴中心点的初始位置是坐标轴的原心，车辆的初始方向角与X轴重合。

车辆的横摆角速度：

ωc=Vbtan(ωt)/L

(1)

车辆在t时刻的横摆角：

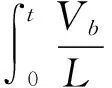
(2)

车辆后轴中心点坐标：

如图1所示，曲线OA段即为车辆从初始平行位置行驶至一侧方向盘打死过程中车辆后轴中心点的轨迹。车辆在A点时，方向盘已处于打死状态，此时车辆的转弯半径即为最小转弯半径，车辆的航向角为Ψ，圆心为C点。连接OC，以C为圆心、OC为半径作圆，过O点做此圆的切线，与X轴夹角为μ。OC与Y轴夹角为θ，定义θ为圆心偏置角，易知θ=μ。设此时A点坐标为(XA,YA),进一步可以计算出：

(5)

θ=arcsin[(XA-RminsinΨ)/R1]

(6)

α=θ+Ψ

(7)

C点的坐标为

(XA-RminsinΨ,YA+RmincosΨ)

(8)

从式(5)～(7)可以看出：在车辆双速确定的情况下，C点、A点坐标及R1、θ的值都已唯一确定。在方向盘转动角速度确定的情况下，车辆在曲线OA段的时间随之确定，车速越高，则A点的横、纵坐标值越大；在车速一定的情况下，方向盘转动角速度与车辆在OA段的行驶时间成反比关系，方向盘转动角速度越快，A点的横、纵坐标值越小。

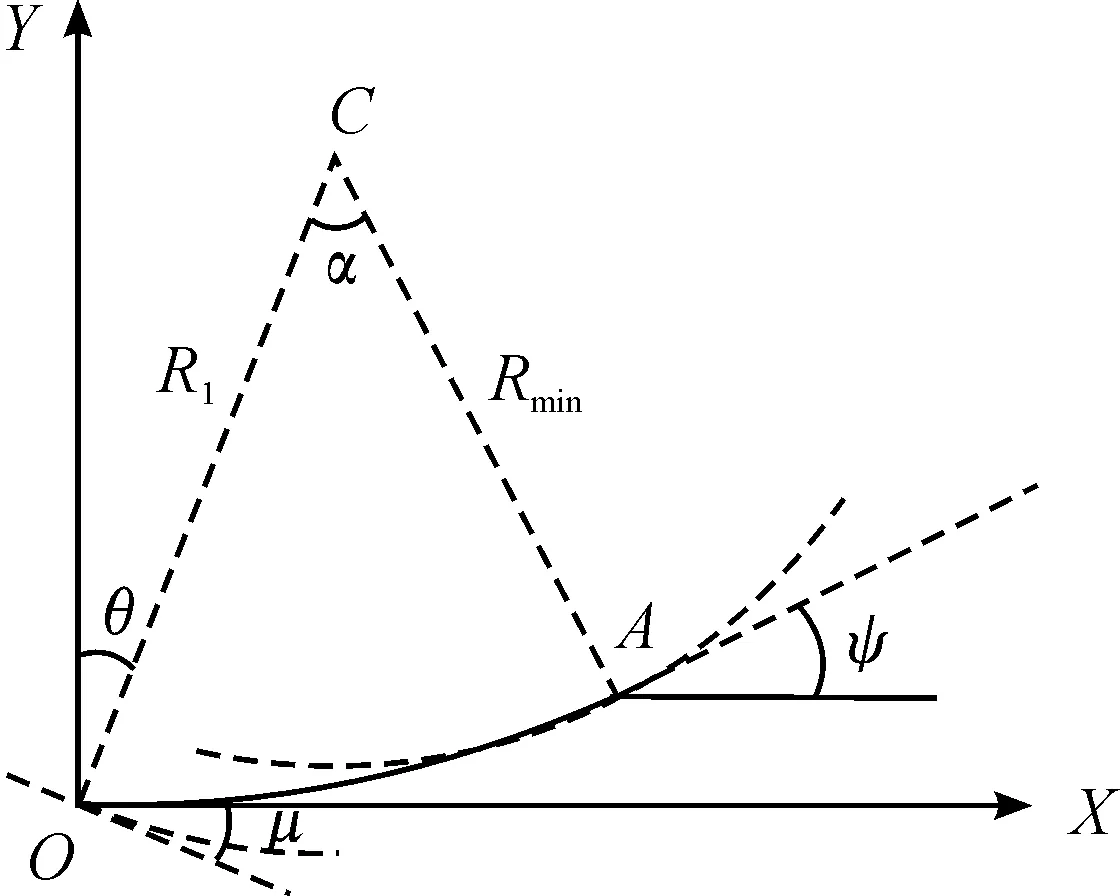
图1 双匀速轨迹

以上给出了车辆从平行位置前行且匀速转动方向盘直至一侧打死的情况下车辆后轴中心点的轨迹，在此基础上可以进一步推出车辆后轴中心点在方向盘“打死—保持—松开”时的运动轨迹(如图2所示)。其中：OA段是方向盘打死阶段；AB段是方向盘保持阶段；BD段是方向盘松开阶段。以C为圆心作出2个分别以Rmin和R1为半径的圆弧，车辆后轴中心点的运动轨迹在2条圆弧所组成的环形区域内。本研究将C点定义为车辆后轮轨迹线(如图2中实线所示)的等效圆心，同时引入2个概念：Rmin为“过渡半径”；R1为“切入半径”。

图2 过渡半径与切入半径

如图3所示，车辆起始点为O点，目标点为E点。如果采用相切圆弧来规划路径必然会存在一个切点，在此点曲线曲率发生跳变，不利于车辆的跟踪控制。而“切入半径”的引入就是为了在解决这一问题的同时不会引入过大的计算量。本文已经讨论过车辆起步的轨迹特点，同时也得到了切入半径R1、过渡半径Rmin以及等效圆心C的位置坐标的计算方法。有了这些参数后就可以在初始点与目标点之间用切入半径来规划双圆弧路径，然后用车辆双匀速运动轨迹处理得到的双圆弧路径，经过处理后的路径在两圆弧相交处用平滑的曲线过渡，避免了路径曲率的突变，同时也符合车辆低速运动特点。

图3 起始点到目标点的双匀速轨迹

用此方法规划出的车辆轨迹线是按照实际车辆数学模型的行驶轨迹规划出来的，在车辆低速行驶的情况下，车辆的动态性能基本比较稳定，用此方法规划出的路径具有一定的可执行性。

2 泊车运动轨迹规划

首先建立车辆数学模型。在双速恒定的情况下泊车入位，此时后轴中心点的轨迹即为满足条件的泊车路径。为了尽可能地减小最小泊车位长度，应保证车辆从D点开始尽快进入以Rmin为半径的弧线路径，则双匀速轨迹作为路径的曲率过渡段应保证方向盘转速尽可能地快，车速尽量慢。对于特定车辆而言，方向盘由EPS的转向电机控制，选取电机所能支持的最大稳定转速作为方向盘转速，车速略高于车辆最低稳定车速。在双速和车辆确定的情况下可以由式(5)(6)得到此车辆所对应的切入半径和圆心偏置角，由此可确定等效圆心的位置。切入半径和圆心偏置角作为车辆的固有属性，在泊车路径规划中直接调用。

如图4所示，在平行泊车情况下，对于特定车辆，在目标点O点和起始点E点之间用2段以车辆切入半径的长为半径的相切圆弧规划出“双圆弧路径”，2个位置的圆心位置可由车辆切入半径和圆心偏置角求得。

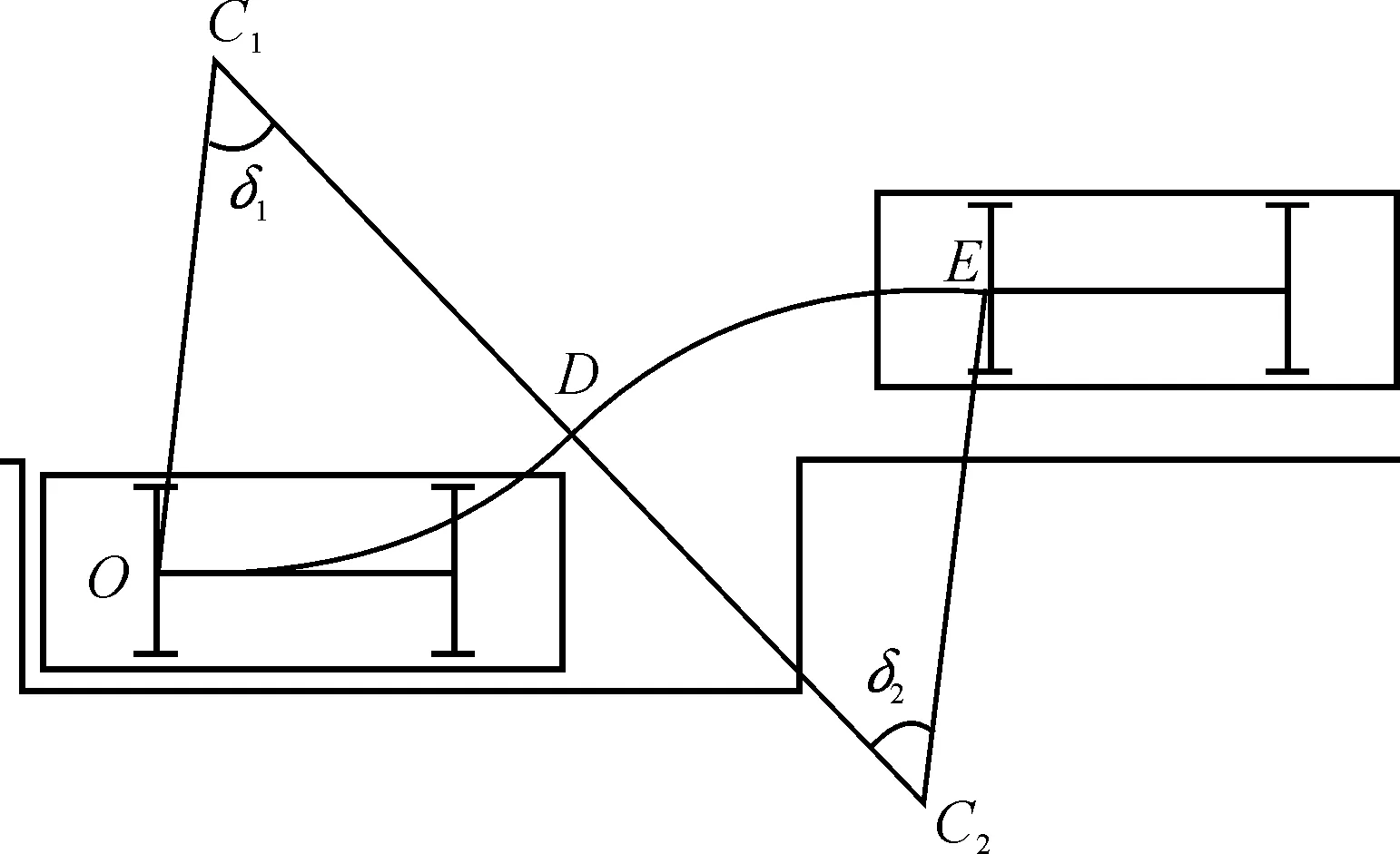
图4 “双圆弧”泊车路径

如图5所示，基于本文对双匀速轨迹、切入半径和过渡半径相互关系的分析，在以切入半径为圆弧的双圆弧路径已经生成的情况下，可以进一步得出一条符合前驱车辆运动学且曲率连续变化的曲线。

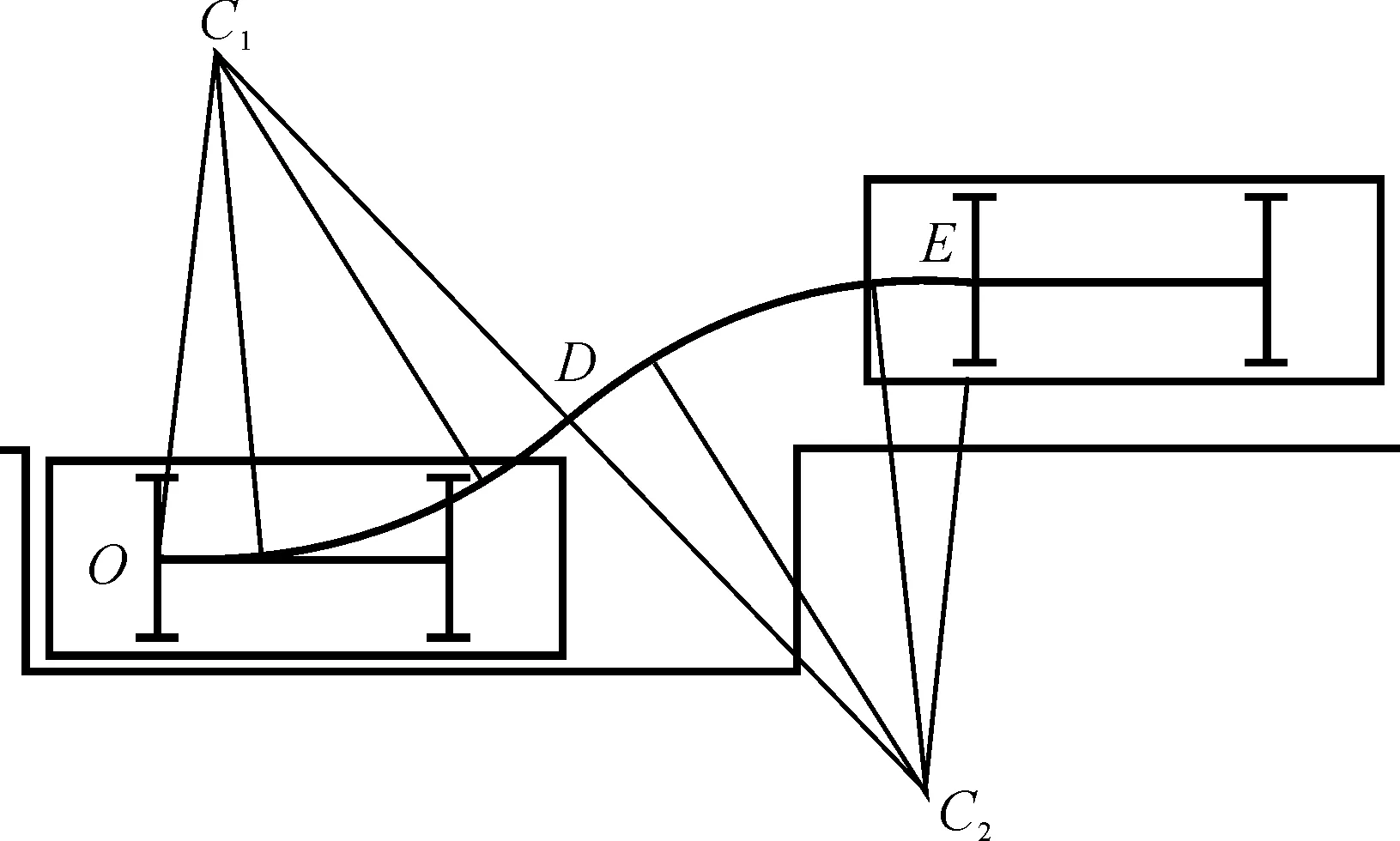
图5 双匀速泊车轨迹

以上的双匀速轨迹参数是建立在车位最小的基础之上，所得到的泊车轨迹也是此种方法所能应对的最小车位尺寸。对于实际泊车空间比较大的情况，为了减少系统的计算量，仍然采用上面的路径规划方法。

3 车辆最小泊车位及避障分析

3.1 最小泊车位分析

如图6所示，车辆轴距为L，前悬长Lf，后悬Lr，车宽为2h。在此基础上首先分析泊车所要求的最小车位长度Lmin。

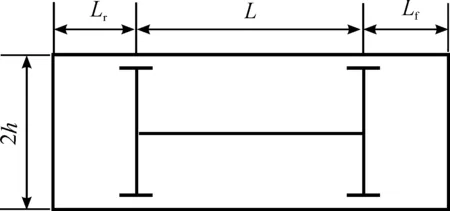
图6 车辆几何尺寸

为了尽量减小Lmin，考虑泊车的终止点为车辆的外廓线与泊车位外沿平齐，且车辆的后端与泊车位的后沿重合，在此状态下考虑泊车所需的最小车位长度(如图7所示)。车辆的4个顶点分别是a、b、c、d，后轴中心O点经过一段双匀速轨迹后到达A点。一般情况下，为了尽量减小泊车位的长度希望方向盘转速尽量地快，因此曲线OA段一般比较短。车辆的右前端点c的运动轨迹最终决定了泊车位所要求的最小长度。当车辆后轴中心点经过双匀速轨迹到达A点时，c点的行驶轨迹也形成了曲线cc′。c点在车辆移出泊车位的过程中的轨迹分为2段：一段是曲率不断变化的cc′；另一段是以RL为半径的圆弧。由于车辆在OA段用时比较短且此段时间内车身横摆角变化也比较小，cc′段仍然会在泊车位内部，因此决定车位最终的长度是以RL为半径的圆弧段。设此段圆弧与泊车位外沿相交于F点，则a点到F点的距离即为泊车位所需的最小车位长度。

从式(9)(10)可以看出：Lmin的大小与R1、Rmin、θ以及车辆的外廓尺寸有关系，而R1、Rmin、θ的值又取决于车辆在双匀速区间内的行驶速度和方向盘转速。因此，可以得出在车辆双速确定的情况下，车辆所需的最小泊车位长度Lmin只与车身的外廓尺寸有关。

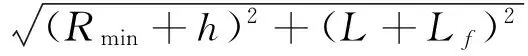
(9)

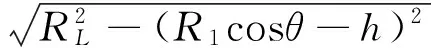
(10)

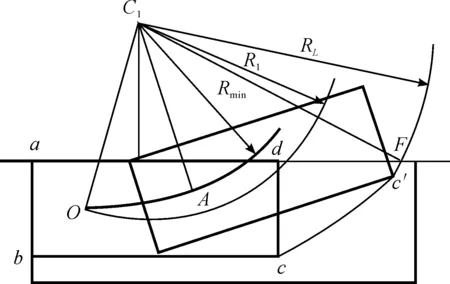
图7 车位最小长度分析

与最小车位相对应，在此状态下车辆泊车所需的最小泊车宽度为Wmin(如图8所示)，此时决定泊车位宽度的关键要素变为车辆右后端的b点轨迹。与以上分析车位长度的方法相似，当车辆后轴中心点由O点到达A点时，b点移动到了b′点，此后以Rb为半径绕C1作圆弧运动。

首先分析曲线bb′段，此时车辆是在双匀速运动阶段，bb′段的轨迹计算公式较为麻烦且不易求解。为了方便求解可以做以下假设：① 假设车辆后轴中心线轨迹OA段为水平直线；② 车辆自身的横摆运动不能忽略，车辆的横摆角在OA段逐渐增加。则可以得出在bb′段所要求的最小泊车位宽度Wbb′：

Wbb′=LObsin(γ+Ψ)+h

(11)

式中：LOb为车辆后轴中心点到车辆右后端的距离；γ为Ob与bc之间的夹角；Ψ为车辆在OA段所能达到的最大车身横摆角；b为车宽的0.5倍。

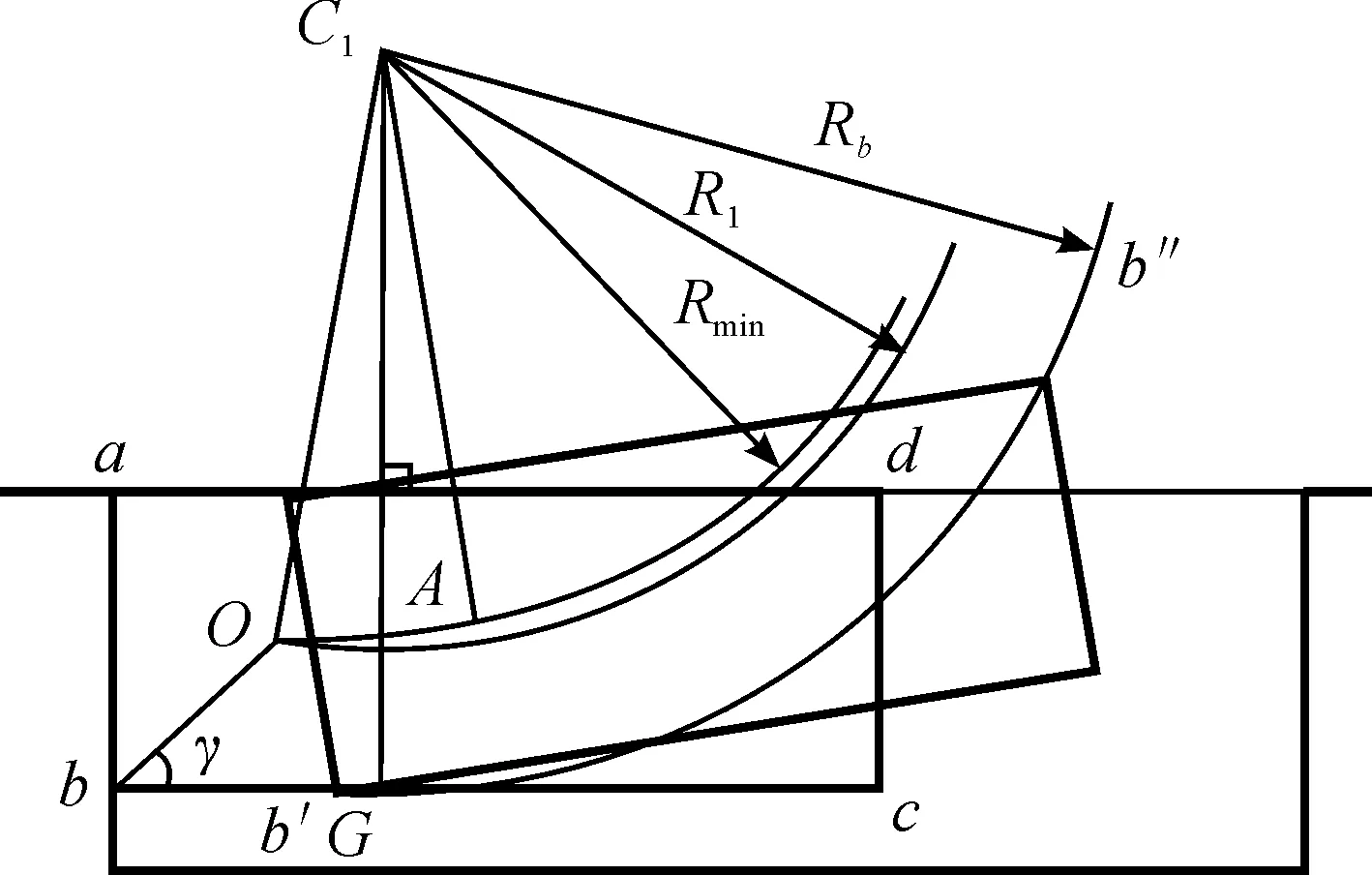
图8 车位最小宽度分析

经过实车计算得出：在实际泊车中，为了尽量大地减小泊车位长度，方向盘转速要尽可能地快；同时由于后轴中心点作为车辆横摆运动的中心，其运动过程中的曲率变化也比较小。车辆后轴中心点在OA段走过的距离和曲率的变化都比较小。表明第1条假设具有一定的可行性。

车辆在b′b″段是一段以Rb为半径、C1为圆心的圆弧，这段圆弧中所能达到的最“深”点决定了此过程中所要求的最小泊车位宽度Wb′b″。过C1点作一条垂直于车辆纵向方向的垂线与弧b′b″相交于G点，易知G点为弧b′b″所能到达的最“深”点。对此也分为两种情况：

1)b′点的横坐标不大于C1点横坐标，此时最小泊车位宽度可以表示为：

Wb′b″1=Rb-R1cosθ+h

(12)

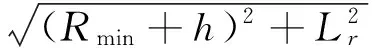
(13)

2)b′点的横坐标大于C1点坐标时，此时圆弧b′b″的最“深”变为了b′点，小泊车位宽度可以表示为

Wb′b″2=LObsin(γ+Ψ)+h-YA

(14)

式中：Ψ为车辆后轴中心点在A点时能的横摆角；YA表示车辆后轴中心点从O点到A点的纵向位移。

可以得出最小泊车位宽度的表达式：

Wmin=max{Wbb′,Wb′b″}

(15)

3.2 泊车避障及可行泊车区域分析

本文泊车路径规划的生成过程是假设车辆从泊车位移出至预备停车位的车辆轨迹线。如图9所示，在整个过程中车辆避障主要考虑4个方面：① 车辆c点与车位线P点的位置关系(此方面主要与车位长度有关，本文已有分析)；② 车辆b点与车位底线的位置关系(此方面主要与车位宽度有关，本文已有分析)；③ 车辆d点与道路边界的位置关系，此关系决定了预备停车位到道路边界的距离；④ 车身I点(车辆后轴与一侧车身交点)与P点的位置关系，此关系决定了预备停车位与车位线的距离。

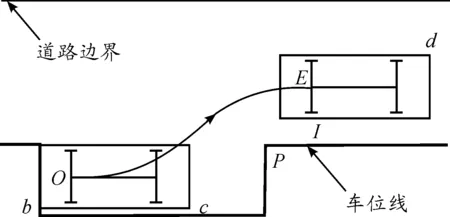
图9 泊车避障示意图

3.2.1 道路边界避障问题

车辆在预备停车位开始倒车入库的阶段同样采用双匀速曲线连接直线与圆弧。如图10所示，车辆后轴中心在GH段是双匀速轨迹曲线，此阶段对应车辆定点dd′段；后轴中心在HG段是一条以Rmin为半径的圆弧，此阶段对应于车辆顶点d′d″段，d′d″段是以O′为圆心、Rd′为半径的圆弧。为了尽量提高泊车效率，dd′段是比较短的，而d′d″段最终决定了车辆预备泊车位与道路边界的最小距离d1。

d1=Rd′-R1cosθ-h

(16)

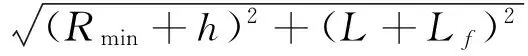
(17)

3.2.2 车位线P点避障问题

考虑P点对泊车过程的影响主要考虑泊车中第2段弧线，即以图11中C2为圆心的曲线，此段曲线由2条车辆双匀速曲线、1条圆弧线组成。由车辆转向原理可知，在不考虑轮胎侧偏的情况下，车辆的瞬时转动中心在车辆后轴的延长线上(此延长线与一侧车身交于I点)，由此可以得出：讨论车辆与P点的避障问题实质上就是讨论车身上I点与P点的相对距离问题。

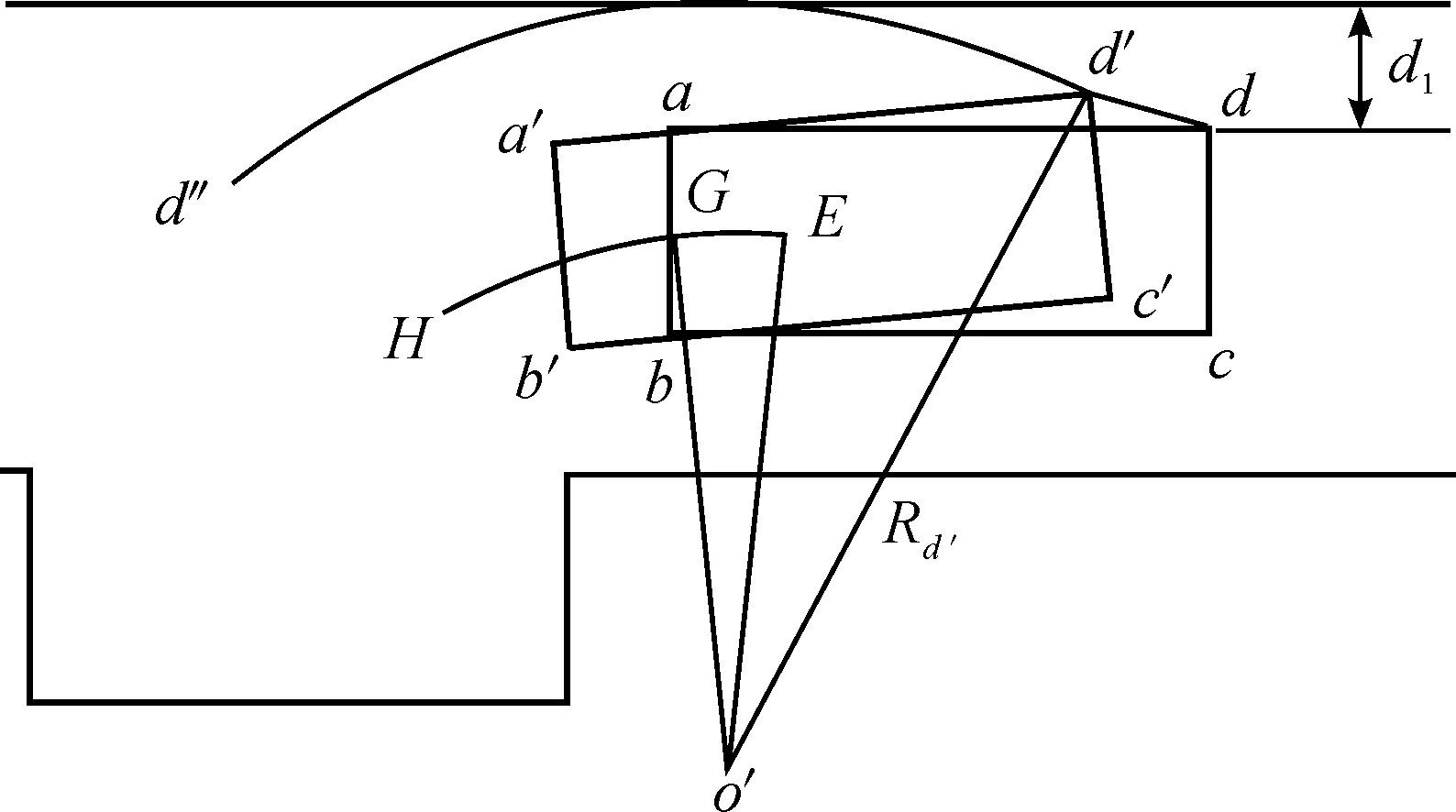
图10 道路边界避障示意图

如图11所示，车辆后轴中心从E点移动到D点(D点为2条切入半径的切点)，车身上的I点移动到了I′点，曲线II′同样由3条曲线组成。为了简化分析，参考文献[14]，采用I点运动的包络线来分析避障问题。因为I点在此运动阶段的运动轨迹一直为凸曲线，I点的下包络线即为直线段II′，因此只需要分析直线段II′与P点的位置关系即可以解决车辆的避障问题，同时也保证了I点和P点在运动过程中有足够的余量。

图11 车位线P点避障示意图

当直线II′过P点时可以确定此时E点坐标:

EX=4R1cos(π/2-θ-λ)cos(λ)

(18)

EY=4R1cos(π/2-θ-λ)sin(λ)

(19)

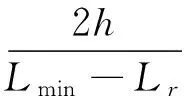
(20)

易知此时车辆与车位线的距离即为预备泊车位与车位线的最小距离：

d2=EY-2h

(21)

3.2.3 可行泊车区域分析

车辆可行的预备停车位置仍然集中于车辆后轴中心点的可行位置范围。如图12所示，通过切入半径R1规划出泊车的双圆弧路径，且两段圆弧圆心角相等(δ1=δ2)。以目标泊车位的后轴中心点为坐标原点建立坐标系，可以推导出预备泊车点E的函数关系(设E的横纵坐标分别为EX、EY)：

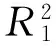
(22)

考虑车辆与道路边界的避障问题有以下不等式成立：

Ld-EY≥d1+h

(23)

考虑车辆与车道线P点的避障问题有以下不等式成立：

EY-2h≥d2

(24)

综合以上3个约束条件即可确定E点的可行域。以国内某款轿车为例，计算其在双匀速泊车路径规划中后轴E点的可行域，如图12所示，其中曲线E1E2段即是车辆后轴中心点的可行区域。经过计算得到车辆与道路边界的最小距离d1=1.11 m，车辆与车位线的最小距离d2=0.29 m。

图12 E点可行区间

图13是曲线E1E2段到O点的双匀速路径。由E1E2段可行线段进一步拓展，沿着E1E2段曲线水平向右的区域都是泊车可行域(如图13所示)，在这一区域内的车辆都可以通过倒车到达线段E1E2的对应点，并且可以平滑地切入已经规划好的泊车路径。

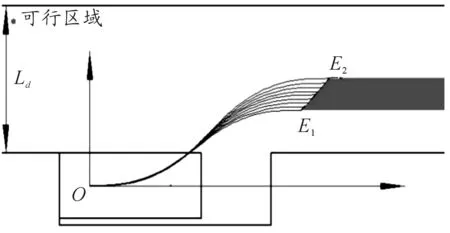
图13 泊车可行域

对于圆弧E1E2段上每一个切入点都唯一对应着由切入半径R1规划的双圆弧路径，E1E2段任意一点的坐标都对应着唯一的δ1：

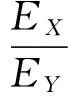
(25)

本文已说明对于特定的车辆在任何可行的泊车空间都采用相同的双匀速轨迹作为泊车路径曲率过渡段，双匀速轨迹相对于过渡圆心的转角α可由式(6)(7)确定。每一个δ1转角都由2个定值α和圆心角η组成(如图2所示)，易得：

η=δ1-2α

(26)

4 仿真验证

以上所建立起的泊车路径是在车速恒定和方向盘转速恒定的基础上得出的。针对实际情况，转向电机的启动加速时间极短，可以近似忽略电机的启动加速时间。文献[11-12]中运用PID闭环控制可以将车速控制在理想范围之内，近似实现匀速泊车过程。

为了更好地模拟实际泊车过程并验证本文所规划出的路径是否适用于实际情况，采用车辆动力学软件Carsim中的车辆模型进行自动平行泊车仿真，并记录泊车过程车速变化情况。

本文在郭孔辉院士的预瞄-跟随理论驾驶员模型[15]的基础上建立车辆倒车运动的驾驶员模型，使用Simulink搭建倒车驾驶员模型，与Carsim联合仿真对泊车轨迹的可行性进行分析比较研究。

基于Carsim中具体的车辆模型参数建立与之相对应的双匀速泊车路径。采用上面的倒车驾驶员模型分别对双匀速泊车路径和双圆弧泊车路径进行泊车仿真，结果见图14、图15。

仿真过程也会考虑实际车辆起步加速和刹车停止时的速度变化，较为真实地反映出实际泊车情况(如图16所示)。由图14、图15可以清晰地看出：应用不同的跟踪方法泊车路径有着明显的区别。对于双圆弧路径而言，由于路径中存在曲率间断点，在车辆连续行驶的情况下很难做到精准的轨迹跟踪。如图16所示，在泊车过程后端车辆跟随误差迅速增大，最终导致泊车失败。而在基于双匀速建立的泊车路径下，泊车过程后期同样存在着误差的波动，但是这种波动都比较小，基本在4 cm以内，车辆最终的方位角不足4°，可以认为车辆已经成功泊车入位。

图14 双匀速泊车轨迹

图15 双圆弧泊车轨迹

由图16可以发现：车速对于泊车轨迹跟踪有较为明显的影响。在泊车前期车辆处于起步阶段，速度较慢，此时跟随效果较好；而在泊车过程后期，车速超过3.6 km/h的阶段也是轨迹跟随稍有波动的阶段。但是总体而言，基于双匀速建立的泊车轨迹在非匀速泊车过程中同样可以作为合理、连续的参考泊车路径。

基于双匀速轨迹推导出的泊车路径是将车辆几何构型和车辆对路径连续性的要求综合考虑而得到的，同时仿真实验也证明：基于双匀速轨迹推导出的泊车路径可以作为指导车辆泊车入位的参考路径。

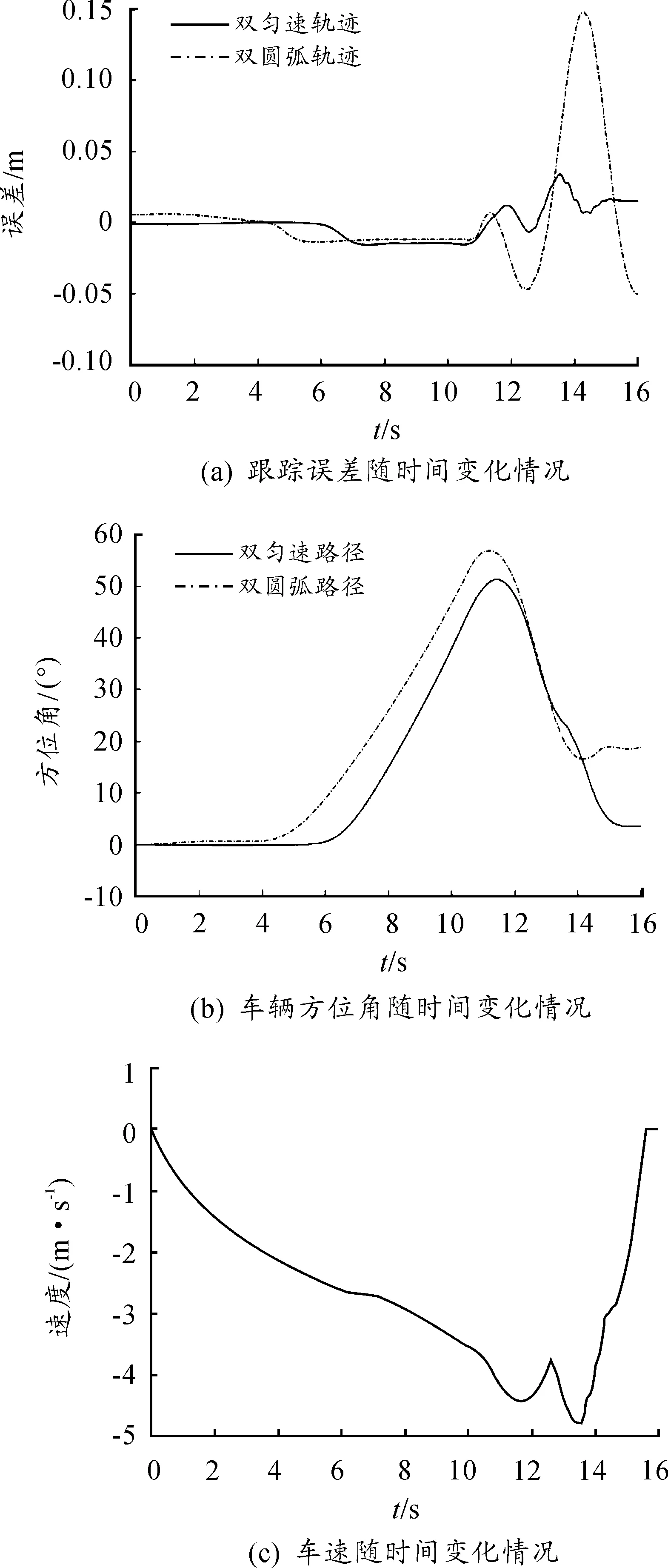
图16 跟踪误差、车辆方位角及车速随时间的变化情况

5 结束语

本文分析了车辆在双匀速情况下泊车过程中后轮轨迹的特点，同时与双圆弧泊车路径有机地结合在一起，由此规划出一条曲率连续变化且符合车辆运动学的泊车路径。仿真结果表明：此条由车辆匀速推导出的路径对于车辆非匀速泊车的情况同样有效。

本文只考虑了泊车初始位置与车位线平行的情况，同时本文中过渡半径始终为车辆最小转弯半径，在后续研究中应灵活运用过渡半径，扩大泊车可行域。对于非平行初始位置的情况也应考虑运用双匀速规划路径，使此方法有更大的适用性。

虽然双匀速路径解决了泊车路径曲率不连续的问题，但是由于不能出现停车转向的情况也增加了泊车位的长度。后续考虑将多步式泊车方法与双匀速轨迹相结合，使泊车所需空间最小化。

仿真实验证明：在非匀速泊车过程中，双匀速轨迹同样可以作为合理的泊车路径。下一步将尝试用理论证明双匀速在非匀速时的轨迹特点，并将其运用到泊车路径跟踪方面，进一步完善双匀速泊车轨迹规划与跟踪方法。

[1] WANG Chunxiang,ZHANG Hengrun,YANG Ming,et al.Automatic Parking Based on a Bird’s Eye View Vision System[J].Advances in Mechanical Engineering， 2014(2014):847406.

[2] SUNGWOO C,CLÉMENT B,BRIGITTE D N.Easy Plan Planning and Robust Control for Automatic Parallel Parking[C]//IFAC.The International Federation of Automatic Control.Milano:IFAC.2011:656-661.

[3] REEDS,JAMES,LAWRENCE S.Optimal Paths for a Car that Goes Both Forwards and Backwards[J].Pacific Journal of Mathematics,1900,145(2):367-393.

[4] LIAO Zhao,ZHENG Guoqiang.Automatic Parking Path Optimization Based on Bezier Curve Fitting[C]//IEEE.International Conference on Automation and Logistics.Zhengzhou:IEEE,2012:583-587.

[5] 李红.自动泊车系统路径规划与路径控制研究[D].长沙：湖南大学，2014.

[6] 李红，王文军，李克强.基于B样条理论的平行泊车路径规划[J].中国公路学报,2016,29(9):143-151.

[7] JAEYOUNG M,IL B,JAE G C,et al.A Trajectory Planning Method Based on Forward Path Generation and Backward Tracking Algorithm for Automatic Parking Systems[C]//IEEE.International Conference on Intelligent Transportation Systems.Qingdao:IEEE,2014:719-724.

[8] CHEN C H,HSU C W,YAO C C.A Novel Design for Full Automatic Parking System[C] //IEEE.International Conference on ITS Telecommunications.Changhua:IEEE,2012:175-179.

[9] HÉLÉNE V,SÉBASTIEN G,NICOLETA M E,et al.Automatic Parallel Parking in Tiny Spots:Path Planning and Control[J].IEEE Transactions on Intelligent Transportations Systems,2015,16(1):396-409.

[10] HÉLÉNE V,SÉBASTIEN G,NICOLETA M E,et al.Automatic Parallel Parking with Geometric Continuous-Curvature Path Planning[C] //IEEE.Intelligent Vehicles Symposium.Dearborn:IEEE,2014:465-471.

[11] 钱立军，胡伟龙，刘庆，等.多段式自动泊车路径规划及其关键技术[J].吉林大学学报(工学版)，2016,46(3)：785-791.

[12] 胡伟龙.多段式平行泊车轨迹动态规划及系统控制[D].合肥：合肥工业大学，2016.

[13] 姜辉.自动平行泊车系统转向控制策略的研究[D].长春：吉林大学，2010.

[14] SCHEUER A,FRAICHARD T H.Continuous-Curvature Path Planning for Car-Like Vehicles[C]//IEEE.International Conference on Intelligent Robots and Systems.Grenoble:IEEE,1997:1-7.

[15] 郭孔辉.汽车操纵动力学[M].长春：吉林科学技术出版社，1991.

(责任编辑刘 舸)

TrajectoryPlanningMethodBasedonDoubleConstantSpeedforAutomaticParkingSystems

LI Pan， HUANG Jiang， YANG Hao， HAN Zhonghai

(College of Vehicle Engineering, Chongqing University of Technology, Chongqing 400054, China)

2017-03-09

国家自然科学基金资助项目(51105136)

李攀(1991—),男,河南邓州人,硕士研究生,主要从事车辆动力学研究； 通讯作者 黄江,男,博士,讲师,主要从事车辆动力学、智能驾驶研究,E-mail：huangjiang@cqut.edu.cn。

李攀,黄江,杨浩,等.基于双匀速轨迹的自动泊车路径规划研究[J].重庆理工大学学报(自然科学)，2017(9):36-44.

formatLI Pan，HUANG Jiang，YANG Hao，et al.Trajectory Planning Method Based on Double Constant Speed for Automatic Parking Systems[J].Journal of Chongqing University of Technology(Natural Science)，2017(9):36-44.

10.3969/j.issn.1674-8425(z).2017.09.006

U463.3

A

1674-8425(2017)09-0036-09