基于模糊判断矩阵的两种排序方案
沈 君,苗俊红
(海南师范大学 数学与统计学院, 海南 海口 571158)
基于模糊判断矩阵的两种排序方案
沈 君,苗俊红
(海南师范大学 数学与统计学院, 海南 海口 571158)
模糊判断矩阵的一致性有两种定义,一种是将满足加性传递性的模糊判断矩阵称为一致性判断矩阵,另一种是将满足乘性传递性的模糊判断矩阵称为一致性判断矩阵,在这两种一致性意义下研究模糊判断矩的排序问题,各给出一种排序计算方法,并用实例验证了方法的有效性。
模糊判断矩阵;排序向量;权重
一、引 言
层次分析法(AHP法)在多属性决策中有非常重要的地位,它可以对决策方案进行综合排序或确定属性的权重。决策者把对属性或方案的偏好信息数量化,构造两两比较判断矩阵。判断矩阵分为互反判断矩阵和模糊判断矩阵两种类型,相对于互反判断矩阵,模糊判断矩阵在属性两两重要性的比较上更合理,更符合人类思维判断的一致性[1][2][3]。模糊一致矩阵在模糊综合评判、权重分析、系统分析和系统评价等软科学中得到广泛应用。近年来,模糊矩阵排序研究成为研究热点,取得了丰硕研究成果。
文献[4],文献[5],文献[6]分别提出了中转法,最小方差法和权的最小平方法及特征向量法求解模糊判断矩阵排序;文献[7]提出了模糊判断矩阵的最小一乘、文献[8]提出了用最小偏差法确定模糊判断矩阵排序;文献[9]通过构造函数,将模糊判断矩阵转化为AHP判断矩阵来获得排序;文献[10]提出了模糊判断矩阵的集成方法;还有学者提出了二次规划和非线性规划的方法排序。
模糊判断矩阵的一致性概念不只一种。目前,模糊判断矩阵的一致性有两种定义,一种是将满足加性传递性的模糊判断矩阵称为一致性判断矩阵,另一种是将满足乘性传递性的模糊判断矩阵称为一致性判断矩阵,本文在这两种一致性意义下研究模糊判断矩阵排序问题,各给出了一种排序计算方法,并用实例验证了方法的有效性。
二、基本概念
定义2.1 设模糊矩阵,R=(rij)n×n若0 定理2.1[1]设是阶模糊矩阵,则R是模糊一致矩阵的充分必要条件是存在一个n阶归一化的向量W=(w1,w2,…,wn)T及一个正数a,使得∀i,jrij=a(wi-wj)+0.5成立。 (一)基于积型模糊一致判断矩阵的排序方法 (1) 定理3.1 设模糊判断矩阵R=(rij)n×n,则由(1)求出的排序向量w=(w1,w2,…,wn)满足: ,. 证明 建立Lagrange函数: 对各变量求偏导,并令偏导等于0,得: (2) 对上述方程组中前n个式子求和, (3) 即: (4) 对上面n个式子相加,得: (5) 把(5)式代入(4)式,有: (二)基于加型模糊一致性判断矩阵的排序方法 (6) 定理3.2 设模糊判断矩阵R=(rij)n×n,则由(6)求出的排序向量w=(w1,…,wn)满足: 证明 建立规划模型: 为了求解上述线性规划,构造Lagrange函数: 令: (7) 将(7)中前n个方程相加,得到: 解得λ=0,代入(7)式前n个方程中,得: 例4.1[8]假设一个决策者对决策方案集提供的模糊判断矩阵为: 利用定理3.1,得模糊互补判断矩阵B的排序向量:w=(0.171,0.478,0.239,0.112),排序方案为x2≻x3≻x1≻x4。利用定理3.2,得模糊判断矩阵B排序向量为w=(0.233,0.350,0.250,0.167),排序方案为x2≻x3≻x1≻x4。文献[8]中方法得到排序向量为:w=(0.1732,0.4326,0.2343,0.1599),与本文方法对比,虽然排序向量略有差异,但是排序方案都是相同的。 例4.2[8]设某一多属性决策问题有4个属性ui,i=1,2,3,4,为了确定他们的权重,专家对wi,i=1,2,3,4,利用0.1~0.9五标度进行两两比较,并给出模糊判断矩阵: 文献[8]提到有学者用中转法、最小方差法、最小偏差法、特征向量法得到B的排序向量分别为: w=(0.3000,0.2333,0.2667,0.2000),w=(0.4000,0.2000,0.3000,0.1000), w=(0.4302,0.1799,0.2749,0.1150),w=(0.4303,0.1799,0.2748,0.1150), 利用本文中定理3.1,得B的排序向量为:w=(0.3883,0.1932,0.2951,0.1234),利用本文中定理4.1,得B的排序向量为w=(0.3500,0.2167,0.2833,0.1500)。尽管用不同方法计算出来的排序向量略有差异,但是相应属性排序结果是相同的,即都有x1≻x3≻x2≻x4。 本文针对积型和加型两种模糊一致性判断矩阵与模糊判断矩阵的排序向量之间存在差异问题,通过最小化差异,得到了模糊判断矩阵排序向量两种方案。这两种方案不仅计算简单,而且算例也表明其可行、有效。 [1] 吕跃进.基于模糊一致矩阵的模糊层次分析法的排序[J].模糊系统与数学,2002(2):81-85. [2] 樊治平,姜艳萍.模糊判断矩阵排序方法研究的综述[J].系统工程,2001,19(5):12-18. [3] 和媛媛,巩在武.模糊判断矩阵最优化排序方法研究综述[J].统计与决策,2011,(7):165-168. [4] 徐泽水.模糊互补判断矩阵排序的一种算法[J]. 系统工程学报, 2001, 16(4): 311-314. [5] 徐泽水.模糊互补判断矩阵排序的最小方差法[J].系统工程理论与实践, 2001,21(10): 93-96. [6] 徐泽水.互补判断矩阵的两种排序方法——权的最小平方法及特征向量法[J].系统工程理论与实践,2002,22(7):71-75. [7] 马晓燕,魏立平,国忠金.基于模糊互补判断矩阵的对数最小一乘法及算法程序设计[J]. 数学的实践与认识,2007, 39(9): 63-68 [8] 刘卫锋,何霞.模糊判断矩阵排序向量的最小偏差法[J].模糊系统与数学,2012,26(6):132-134. [9] 肖四汉.具有不同形式偏好信息的群决策理论与方法研究[D].沈阳:东北大学, 2001. [10] 钟小伟,傅鸿源.模糊一致矩阵排序方法的集成 [J].模糊系统与数学,2014,28(2):126-130. [11] 兰继斌等.模糊层次分析法权重研究[J].系统工程理论与实践,2006,(9):107-112. (责任编辑:赵峰) Abstract: Multiplicative and additive consistency of fuzzy judgment matrix are defined. Two Ordering Schemes of priority weight vector are obtained by building and solving two programming models. Two examples are used to illustrate the applicability of the proposed schemes. Keywords: fuzzy judgment matrix; priority vector; weight TwoOrderingSchemesBasedonthePriorityWeightVectorofFuzzyJudgmentMatrix SHEN Jun, MIAO Jun-hong (School of Mathematics and Statistics,Hainan Normal University,Haikou 571158,China) O159 A 1009-9743(2017)03-0150-04 2017-04-05 沈君,女,汉族,河北保定人。硕士。海南师范大学数学与统计学院副教授。主要研究方向:不确定信息处理、高等数学研究。苗俊红,女,汉族,山东德州人。硕士。海南师范大学数学与统计学院副教授。主要研究方向:随机微分方程、概率论 2017年海南省自然科学基金面上项目“复模糊集值函数的积分及其应用研究”(编号:117123)成果之一。 10.13803/j.cnki.issn1009-9743.2017.03.031

三、基于积型和加型模糊一致判断矩阵的排序方法




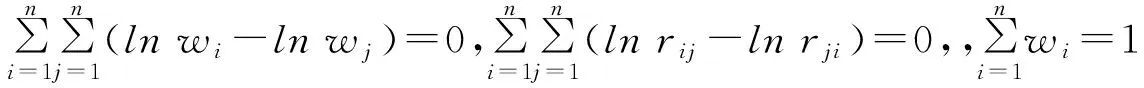

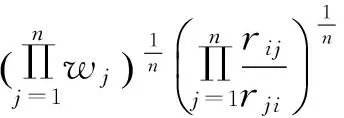


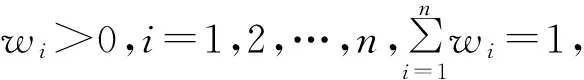

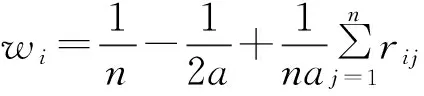



四、算例


五、总 结

