基于快速傅里叶变换和db小波变换的谐波检测

金 攀, 雷景生

(上海电力学院 计算机科学与技术学院, 上海 200090)

基于快速傅里叶变换和db小波变换的谐波检测

金 攀, 雷景生

(上海电力学院 计算机科学与技术学院, 上海 200090)

在电力系统谐波检测中,使用快速傅里叶变换法(FFT)可以得到平稳谐波信号中的频谱,从而可以确定该信号中谐波的频率和幅值等信息.但FFT局限于得到信号的频域信息,很难检测到谐波发生的具体时刻,而小波变换可以捕捉到信号中的细节部分.针对复杂谐波信号,提出了一种将快速傅里叶变换和小波变换相结合的检测方法.由Matlab仿真结果可知,该方法可以检测稳态谐波,确定暂态谐波的突变时刻.

电力系统; 谐波检测; 快速傅里叶变换; 小波变换

随着电网负载的增大及运行时干扰因素的增加,电网中受到谐波污染的几率越来越大,由此造成了电网的能量浪费严重、采样数据异常、用电设备误操作等诸多严重后果[1-5].因此,对电力系统中谐波检测的研究受到了国内外的广泛关注.

目前,对于谐波检测的方法已经趋于成熟,如快速傅里叶变换(Fast Fourier Transform,FFT)对于电力系统中平稳信号的检测效果较好,而对于突变信号的检测效果不佳[6-7].但通过小波变换方法可以检测到信号中突变以及间断点等奇异分量,从而实现对谐波出现时间的准确定位.本文针对检测信号,首先进行离散小波变换,得到信号的低频部分和高频部分,通过模极大值理论分析出信号的突变点[8],然后重构各个频带波形信号,由于低频信号中大部分噪声已经被分离出去,通过快速傅里叶变换可以得到相应的波形频谱[9-10]及谐波次数,最终完成对谐波的检测.

1 基本理论

1.1 快速傅里叶变换的原理

傅里叶变换可以将信号函数的时域表现形式转换成频域表现形式,其本质就是在信号函数S(t)满足狄里克莱条件时,即满足有且只有一个间断点和只有有限个极值时,就可以将其进行傅里叶变换[9].信号函数的傅里叶变换过程就是将该函数分解成不同频率的正弦波之和.傅里叶变换的数学表达式为[11]:

(1)

式中:f(t)——连续非周期的时间信号函数,可以通过傅里叶变换分解成若干个正弦函数之和;

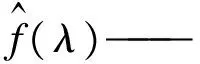
目前在工程中,广泛采用快速傅里叶变换进行信号分析,它能得到信号函数的各个频谱分量,因而FFT被称为谐波分析的高效方法.但在捕捉信号的局部信息时,FFT存在天然的缺陷,信号在任意时刻的变化都会对整个频率造成影响.通过改进快速傅里叶变化的算法得到的短时傅里叶变换(STFT),能够在获取信号的局部信息的同时,改善FFT在时间分辨率上的不足,但由于其窗口函数的限定,对于时间分辨率和频率分辨率方面的问题仍然束手无策.加之STFT没有对应的快速算法,故在工程应用中很难推广[12].

1.2 离散小波变换的原理

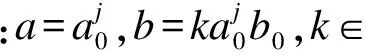
(2)

在实际谐波分析过程中,由于信号函数x(n)是由采样得到的,所以x(n)最终是以离散形式进行处理的.一般情况下,设a0=2,b0=1,对尺度和偏移进行二进离散,即a0=2j,b=2jk,k∈Z,从而得到二进小波[7],即:

(3)

1.3 Mallat算法原理

Mallat算法是在多分辨率分析思想的基础上发展而来的,是小波变换的一种快速算法.该算法由小波分解滤波器及小波重构滤波器实现信号的分解与重构[13].假设原始信号用S(n)表示,谐波分解可以表示为:

A0[s(n)]=x(n)

(4)

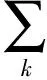
(5)

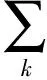
(6)

式中:s(n)——含有谐波的信号函数;j——分解层数;Aj——小波系数的近似部分,即谐波信号的低频分量;

Dj——小波系数的细节部分,即谐波信号的高频分量;

H——低通滤波器;

G——高通滤波器.

通过选取合适的小波基函数,确定H和G的参数.在分解过程中,低频Aj中丢失的信息由高频Dj捕获.在进一步分解中,将Aj分解成低频Aj+1和高频Dj+1两部分,低频Aj+1中丢失的信息由高频Dj+1捕获.以此类推,最终得到信号的精细的时频特征,即不断地将信号分解成不同频率带上的信号分量[10].

采用上述方法对信号进行不断分解,即可在不同分辨率下分别观测原始信号的近似部分和细节部分.采用 Mallat算法对信号进行重构的过程则与分解过程相反.重构算法可表示为[14]:

(7)

式中:j=J-1,J-2,J-3,…,1,0.

2 Matlab仿真实验及分析

假设电网异常运行状况下出现的稳态谐波分量为fa(t),瞬态谐波分量为fb(t),因用电设备异常运行的随机噪声干扰信号为fc(t),特定时间加入的瞬态谐波分量为fd(t).电压复合信号S(t)由上述若干个信号分量组成[3].

在Matlab仿真实验中,其中谐波频率f1=50 Hz,f2=150 Hz,f3=250 Hz,f4=350 Hz,f5=550 Hz,f6=650 Hz,f7=850 Hz,f8=900 Hz.

电压的复合信号1可以表示为:

S(t)=fa(t)+fb(t)+fc(t)

(12)

该复合电压信号S(t)波形如图1所示.

图1 原始信号波形

当我们需要检测到电力系统中的最高次谐波次数为60,根据采样定理,设采样频率为6 400 Hz,采样点数N取2 048,截断信号长度取前1 000点.通过仿真可知,选取db20小波进行分解,分解层数选取4时高、低频率带划分的效果更明显;Mallat算法每次对信号进行分解后都会丢弃细节部分(高频部分),而对近似部分(低频部分)继续分解,4层频带频率理论上的分布如表1所示.对上述复合信号进行小波变换,得到的高低频分解系数如图2和图3所示.

表1 4层频带的频率分布

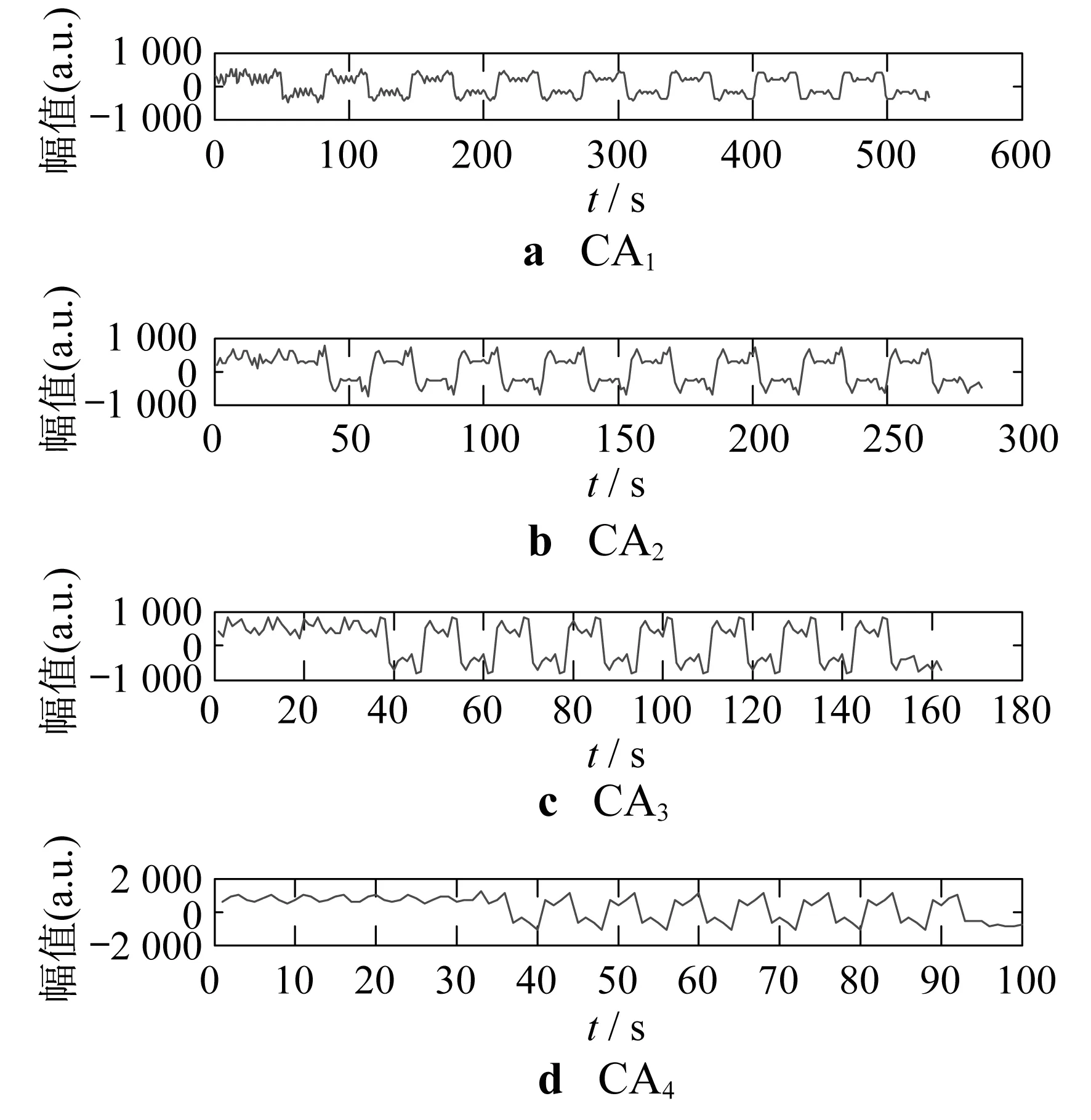
图2 低频系数

图3 高频系数

经过db20小波变换后,复合信号被分解成了稳态部分和非稳态部分,并可以准确地定位出3,5,7,11,13次谐波所在的小波变换低频系数CA2频带范围,也就是0～800 Hz,该频带包含了全部稳态分量.

通过对CA2低频系数进行重构可以得到稳态信号波形,如图4所示.并将该信号进行快速傅里叶变换,得到信号的频谱如图5所示.从图5中也可以找到3,5,7,11,13次谐波.

图4 稳态信号谐波波形

图5 稳态信号频谱

重构CD2高频系数,其谐波波形如图6所示.由图6可知,随着时间的增加,谐波波形出现衰减的趋势,这与fb(t)=100sin (2πf7t)e-20t的理论信号一致.

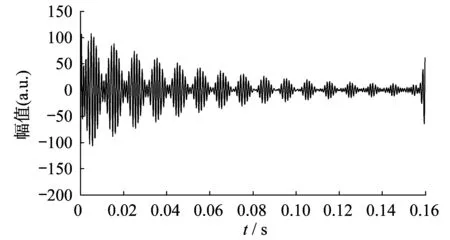
图6 瞬态信号谐波波形

在现代电力系统谐波检测中,不仅要检测到谐波的次数,而且还要得到谐波出现的时间和持续的时间,这样有助于我们快速地采取保护措施,避免谐波对电气设备造成损害.

电压的复合信号2可表示为:

S(t)=fa(t)+fd(t)+fc(t)

(13)

在100～120采样点加入瞬态谐波分量fd(t),也就是fd(t)持续时间t为0.015 6～0.018 7.当对CD1频带系数进行重构时,发现在0.015 6～0.018 7时间内信号的波动幅度很大,如图7所示.由此可以准确地定位到非稳态信号的起止时刻.

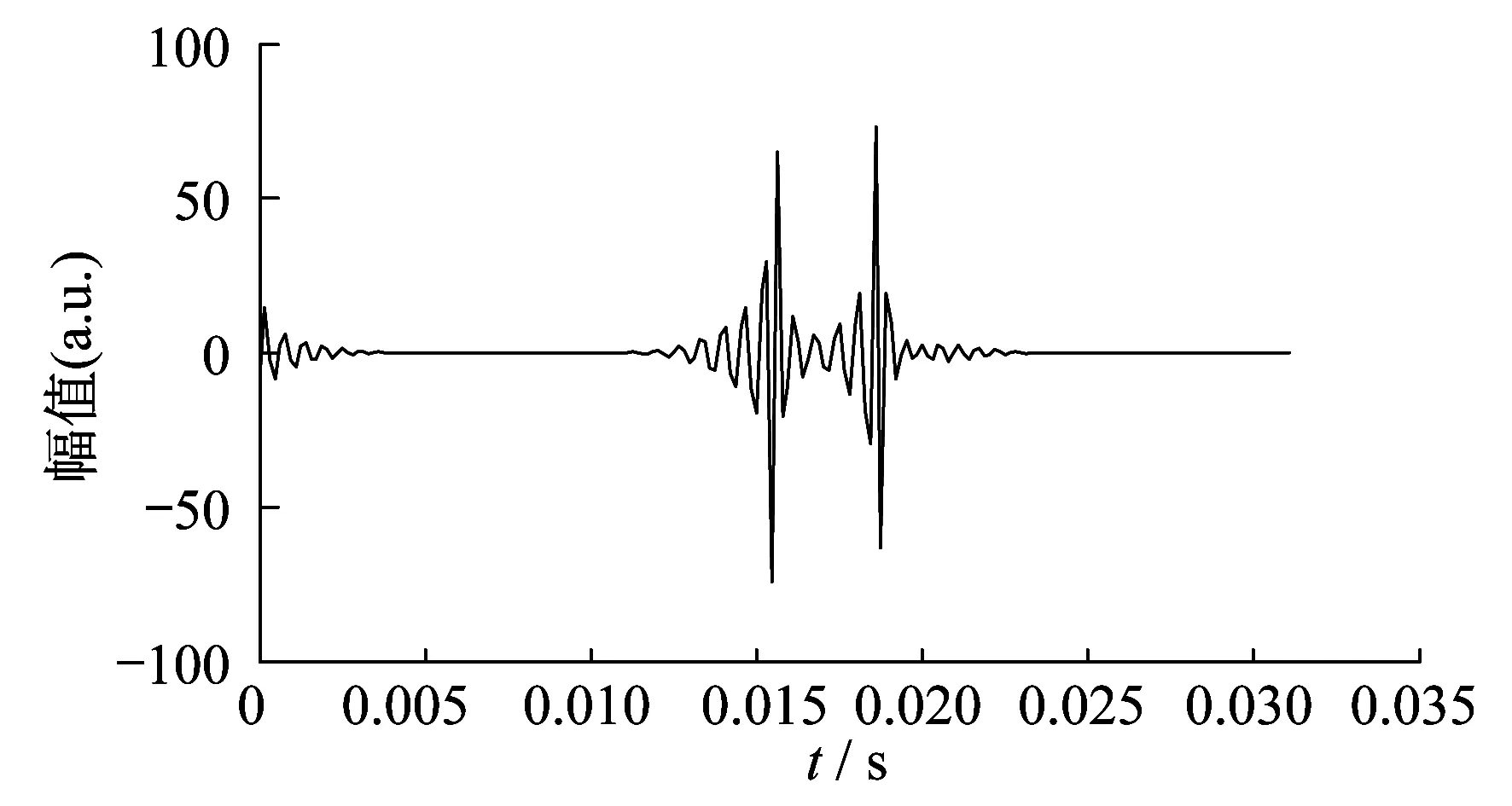
图7 CD1频带系数波形重构示意

3 结 语

本文根据待检测谐波信号的特点,并结合快速傅里叶变换和小波变换在谐波检测中所具有的优势,提出了快速傅里叶变换和小波变换相结合的综合检测方法.首先利用小波变换将信号分解稳态部分和暂态部分,然后根据自身特点进行下一步处理.稳态部分采取快速傅里叶变换法得到频谱图,非稳态部分通过确定突变点,从而推测出高频谐波的发生位置,并且重构出该信号波形进行分析.从实验仿真结果可以看出,这种综合检测方法既能检测瞬态信号,又能精确地定位各次谐波,同时还可以获取谐波在时域和频域上的完整信息,这为谐波治理的前期阶段提供了一定的理论分析基础.

[1] 雷汝海,郝震.基于小波变换Mallat算法的电网谐波检测方法[J].工矿自动化,2014(12):65-69.

[2] 桑松,柴玉华,孙影.基于小波变换和快速傅里叶变换的谐波检测[J].电测与仪表,2012(7):29-32.

[3] 朱翔,解大,高强,等.基于FFT和db20小波变换的电力系统谐波联合分析策略[J].电力系统保护与控制,2012(12):62-65.

[4] 房国志,杨超,赵洪.基于FFT和小波包变换的电力系统谐波检测方法[J].电力系统保护与控制,2012(5):75-79.

[5] 房国志,杨才山,杨超.基于Meyer小波和FFT的电网间谐波检测[J].电力系统保护与控制,2011(12):90-93.

[6] 刘蓉晖.基于小波技术的电网暂态谐波检测[J].低压电器,2011(4):47-50.

[7] 罗冠姗,卢惠辉,苏成悦,等.一种基于小波包变换的电力谐波检测方法[J].电力建设,2015(3):71-76.

[8] 李战明,刘燕.基于FFT和小波变换的谐波分析策略[J].工业仪表与自动化装置,2014(2):96-98.

[9] 熊杰锋,李群,袁晓冬,等.电力系统谐波和间谐波检测方法综述[J].电力系统自动化,2013(11):125-133.

[10] 赵惠玲,周芸.基于小波变换的电力系统谐波检测的研究[J].电子设计工程,2012(1):77-80.

[11] 刘争艳,郑恩让,马令坤.基于Matlab的非平稳谐波检测方法仿真研究[J].化工自动化及仪表,2011(1):69-71.

[12] 王晶晶,杨勇.基于小波变换和加Hanning窗FFT的谐波检测新方法[J].自动化应用,2010(4):63-66.

[13] 陈宇,段哲民.小波多分辨率算法在电力谐波检测中的应用[J].计算机测量与控制,2008(10):1 493-1 495.

[14] 海涛,邵红硕,王钧.基于db小波变换和降噪的电力系统间谐波分析[J].陕西电力,2010(11):28-31.

(编辑 胡小萍)

HarmonicDetectionBasedonFFTanddbWaveletTransform

JINPan,LEIJingsheng

(SchoolofComputerScienceandTechnology,ShanghaiUniversityofElectricPower,Shanghai200090,China)

In the harmonic detection of power system,Fast Fourier Transform(FFT) is applied to get the Spectrum of the steady-state harmonic signals so that the frequency,amplitude and other information of the harmonics in the signal can be determined.Since the FFT is limited to obtaining the frequency domain information of the signal,it is difficult to detect the specific moment of occurrence of harmonics,but the Discrete Wavelet Transform (DWT)can capture the details of the signal part.Aiming at complicated harmonic signals,a method is presented to combine FFT and wavelet transform.The simulation results by Matlab show that the method can detect the steady-state harmonics and determine the sudden change of transient harmonics.

power system; harmonic detection; fast Fourier transform; discrete wavelet transform

10.3969/j.issn.1006-4729.2017.04.006

2017-03-09

金攀(1992-),男,在读硕士,江苏高邮人.主要研究方向为基于无线传感器网络的工业用电监测.E-mail:2270531667@qq.com.

TM76;O174.2

A

1006-4729(2017)04-0337-04