基于PSO改进的T-S模糊神经网络短期电力负荷预测研究
沈 娟, 刘大明
(上海电力学院 a.自动化工程学院; b.计算机科学与技术学院, 上海 200090)
基于PSO改进的T-S模糊神经网络短期电力负荷预测研究
沈 娟a, 刘大明b
(上海电力学院 a.自动化工程学院; b.计算机科学与技术学院, 上海 200090)
精确的电力负荷预测有利于保障电网运行的安全性、稳定性、高效性及经济性.为提高预测精度,采用了一种PSO改进T-S(Takagi-Sugeno)模糊神经网络方法.分析了数据预处理对改善输入量的重要性,讨论了可以让学习率和平滑因子动态调节的改进T-S模糊神经网络算法,从而使PSO找到最优参数,然后结合历史负荷数据、相关影响因素进行预测,以表明改进的T-S模糊神经网络在短期电力负荷中具有更高的控制精度.
预测精度; PSO优化T-S算法; 模糊模型; 异常数据
近年来,随着我国电力市场的建立、发展和完善,负荷预测[1]逐渐成为电力系统经济运行、调度统筹的重要模块,同时也是电力领域内经久不衰的研究课题.许多学者对电力负荷预测进行了大量的研究[2].,如回归分析[3-4]、指数平滑[5]、时间序列[6-7]、大数据[8]等方法都相继被用到短期负荷预测模型中.然而,由于负荷预测具有模糊性和非线性的特点,导致上述方法的预测精度不高,而且遗传灰色神经网络、模糊多目标遗传优化算法等只考虑单一的影响因素,所以效果不明显.支持向量机算法(Support Vector Machine,SVM)可以用于二次规划问题的线性不等式,但训练的样本数目增多时,二次规划就会出现局限性,不能满足高精度预测.极限机器学习分布(MR-OSELM-WA)[9]和新云计算预测方法的研究被证明有更准确的预测精度.但该方法有一个缺点,即在云计算算法中过分依赖大数据.
目前,研究人员专注于解决由参数优化和网络权重随机初始化所导致的网络收敛效果不理想的问题.本文主要介绍了由粒子群优化算法(Particle Swarm Optimization,PSO)改进的T-S模糊神经网络算法[10-11],该算法在提高短期电力负荷预测精度和误差收敛速度方面具有一定的优势.
1 负荷预测分类
电力系统负荷预测分类[12],按用电部门的属性,可分为民用负荷、工业负荷、商业负荷、农业负荷以及其他负荷;按预测表示的特性,可分为最高负荷、负荷曲线、负荷率等;按预测周期的时间,可分为超短期、短期、中期和长期预测等.表1为不同预测周期对比.
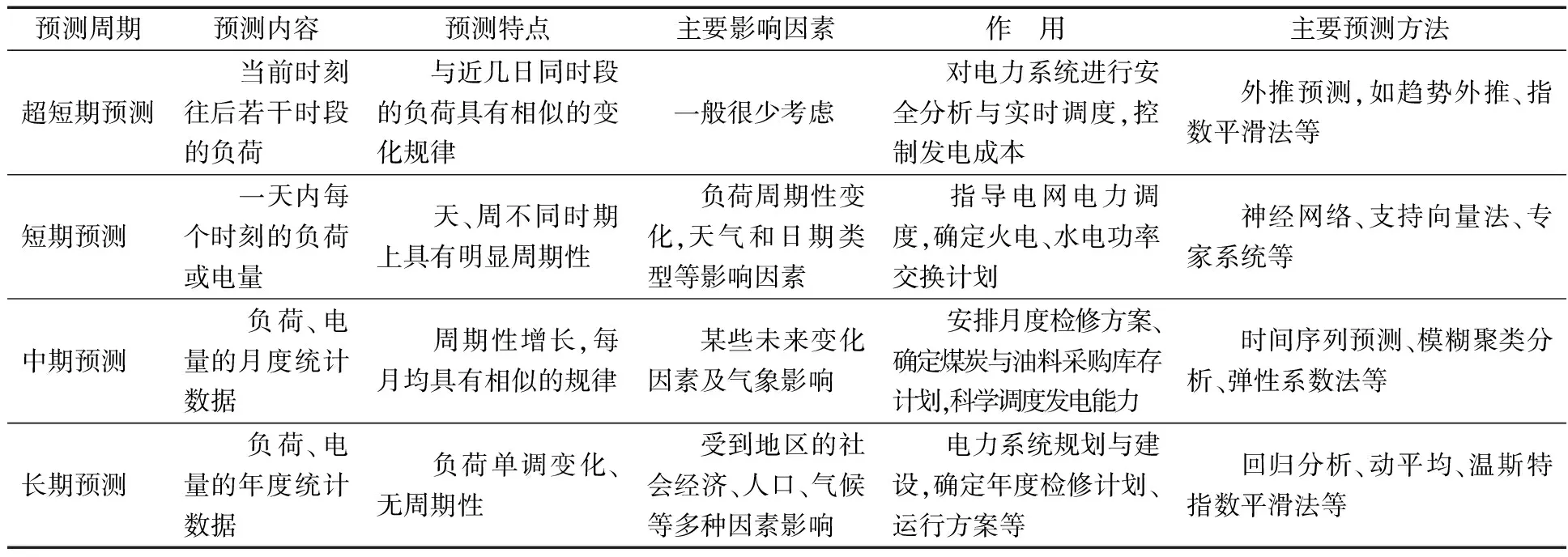
表1 不同预测周期对比
2 负荷预测基本流程
图1为短期电力负荷预测的基本流程.
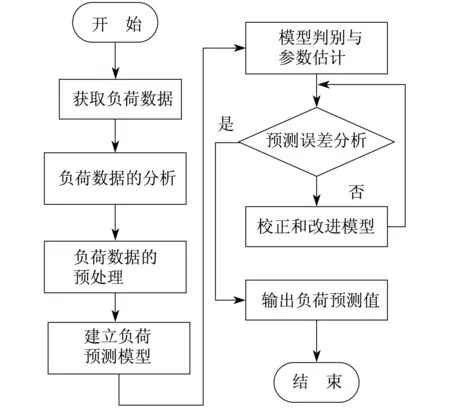
图1 短期电力负荷预测的基本流程
2.1 数据预处理
短期负荷预测是电力系统经济运行、管理调度中不可或缺的环节,其预测结果是系统安排供电、调度的基础,其准确程度决定着系统运行的安全性与经济性.但在获取的历史负荷数据中,常有一些异常数据,从而导致预测精度有所降低.如表2引用文献[13]中的Table9来表明不良数据对短期负荷预测的影响.由表2可知,对于任意不含有异常值的一组数据而言,无论采用哪种方法进行预测,其拟合误差和预测误差均最小.而当一组数据中不良值的个数变多时,其拟合误差和预测误差均会变大,如传统的带外生变量自回归滑动(Autoregressive Moving Average with Exogenous Rariables,ARMAX)模型,其拟合误差(10.56%~21.23%)与原来的(2.46%)相比增大较多.而鲁棒性强的负荷预测方法,如带外生变量模糊自回归滑动平均(Fuzzy Autoregressive Moving Average with Exogenous Input Variables,FARMAX)模型,即使对不同数量的异常数据的所有情况具有相同ARMAX(2,1,1)的结构模型时,也能够在一定范围内改善异常值的不良影响,但其拟合误差和预测误差仍会随不良数据个数的增多而变大.在所有的测试情况下,FARMAX模型的平均预测误差从1.98%(没有坏数据)增加到最大为3.66%.因此,必须减少由异常值所带来的不良影响.

表2 异常数据对拟合和预测误差的影响
针对数据异常的不同原因可以采用如下6种数据处理方法[14]:
(1) 曲线置换法 对曲线有着明显异常的或有特殊情况的日负荷量删除或者用正常曲线替换;
(2) 数据水平处理法 将负荷的某一时刻数据与其相邻时刻进行比较,若相差过大,则进行修正.
(3) 数据垂直处理法 将负荷的某时刻数据与其相邻日同一时刻进行比较,若相差过大,则用平均值替换;
(4) 经验修正法 有丰富经验的学者对比正常负荷曲线,从而对某个时段内的异常值进行修正;
(5) 分时段设定阈值法 给不同时段的负荷数据设定阈值,接着对不同区间内的各负荷值进行筛选,筛选出来的坏数据可用数据水平处理法、数据垂直处理法和概率统计法进行处理;
(6) 概率统计法 先用经验修正法筛选、处理畸变数据,再用置信区间识别、修正剩下的畸变值.
2.2 相关因素影响
在短期电力负荷预测中,常见的影响因素是温度[15],它一般由中央气象台气象指数预报可知.此外,还有如平时、周末及节假日[16]等外部因素均需考虑在内.但是由于各项特征量的量纲不相同,直接将其输入会造成误差偏大,因此需要将不同的量纲值[7]进行归一化处理,使各项特征量之间具有可比性,由此建立了指标映射数据库,如表3所示.该数据库简化了建模过程,提高了预测精度.

表3 指标映射数据库
此外,预测中还可以结合弹性电价[18]、市场环境[19]等对预测具有重要影响因素,但考虑到负荷预测受多因素共同影响,因此在研究时应通过学习方法找出影响预测精度的主要因素,并建立相关模型.
2.3 改进的T-S模糊神经网络算法
2.3.1 PSO算法
PSO算法是由KENNEDY J和EBERHART R于1995年提出的一种全局优化进化算法[20],它来自于对鸟群捕食行为的模拟和研究.假设有一群鸟正在随机搜索食物,并且只有一块食物在这个区域里,但它们只知道当前的位置距离食物有多远,却不知道食物的位置.这样,它们就可以通过当前所搜索的局部最优值来寻找全局最优值.
每个粒子均有自己的速度向量和位置向量,但在找到最优解之前,粒子会根据如下方程不断更新速度和位置:
(1)
(2)

2.3.2 基于PSO改进T-S模糊神经网络算法
PSO改进T-S模糊神经网络算法[21],即通过粒子群对模糊系统进行寻优,使学习率和平滑因子在稳定的参数间隔内动态调节,再结合局部和全局最优模糊匹配,并利用文献[22]中的公式得到惯性权重w,最后解模糊化达到目的.
(3)
(4)
(5)
其中:

(6)
式中:α——学习率[25],α∈(0,∞);θ——平滑因子,θ∈(0,1);N——第N次训练;E——误差函数;yd,yc——输出的期望值和实际值;L——训练样本的数目.
(7)
(10)
式中:m——误差足够小时的训练次数.
则:
(11)
定理如果数列{xn}收敛,当{yn}<{xn}时,则任何数列{yn}收敛,α的稳定区域为:
(12)
(13)
为了防止PSO进入局部最优化,使α和θ做如下逐渐增加:
αk+1=1.2αk
(14)
θk+1=1.15θk
(15)
式中:α0=0.001;θ0=0.001.
改进的T-S模糊神经网络算法步骤如下:
(1) 初始化 参数和权值初始化;
(2) 建模 基于PSO建立改进的T-S模型,计算输出误差和训练误差;
(3) 更新 根据公式更新相应的参数、权值、速度及位置;
(4) 判断 若PSO模型达到迭代次数最大值时,则停止迭代,并将获取的最优解带入改进的T-S模型计算输出,否则转到步骤(3);
(5) 检验 若改进的T-S模型输出最大时,迭代次数达到最大或者误差达到阈值,则停止迭代,否则转到步骤(2).
3 预测方法误差评价指标
所谓误差就是预测得出的负荷与我们所搜集到的实际负荷之间的差值,虽然负荷变化有一定的规律可循,但同样也变化莫测,这是因为并不是每个影响因素都能预知,比如自然灾害等突发情况;即使能够预知(如气象),也存在很大的随机性和不确定性,并且在建立模型的过程中也不是完全的精确.
一般常用的误差评价指标[26]如下.
(1) 平均绝对误差(MAE) 避免预测误差的正负相抵消:
(16)

(2) 均方误差(MSE) 避免正负误差不能相加的问题:
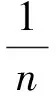
(17)
(3) 均方跟误差(RMSE) 能够很好地反映出预测的精密度:
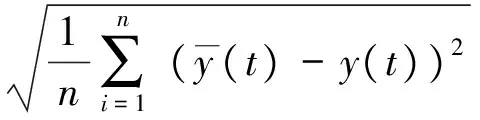
(18)
4 短期负荷预测面临的挑战
4.1 组合预测
由于单一的预测方法还存在局限性,精度还不够高,因此已有很多学者开始研究组合预测方法[27-28].
(1) 从预测机理来看,将单一预测方法组合是比较常见的方法,如KPCA和BP结合[29],模糊聚类与马尔可夫链结合[30],改进的PSO与SVM结合[31]等;
(2) 从加权组合来看,对每个预测方法赋予不同的权重[32],综合考虑得到一个最佳效果的预测模型,但如何合理地分配权重,这一问题还需作进一步研究.
4.2 自适应预测策略
部分预测方法可以根据实际情况,自动调节模型参数,如同自动控制原理的闭环思想一样,不断修正偏差、减少偏差,从而达到高精度预测,如模拟退火[33]、基于知识的专家系统[34]以及自适应加权最小二乘支持向量机[35]等.
4.3 电力负荷的预测误差
负荷历史数据的规律性在一定范围内限制了精度所能达到的最佳表现效果,因此不能随意对任何数据提出无限制的高精度的预测要求.文献[36]所提出的内蕴误差评价负荷预测方法表明了所获历史数据的客观规律性、预测方法和预测误差之间的关系,为正确评价负荷预测方法的性能、确定并可实现的负荷预测精度[37]要求提供了科学的依据,也有利于实现对预测过程的有效监视,同时也改善了预测精度.
5 结 语
本文分析了PSO改进的T-S模糊神经网络负荷预测方法.该方法在预测领域中获得了骄人的成绩.同时,在未来的负荷预测中,尽可能加大数据的挖掘力度,结合外部影响因素,以探索出更高精度的新方法.
[1] 莫维仁,孙宏斌,张伯明.面向电力市场的短期负荷预测系统设计及实现[J].电力系统自动化,2001,25(23):41-44.
[2] HOBBS B F,HELMAN U,JITPRAPAIKULSARN S,Artificial neural networks for short-term energy forecasting:accuracy and economic value[J].Neurocomputing,1998,23(1-3):71-84.
[3] 王芳芳.负荷预测模型的建立及基于回归分析法的负荷预测[J].中国高新技术企业,2011(34):56-58.
[4] 唐俊杰,牛焕娜,杨明皓.基于线性相关分析的周期自回归短期负荷预测[J].电力系统保护与控制,2010,38(14):128-133.
[5] 田德胜,刘厚法.指数平滑法在短期负荷预测中的应用[J].农村电气化,2005(2):36-37.
[6] 李艳红.基于时间序列的短期电力负荷预测模型研究[D].昆明:昆明理工大学,2011.
[7] 万志宏.基于时间序列的电力系统短期负荷预测研究[D].广州:华南理工大学,2012.
[8] WANG D,SUN Z.Big data analysis and parallel load forecasting of electric power user side[J].Zhongguo Dianji Gongcheng Xuebao,2015,35(3):527-537.
[9] WANG B,ZHAO S,ZHANG S.A distributed load forecasting algorithm based on cloud computing and extreme learning machine[J].Power System Technology,2014,38(2):526-531.
[10] YAN Z,LI D,YAO L,etal.Short-term power load forecasting based on improved T-S fuzzy-neural network[C]//World Congress on Intelligent Control and Automation,2016:109-113.
[11] TAKAGI T,SUGENO M.Fuzzy Identification of systems and its applications to modeling and control[J].Readings in Fuzzy Sets for Intelligent Systems,1993,15(1):387-403.
[12] 宋玲芳.基于模糊聚类分析与BP网络的电力系统短期负荷预测[D].西安:西安理工大学,2005.
[13] YANG H T,HUANG C M.A new short-term load forecasting approach using self-organizing fuzzy ARMAX models[J].IEEE Transactions on Power Systems,1998,13(1):217-225.
[14] 王乐.基于灰色理论和神经网络的电力系统短期负荷预测研究及其比较[D].南宁:广西大学,2012.
[15] NAHID-Al-MASOOD,SADI M Z,DEEBA S R,etal.Analyzing the impact of temperature on electrical load[C]//2010 4th International Power Engineering and Optimization Conference (PEOCO),2010:238-243.
[16] 贺蓉,曾刚,姚建刚,等.天气敏感型神经网络在地区电网短期负荷预测中的应用[J].电力系统自动化,2001,25(17):32-35.
[17] 康重庆,程旭.一种规范化的处理相关因素的短期负荷预测新策略[J].电力系统自动化,1999,23(18):32-35.
[18] 刘玉娇,蒋传文.考虑负荷周期性和变化率的短期电价预测[J].电机与控制学报,2010,14(6):21-26.
[19] 张芳明.电力市场环境下的电力系统扩展短期负荷预测研究[D].长沙:湖南大学,2009.
[20] KENNEDY J,EBERHART R.Particle swarm optimization[C]//IEEE International Conference on Neural Networks,Proceedings.IEEE Xplore,1995:1 942-1 948.
[21] 吴科,李伟华.扩展T-S模糊模型的PSO神经网络优化算法[J].计算机工程与应用,2010,46(35):238-241.
[22] CHATTERJEEA,SIARRYP.Nonlinear inertiaweight variation for dy-namic adaptation in particle swarm optimization[J].Computersand Operations Research,2006,33(3):859-871.
[23] CAMPOLUCCI P,UNCINI A.On-line learning algorithms for locally recur-rent neural networks[J].IEEE Transactions on Neural Networks and Learning Systems,1999,10(2):253-271,
[24] RAFAEL S,PIRES A J,COSTA BRANCO P J.An adaptive learning rate approach for an on-line neuro-fuzzy speed controller applied to a switched reluctance machine[C]//IEEE International Symposium on Industrial Electronics.IEEE Xplore,2005:941-944.
[25] CHADLI M,MAGUIN D,RAGOT J.Relaxed stability conditions for Takagi-Sugeno fuzzy systems[C]//IEEE International Conference on Systems,Man,and Cybernetics.IEEE Xplore,2000:3 514-3 519.
[26] 吕毅.基于改进BP算法的电力系统短期负荷预测[D].保定:华北电力大学,2007.
[27] 黄伟.短期电力负荷组合预测模型的研究[D].大连:大连理工大学,2009.
[28] 王白玲.电力负荷组合预测的理论方法及影响因素分析[D].北京:华北电力大学,2005.
[29] 刘畅,刘天琪,陈振寰,等.基于KPCA和BP神经网络的短期负荷预测[J].电测与仪表,2016,53(10):57-61.
[30] 任雪梅,陈逊,徐腊元.基于马尔可夫链和模糊聚类的电力系统短期负荷预测[J].北京理工大学学报,2004,24(5):416-418.
[31] 王义军,李殿文,高超,等.基于改进的PSO-SVM的短期电力负荷预测[J].电测与仪表,2015,52(3):22-25.
[32] 邓灿新.电力负荷组合预测模型权重算法设计与应用[J].广东电力,2012,25(6):73-76.
[33] 陈朴.模拟退火支持向量机算法研究及在电力负荷预测中的应用[D].哈尔滨:哈尔滨工业大学,2006.
[34] 刘东,李莉.小波神经网络嵌入专家系统的短期电力负荷预测[J].陕西电力,2009,37(10):44-48.
[35] 赵超,戴坤成.基于自适应加权最小二乘支持向量机的短期电力负荷预测[J].信息与控制,2015,44(5):634-640.
[36] 穆钢,侯凯元,杨右虹,等.负荷预报中负荷规律性评价方法的研究[J].中国电机工程学报,2001,21(10):96-101.
[37] 郭华安,加玛力汗·库马什,常喜强,等.电力系统短期负荷预测方法与预测精度综述[J].电气技术,2011(10):20-23.
(编辑 胡小萍)
ReviewofShort-TermPowerLoadForecastingBasedonPSOImprovedT-SFuzzy-NeuralNetwork
SHENJuan1,LIUDaming2
(a.SchoolofAutomationEngineering,b.SchoolofComputerScienceandTechnology,ShanghaiUniversityof
ElectricPower,Shanghai200090,China)
Accurate power load forecasting is beneficial to ensure the safety,stability,efficiency and economy of grid operation.In order to improve the prediction accuracy,a PSO improved T-S (Takagi-Sugeno) fuzzy neural network method is applied.The importance of data preprocessing to improving the input is analyzed and an improved T-S fuzzy neural network algorithm that can make the learning rate and smoothing factor adjust dynamically is discussed.Therefore,it can make PSO find the optimal parameters.And then,combined with historical load data and related influencing factors,it is concluded that the improved T-S fuzzy neural network has higher control precision in short-term power load.
prediction accuracy; PSO-improved T-S algorithm; fuzzy model; abnormal data
10.3969/j.issn.1006-4729.2017.04.004
2017-03-09
沈娟(1991-),女,在读硕士,安徽宣城人.主要研究方向为电力负荷预测.E-mail:shenjuan1006@126.com.
大型电气传动系统与装备技术国家重点实验室开放基金课题(SKLLDJ032016021).
TP183;TP715.1
A
1006-4729(2017)04-0325-06

