投资活动中风险偏好的度量与研究

杨雁雁

（武夷学院 数学与计算机学院，福建 武夷山 354300）

投资活动中风险偏好的度量与研究

杨雁雁

（武夷学院 数学与计算机学院，福建 武夷山 354300）

投资者的活动离不开人的主观感受与对风险的偏好，本文首先从冯诺依曼的可测效用公理出发，引用期望效应函数来描述有风险偏好的投资人的投资效用，并从定常风险和非定常风险偏好的角度给出期望效用函数计算方法与风险偏好的度量.其次从风险价值度角度，利用不同风险偏好者对风险与收益关注度的不同，给出了VAR(CVAR)模型下的风险偏好度量.最后由投资心理和偏好心理的复杂性，通过预设风险偏好性质来度量风险偏好，以增加灵活性与实用性.

期望效用；风险偏好；VAR理论；预设风险偏好性质

1 引言

随着中国金融业的发展，投资人在追求利润最大化的同时，不可避免要考虑风险因素.对相同的经济结果，投资者看重的是相对结果而不是绝对结果[1].在做决策时，必然在考虑收益的同时也要考虑风险损失，即收益与损失的联合效用.风险偏好者实施冒险的经济行为，风险规避者施行保守的经济决策.如何衡量这种风险偏好，使投资者在一定风险偏好下做出最理性决策是研究者需要研究的.

风险偏好的度量很重要，只有充分度量投资者的风险偏好，金融机构才能根据投资者的风险偏好设计相应的理财产品，增加理财产品的销量；实业公司才可以根据自己的风险偏好确定与其相一致的经营策略，实现经济运营效用最大化；投资者才可以根据自己的风险偏好，通过效用函数的构建，对自己的经济行为及时预警，防止不利经济决策的出现.然而现有研究对风险偏好的度量尚无系统化的阐述，即使在涉及投资问题时提及风险偏好，也仅作为条件判断的切入点，缺乏模型化的描述.本文从主流的研究投资活动的理论出发，对风险偏好进行度量和研究.研究投资活动的主流方法有马克维茨的均值方差理论，冯诺依曼的期望效用函数理论和风险价值度理论.马克维茨的均值方差理论要求一定收益下风险最小，并不能有效衡量投资者风险偏好的差异性，它实际上是附加了条件的期望效用函数最大化问题.

风险偏好作为一种偏好，是投资者对投资结果中收益和风险联合效用主观满意度的选择.本文从冯诺依曼的涉及偏好的四条公理出发，引入风险偏好的概念，再根据可测效用公理引出的期望效用函数，来描述风险中性者、风险厌恶者、风险爱好者的度量问题.然而可测效用公理只给出抽象的期望效用函数概念，并没有给出具体的区分不同风险偏好的效用函数.本文从风险偏好随财富水平不变和变化两个角度来求解度量风险偏好的期望效用函数，并发现在具体的求解过程中，赌博当量的确定非常重要，本文通过一个例子来说明具体的期望效用函数的求解方法.考虑到人对当前的感受要强于对未来的感受,投资者把高于一定数值的收益不看成风险，而把低于一定数值的收益看成风险，本文从VAR(CVAR)理论出发来描述风险,通过不同风险偏好者对收益和风险的关注程度的不同，来构建相应的度量风险偏好的效用函数.最后由于投资心理和偏好心理的复杂性，通过预设偏好性质来度量风险偏好，以增加灵活性与实用性.

对于风险偏好的度量，前人已做了相应的工作.冯诺依曼-摩根斯特恩在投资活动和经济行为中给出了涉及偏好的可测效用公理[2].刘宗谦[3]等给出了期望效用存在性的证明.姜青舫[4]对定常风险效用函数的导出给出了证明.徐绪松[5]从期望效用最大化的角度研究了损失规避下的投资组合问题.许民利[6]等通过条件价值建立相应的偏好决策模型.

2 期望效用函数下的风险偏好度量

理性投资者追求的是收益最大化，然投资活动的收益伴随着风险，投资者对风险的厌恶程度直接影响其经济决策，如何衡量这种风险偏好，从而在一定风险偏好程度下作出最理性的决策，即一定风险偏好下收益最大化，是我们研究的问题.这里有两点需要明确，一是风险偏好，二是收益最大化.我们把收益与风险的联合作用对投资者主观满意度的影响称为效用，在不确定条件下我们用期望效用来描述收益与风险的联合作用.

2.1 风险偏好的定义与期望效用函数的描述

假设把投资的收益看成一种“商品”或“价值”.定义“未定价值空间”ϖ，它是由“确定价值空间”的向量x,y等形成形如L={(x,y,p)|0≤p≤1}的组和更高层次的组ϖ={(L1,L2,p)|0≤p≤1}所形成的集合.其中(x,y,p)表示取x的概率为p，取y的概率为1-p.在ϖ上定义一种偏好关系≿，满足冯诺依曼-摩根斯特恩四条公理，其具体描述如下：

公理 1 (i)x≿x；

(ii)如果 x≿y，y≿z则 x≿z；

(iii)x≿y和y≿x至少有一个成立；

公理 2 (i)x=(x,y,1)；

公理3 对于∀x,y,z∈ϖ，{p∈[0,1]|(x,y,p)≿z}和p∈[0,1]|z≿(x,y,p)}都是闭集.

公理 4 如果 x～y,∀p∈[0,1]和 z∈ϖ，(x,zp)～(y,z,p).

其中符号～表示无差异量，从偏好的角度来说，x～y表示价值相等的量，也叫赌博当量.记(x,p,y)～τ，不同风险偏好所取的τ值不同.当E(x,p,y)=τ时，称该经济活动者为风险中性者，当E(x,p,y)＜τ时，该经济活动者为风险追求者；当E(x,p,y)＞τ时，该经济活动者为风险厌恶者.更一般的我们可以由期望效用函数描述这三种风险偏好，事实上有以下结论：如果(ϖ,≿)满足上述四条公理，则在ϖ上存在惟一的期望效用函数 u，满足：x≿y，且仅当 u(x)≥u(y),u(x,y,p)=pu(x)+(1-p)u(y).

上述结论的证明可以参考文献[3]，接下来我们通过期望效用函数来具体度量风险偏好.假设x表示发生风险事件的收益，y表示未发生风险事件的收益，p表示发生风险事件的概率，构造L={(x,y,p)|0≤p≤1}.由投资人的风险偏好决定的期望效用函数为u(x)，投资者对(x,y,p)这一风险事件所包含的风险态度可由u(px+(1-p)y)=u(x,y,p)的比较来刻画，如果有

成立，那么称该经济活动者为风险中性者；

如果有

成立，称该经济活动者为风险厌恶者；如果有

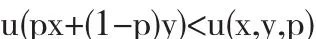
成立，称该经济活动者为风险爱好者.

2.2 风险偏好的期望效用函数度量

当财富水平的变化不改变风险偏好时，即满足(x,p,y)～τ⇔(x,p,y)+ω～τ+ω时，我们称其为定常风险偏好，对上式两端同时带入期望效用函数中运算可得

若u(x)在R上不恒为零、严格单调且连续可微，则按加法定理可以证明，当投资者为风险中性时，投资者的效用函数为u(x)=bx+d，当投资者为风险偏好或风险厌恶时，其期望效用函数u(x)=(ebcx-1)/c+d.具体的证明可以详见文献[4].

对u(x)取二阶导数，可得u(x)"=b2cebcx，当c＞0时，此时u(x)"＞0，对应的投资者为风险厌恶者，其风险厌恶程度-bc.当c＜0时，此时u(x)"＞0，对应的投资者为风险偏好者，其风险厌恶程度-bc.

假设x0表示发生风险事件的收益，y0表示未发生损失事件后的收益，发生损失时的概率为1/2，为简便起见，令u(x0)=0，u(y0)=1.假设投资者的赌博当量(x0,y0,1/2)～τ，令 z(x)=(x-x0)/(y-y0)，且 z(τ0)=1/4，联立 u(x0)=0，u(y0)=1，(x0,y0,1/2)～τ0可得其期望效用函数为u(x)=1.7841(1-e-0.8221(x-x0)/(y0-x0))，是风险厌恶的情况，其厌恶程度为0.8221/(y0-x0).

当财富水平改变风险偏好时，我们称其为非定常风险偏好，显然这在现实中更加普遍.若所取时间段很短，且在这个时间段内没有发生最严重的损失事件，可以假设财富变化对风险偏好的变化的影响不显著，我们仍然可以采用上述定常风险偏好的结论，其关键是对投资者赌博当量的测试，例如在当前财富水平下，赌博当量为(1,0,1/3)～1/2，u(x0)=0，u(y0)=1，所求得的期望效用函数是在当前财富水平下，很小时间段内的期望效用函数,对应的是风险追求的情况，其风险厌恶程度为-1.3863/(y0-x0).

3 VAR(CVAR)模型下的风险偏好度量

考虑到投资者对损失的敏感性，投资者仅把低于一定数值的收益看成风险，我们把收益区间进行分割，分为高盈利部分和低盈利部分，这里的低盈利部分就是投资者认为的风险损失部分，是投资者不希望出现的.高盈利部分是投资者认为的收益部分，是投资者所追求的.高盈利部分发生的概率为β，低盈利部分为1-β.接下来我们从CVAR模型和VAR模型来对不同风险偏好进行度量和研究.

风险规避者不仅关注自身利润，更关注风险损失情况，用CvaR衡量大于某一损失水平部分的损失期望.在给定的容忍损失水平下，风险规避者要求在这一损失水平下利润值的期望最大，即损失发生时其利润部分的期望值最大.给定某一置信水平β，β∈(0,1)，π表示收益情况，

其中Z1-β是概率为1-β时对应的分位数.CvaR为利润水平低于VaR的利润期望，则

当投资者为风险规避者时，其更关注风险损失部分的收益，目标函数为max{CvaRβπ}.当投资者为风险偏好者时，风险偏好者更关注高盈利部分的收益，即在β置信水平上，风险偏好者要求利润值不低于Z1-β的收益期望最大.风险偏好投资者的决策模型为：

不同风险偏好者对高收益部分与低收益部分关注程度也不同.为了准确度量风险偏好，假设高收益部分的占比为λ，收益期望记为E1，低收益部分占比为(1-λ)，收益期望记为E2.假设收益的密度函数为f(x)，则

风险偏好可以通过函数λE1(1-λ)E2来度量，当λ=1/2时，表示对风险和收益持相同的关注度，为风险中性.当λ＞1/2时，表示更关注收益部分，为风险追求者，且λ越大其风险厌恶程度越低.当λ＜1/2时，表示更关注风险损失部分，为风险厌恶者，且λ越小其风险厌恶程度越高.

4 设定偏好性质的风险偏好度量

除了从期望效用函数和风险价值度的角度来度量风险偏好，投资者还可以根据实际情况设定风险偏好的性质来度量风险偏好.假设投资者更加关注安全性和期望收益，设As是投资者能容忍的收益底线，从投资者的心理感受出发，用变量的实际值小于As来表示风险，即X≤As，当X＞As时表示资金安全，未来收益不低于As的概率为Ps，用p来衡量对安全性指标的重视程度.则投资者的风险偏好可以由效用函数u(x)=PSpE(x)(1-p)来度量.p值越大表明越重视安全性.

设收益X对应的概率密度函数为f(x)，则有

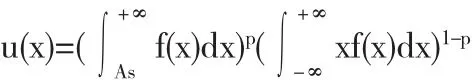
其中As与p由投资者的偏好性质预先设定.在这种风险偏好度量方法中，投资者根据历史数据得出收益的分布情况，并求出收益的概率密度函数，As是投资者容忍的收益底线，p值的确定可以由投资者过往的投资决策结合当下的风险偏好情况得出，主观性强.

类似的，在预设风险偏好性质的度量中，投资者可以根据自己的风险厌恶程度，通过预设δ值调整收益率来度量风险，δ表示对风险重视程度.如果投资者对风险厌恶程度重，则设置δ＜1,反之，对债券的长期价值比较乐观，为减少对风险的敏感度，则设置δ＜1.通过风险偏好的不同而调整的收益率z可以表示成如下形式:

a表示投资者平均收益率，X为实际收益率，ε表示决策者对收益率波动误差的估计，在实践中一般假设ε服从正态分布.δ取值大小由投资者的风险偏好程度预先设定，b的设置是为了确保δ的取值关注的是风险造成的损失，而不会同时放大收益，造成误判.

在设定风险偏好性质的风险偏好度量中，参数的选取完全由投资者的风险厌恶程度决定，且度量风险偏好的效用函数不是唯一的，它由投资者的实际需要和风险偏好的性质共同决定.与期望效用函数和条件在险价值法度量风险偏好的方法相比更加灵活且操作性更强，但由于其主观性更强且误差更大，在不需要对风险偏好精确度量的情况下可以作为度量风险偏好的重要补充.

〔1〕贺书婕.风险量化工具的决策价值[J].观察思考，2016（05）.

〔2〕von Neumann JO Morgenstern.Theory of games and economic behavior[M].Princeton,N J:Princeton University Press,1947.

〔3〕刘宗谦，付卫强，冯素芬.期望效用函数存在定理的另一种证明[J].首都师范大学学报，2008（04）.

〔4〕姜青舫.一种随机特殊函数方程的解法及定常风险厌恶效用函数的导出[J].贵州科学,1998,16(4):261-265.

〔5〕徐绪松,马莉莉,陈彦斌.考虑损失规避的期望效用投资组合模型[J].中国管理科学,2007（10）.

〔6〕许民利，聂晓哲，简惠云.不同风险偏好下双渠道供应链定价决策[J].控制与决策，2016（01）.

〔7〕史树中.金融经济学十讲[M].上海：上海人民出版社，2011.131-132.

〔8〕Jorion P(菲利普.乔瑞).风险价值 VaR[M].中信出版社，2005.400.

〔9〕李平，黄光东，路阳.基于Copula理论的多心理账户组合VaR模型与基金风险管理[J].系统工程理论与实践，2011（05）.

O29

A

1673-260X（2017）09-0003-03

2017-06-11